Transformations ppt
- 2. To transform something is to change. The main transformations include: •Translation •Rotation •Reflection •Dilatation (Enlargement)
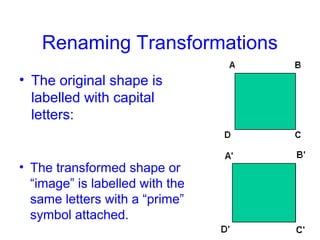
- 3. Renaming Transformations • The original shape is labelled with capital letters: • The transformed shape or “image” is labelled with the same letters with a “prime” symbol attached.
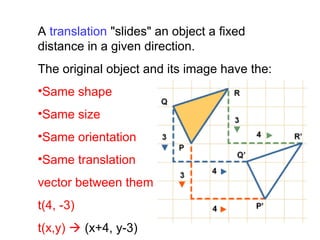
- 4. A translation "slides" an object a fixed distance in a given direction. The original object and its image have the: •Same shape •Same size •Same orientation •Same translation vector between them t(4, -3) t(x,y) (x+4, y-3)
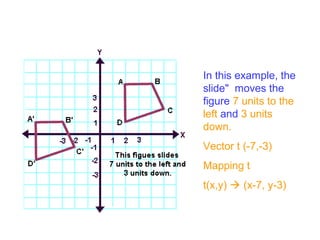
- 5. In this example, the slide" moves the figure 7 units to the left and 3 units down. Vector t (-7,-3) Mapping t t(x,y) (x-7, y-3)
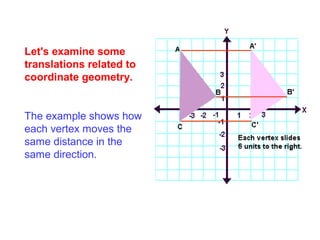
- 6. Let's examine some translations related to coordinate geometry. The example shows how each vertex moves the same distance in the same direction.
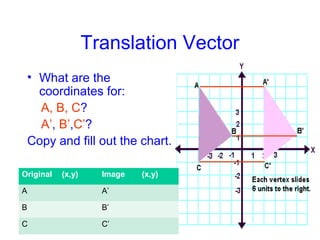
- 7. Translation Vector • What are the coordinates for: A, B, C? A’, B’,C’? Copy and fill out the chart. Original (x,y) Image (x,y) A A’ B B’ C C’
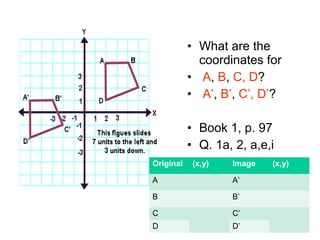
- 8. • What are the coordinates for • A, B, C, D? • A’, B’, C’, D’? • Book 1, p. 97 • Q. 1a, 2, a,e,i Original (x,y) Image (x,y) A A’ B B’ C C’ D D’
- 9. Rotations and Art The concept of rotations can be seen in wallpaper designs, fabrics, and art work.
- 10. ROTATION A rotation is a transformation that turns a figure about a fixed point. It is described in terms of: •The centre of rotation, •The direction of rotation: cw (-) or ccw (+) •The degrees of rotation An original shape and its rotation image have the: •Same size •Same shape, •Same orientation
- 11. Rotation Rules
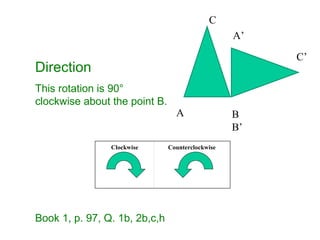
- 12. Direction This rotation is 90° clockwise about the point B. Book 1, p. 97, Q. 1b, 2b,c,h Clockwise Counterclockwise A B B’ C C’ A’
- 13. REFLECTION A reflection is described by the line of reflection. An object and its reflection have the: •Same shape •Same size •Opposite orientation
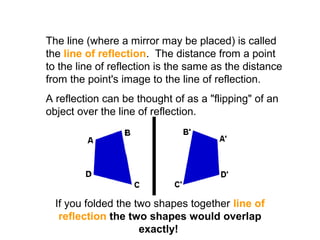
- 14. The line (where a mirror may be placed) is called the line of reflection. The distance from a point to the line of reflection is the same as the distance from the point's image to the line of reflection. A reflection can be thought of as a "flipping" of an object over the line of reflection. If you folded the two shapes together line of reflection the two shapes would overlap exactly!
- 15. What happens to points in a Reflection? • Name the points of the original triangle. • Name the points of the reflected triangle. • What is the line of reflection? • How did the points change from the original to the reflection?
- 16. Reflection Rules Page, 97, Q. 1c, 2d, f, g
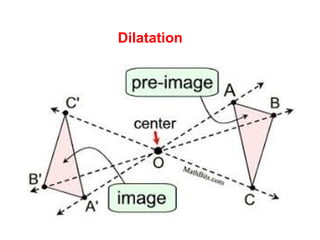
- 17. DILATATION A dilatation is a transformation that produces an image that has the •Same shape •Same orientation •Different size. •A centre of Dilatation •A scale factor A dilatation used to create an image larger than the original is called an enlargement. A dilatation used to create an image smaller than the original is called a reduction.
- 18. Dilatation
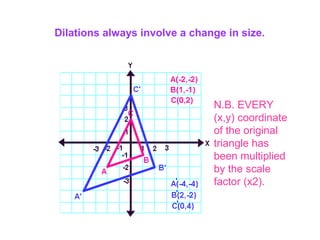
- 19. Dilations always involve a change in size. N.B. EVERY (x,y) coordinate of the original triangle has been multiplied by the scale factor (x2).
- 20. Dilatation Rules • Given an enlargement with a scale factor S, and the center of dilatation at the origin, • (x,y) (Sx, Sy) • E.g. Centre at (0,0), Scale Factor 2 • (x,y) (2x, 2y) • (3,4) (2x3, 2x4) = (6,8) • Page 109, Q. 1a, c, f
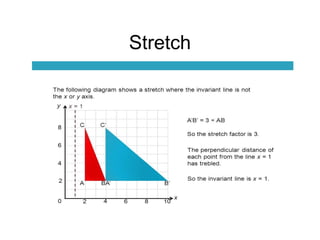
- 21. Stretch Rules • A stretch is a dilatation in which only one of the coordinates is affected. • E.g. the x value is stretched by a factor of 2 • (x,y) (2x, y) • (5,8) (10, 8) • E.g. the y value is compressed by a factor of 4 • (x,y) (x, y/4) • (5,8) (5, 2) Page 111, Q. 5 a,b,c
- 22. Stretch
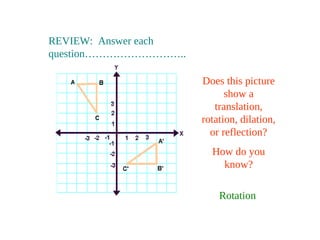
- 23. REVIEW: Answer each question……………………….. Does this picture show a translation, rotation, dilation, or reflection? How do you know? Rotation
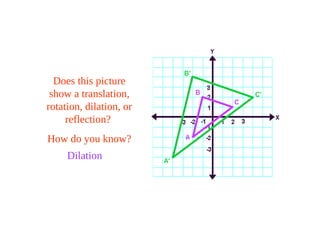
- 24. Does this picture show a translation, rotation, dilation, or reflection? How do you know? Dilation
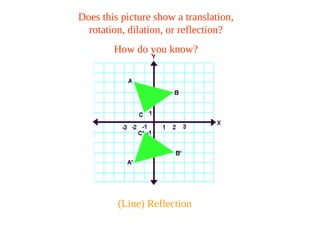
- 25. Does this picture show a translation, rotation, dilation, or reflection? How do you know? (Line) Reflection
- 26. Which of the following lettered figures are translations of the shape of the purple arrow? Name ALL that apply. Explain your thinking. Letters a, c, and e are translations of the purple arrow.
- 27. Has each picture been rotated in a clockwise or counter-clockwise direction? The birds were rotated clockwise and the fish counterclockwise.
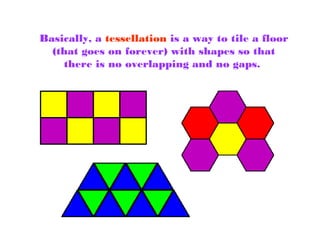
- 28. Basically, a tessellation is a way to tile a floor (that goes on forever) with shapes so that there is no overlapping and no gaps.
- 29. Dutch graphic artist M. C. Escher (1898-1972) is known for his creative use of tessellations in his work. What transformations can you see in this picture? The birds and fish have been translated here.
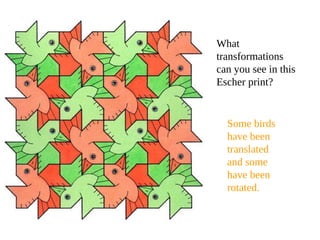
- 30. What transformations can you see in this Escher print? Some birds have been translated and some have been rotated.
- 31. Can you name examples in real life of each transformation? •Translation •Rotation •Reflection •Dilation
- 32. Check out these sites: http://www.farraguttn.com/fhs/math/nctm/index.htm http://www.mathsnet.net/transformations/index.html http://www.mcescher.com/