Belajar merupakan salah satu kebutuhan manusia . Tanpa disadari, masa kecil kita dimulai dengan belajar. Banyak sekali ilmu yang dapat kita pelajari dengan cara yang menyenangkan dan itu menuai beragam manfaat hingga kita dewasa. Begitupun dengan matematika, materi integral adalah salah satu konsep penting dalam matematika yang memiliki beragam aplikasi di berbagai bidang, termasuk fisika, ekonomi, dan ilmu komputer.
Kini mari kita menjelajahi pengertian integral, rumus dasarnya, dan sifat-sifat integral yang terkait dengan konsep ini. Dengan pemahaman yang baik tentang integral, kita dapat memanfaatkannya secara efektif untuk memecahkan masalah yang melibatkan luas, volume, dan banyak aplikasi matematika lainnya. Mari kita mulai dengan pemahaman dasar tentang materi integral.
Cek di sini untuk kursus matematika terbaik
Pengertian Integral
Integral adalah salah satu konsep utama dalam kalkulus, yang digunakan untuk menghitung luas daerah tertentu di bawah kurva fungsi. Integral juga dapat dianggap sebagai "kebalikan" dari operasi diferensial sehingga disebut juga sebagai "anti turunan" . Secara sederhana, bentuk penjumlahan kontinu yang terdiri dari anti turunan disebut dengan "integral". Berdasarkan pengertian tersebut ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral. Pertama, integral sebagai invers / kebalikan dari turunan integral disebut sebagai Integral Tak Tentu. Kedua, integral sebagai limit dari jumlah atau suatu luas daerah tertentu disebut integral tentu.
Integral tak tentu tidak hanya diaplikasikan dalam matematika, ini juga banyak digunakan dalam ilmu fisika. Umumnya, konsep integral tak tentu berguna dalam ilmu fisika untuk menghitung jarak kecepatan percepatan, mengetahui f(x) jika f’(x) dan f(a) diketahui, dan mengetahui f(x) jika gradien garis singgung dan titik singgung diketahui.
Integral merupakan bagian dari ilmu matematika yang memiliki banyak manfaat untuk kehidupan, selain perhitungan matematika untuk mengukur kuas bidang, menghitung volume benda putar, maupun menentukan panjang busur. Salah satu contoh penerapan integral matematika adalah digunakan untuk membuat desain pesawat terbang, mengetahui fungsi produksi dan konsep elastisitas dalam ilmu ekonomi, serta perancangan pembangunan gedung pencakar langit yang menggunakan ilmu integral matemaika agar tidak roboh diterpa angin. Dapatkah Anda menemukan penerapan konsep integral lainnya? Tuliskan pada kolom komentar!
Pelajari juga pengertian bilangan rasional untuk menambah pengetahuan Anda!
Rumus Dasar Integral
Untuk menghitung integral matematika, kita menggunakan rumus dasar integral yang dikenal sebagai "rumus integral". Rumus ini digunakan untuk menentukan fungsi antiderivatif dari fungsi yang diberikan. Fungsi antiderivatif ini dikenal sebagai fungsi primitif atau integral tak tentu. Simbol yang digunakan untuk integral tak tentu adalah ∫ (integral) diikuti oleh fungsi yang akan diintegralkan dan simbol diferensial dx yang menunjukkan variabel integrasi.
Misalnya, rumus integral dasar untuk menghitung integral dari suatu fungsi f(x) adalah:
∫ f(x) dx = F(x) + C
Di sini, F(x) adalah fungsi antiderivatif dari f(x), dan C adalah konstanta integrasi. Konstanta integrasi ditambahkan karena antiderivatif dari suatu fungsi tidak unik dan dapat berbeda dengan konstanta yang berbeda
Ikuti tulisan Kami lainnya untuk memahami cara pembagian polinomial dalam Matematika!
Integral Tak Tentu
Integral tak tentu adalah proses pengintegrasian fungsi yang hasilnya berupa fungsi baru dengan konstanta tambahan yang disebut sebagai konstanta integrasi (biasanya dilambangkan dengan 
). Berbeda dengan integral tentu yang memiliki batas atas dan bawah, integral tak tentu tidak dibatasi oleh nilai tertentu dan menghasilkan keluarga fungsi sebagai jawabannya.
Secara matematis, integral tak tentu dari suatu fungsi 
dinyatakan sebagai:
Di mana 
adalah hasil integral dari , dan adalah konstanta integrasi. Penting untuk memahami bahwa integral tak tentu menghitung anti-turunan dari fungsi , yaitu fungsi yang bila diturunkan kembali akan menghasilkan .
Aturan Integral Tak Tentu
Untuk menghitung integral tak tentu dengan benar, ada beberapa aturan integral yang perlu dikuasai. Aturan-aturan ini membantu dalam menyederhanakan dan menyelesaikan berbagai jenis fungsi yang diintegralkan. Berikut adalah beberapa aturan integral dasar yang sering digunakan dalam soal integral tak tentu:
1. Aturan Konstanta: Jika ada konstanta 
, maka:
2. Aturan Pangkat (untuk 
):
Ini adalah salah satu aturan perkalian integral yang paling sering digunakan dalam integral aljabar, terutama ketika mengintegralkan polinomial.
3. Aturan Penjumlahan dan Pengurangan:
Aturan ini membantu menyederhanakan fungsi yang merupakan penjumlahan atau pengurangan dari beberapa fungsi.
4. Aturan Perkalian Konstanta:
Di sini, adalah konstanta yang dapat dikeluarkan dari operasi integral.
Dengan menggunakan aturan-aturan ini, kamu bisa menyelesaikan berbagai jenis integral tak tentu dengan lebih mudah.
Periksa di sini untuk les matematika di Bandung
Integral Tentu
Integral tentu adalah integral yang hasil akhirnya berupa nilai numerik, bukan fungsi, karena dilakukan dalam suatu interval tertentu. Integral ini digunakan untuk menghitung area di bawah kurva atau volume benda putar yang memiliki batas jelas.
Secara matematis, integral tentu dari suatu fungsi dalam interval 
dinyatakan sebagai:
Di sini, 
adalah batas bawah integral dan 
adalah batas atasnya. Proses menghitung integral tentu melibatkan pengintegrasian fungsi terlebih dahulu, kemudian memasukkan batas atas dan batas bawah untuk mendapatkan nilai akhirnya. Ini berbeda dengan integral tak tentu yang tidak memiliki batas dan hasilnya berupa fungsi plus konstanta integrasi .
Aturan Integral Tentu
Untuk menyelesaikan soal integral tentu, penting untuk menguasai beberapa aturan integral yang akan memudahkan perhitungan. Berikut ini beberapa aturan integral yang sering digunakan dalam menyelesaikan soal integral tentu:
1. Aturan Dasar:
Jika adalah anti-turunan dari , maka integral tentu dari dalam interval adalah:
2. Aturan Penjumlahan dan Pengurangan:
Aturan ini membantu memisahkan integral dari dua fungsi yang dijumlahkan atau dikurangkan.
3. Aturan Perkalian Konstanta:
Di sini, 
adalah konstanta yang dapat dikeluarkan dari operasi integral.
Pahami juga rumus dasar deret dan baris aritmatika di tautan Kami lainnya!
Contoh Soal Integral
Pemahaman konsep integral kelas 11 tidak hanya bergantung pada teori, tetapi juga pada latihan yang intensif. Melalui latihan soal integral, anda dapat mengasah kemampuan dalam menyelesaikan berbagai jenis soal integral, termasuk integral tak tentu, integral tentudan soal-soal yang melibatkan aturan integral. Mari kita mulai dengan contoh sederhana untuk memperkuat pemahaman tentang integral tentu contoh soal:
Contoh Soal 1:
Hitunglah nilai dari:
Penyelesaian:
Langkah pertama adalah mengintegralkan fungsi 
. Menggunakan aturan pangkat dan konstanta, kita dapatkan:
Selanjutnya, kita substitusi batas atas dan batas bawah ke dalam hasil integral:
Jadi, hasilnya adalah:
Jadi, nilai integral tentu dari 
dengan batas 1 sampai 3 adalah 18.
Contoh Soal 2
Hitunglah integral berikut:
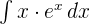
Penyelesaian:
Langkah pertama dalam metode integrasi parsial adalah memilih 
dan 
. Dalam kasus ini, kita dapat memilih 
dan 
. Dengan demikian, kita mendapatkan:
Menggunakan rumus integrasi parsial:
Karena 
, maka hasil akhirnya adalah:
Jadi, integral dari 
adalah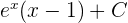 
.
Contoh Soal 3
Hitunglah nilai dari:
Penyelesaian:
Kita sudah tahu bahwa integral tak tentu dari adalah 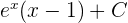. Sekarang kita terapkan batas atas dan batas bawah:
Jadi, hasil akhirnya adalah:
Nilai integral tentu dari dengan batas 0 sampai 1 adalah 1.
Contoh Soal 4:
Integralkan fungsi aljabar berikut:
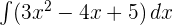
Penyelesaian:
Untuk menyelesaikan integral ini, kita terapkan aturan integral pangkat dan konstanta pada setiap suku dari fungsi tersebut:
Sehingga, hasil dari integral tersebut adalah:
Di sini, kita mengintegralkan setiap suku secara terpisah menggunakan aturan pangkat dan konstanta. Contoh ini menunjukkan cara menyelesaikan integral aljabar sederhana.
Latihan Soal Integral
Agar lebih paham, berikut beberapa latihan soal integral kelas 12 yang bisa kamu coba:
1. Latihan Soal 1:
Hitunglah integral berikut:
2. Latihan Soal 2:
Selesaikan soal berikut:
Dengan mengerjakan soal-soal ini, kamu akan terbiasa dalam menggunakan berbagai aturan integral serta memahami integral perkalian dengan lebih baik.
Jika Anda kesulitan memahami materi integral kelas 11, mencari guru privat adalah solusi yang tepat untuk membantu Anda menguasai konsep ini dengan lebih mudah. Dengan bimbingan dari seorang guru privat, Anda dapat mempelajari soal-soal integral secara mendalam, mendapatkan penjelasan yang lebih terperinci, dan latihan yang sesuai dengan kebutuhan Anda. Jangan biarkan kesulitan dalam belajar menghentikan langkah Anda! Temukan guru privat yang tepat di Superprof dan tingkatkan kemampuan Anda dalam matematika hari ini.
Pelajari juga limit fungsi Aljabar!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
