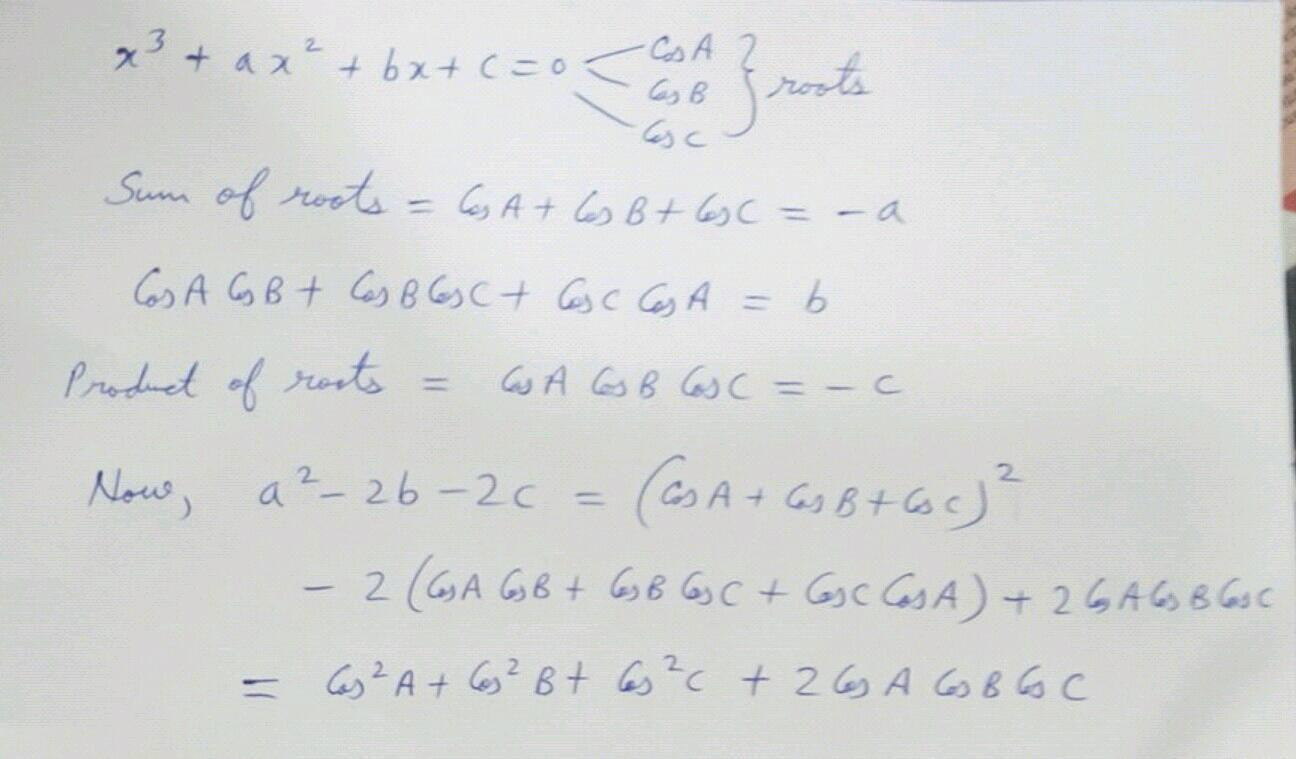Solve
Guides
0
You visited us 0 times! Enjoying our articles? Unlock Full Access!
Question

0.4 If \( \cos A , \cos B \) and \( \cos C \) are the roots of the cubic \( x ^ { 3 } + a x ^ { 2 } + b x + c = 0 \) where \( A , B , C \) are the angles of a triangle then find the value of \( a ^ { 2 } - 2 b - 2 c \)

Open in App
Solution
Verified by Toppr




Was this answer helpful?
0
Similar Questions
Q1
In a triangle ABC, if the sides a,b,c are roots of x3−11x2+38x−40=0 then find the value of cosAa+cosBb+cosCc
View Solution
Q2
If the sides a,b,c are sides of a triangle ABC are roots of the equation x3−15x2+47x−82=0 then the value of cosAa+cosBb+cosCc equal to
View Solution
Q3
If the sides a, b, c of a triangle ABC are the roots of the equation x3−13x2+54x−72=0, then the value of cos Aa+cos Bb+cos Cc is equal to
View Solution
Q4
In △ABC, if the sides a,b,c are the roots of x3−11x2+38x−40=0, then the value of cosAa+cosBb+cosCc=
View Solution
Q5
Let a, b and c be the sides of a ΔABC. If a2,b2andc2 are the roots of the equation (x3−Px2+Qx−R=0), where P, Q and R are constants then the value of

(cosAa+cosBb+cosCc) is equal to

View Solution