Preprint
Article
Hyperchaotic Maps and the Single Neuron Model: A Novel Framework for Chaos-Based Image Encryption
Altmetrics
Downloads
134
Views
44
Comments
0
This version is not peer-reviewed
Research on the Application of Digital Signal Processing
Submitted:
08 April 2023
Posted:
10 April 2023
You are already at the latest version
Alerts
Abstract
With the explosion of the generation, transmission and sharing of image data over the Internet and other unsecured networks, the need and significance for the development of novel image encryption algorithms is unprecedented. In this research work, we propose a novel framework for image encryption that is based on two hyperchaotic maps, utilized in conjunction with the single neuron model (SNM). The framework entails three successive stages, where in every stage, a substitution box (S-box) is applied, then XORing with an encryption key is carried out. The S-boxes and the encryption keys are generated from the numerical solutions of the hyperchaotic maps and the SNM. The performance of the proposed framework is gauged through a number of metrics, reflecting superior performance and complete asymmetry between the plain images and their encrypted versions. However, the main advantages of this work are: (1) The attained width of the key space; and (2) The achieved efficiency in software implementation. The superior key space of 2^{2551} is the result of employing the two hyperchaotic maps, while the improved efficiency, resulting in an average encryption rate of 8.54 Mbps, is the result of the utilization of the single neuron model, as well as the employment of optimized parallel processing techniques. In addition, the proposed encryption framework is shown to output encrypted images that pass the NIST SP 800 suite.
Keywords:
Subject: Computer Science and Mathematics - Security Systems
1. Introduction
With the widespread use of digital images in various fields, including healthcare, finance, and personal communication, there is a growing need to ensure their secure communication and storage. This is especially true in terms of protecting them from unauthorized access, tampering, and interception [1,2]. Encryption is the process of converting plaintext (unencrypted data) into ciphertext (encrypted data) using an encryption algorithm and a secret key. The encrypted data can only be decrypted and read by someone who has the correct key. Image encryption is a specific type of encryption that is designed to protect digital images, through eradicating any symmetry between a plain image and its encrypted version. The need for image encryption arises from several factors. Firstly, digital images often contain sensitive information, such as personal photos, medical images, or confidential documents. This information needs to be protected from unauthorized access or interception during transmission over the internet or storage on a device [3]. Secondly, images can be easily tampered with, and it is often difficult to detect such tampering. Encryption can help to prevent unauthorized modifications of the image data by providing a way to verify the authenticity of the image [4]. Thirdly, images are often stored and transmitted in large quantities, making it difficult to ensure the security of each individual image. Image encryption algorithms can help to secure large quantities of images by providing a way to efficiently and securely process their data [5].
Recent literature shows reliance of image encryption algorithms on substitution-permutation networks (SPNs). SPNs are a popular cryptographic primitive used in symmetric key encryption algorithms. These operate by applying a series of substitution and permutation operations to plaintext blocks, producing ciphertext blocks that are difficult for an attacker to decipher without the correct key. SPNs have been widely used in image encryption research due to their ability to efficiently encrypt large amounts of data while maintaining strong security guarantees [6,7,8,9,10]. In an image encryption algorithm, the plaintext is typically represented as a matrix of pixel values, and the SPN is applied to each pixel value individually or to a block of pixels simultaneously. One of the main advantages of using SPNs in image encryption is their ability to provide a high degree of confusion and diffusion, satisfying Shannon’s theory of secure communication [11]. Confusion refers to the property of the encryption algorithm that makes it difficult for an attacker to relate the ciphertext to the plaintext, while diffusion refers to the property that ensures that small changes in the plaintext lead to significant changes in the ciphertext [2].
SPNs have also been used in combination with other cryptographic techniques, such as key management and authentication, to provide a more comprehensive approach to image security [12]. For example, some image encryption algorithms based on SPNs use secret key management techniques to ensure that the encryption key is securely distributed and protected from unauthorized access [13]. Overall, the importance of SPNs in image encryption research lies in their ability to provide strong security guarantees while efficiently processing large amounts of data. As such, they have become a cornerstone of modern image encryption algorithms and continue to be an active area of research in the field of cryptography. In general, most recent literature on image encryption carries out confusion through the application of one or more substitution boxes (S-boxes), while diffusion is carried out through the application of an encryption key that is based on a pseudo-random number generated bit-stream, where an appropriate logical operation is utilized [7,8,14,15,16]. The next couple of paragraphs introduce each of those steps.
Substitution boxes are an important component of many image encryption algorithms. These are used to substitute plaintext bits with ciphertext bits, and they provide a key component of the confusion step in many encryption algorithms [7]. The importance of S-boxes in image encryption algorithms lies in their ability to provide strong security guarantees by introducing non-linear transformations into the encryption process. S-boxes help to ensure that changes to a single input bit have unpredictable and significant effects on the output, making it difficult for an attacker to analyze and reverse-engineer the encryption process. In image encryption, S-boxes are typically used in combination with permutation operations to form SPNs [14]. As aformentioned, the SPN structure is particularly well-suited to image encryption because it provides a high degree of confusion and diffusion, which are both important properties for secure encryption. The use of S-boxes in image encryption algorithms can also help to prevent common attacks, such as differential and linear cryptanalysis, which rely on analyzing the statistical properties of the encryption process. S-boxes can help to obscure these statistical properties, making it more difficult for an attacker to break the encryption [15].
Pseudo-random number generators (PRNGs) play an important role in image encryption algorithms. PRNGs are used to generate a sequence of random numbers that are used to encrypt the image data. These random numbers are combined with the original image data using various encryption techniques to produce encrypted image data that is difficult to decipher without the correct key [2]. The importance of PRNGs in image encryption algorithms lies in their ability to generate a large amount of unpredictable and uniformly distributed random numbers. These random numbers are crucial for achieving the two main goals of encryption: confidentiality and integrity [3]. Confidentiality refers to the property of the encryption algorithm that ensures that only authorized parties can access the encrypted data. Integrity refers to the property that ensures that the encrypted data has not been tampered with or modified during transmission or storage. PRNGs are designed to produce random numbers that are indistinguishable from true random numbers. However, unlike true random number generators, PRNGs are deterministic and rely on a seed value to produce the same sequence of numbers each time they are used with the same seed [14]. The seed value is typically generated from a source of true randomness, such as atmospheric noise, mouse movements, or keyboard timings, to ensure that the resulting sequence of numbers is sufficiently unpredictable. In image encryption algorithms, PRNGs are used to produce a large sequence of random numbers that are combined with the original image data to produce encrypted data [2]. The strength and quality of the encryption depends on the randomness and uniformity of the PRNG output. Therefore, selecting a secure and robust PRNG is essential for ensuring the security and effectiveness of the image encryption algorithm.
Chaotic functions exhibit sensitive dependence on initial conditions and cycloidal behavior, making them suitable for encryption applications [6,10]. There are two main types: low dimensional chaotic functions with 2-3 variables, and hyperchaotic functions with 4 or more variables. Low dimensional chaotic functions, like the Lorenz or Henon maps, have a smaller key space but simpler computational requirements, making them faster and easier to implement [16,17,18]. However, their lower dimensionality means they have weaker encryption strengths. Hyperchaotic functions, on the other hand, have a much larger key space due to their extra variables, providing stronger encryption. But they also have greater complexity, requiring more computing power and being slower to compute. Each type has its advantages and disadvantages for image encryption. Low dimensional chaos is suitable for real-time encryption of streaming videos or wireless communications due to its simplicity. Hyperchaos provides very high encryption strength suitable for encrypting still images or large file transmissions. However, its added complexity may be impractical for some applications with limited resources. By tuning the parameters of a chaotic map, its dynamics can be made sufficiently random-like for encryption, yet still deterministic for decryption [15]. Chaotic ciphers have been shown to withstand various attacks like brute-force, known-plaintext, and statistical analysis [14]. When combined with other techniques like diffusion and confusion layers, chaos-based encryption schemes can achieve robust and versatile encryption of images and multimedia data [19]. Chaos provides an efficient and simple means of generating the complex, nonlinear transformations needed for strong encryption.
Recent literature in the field of image encryption provides a plethora of articles that combine the use of successive applications of PRNGs and S-boxes to carry out image encryption. In many instances, chaos theory is employed to generate the PRNGs and to construct the S-boxes. In [14], the authors numerically solve the fractional-order hyperchaotic Chen system and generate a PRNG as an encryption key from its solution. They combine its use, in a multi-layer encryption algorithm, with other keys and S-boxes based on the Mersenne Twister, OpenSSL, Rule 30 cellular automata and Intel’s math kernel library. The authors of [7] make use of a tan variation of the Logistic map to carry out DNA coding as a first stage of encryption. Subsequent stages utilize the Lorenz chaotic system to construct an S-box, as well as the Logistic map in its original form for PRNG key generation. A a Recaman’s sequence in conjunction with the Rossler chaotic system are used to generate PRNG encryption keys in [20]. In [21], the authors employ chaotic functions, DNA computing, SHA-256, as well as the random movements of a chess piece, Castle, on a hypothetical chess board, to carry out image encryption. The combination of DNA coding with chaos theory is also utilized in [22], where the authors further the image encryption abilities through SHA-2. A number of dynamical functions that exhibit chaotic behavior are utilized in [19] to generate PRNG encryption keys, including the the linear congruential generator, the Arnold cat map, the Bernoulli map, the 2D logistic sine map and the tent map. In [23], parameters are computed over the finite field through the utilization of a finite field with the aim of generalizing the Logistic map and searching for an auto morphic mapping between 2 logistic maps, to carry out robust image encryption. The work of [17] adopts a continuous chaotic system, with the aim of achieving diffusion, and an LA-semi group, with the aim of achieving confusion, for efficient image encryption. A 6D discrete hyperchaotic system is employed in [24] to generate 6 PRNGs as encryption keys. Those are used conjunction with DNA coding, to encrypt each of the color-separated RGB channels of a color image. The authors of [25] make use of spatio-temporal chaos of the 2D nonlinear coupled map lattices and genetic operations, to carry out low complexity image encryption. The Mandelbrot set is utilized in a color image encryption scheme proposed in [26], where the Arnold map combined with DNA sequences enhance the attained encryption security. The authors of [27] propose an innovative image encryption algorithm that draws on the distinctive concept of a rotor machine, in addition to the employment of a piece-wise linear chaotic map and a one time key. The Logistic map is used in combination with a dynatomic modular curve, as a form of an SPN, to perform secure image encryption in [28]. In [29], the authors employ a cloud model Fibonacci chaotic system and a matrix convolution operation for to implement a secure image cryptosystem. An interesting work involving the Josephus problem, and its corresponding Josephus function, is employed in [30] in combination with a 4D hyperchaotic function. Image compression and encryption is carried out in [31], where the Arnold map and choas theory are utilized for effective and reliable image transmission over unsecured networks.
It is clear from the literature review the abundance of techniques and algorithms that may be utilized to successfully implement a secure, robust and efficient image encryption algorithm. However, almost all of the aforementioned algorithms are only able to offer 2 out those 3 vital encryption traits. Such that the offering of higher security, through more encryption stages, is counter-acted with higher design complexity and software implementations. In some cases, efficiency is capitalized on, but security is not fully achieved, such that key spaces are rather small. In order to achieve all 3 traits of security, robustness and efficiency, this work proposes and accomplishes the following:
- A chaos-based, 3-stage, dual-acting image encryption framework is proposed. In every stage, a novel S-box is constructed and applied. This is followed by the generation and application of the logical XOR operation between a generated PRNG key and the image bits.
- In the first stage, a 7D hyperchaotic system of differential equations is numerically solved and its solution is utilized both for PRNG key generation and S-box construction.
- In the second stage, a single neuron model is numerically solved and its solution is utilized both for PRNG key generation and S-box construction.
- In the third stage, a 4D hyperchaotic system of differential equations is numerically solved and its solution is utilized both for PRNG key generation and S-box construction.
- The utilization of 3 different systems, 2 of which are hyperchaotic, as well as the selection of 3 S-boxes that satisfy certain criteria, a rather wide key space of is achieved, providing sufficient resistivity to brute-force attacks.
- The software implementation of the proposed image encryption framework makes use of advanced parallel processing techniques. This allows for an average encryption rate of Mbps to be achieved.
This article is organized as follows. Section 2 makes reference to the foundational systems of differential equations that are to be employed for PRNG key generation and outlines the adopted methodology for the construction of S-boxes. Section 3 introduces the image encryption and decryption processes of the proposed framework. Section 4 provides the numerical results and performance evaluation of the proposed framework. A comparative study with the state-of-the-art is also carried out in this section. Section 5 concludes this research work and provides some suggestions for possible future areas of research.
2. Preliminary Mathematical Constructs
A number of mathematical constructs are made use of in the proposed image encryption framework to generate the PRNG keys and S-boxes. These are presented in this section.
2.1. The Single Neuron Model
The authors of [32] have shown that a single neuron model (SNM) with adapting feedback synapse has 2 coexisting chaotic attractors. In this work, we make use of this SNM because of its rich complex dynamics and its suitability to induce randomness in a simple and deterministic manner. The SNM is described as follows:
where , while p and q are positive constants. As in [32], we let (shown in Figure 1), while . The connected chaotic attractor of this system is plotted in Figure 2 for , and . In Figure 2, the colors model the time factor representing initiations with cold colors and ending with hot colors. In [32], bifurcation diagrams are provided for the SNM confirming its chaotic behavior, however a Lyapunov exponents plot is not provided, so we provide such a plot in Figure 3. It is clear from Figure 3 that 2 Lyapunov exponents materialize, where one of them is positive.
2.2. The 4D Hyperchaotic System
A 3D hyperchaotic system was proposed for the first time by the authors of [33]. This system was later on improved by the authors of [34] who added a linear controller, resulting in the following 4D system of differential equations:
where and p are the states of the system and are positive real parameters of the system and . By letting and varying k, such that , the authors of [34] show that the system in (2) possess hyperchaotic attractors and 2 positive Lyapunov exponents, providing the related plots that justify their claims (see Figure 1 for the Lyapunov exponents and Figure 2 for the bifurcation diagram, in [34]). In relation to image encryption, these properties make this system a good choice for utilization in PRNG generation and subsequent S-box construction. Furthermore, as a 4D system, the system in (2) has a large number of states and parameters, which allows it to provide an excellent expansion to the key space of the proposed image encryption algorithm.
Figure 4.
Hyperchaotic attractors for the system (2) with , shown for various 3D spaces.
Figure 4.
Hyperchaotic attractors for the system (2) with , shown for various 3D spaces.
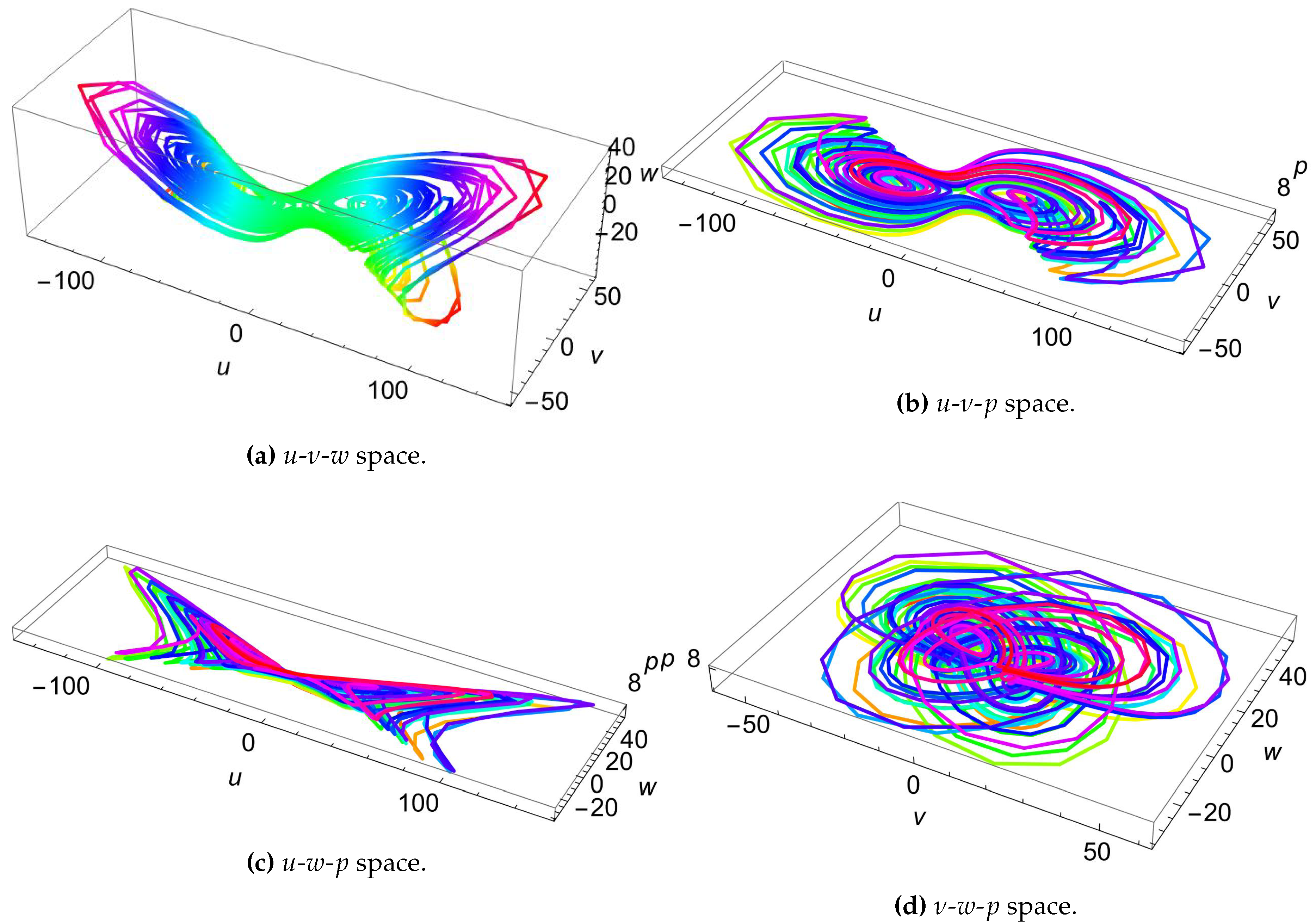
2.3. The 7D Hyperchaotic System
The authors in [35] presented a 7D hyperchaotic system. In their work, they propose coupling the classical Lorenz 3D system with a 6D hyperchaotic system. This 6D system is obtained through the addition of a nonlinear feedback controller to the first equation and a linear feedback controller to the second equation of the classical Lorenz 3D system. Such coupling results in a novel 7D hyperchaotic system as follows:
where are the states of the system and and m define its parameters. The following set of values for the parameters allow the system in (3) to have 7 Lyapunov exponents of which 5 are positive: . Figure 5 displays the hyperchaotic attractors of this 7D system. While the system in (3) is shown to have a rather simple algebraic structure, nevertheless, it exhibits complex dynamical behaviors, due to possessing 5 positive Lyapunov exponents. The authors in [35] provide the related plots that justify their claims (see Figure 6 for the Lyapunov exponents and Figure 7 for the bifurcation diagram, in [35]). In relation to image encryption, these properties make this system a good choice for utilization in PRNG generation and subsequent S-box construction. Furthermore, being a 7D system, it has a large number of states and parameters, which allows it to provide an excellent expansion to the key space of the proposed image encryption algorithm.
2.4. S-Box Construction
In this work, the main aim of the S-box construction process is to involve the S-box evaluations in the generation process. In other words, the numerical values produced by the techniques used in evaluating the performance of S-boxes are utilized as part of the key space of the S-box generation step (which is reflected on the overall key space of the proposed image encryption framework). Moreover, the process adopted here makes use of the generated PRNG bit-streams discussed in Sections 2.1–2.3. Accordingly, 2 mechanisms are applied to achieve that, with one of them being a sub-routine to the other.
Starting with the inner process, the aim is to transform a bit stream of length 2048 into an S-box. This is performed by, first, converting the 2048 bits into 256 integers. As these integers are randomly generated, they are expected to be unsorted and containing duplicates. Hence, this set of integers is utilized as a selection function applied on a sorted set , where the selected element from the set is removed. Therefore, the selected integers are re-adjusted to the length of the sorted set using the modulus operator. As a result of the selection and the re-adjustment processes being applied sequentially, values are shifted from the sorted set (which descents in size) into the S-box, generating an S-box by the time the length of the sorted set reaches 0.
Based on the inner process discussed above, the role of the outer process is to generate a set of S-boxes, evaluate each one individually, and select the S-box with performance evaluation values closest to a provided set of values. In consequence, a bit-stream of size is needed as an input, such that n is the number of S-boxes to be generated, evaluated, and one is selected from. Given such input, the bit-stream is partitioned into sections of lengths 2048, transformed into S-boxes (using the inner process), evaluated, and the performance evaluations values are subtracted from the given target evaluations yielding the S-box with the smallest difference.
3. Proposed Image Encryption Framework
The encryption process is described in Section 3.1, while the decryption process is described in Section 3.2. Section 3.3 presents algorithms that are employed as part of the encryption and decryption processes.
3.1. The Encryption Process
The following sequence of steps outline the proposed 3-stage encryption process.
- 1.
- A color image I of length M and width N is chosen and the pixel values of its RGB channels are arranged as a single bit-stream d, of length where:
- 2.
-
Encryption stage 1: The 7D hyperchaotic system encryption key and S-box.
- (a)
- The 7D hyperchaotic system is numerically solved for the S-box seeds, then the numerical solution is utilized in Algorithm 1, resulting in an S-box (shown in Table 1).
- (b)
- A replacement process is applied to the image I, employing , and resulting in image
- (c)
- The pixels of the encrypted image are transformed into a 1D bit-stream .
- (d)
- The 7D hyperchaotic system is numerically solved for the key seeds. Algorithm 2 is utilized to generate an encryption key from the obtained solution, such that the length of this key is equal to .
- (e)
- The plaintext bit-stream is XORed with the encryption key
- (f)
- The resulting bit-stream is transformed back into an image .
- 3.
-
Encryption stage 2: The single neuron model encryption key and S-box.
- (a)
- The single neuron model is numerically solved for the S-box seeds, then the numerical solution is utilized in Algorithm 1, resulting in an S-box (shown in Table 2).
- (b)
- A replacement process is applied to the image , employing , and resulting in image
- (c)
- The pixels of the encrypted image are transformed into a 1D bit-stream .
- (d)
- The single neuron model is numerically solved for the key seeds. Algorithm 2 is utilized to generate an encryption key from the obtained solution, such that the length of this key is equal to .
- (e)
- The bit-stream of the encrypted image are XORed with the encryption key
- (f)
- The resulting data bits are transformed back into an image .
- 4.
-
Encryption stage 3: The 4D hyperchaotic system encryption key and S-box.
- (a)
- The 4D hyperchaotic system is numerically solved for the S-box seeds, then the numerical solution is utilized in Algorithm 1, resulting in an S-box (shown in Table 3).
- (b)
- A replacement process is applied to the image , employing , and resulting in image
- (c)
- The pixels of the encrypted image are transformed into a 1D bit-stream .
- (d)
- The 4D hyperchaotic system is numerically solved for the key seeds. Algorithm 2 is utilized to generate an encryption key from the obtained solution, such that the length of this key is equal to .
- (e)
- The bit-stream of the encrypted image are XORed with the encryption key
- (f)
- The resulting data bits are transformed back into an image . is the final output encrypted image.
A flow chart illustrative of the proposed 3-stage encryption process is provided in Figure 6.
Figure 6.
Flow chart of the proposed 3-stage encryption process.
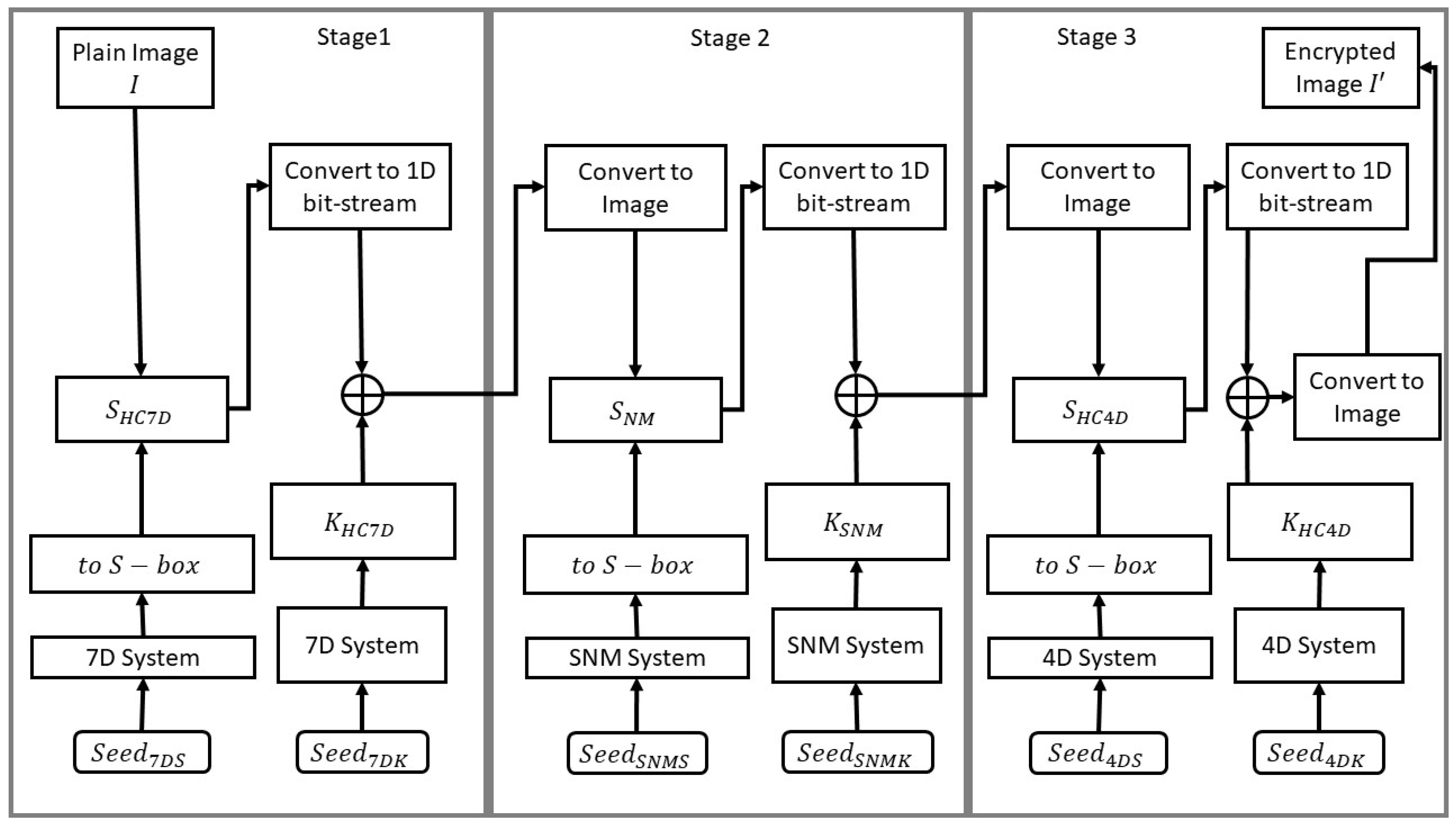
3.2. The Decryption Process
The following sequence of steps outline the proposed 3-stage decryption process. They are in a reverse order to those applied in the encryption process.
- Beginning with the 3-stage encrypted image of length M and width N.
-
Decryption stage 3: The 4D hyperchaotic system decryption key and inverse S-box.
- (a)
- The pixel values of the encrypted image are transformed into a bit-stream .
- (b)
- The encrypted data bits are XORed with the decryption key
- (c)
- The resulting encrypted data bits are converted into an image .
- (d)
- A reverse replacement process is applied to the image , employing , and resulting in image
-
Decryption stage 2: The single neuron model decryption key and inverse S-box.
- (a)
- The pixel values of the encrypted image are transformed into a bit-stream .
- (b)
- The encrypted data bits are XORed with the decryption key
- (c)
- The resulting encrypted data bits are converted into an image .
- (d)
- A reverse replacement process is applied to the image , employing , and resulting in image
-
Decryption stage 1: The 7D hyperchaotic system decryption key and inverse S-box.
- (a)
- The pixel values of the encrypted image are transformed into a bit-stream .
- (b)
- The encrypted data bits are XORed with the decryption key
- (c)
- The resulting encrypted data bits are converted into an image .
- (d)
- A reverse replacement process is applied to the image , employing , and resulting in a plain image I
A flow chart illustrative of the proposed 3-stage decryption process is provided in Figure 7.
Figure 7.
Flow chart of the proposed 3-stage decryption process.

3.3. Utilized Algorithms
Algorithm 1 describes the generation of an S-box given a pseudo-random bit-stream generated using one of the 3 PRNGs earlier proposed in Section 2. As discussed in SSection 2.4, towards treating the evaluation values of the S-box as part of the key space, Algorithm 1 attempts to achieve a certain set of provided values for S-box evaluations. The approach towards that is to generate an agreed upon number of S-boxes (which is a part of the key space as well), then each S-box is evaluated separately, and the chosen S-box is the one with performance evaluation values closer to the target values. Accordingly, it may come naturally to always provide optimal S-box evaluation values for every attempt of S-box generation. Nevertheless, fulfilling the need for complicating any cryptanalyses efforts, other, sub-optimal values may be provided resulting in the generation of different S-boxes. Such a decision would not affect the overall encryption process much as each generated S-box is only one component out of many stages. Therefore, performance evaluation of the encryption process is based on the integration of all the components in all 3 stages of the proposed encryption framework. Algorithm 2 elaborates the followed procedure in generating a PRNG bit-stream given the solution of a chaotic system.
| Algorithm 1:Generate an S-box given a bit-stream , the number of S-box trials n, and target performance metric values , and a bit-stream (an adaptation from that proposed in [14]) |
 |
| Algorithm 2:Generate a PRNG bit-stream given a chaotic system S of k dimensions, and the number of needed bits n (first proposed in [14]) |
 |
4. Numerical Results and Performance Evaluation
The performance of the proposed image encryption framework is provided in this section. A number of common performance evaluation metrics from the literature is utilized in this work [2,7,14]. Their mathematical expressions are provided in Table 4 and Table 17. The carried out tests aim to gauge the security, robustness and efficiency of the proposed framework at eradicating any identifiable information from the output encrypted images, such that they are completely asymmetric to their plaintext versions. The proposed algorithm is implemented on a machine running on a macOS Catalina v.10.15.7 with 2.9 GHz 6-Core Intel® CoreTM i9 and 32 GB of 2400 MHz DDR4 RAM. The software of choice is Wolfram Mathematica® v.13.2. Common images found in the state-of-the-art are also utilized in this work, to allow for a comparative analysis. All images are 256 pixels in length and 256 pixels in width, unless stated otherwise.
4.1. Visual and Visual-Statistical Analyses
The first measure employed for testing the output encrypted images is an examination through the human visual system (HVS). It is clear from Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 that no relation whatsoever can be observed between the plain images and their encrypted versions (i.e. complete asymmetry is achieved). The same can be noticed for their respective histograms. The histograms of the encrypted images depict a rather uniform distribution of values, which characterises excellent encryption.
4.2. Statistical Analyses
The mean squared error (MSE), peak signal-to-noise ratio (PSNR) and maximum absolute error (MAE) between input plain images and output encrypted images are reported in Table 5, Table 6 and Table 7, respectively. It is clear from each of the tables that the computed values for the proposed image encryption algorithm are comparable or superior to the state-of-the art, with high MSE and MAE values, and thus low PSNR values, indicating excellent scrambling and randomization performance of the proposed image encryption framework.
As for Shannon’s information entropy, Table 8 displays the computed values for various encrypted images, and compares those values with the state-of-the-art. Excellent entropy performance of is showcased for the proposed image encryption framework, being superior or comparable to the counterpart algorithms.
The pixel cross correlation coefficient is a measure of the linear dependency between neighboring pixel values in an image. It quantifies how well the encryption process has scrambled the pixels and eliminated any spatial relationships. For a well encrypted image, should have a value close to 0, indicating little or no correlation between adjacent pixel values. Table 9 provides the values for various images, each computed in 3 directions (horizontal, vertical and diagonal). While the plain images have values close to 1, their encrypted versions have values close to 0. A visual illustration of this metric is provided as a set of 2D plots in Figure 14 for the Lena image, as well as in Figure 15, Figure 16 and Figure 17, respectively, for each of its RGB channels. While sub-figures (c) and (f) of Figure 13 provide 3D plots of the same metric for the House image. It is clear that the plots of encrypted images exhibit a uniform distribution of values, unlike those of their plain versions. Table 10 and Table 11 display a comparison of with the state-of-the-art, utilizing the Lena image and each of its RGB channels, respectively. The computed values are shown to be near 0, as is the case in the state-of-the-art, in each of the tables.
Table 4.
Performance evaluation metrics and their mathematical expressions.
| Metric | Mathematical Expression |
|---|---|
| MSE |
|
| PSNR |
|
| MAE | |
| Entropy |
|
| DFT |
|
| CC |
|
| NPCR |
|
| UACI |
Another interesting manner of examining the pixel cross correlation among pixels would be to do so in the Fourier domain. By generating the discrete Fourier transform (DFT) of the plain and encrypted House image, as shown in sub-figures (b) and (e) of Figure 13 and visually examining them. The presence of a bright star-like shape at the center of the DFT plain image is characteristic of a normal plain image which has pixels depicting edges and corners. This is unlike the DFT encrypted image, which lacks any identifying visual characteristics.
Since randomness is an integral measure of any image encryption algorithm, an objective quantitative measure of it should be utilized. This is best carried out through a National Institute of Standards and Technology (NIST) SP 800 analysis [36]. In brief, a NIST analysis tests a bit-stream for a number of characteristics, including its randomness, as a well as quantifies its randomness and detects structural weaknesses. Such an analysis provides empirical evidence of the suitability of a PRNG’s use in cryptography applications. Table 12 presents the results of a NIST analysis carried out on a bit-stream depicting the data of an encrypted Girl image. All NIST tests are successfully passed, with scored values greater than .
Table 5.
MSE values for various images, for the proposed algorithm and the state-of-the-art.
| Image | Proposed | [7] | [16] | [37] | [17] | [6] | [21] | [14] |
|---|---|---|---|---|---|---|---|---|
| Lena | N/A | |||||||
| Mandrill | N/A | |||||||
| Peppers | N/A | N/A | ||||||
| House | N/A | N/A | N/A | N/A | ||||
| House2 | N/A | N/A | N/A | N/A | N/A | |||
| Girl | N/A | N/A | N/A | N/A | N/A | |||
| Sailboat | N/A | N/A | N/A | N/A | N/A | N/A | ||
| Tree | N/A | N/A | N/A | N/A | N/A | N/A | ||
| Average | 10900 | N/A |
Table 6.
PSNR values for various images, for the proposed algorithm and the state-of-the-art.
| Image | Proposed | [7] | [16] | [37] | [17] | [6] | [21] | [14] |
|---|---|---|---|---|---|---|---|---|
| Lena | ||||||||
| Mandrill | ||||||||
| Peppers | N/A | N/A | N/A | |||||
| House | N/A | N/A | N/A | N/A | ||||
| House2 | N/A | N/A | N/A | N/A | N/A | |||
| Girl | N/A | N/A | N/A | N/A | N/A | |||
| Sailboat | N/A | N/A | N/A | N/A | N/A | N/A | ||
| Tree | N/A | N/A | N/A | N/A | N/A | N/A | ||
| Average |
Table 7.
PSNR values for various images, for the proposed algorithm and the state-of-the-art.
| Image | Proposed | [7] | [6] | [37] | [38] | [21] | [14] |
|---|---|---|---|---|---|---|---|
| Lena | 87 | ||||||
| Peppers | N/A | N/A | |||||
| Mandrill | 92 | ||||||
| House | N/A | N/A | N/A | N/A | N/A | ||
| House 2 | N/A | N/A | N/A | N/A | N/A | ||
| Girl | N/A | N/A | N/A | N/A | N/A | ||
| Sailboat | N/A | N/A | N/A | N/A | N/A | ||
| Tree | N/A | N/A | N/A | N/A | N/A | ||
| Average |
Table 8.
Entropy values for various images, for the proposed algorithm and the state-of-the-art.
| Image | Proposed | [7] | [16] | [37] | [39] | [17] | [6] | [21] | [14] |
|---|---|---|---|---|---|---|---|---|---|
| Lena | |||||||||
| Mandrill | N/A | ||||||||
| Peppers | N/A | N/A | |||||||
| House | N/A | N/A | N/A | N/A | N/A | ||||
| House2 | N/A | N/A | N/A | N/A | N/A | N/A | |||
| Girl | N/A | N/A | N/A | N/A | N/A | N/A | |||
| Sailboat | N/A | N/A | N/A | N/A | N/A | N/A | N/A | ||
| Tree | N/A | N/A | N/A | N/A | N/A | N/A | N/A | ||
| Average |
Figure 13.
House image alongside its Fourier transformation and 3D plot of its pixel cross-correlation matrix pre- and post-encryption.
Figure 13.
House image alongside its Fourier transformation and 3D plot of its pixel cross-correlation matrix pre- and post-encryption.

Table 9.
Correlation coefficient values for various plain and encrypted images.
| Plain Image | Encrypted Image | |||||
|---|---|---|---|---|---|---|
| Correlation Coefficient | Correlation Coefficient | |||||
| Image | Horizontal | Diagonal | Vertical | Horizontal | Diagonal | Vertical |
| Lena | ||||||
| Mandrill | ||||||
| Peppers | ||||||
| House | ||||||
| House2 | ||||||
| Girl | ||||||
| Sailboat | ||||||
| Tree | ||||||
Table 10.
Correlation coefficient values comparison with the state-of-the-art, for an encrypted Lena image.
Table 10.
Correlation coefficient values comparison with the state-of-the-art, for an encrypted Lena image.
| Algorithm | Horizontal | Diagonal | Vertical |
|---|---|---|---|
| Proposed | |||
| [6] | |||
| [7] | |||
| [14] | |||
| [19] | |||
| [21] | |||
| [24] | |||
| [37] |
Table 11.
Color channel separated correlation coefficient value comparison with the state-of-the-art, for the Lena image.
Table 11.
Color channel separated correlation coefficient value comparison with the state-of-the-art, for the Lena image.
| Channel | Direction | Plain image | Encrypted image | [25] | [26] | [27] | [6] |
|---|---|---|---|---|---|---|---|
| Red | Horizontal | ||||||
| Diagonal | |||||||
| Vertical | |||||||
| Green | Horizontal | ||||||
| Diagonal | |||||||
| Vertical | |||||||
| Blue | Horizontal | ||||||
| Diagonal | |||||||
| Vertical |
Figure 14.
2D plot of pixel cross-correlation matrices of the Lena image pre- and post-encryption.
Figure 15.
2D plot of pixel cross-correlation matrices of the red channel of the Lena image pre- and post-encryption.
Figure 15.
2D plot of pixel cross-correlation matrices of the red channel of the Lena image pre- and post-encryption.
Figure 16.
2D plot of pixel cross-correlation matrices of the green channel of the Lena image pre- and post-encryption.
Figure 16.
2D plot of pixel cross-correlation matrices of the green channel of the Lena image pre- and post-encryption.
Figure 17.
2D plot of pixel cross-correlation matrices of the blue channel of the Lena image pre- and post-encryption.
Figure 17.
2D plot of pixel cross-correlation matrices of the blue channel of the Lena image pre- and post-encryption.
Table 12.
NIST analysis on Girl encrypted image.
| Test Name | Value | Remarks |
|---|---|---|
| Frequency | Success | |
| Block Frequency | Success | |
| Run | Success | |
| Longest run of ones | Success | |
| Rank | Success | |
| Spectral FFT | Success | |
| Non overlapping | Success | |
| Overlapping | Success | |
| Universal | Success | |
| Linear complexity | Success | |
| Serial | Success | |
| Approximate Entropy | Success | |
| Cumulative sum (forward) | Success | |
| Cumulative sum (reverse) | Success |
4.3. Differential Attack Analysis
A differential attack analysis is a type of cryptanalytic attack on encryption algorithms where an attacker analyzes the effect of specific changes in the input text on the output ciphertext. For example, the change of a single bit in the input plain image. By analyzing these differences, the attacker may be able to deduce information about the key or algorithm used. Two tests are commonly employed in the literature for such an analysis: The number of pixel change ratio (NPCR) for pixel-by-pixel comparison and the unified averaged change intensity (UACI) for the evaluation of the mean average difference [40], with ideal values for well-encrypted images being and , respectively. The mathematical expressions corresponding to each of those metrics are provided in Table 4. The computed NPCR and UACI values for various images are displayed in Table 13, with achieved average values of and , respectively, reflecting excellent performance. Table 14 compares the computed values with the state-of-the-art, for the RGB channels of various images. As expected, a comparable performance is achieved. Moreover, Table 15, displays another comparison with counterpart algorithms, for the Lena image. Once again, a comparable performance is achieved.
4.4. Key Space Analysis
It is of vital importance to carry out a key space analysis of any image encryption technique. Such an analysis quantifies how much information (in bits) is required to specify an encryption key. The more bits needed, the larger the key space. Consequently, a large key space makes brute force attacks infeasible. The larger the number of possible keys, the greater the resources and time required to try every key. This helps ensure encryption is secure against brute force cracking. In the proposed image encryption framework, the attained key space is vast, mainly due to the utilization of the hyperchaotic maps. The 4D hyperchaotic map employs 4 initial values and 7 constants, the 7D hyperchaotic map employs 7 initial conditions and 10 constants, while the SNM employs a total of 5 variables only. For each of the 3 S-boxes, 5 specific values for the metrics are chosen. This gives a total of variables in the computation of the key space. The computer and software package used to implement the proposed image encryption framework have a machine precision of . Ultimately, this gives a key space of . This computed value far surpasses the threshold suggested earlier in the literature [44], of , for successful resistance to brute-force attacks. A comparative analysis is carried out with the state-of-the-art in Table 16, showcasing the superior key space of the proposed image encryption framework.
4.5. Histogram Dependency Tests
In this testing perspective, the histograms of the plain and encrypted images are statistically compared in order to show the lack of statistical dependence between the two. Table 17 shows the five utilized tests (Blomqvist , Goodman-Kruskal , Kendall , Spearman , and Pearson r) and their mathematical expressions [45]. Table 18 demonstrates the results of applying these tests on a variety of images. As seen in the table, most of the resulting values are approaching 0, which shows the lack of any statistical dependency between every plain image and its encrypted version.
Table 17.
Histogram dependency tests and their mathematical expressions.
| Metric | Mathematical Expression |
|---|---|
| Blomqvist | |
| Goodman-Kruskal | |
| Kendall | |
| Spearman | |
| Pearson |
Table 18.
Tests of histogram dependency for various images.
| Image | Color | (28) | (29) | (30) | (31) | r (32) |
|---|---|---|---|---|---|---|
| Lena | Red | |||||
| Green | 0 | |||||
| Blue | ||||||
| Combined | ||||||
| Peppers | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined | ||||||
| Mandrill | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined | ||||||
| House | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined | ||||||
| House2 | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined | ||||||
| Girl | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined | ||||||
| Sailboat | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined | ||||||
| Tree | Red | |||||
| Green | ||||||
| Blue | ||||||
| Combined |
4.6. Execution Time Analysis
The execution time of an image encryption algorithm is an important metric, as it allows for a comparison of the efficiency and performance of different algorithms, as well as provides an estimation of the computational resources required for software and hardware implementation. Moreover, an analysis of the execution time reveals the applicability of an algorithm for real-time image encryption applications. The software implementation of the proposed image encryption framework is carried out over Wolfram Mathematica® v.13.2. The algorithm’s execution time is optimized through parallel processing over the 6 cores of the Intel® CoreTM i9 processor. The full details of the computing environment were provided in the first paragraph of Section 4. Table 19 reports the attained execution times of the Lena image, at various dimensions. These times result in an average encryption rate of Mbps. Moreover, Table 20 provides a comparative analysis with the state-of-the-art algorithms. The superiority of the proposed framework is clear, with the attained encryption times being much shorter in comparison to its counterparts, irrespective of the machine specifications.
4.7. S-Box Performance Analysis
The proposed S-boxes are evaluated in this section independently from the proposed framework’s performance as a whole. This is because an S-box is a consistent element that is nearly always at the core of image encryption algorithms and is tasked with applying Shannon’s property of confusion. In order to evaluate the ability of an S-box to cause confusion, 5 metrics are commonly computed [46]. These are the non-linearity (NL), linear approximation probability (LAP), differential approximation probability (DAP), bit independence criterion (BIC) and strict avalanche criterion (SAC). They are calculated for the proposed S-boxes (shown in Table 1, Table 2 and Table 3) and compared to those reported in the state-of-the-art, as well as to the ideal values. While all 3 proposed S-boxes exhibit comparable performance to counterpart algorithms from the literature, it is clear that the S-boxes constructed from the hyperchaotic functions perform better than the S-box constructed from the SNM. This is an advantage of hyperchaotic functions [47]. As in [14], and as described earlier in SSection 3.3, upon designing and constructing each of the proposed S-boxes, the aim is not to reach the ideal values of the metrics, but rather to reach a set of target metrics that are in close proximity to the ideal ones. This was carried out so as to include this set of target values as part of the key space, expanding it by variables, and allowing it to reach a key space of , as explained earlier in SSection 4.4.
Table 21.
Comparison of the numerical evaluation of the proposed S-boxes (displayed in Table 1, Table 2 and Table 3) among those provided in the literature.
| S-box | NL | SAC | BIC | LAP | DAP |
|---|---|---|---|---|---|
| Ideal values | 112 | 112 | |||
| Proposed, SNM (1) | 106 | 104 | |||
| Proposed, HC 4D (2) | 108 | 108 | |||
| Proposed, HC 7D (3) | 108 | 108 | |||
| [14] MT | 108 | 92 | |||
| [14] OpenSSL | 108 | 112 | |||
| [14] Intel’s MKL | 108 | 104 | |||
| [37] | 111 | 110 | |||
| [48] | 107 | ||||
| [49] | 100 | ||||
| [50] S4 | 112 | 112 |
5. Conclusions and Future Works
This work attempted to propose a novel framework for image encryption, capitalizing on the inherent characteristics of hyperchaotic functions and the simplicity of the single neuron model. Encryption was carried out over 3 stages, where in each stage the solution of one of the systems was numerically computed and used to generate a PRNG and construct an S-box. Next, the S-box was applied to scramble the image data, while an XOR operation with the encryption key was applied to randomize it. The main advantages of the proposed framework could be summarized in attaining a vast key space of and a high encryption rate of Mbps. Reaching such a key space is attributed to the usage of the hyperchaotic functions, while the efficiency of the framework is attributed to the optimization of its software implementation and making use of parallel processing over 6 cores. Moreover, the proposed framework was tested against an array of security tests, of quantitative and qualitative nature, and is shown to exhibit comparable or even superior performance, in comparison to the state-of-the-art.
Future research efforts could be dedicated to attempting to improve the efficiency of the proposed image encryption framework even more. This could be carried out through an enhanced parallel processing architecture, by running it over a network of connected machines, or better yet, implementing a hardware implementation (i.e. on an FPGA for example).
Author Contributions
Conceptualization, W.A., Y.L.C and L.Y.P; methodology, W.A. and M.G.; software, W.A. and M.G.; validation, W.A; writing—original draft preparation, W.A. and M.G.; writing—review and editing, W.A., Y.L.C and L.Y.P.; visualization, W.A.; supervision, W.A., Y.L.C and L.Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Council in Taiwan, grant number NSTC-109-2628-E-027-004–MY3, NSTC-111-2218-E-027-003, and NSTC-111-2622-8-027 -009 and the Ministry of Education of Taiwan, official document number 1112303249.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CA | Cellular Automata |
| DNA | Deoxyribonucleic acid |
| HVS | Human Visual System |
| MAE | Maximum absolute error |
| MSE | Mean Square Error |
| NIST | National Institute of Standards and Technology |
| NPCR | Number of Pixel Changing Ratio |
| PRNG | Pseudo-Random Number Generation |
| PSNR | Peak Signal-to-Noise Ratio |
| S-box | Substitution box |
| SNM | Single Neuron Model |
| SPN | Substitution-Permutation Network |
| UACI | Unified Averaged Change Intensity |
References
- Hosny, K.M.; Kamal, S.T.; Darwish, M.M. A color image encryption technique using block scrambling and chaos. Multimedia Tools and Applications 2022, pp. 1–21.
- Alexan, W.; Elkandoz, M.; Mashaly, M.; Azab, E.; Aboshousha, A. Color Image Encryption Through Chaos and KAA Map. IEEE Access 2023. [CrossRef]
- Alexan, W.; Mamdouh, E.; ElBeltagy, M.; Ashraf, A.; Moustafa, M.; Al-Qurashi, H. Social Engineering and Technical Security Fusion. 2022 International Telecommunications Conference (ITC-Egypt). IEEE, 2022, pp. 1–5.
- Jasra, B.; Moon, A.H. Color image encryption and authentication using dynamic DNA encoding and hyper chaotic system. Expert Systems with Applications 2022, 206, 117861. [CrossRef]
- Fang, J.; Jiang, M.; Yin, N.; Wei, D.; Zhang, Y. An image block encryption algorithm based on hyperchaotic system and DNA encoding. Multimedia Tools and Applications 2022, 81, 17245–17262. [CrossRef]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. Rgb image encryption through cellular automata, s-box and the lorenz system. Symmetry 2022, 14, 443. [CrossRef]
- Gabr, M.; Younis, H.; Ibrahim, M.; Alajmy, S.; Khalid, I.; Azab, E.; Elias, R.; Alexan, W. Application of DNA Coding, the Lorenz Differential Equations and a Variation of the Logistic Map in a Multi-Stage Cryptosystem. Symmetry 2022, 14, 2559. [CrossRef]
- Gabr, M.; Alexan, W.; Moussa, K. Image Encryption Through CA, Chaos and Lucas Sequence Based S-box. 2022 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA). IEEE, 2022, pp. 34–39.
- Gabr, M.; Hussein, H.H.; Alexan, W. A Combination of Decimal-and Bit-Level Secure Multimedia Transmission. 2022 Workshop on Microwave Theory and Techniques in Wireless Communications (MTTW). IEEE, 2022, pp. 177–182.
- Gabr, M.; Alexan, W.; Moussa, K.; Maged, B.; Mezar, A. Multi-Stage RGB Image Encryption. 2022 International Telecommunications Conference (ITC-Egypt). IEEE, 2022, pp. 1–6.
- Shannon, C.E. Communication theory of secrecy systems. The Bell system technical journal 1949, 28, 656–715. [CrossRef]
- Elqusy, A.S.; Essa, S.E.; El-Sayed, A. Key management techniques in wireless sensor networks. Commun Appl Electron (CAE) 2017, 7, 8–18.
- Shariatzadeh, M.; Rostami, M.J.; Eftekhari, M. Proposing a novel Dynamic AES for image encryption using a chaotic map key management approach. Optik 2021, 246, 167779. [CrossRef]
- Alexan, W.; Alexan, N.; Gabr, M. Multiple-Layer Image Encryption Utilizing Fractional-Order Chen Hyperchaotic Map and Cryptographically Secure PRNGs. Fractal and Fractional 2023, 7, 287. [CrossRef]
- Gabr, M.; Younis, H.; Ibrahim, M.; Alajmy, S.; Alexan, W. Visual Data Enciphering via DNA Encoding, S-Box, and Tent Mapping. 2022 IEEE 5th International Conference on Image Processing Applications and Systems (IPAS). IEEE, 2022, pp. 1–6.
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. Image Encryption Through Lucas Sequence, S-Box and Chaos Theory. 2021 8th NAFOSTED Conference on Information and Computer Science (NICS). IEEE, 2021, pp. 77–83.
- Younas, I.; Khan, M. A new efficient digital image encryption based on inverse left almost semi group and Lorenz chaotic system. Entropy 2018, 20, 913. [CrossRef]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. Lightweight image encryption: Cellular automata and the lorenz system. 2021 International Conference on Microelectronics (ICM). IEEE, 2021, pp. 34–39.
- Elkandoz, M.T.; Alexan, W. Image encryption based on a combination of multiple chaotic maps. Multimedia Tools and Applications 2022, pp. 1–22.
- ElBeltagy, M.; Alexan, W.; Elkhamry, A.; Moustafa, M.; Hussein, H.H. Image Encryption Through Rössler System, PRNG S-Box and Recamán’s Sequence. 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC). IEEE, 2022, pp. 0716–0722.
- Iqbal, N.; Naqvi, R.A.; Atif, M.; Khan, M.A.; Hanif, M.; Abbas, S.; Hussain, D. On the Image Encryption Algorithm Based on the Chaotic System, DNA Encoding, and Castle. IEEE Access 2021, 9, 118253–118270. [CrossRef]
- ur Rehman, A.; Liao, X.; Ashraf, R.; Ullah, S.; Wang, H. A color image encryption technique using exclusive-OR with DNA complementary rules based on chaos theory and SHA-2. Optik 2018, 159, 348–367. [CrossRef]
- Yang, B.; Liao, X. A new color image encryption scheme based on logistic map over the finite field ZN. Multimedia Tools and Applications 2018, 77, 21803–21821. [CrossRef]
- Wang, Y.; Wu, C.; Kang, S.; Wang, Q.; Mikulovich, V. Multi-channel chaotic encryption algorithm for color image based on DNA coding. Multimedia Tools and Applications 2020, pp. 1–26.
- Zhang, Y.Q.; He, Y.; Li, P.; Wang, X.Y. A new color image encryption scheme based on 2DNLCML system and genetic operations. Optics and Lasers in Engineering 2020, 128, 106040. [CrossRef]
- Jithin, K.; Sankar, S. Colour image encryption algorithm combining, Arnold map, DNA sequence operation, and a Mandelbrot set. Journal of Information Security and Applications 2020, 50, 102428. [CrossRef]
- Rehman, A.U.; Firdous, A.; Iqbal, S.; Abbas, Z.; Shahid, M.M.A.; Wang, H.; Ullah, F. A Color Image Encryption Algorithm Based on One Time Key, Chaos Theory, and Concept of Rotor Machine. IEEE Access 2020, 8, 172275–172295. [CrossRef]
- Li, B.; Liao, X.; Jiang, Y. A novel image encryption scheme based on logistic map and dynatomic modular curve. Multimedia Tools and Applications 2018, 77, 8911–8938. [CrossRef]
- Hu, X.; Wei, L.; Chen, W.; Chen, Q.; Guo, Y. Color image encryption algorithm based on dynamic chaos and matrix convolution. IEEE Access 2020, 8, 12452–12466. [CrossRef]
- Zhang, X.; Wang, L.; Wang, Y.; Niu, Y.; Li, Y. An image encryption algorithm based on hyperchaotic system and variable-step Josephus problem. International Journal of Optics 2020, 2020. [CrossRef]
- Gong, L.; Qiu, K.; Deng, C.; Zhou, N. An image compression and encryption algorithm based on chaotic system and compressive sensing. Optics & Laser Technology 2019, 115, 257–267.
- Li, C.; Chen, G. Coexisting chaotic attractors in a single neuron model with adapting feedback synapse. Chaos, Solitons & Fractals 2005, 23, 1599–1604.
- Qi, G.; van Wyk, B.J.; van Wyk, M.A. A four-wing attractor and its analysis. Chaos, Solitons & Fractals 2009, 40, 2016–2030.
- Cui, N.; Li, J. A new 4D hyperchaotic system and its control. AIMS Mathematics 2023, 8, 905–923. [CrossRef]
- Yang, Q.; Zhu, D.; Yang, L. A new 7D hyperchaotic system with five positive Lyapunov exponents coined. International Journal of Bifurcation and Chaos 2018, 28, 1850057. [CrossRef]
- Bassham, L.E.I.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.D.; Vangel, M.; Banks, D.L.; Heckert, A.; Dray, J.; Vo, S. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Revised 800-22, National Institute of Standards and Technology, 2010.
- Khan, M.; Masood, F. A novel chaotic image encryption technique based on multiple discrete dynamical maps. Multimedia Tools and Applications 2019, 78, 26203–26222. [CrossRef]
- Khan, M.; Shah, T. An efficient chaotic image encryption scheme. Neural Computing and Applications 2015, 26, 1137–1148. [CrossRef]
- Liu, H.; Zhao, B.; Huang, L. Quantum image encryption scheme using Arnold transform and S-box scrambling. Entropy 2019, 21, 343. [CrossRef]
- Wu, Y.; Noonan, J.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38.
- Slimane, N.B.; Aouf, N.; Bouallegue, K.; Machhout, M. A novel chaotic image cryptosystem based on DNA sequence operations and single neuron model. Multimedia Tools and Applications 2018, 77, 30993–31019. [CrossRef]
- Paul, L.; Gracias, C.; Desai, A.; Thanikaiselvan, V.; Suba Shanthini, S.; Rengarajan, A. A novel colour image encryption scheme using dynamic DNA coding, chaotic maps, and SHA-2. Multimedia Tools and Applications 2022, pp. 1–22.
- Wu, X.; Kurths, J.; Kan, H. A robust and lossless DNA encryption scheme for color images. Multimedia Tools and Applications 2018, 77, 12349–12376. [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. International journal of bifurcation and chaos 2006, 16, 2129–2151. [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A. The correlation coefficient: An overview. Critical reviews in analytical chemistry 2006, 36, 41–59. [CrossRef]
- Mahmood Malik, M.S.; Ali, M.A.; Khan, M.A.; Ehatisham-Ul-Haq, M.; Shah, S.N.M.; Rehman, M.; Ahmad, W. Generation of Highly Nonlinear and Dynamic AES Substitution-Boxes (S-Boxes) Using Chaos-Based Rotational Matrices. IEEE Access 2020, 8, 35682–35695. [CrossRef]
- Hosny, K.M.; Kamal, S.T.; Darwish, M.M. Novel encryption for color images using fractional-order hyperchaotic system. Journal of Ambient Intelligence and Humanized Computing 2022, 13, 973–988. [CrossRef]
- Zahid, A.H.; Arshad, M.J.; Ahmad, M. A novel construction of efficient substitution-boxes using cubic fractional transformation. Entropy 2019, 21, 245. [CrossRef]
- Hayat, U.; Azam, N.A.; Asif, M. A method of generating 8× 8 substitution boxes based on elliptic curves. Wireless Personal Communications 2018, 101, 439–451. [CrossRef]
- Siddiqui, N.; Yousaf, F.; Murtaza, F.; Ehatisham-ul Haq, M.; Ashraf, M.U.; Alghamdi, A.M.; Alfakeeh, A.S. A highly nonlinear substitution-box (S-box) design using action of modular group on a projective line over a finite field. PLOS one 2020, 15, e0241890. [CrossRef]
Figure 1.
A plot of .

Figure 2.
The connected chaotic attractor for the SNM at .

Figure 3.
Lyapunov exponent plot for the SNM at .
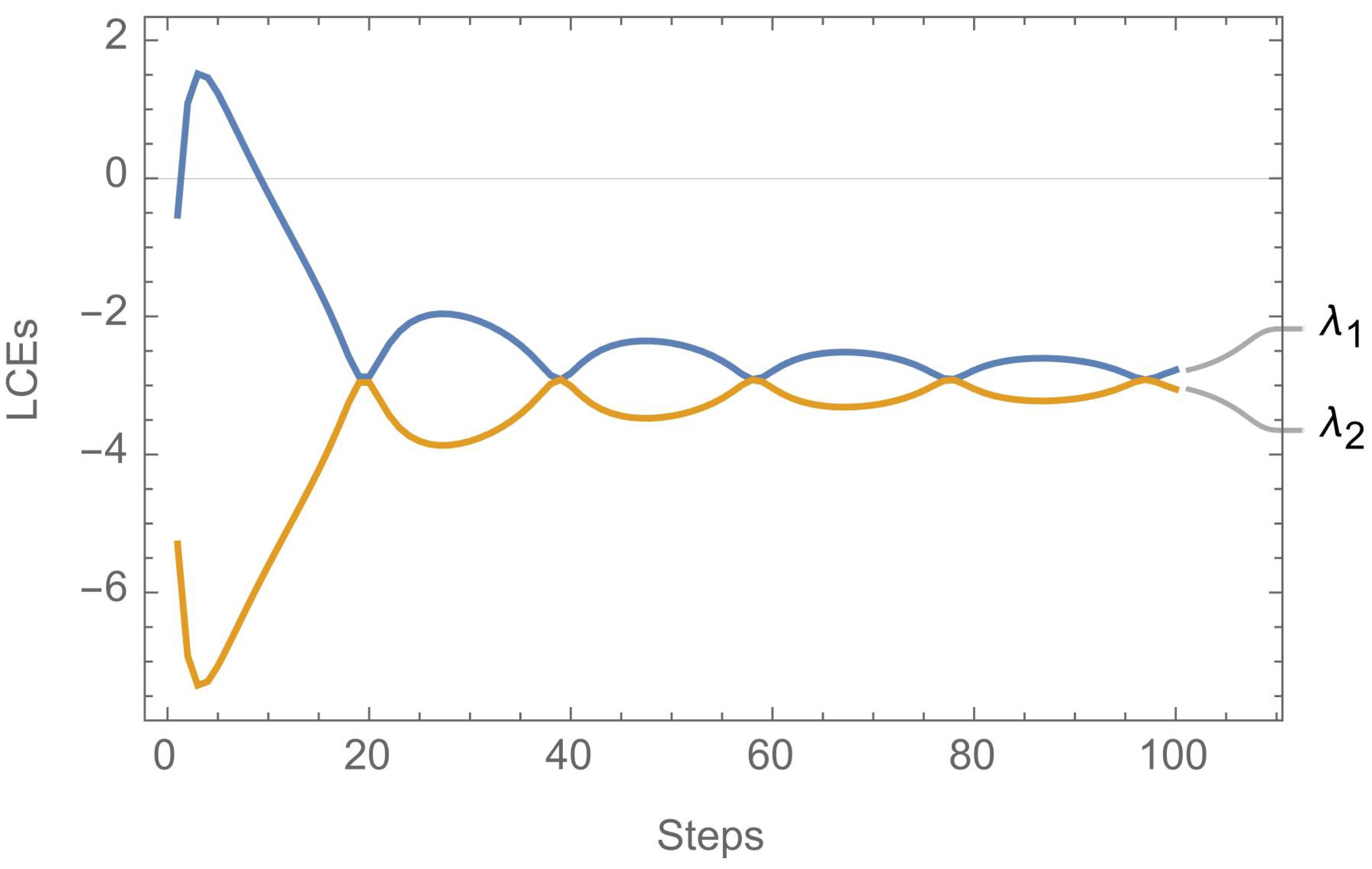
Figure 5.
Hyperchaotic attractors for the system (3) with , shown for various 3D spaces.
Figure 5.
Hyperchaotic attractors for the system (3) with , shown for various 3D spaces.
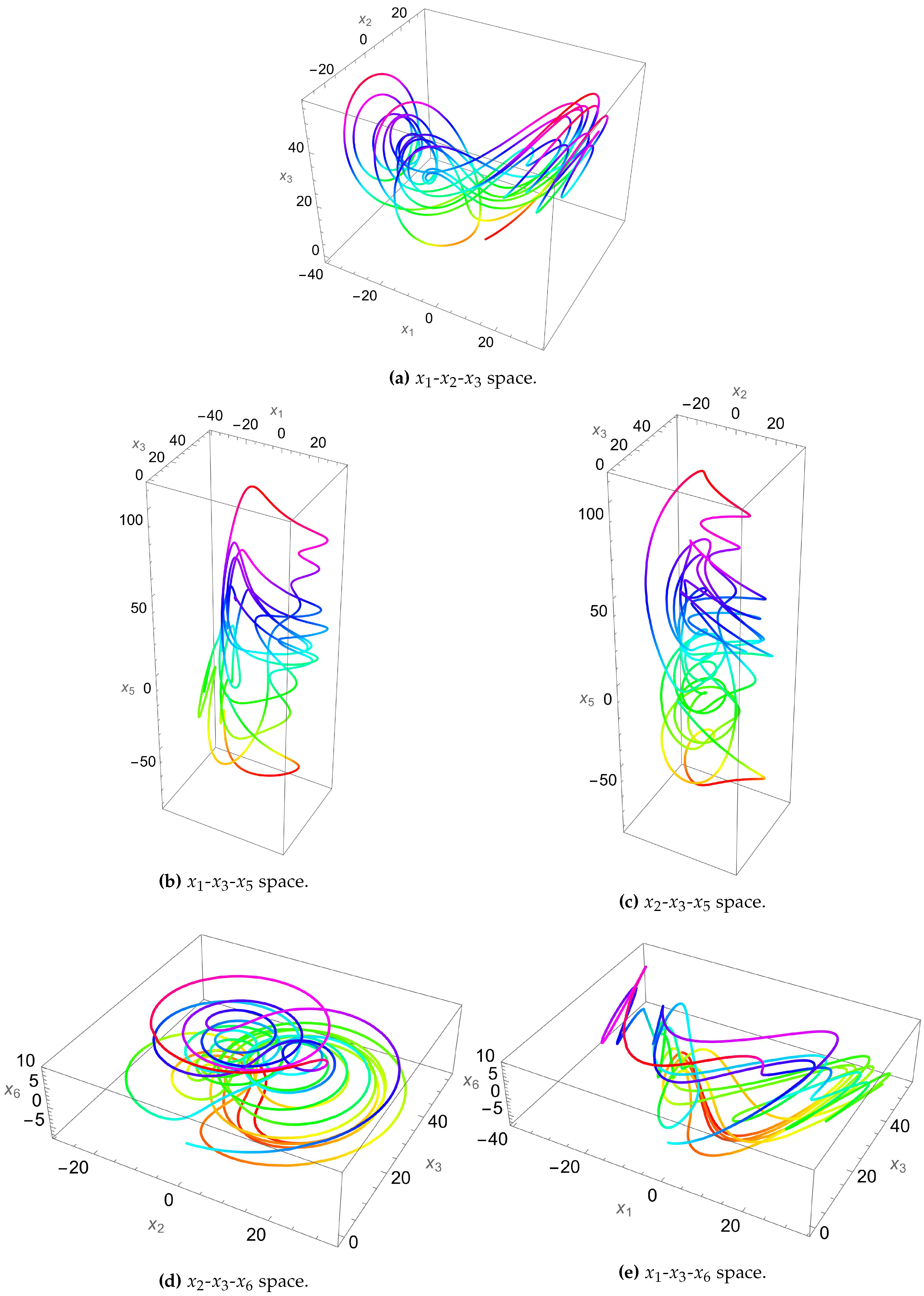
Figure 8.
Mandrill image and histogram comparison of the plain and encrypted versions.

Figure 9.
Peppers image and histogram comparison of the plain and encrypted versions.
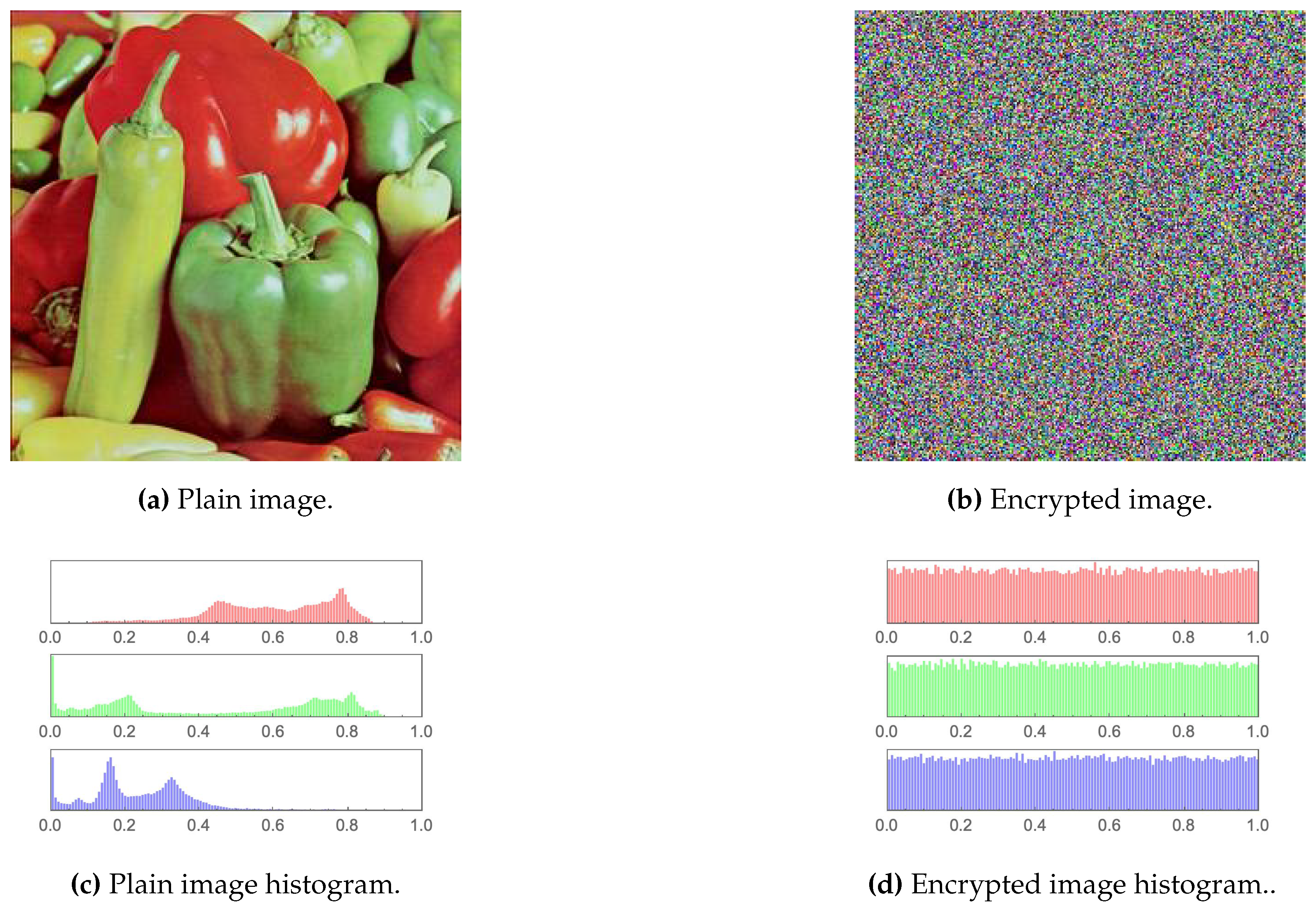
Figure 10.
Sailboat image and histogram comparison of the plain and encrypted versions.

Figure 11.
Tree image and histogram comparison of the plain and encrypted versions.
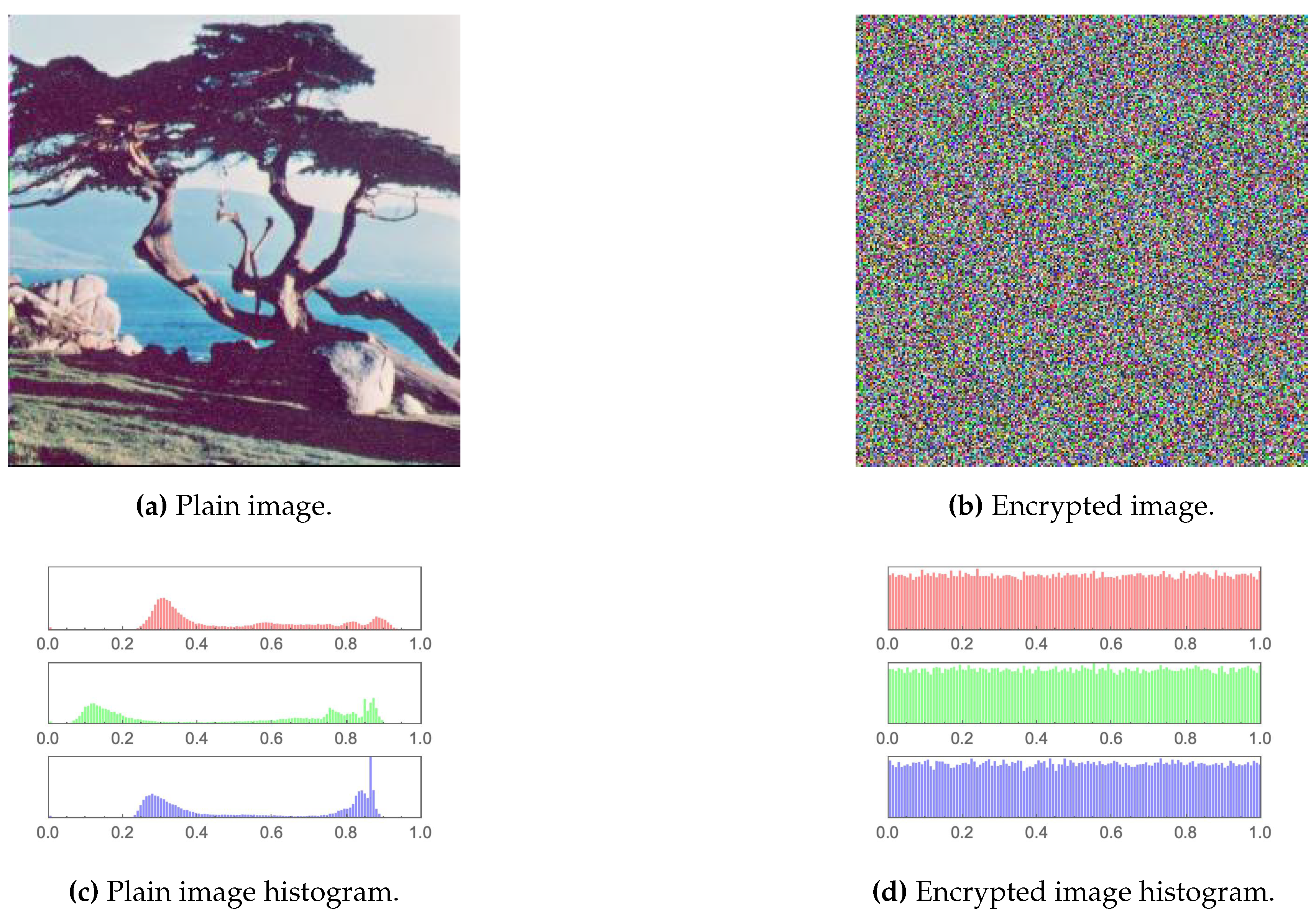
Figure 12.
House2 image and histogram comparison of the plain and encrypted versions.
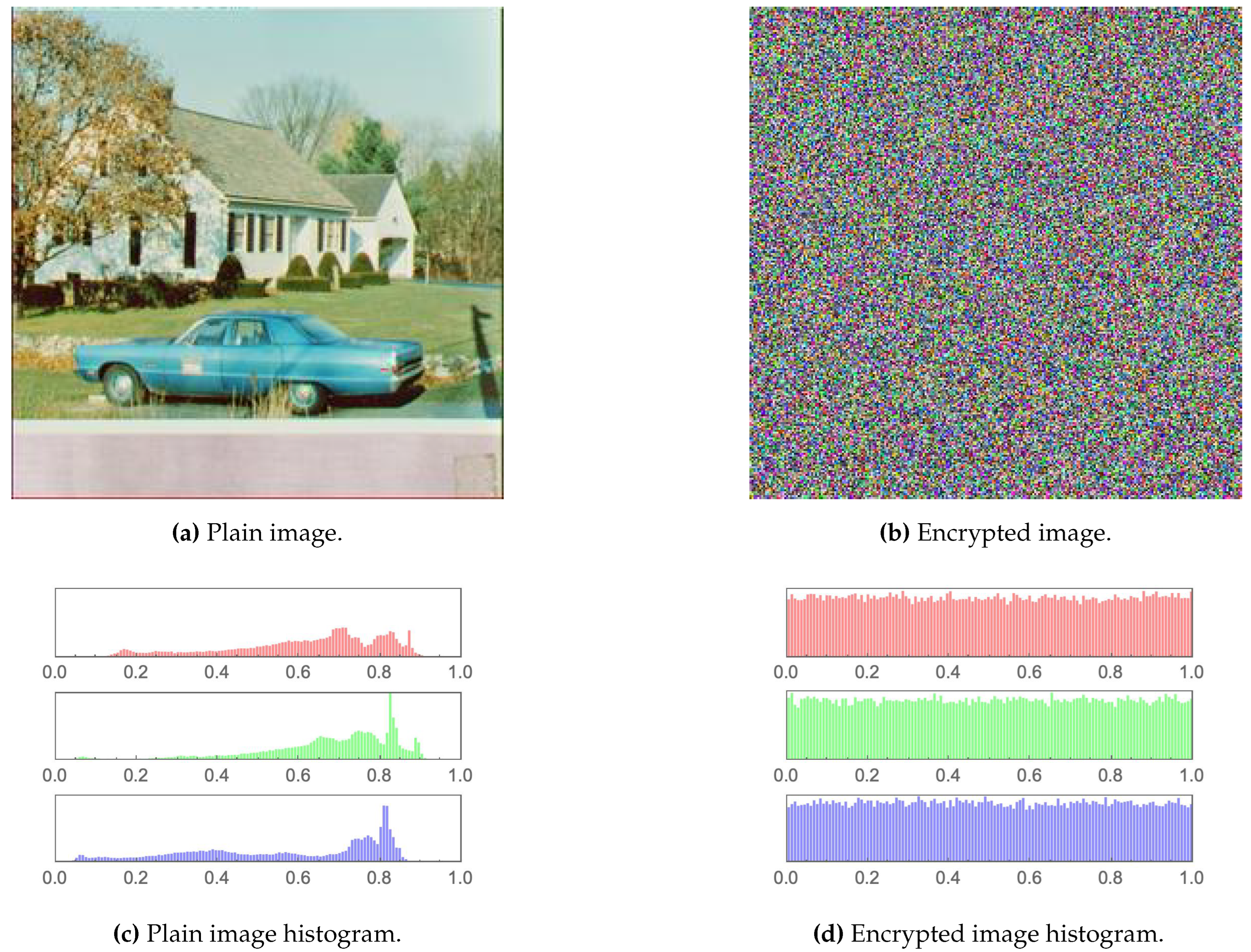
Table 1.
7D hyperchaotic system based S-box.
| 30 | 62 | 124 | 248 | 235 | 148 | 35 | 202 | 143 | 22 | 43 | 85 | 170 | 76 | 161 | 48 |
| 129 | 2 | 253 | 231 | 190 | 93 | 153 | 60 | 50 | 100 | 198 | 75 | 151 | 11 | 61 | 212 |
| 4 | 228 | 167 | 111 | 220 | 142 | 13 | 89 | 210 | 118 | 237 | 168 | 25 | 51 | 101 | 197 |
| 174 | 38 | 78 | 152 | 54 | 41 | 17 | 65 | 105 | 183 | 29 | 64 | 112 | 215 | 94 | 214 |
| 10 | 125 | 74 | 56 | 16 | 242 | 136 | 6 | 122 | 147 | 132 | 251 | 146 | 28 | 18 | 34 |
| 69 | 130 | 95 | 217 | 52 | 102 | 191 | 126 | 113 | 79 | 0 | 119 | 223 | 40 | 82 | 141 |
| 3 | 120 | 236 | 109 | 162 | 159 | 137 | 115 | 45 | 177 | 239 | 222 | 86 | 171 | 63 | 186 |
| 241 | 21 | 42 | 200 | 175 | 123 | 12 | 68 | 110 | 234 | 218 | 145 | 221 | 199 | 149 | 24 |
| 47 | 91 | 179 | 88 | 157 | 55 | 140 | 255 | 14 | 250 | 213 | 138 | 194 | 66 | 58 | 108 |
| 207 | 131 | 172 | 70 | 165 | 71 | 187 | 44 | 240 | 107 | 243 | 227 | 67 | 182 | 232 | 211 |
| 7 | 23 | 32 | 73 | 133 | 184 | 163 | 173 | 98 | 192 | 117 | 230 | 208 | 158 | 128 | 225 |
| 196 | 81 | 144 | 9 | 33 | 247 | 39 | 169 | 185 | 104 | 77 | 31 | 164 | 114 | 229 | 204 |
| 189 | 103 | 226 | 166 | 57 | 46 | 96 | 249 | 15 | 178 | 181 | 155 | 49 | 106 | 244 | 209 |
| 26 | 201 | 135 | 20 | 139 | 246 | 238 | 245 | 180 | 176 | 156 | 72 | 193 | 116 | 84 | 83 |
| 252 | 254 | 195 | 53 | 27 | 134 | 205 | 87 | 97 | 219 | 127 | 150 | 121 | 99 | 188 | 154 |
| 160 | 37 | 216 | 80 | 224 | 19 | 233 | 59 | 1 | 90 | 206 | 36 | 203 | 8 | 5 | 92 |
Table 2.
SNM based S-box.
| 36 | 119 | 247 | 239 | 72 | 35 | 152 | 117 | 47 | 126 | 236 | 87 | 11 | 241 | 183 | 98 |
| 67 | 15 | 61 | 127 | 90 | 217 | 198 | 139 | 159 | 106 | 167 | 101 | 177 | 197 | 20 | 170 |
| 163 | 109 | 165 | 99 | 235 | 173 | 216 | 134 | 26 | 238 | 17 | 16 | 34 | 229 | 110 | 212 |
| 69 | 150 | 196 | 86 | 180 | 115 | 192 | 209 | 146 | 203 | 223 | 95 | 22 | 137 | 120 | 71 |
| 189 | 129 | 74 | 154 | 114 | 200 | 246 | 80 | 6 | 46 | 214 | 59 | 97 | 65 | 77 | 176 |
| 108 | 62 | 224 | 14 | 213 | 29 | 226 | 172 | 242 | 0 | 89 | 84 | 195 | 33 | 4 | 23 |
| 118 | 245 | 116 | 252 | 174 | 96 | 40 | 48 | 240 | 148 | 227 | 54 | 78 | 164 | 38 | 104 |
| 131 | 64 | 205 | 100 | 142 | 52 | 169 | 215 | 178 | 157 | 51 | 66 | 222 | 237 | 91 | 37 |
| 138 | 30 | 207 | 123 | 234 | 149 | 221 | 219 | 230 | 50 | 175 | 155 | 141 | 125 | 12 | 92 |
| 60 | 187 | 251 | 8 | 93 | 105 | 83 | 179 | 121 | 41 | 181 | 171 | 5 | 124 | 19 | 225 |
| 250 | 185 | 166 | 85 | 112 | 130 | 10 | 228 | 73 | 42 | 18 | 253 | 190 | 79 | 7 | 249 |
| 220 | 147 | 218 | 156 | 248 | 161 | 107 | 182 | 94 | 53 | 208 | 82 | 136 | 13 | 133 | 63 |
| 145 | 231 | 31 | 143 | 135 | 202 | 255 | 2 | 43 | 56 | 28 | 103 | 199 | 201 | 232 | 70 |
| 39 | 122 | 1 | 160 | 58 | 111 | 233 | 194 | 44 | 206 | 210 | 24 | 193 | 76 | 211 | 191 |
| 49 | 88 | 102 | 244 | 27 | 45 | 57 | 81 | 188 | 254 | 32 | 128 | 153 | 3 | 68 | 204 |
| 21 | 132 | 243 | 140 | 151 | 113 | 55 | 168 | 25 | 75 | 144 | 184 | 162 | 186 | 9 | 158 |
Table 3.
4D hyperchaotic system based S-box.
| 87 | 103 | 129 | 234 | 78 | 114 | 219 | 70 | 90 | 239 | 108 | 223 | 106 | 135 | 133 | 116 |
| 107 | 91 | 229 | 79 | 71 | 3 | 122 | 83 | 8 | 240 | 17 | 148 | 2 | 150 | 55 | 1 |
| 32 | 35 | 22 | 137 | 204 | 97 | 16 | 136 | 52 | 27 | 220 | 58 | 202 | 217 | 43 | 218 |
| 138 | 54 | 157 | 53 | 46 | 80 | 81 | 59 | 60 | 232 | 248 | 215 | 161 | 251 | 62 | 152 |
| 227 | 235 | 164 | 163 | 177 | 226 | 73 | 23 | 186 | 191 | 120 | 38 | 112 | 246 | 95 | 172 |
| 101 | 1 | 11 | 72 | 160 | 25 | 15 | 126 | 47 | 6 | 253 | 100 | 183 | 24 | 216 | 39 |
| 7 | 19 | 26 | 93 | 194 | 67 | 10 | 149 | 140 | 99 | 171 | 154 | 88 | 77 | 132 | 228 |
| 48 | 225 | 128 | 243 | 245 | 12 | 254 | 139 | 184 | 49 | 5 | 151 | 42 | 44 | 145 | 66 |
| 34 | 185 | 65 | 82 | 221 | 189 | 36 | 175 | 244 | 213 | 130 | 30 | 69 | 144 | 236 | 142 |
| 9 | 29 | 197 | 28 | 165 | 115 | 188 | 41 | 74 | 76 | 196 | 110 | 61 | 155 | 211 | 124 |
| 75 | 238 | 89 | 181 | 252 | 222 | 98 | 237 | 241 | 63 | 121 | 224 | 85 | 212 | 199 | 131 |
| 57 | 143 | 4 | 51 | 84 | 167 | 105 | 190 | 173 | 203 | 141 | 198 | 207 | 200 | 176 | 174 |
| 179 | 214 | 242 | 20 | 195 | 205 | 192 | 14 | 111 | 134 | 119 | 230 | 96 | 33 | 170 | 18 |
| 146 | 158 | 68 | 123 | 127 | 94 | 250 | 31 | 206 | 169 | 147 | 168 | 180 | 64 | 92 | 40 |
| 178 | 231 | 255 | 56 | 37 | 193 | 182 | 156 | 208 | 117 | 201 | 21 | 109 | 118 | 166 | 153 |
| 187 | 50 | 45 | 104 | 102 | 162 | 209 | 247 | 233 | 125 | 113 | 249 | 159 | 86 | 0 | 210 |
Table 13.
NPCR and UACI values of various images.
| Metric | Image | Result |
|---|---|---|
| NPCR | Lena | |
| Peppers | ||
| Mandrill | ||
| House | ||
| House2 | ||
| Girl | ||
| Sailboat | ||
| Tree | ||
| Average | ||
| UACI | Lena | |
| Peppers | ||
| Mandrill | ||
| House | ||
| House2 | ||
| Girl | ||
| Sailboat | ||
| Tree | ||
| Average |
Table 14.
NPCR and UACI values comparison with the state-of-the-art for various images.
| Metric | Image | Color Channel | Proposed | [6] | [41] | [14] |
|---|---|---|---|---|---|---|
| NPCR | Lena | Red | ||||
| Green | ||||||
| Blue | ||||||
| Peppers | Red | |||||
| Green | ||||||
| Blue | ||||||
| Mandrill | Red | |||||
| Green | ||||||
| Blue | ||||||
| UACI | Lena | Red | ||||
| Green | ||||||
| Blue | ||||||
| Peppers | Red | |||||
| Green | ||||||
| Blue | ||||||
| Mandrill | Red | |||||
| Green | ||||||
| Blue |
Table 15.
NPCR and UACI values comparison of the Lena image with the state-of-the-art.
| Scheme | NPCR | UACI |
|---|---|---|
| Proposed | ||
| [2] | ||
| [6] | ||
| [14] | ||
| [19] | ||
| [21] | ||
| [37] | ||
| [42] | ||
| [43] |
Table 16.
A comparison of key space values with the state-of-the-art.
| Algorithm | Key space |
|---|---|
| Proposed | |
| [2] | |
| [7] | |
| [14] | |
| [19] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [28] | |
| [29] |
Table 19.
Execution times, in terms of encryption, decryption, and their combined values for the proposed algorithm at various image dimensions.
Table 19.
Execution times, in terms of encryption, decryption, and their combined values for the proposed algorithm at various image dimensions.
| Image Dimensions | [s] | [s] | [s] |
|---|---|---|---|
Table 20.
A comparison of the encryption time for various algorithms from the literature for a Lena image with dimensions .
Table 20.
A comparison of the encryption time for various algorithms from the literature for a Lena image with dimensions .
| Algorithm | [s] | Machine specifications (CPU and RAM) |
|---|---|---|
| Proposed | 2.9 GHz Intel® CoreTM i9, 32 GB | |
| [2] | 3.4 GHz Intel®, N/A | |
| [6] | 2.9 GHz Intel® CoreTM i9, 32 GB | |
| [7] | 2.9 GHz Intel® CoreTM i9, 32 GB | |
| [14] | 2.9 GHz Intel® CoreTM i9, 32 GB | |
| [19] | 3.4 GHz Intel® CoreTM i7, 8 GB | |
| [21] | 2.7 GHz Intel® CoreTM i7, 8 GB | |
| [29] | N/A | |
| [30] | 3.4 GHz Intel® CoreTM i3, 4 GB | |
| [31] | 3.4 GHz Intel® CoreTM i7, 8 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated










