Preprint
Article
A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution
Altmetrics
Downloads
136
Views
16
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 April 2023
Posted:
27 April 2023
You are already at the latest version
Alerts
Abstract
To overcome the temperature effect of NaI(Tl) detectors for energy spectrometry without additional hardware, a new correction method was put forward based on pulse deconvolution, trapezoidal shaping and amplitude correction, named DTSAC. To verify this method, actual pulses from a NaI(Tl)-PMT detector were measured at different temperatures from -20℃ to 50℃. Pulse processing and spectrum synthesis showed that the position drift of the 662 keV peak was less than 3 keV, and the corresponding resolution at 662 keV of the sum spectra ranges from 6.9% to 10.60% with trapezoidal width set as 1000 ns to 100 ns. The DTSAC method corrects temperature effect by pulse processing, and need no reference peak, reference spectrum and additional circuits. The method solves the problem of correction of pulse shape and pulse amplitude at the same time, and can be used even at high counting rate.
Keywords:
Subject: Engineering - Energy and Fuel Technology
1. Introduction
NaI(Tl) detectors are the most widely used scintillation detectors due to their low price and good reliability [1]. But their radiation response has remarkable temperature effect[2,3,4], leading to unacceptable spectrum drift in field application with varying temperature. In addition, long luminescence decay time at low temperature [2,3,4] makes them unfit for high count rate applications. Temperature correction for NaI(Tl) detectors has generally been treated by three types of spectra stabilization methods. The first is to stabilize the position of some reference peaks by adjusting the high voltage of the photomultiplier tube (PMT) [5] or the gain of the amplifier [6,7]. The second is correcting continuously the spectra in time series [9,10,11] based on the reference peak [5,8] or the reference spectrum [9,10]. The last is to use a temperature-dependent correcting factor to correct the amplitude of each pulse[12]. The use of reference peak or reference spectrum requires notable peaks or stable radiation field, which are not always satisfied. Adjustment of high voltage or amplifier gain increases the complexity of the electronic system. The last method is attractive and has been applied in the commercial instrument identiFINDER[12]. However, none of the traditional methods can solve the difficult problem of high count rate application due to long decay time at low temperature.
In this paper, a new temperature correction method based on pulse processing was put forward to solve the problem of correction of pulse shape and pulse amplitude at the same time.
2. Materials and Methods
2.1. Method description
For the same energy deposition of the incident gamma ray, both of the decay time and the area of the pulses from the NaI(Tl) and PMT system varies with the temperature. In order to correct the two effects, a three-step pulse processing of the DTSAC method was designed, namely deconvolution[13,14], trapezoidal shaping[15], and amplitude correction[12], as shown in Figure 1. The first two steps correct the effect of temperature on pulse duration, and the latter step corrects the effect of temperature on pulse area. A uniform pulse model with different parameters was used to describe the NaI(Tl) pulses at different temperatures. In the deconvolution step, all pulses at different temperatures were deconvolved into quasi-δ pulses with invariant area. In the trapezoidal shaping step, quasi-δ pulses were shaped into trapezoidal pulses, ensuring each amplitude equal to the original pulse area. In the amplitude correction step, the amplitude values extracted from the trapezoidal pulses was corrected to be equal to those at the reference temperature according to a previously calibrated temperature response function.
2.1.1. Pulse model and deconvolution
The convolution pulse model in time domain proposed by Wuyun Xiao et al. [14,16] is used to describe the PMT anode pulse of the NaI(Tl) detectors, and it is rewritten as
where the asterisk(*) is a convolution operator, u(t) is the unit step function, A is the area of the pulse, σ is the standard deviation of the Gaussian function, M and N are the number of exponential components, τi and λj are the decay constants of the exponential functions, φi and ϕj are the proportions of each exponential components (calculated by area), which satisfy
In this model, the anode pulse signal is described as a convolution of three functions. The first one, f1(t), is a Gaussian function. The other two, f2(t) and f3(t), are the sum of several exponential functions. f1(t), f2(t) and f3(t) are all normalized functions of area instead of amplitude. The commonly used uni-exponential model, bi-exponential model, Gauss-exponent convolution model and others can be regarded as special cases of this model. Due to the influence of temperature, even for the same energy deposition, the parameters A、σ、τi、λj、φi and ϕj are all slowly varying functions of temperature T. Model parameters at specific temperature can be obtained by fitting the average pulse. The relationship between model parameters and temperature can be established by function fitting or interpolation.
The z transformation of f(t) is
where
Ts is the sampling period. According to [16], the original pulse f(t) can be deconvolved into a narrow Gaussian pulse A∙f1(t) with invariant area, and its z-domain expression is
where
D(z) is called deconvolution filter, and it is related to temperature T. ak is polynomial coefficient determined only by model parameters τi、λj、φi and ϕj. When M = 2, N = 1 and δ is very close to 0, a simplified model as (7) can be obtained. It is the convolution between an exponent function and the sum of two exponent functions.
In Equation (7), A is the pulse area, τ0 is the rising time constant, τ1 and τ2 represent the time constant of the fast component and the slow component respectively, and φ is the proportion of the fast component.
The z-domain expression of the deconvolution filter D(z) is
Ignoring the one period delay of the deconvolution result, the time domain algorithm can be expressed as
where
2.1.2. Trapezoidal shaping and amplitude correction
In the actual situation, the pulse deconvolution operation can cause two problems. One is the signal-to-noise ratio (SNR) decreasing remarkably; and the other is that the deconvolution pulses have different width because the parameter σ is dependent to temperature T. In order to improve the SNR, the trapezoidal filter is used to shape the deconvolution pulse, whose z-domain expression is
where na and nb are trapezoidal parameters, and tTop = (nb-na)Ts and tWidth = (nb+na)Ts are the time width of flat-top and bottom respectively. In order to avoid ballistic deficit caused by σ(T), it is required that tTop > 6σmax, which can be easily met since σ is generally about 10 ns. Trapezoidal parameters can be selected according to the pulse count rate to achieve the balance between pulse throughput and energy resolution.
If the actual pulse is exactly consistent with the pulse model, the amplitude HT of the trapezoidal pulse will be equal to the original pulse area A. Considering the inaccuracy of the pulse model, the model error correction factor κ is introduced to make κHT = A, and κ is a function of temperature and trapezoidal parameters, denoted as κ(T,na,nb). The more accurate the model is, the closer to 1 the value of κ would be. The area A of the original pulse for γ-rays with specific energy is mainly determined by the light yield of the scintillator and the PMT gain, both of which are affected by temperature[12]. The area of original pulse at temperature T is denoted as A(T), and the one at reference temperature T0 is denoted as A0. Equation (12) can be obtained while introducing the area correction factor ε(T) = A0/A(T).
ε′(T,na,nb) = ε(T)κ(T,na,nb) is called the amplitude correction factor. The corrected trapezoidal height is equal to the area of the original pulse at the reference temperature, which is independent of temperature, so as to achieve spectrum stabilization. The correction result calculated by ε has some deviation due to the model error, while the one calculated by ε′ is more accurate. However, ε is easy to use, since it is independent of trapezoidal parameters, while ε′ should be calculated according to trapezoidal parameters.
2.2. Pulse data acquisition and preprocessing
A NaI(Tl) detector of 2 inches diameter coupled with a CR173-01 PMT was used, and 1 μCi 137Cs point source was located near to its front end. The experiments were carried out in a Kewen KW-TH-100X-PC thermostatic chamber. The pulses were collected at several temperature points from -20℃ to 50℃ with a step of 10℃. The temperature changing rate was controlled within 5℃/h in order to protect the NaI(Tl) crystal. Each temperature point was maintained constant for 8 h to ensure thermal balance, and the pulses were collected in the last 30 min by a CAEN 6730 digitizer (12-bit, sampling frequency 500 MHz ADC). The pulse recording length was 8 μs and 1 μs before triggering was reserved as its baseline. The baseline of each pulse was estimated and then substracted from the recorded pulse. After eliminating the data with pulse amplitude beyond the dynamic range and the data with multiple pulses within acquisition time, 200,000 pulses were obtained at each temperature point. Pulses from the 662 keV photoelectric peak were picked out according to the pulse area.
3. Results
3.1. Pulse model parameter fit result
The selected pulses were aligned and used to calculate the average pulse at each temperature (Figure 2). The results show that the luminescence decay time of the NaI(Tl) scintillators decreases with the increase of temperature, which is consistent with the literatures [2,3,4].
The pulse model in section 2.1.1 has too many parameters to fit, so the number of parameters should be appropriately reduced to facilitate fitting. Some special cases including Gauss-exponent convolution model, exponent-exponent convolution model (bi-exponential model), Gauss-double exponent sum convolution model, and exponent-double exponent sum convolution model were used to fit the average pulses at different temperatures. The pulse arrival time was taken as a fit parameter, and the pulse area was fixed to take the average pulse area. The fit results of the first two models were not sensitive to initial values due to few fit parameters, so the Levenberg-Marquardt algorithm with roughly selected initial values was used for fitting. The fit results of the last two models were sensitive to initial values due to too many fit parameters. An iterative process of alternating optimization was used, and the fit results of the first two models were adopted as the initial values. The R2 values fitted by each model are shown in Figure 3. It can be seen that the exponent-double exponent sum convolution model is the best, with its R2 values ranging from 0.9980 to 0.9994. The fit parameters are shown in Table 1.
3.2. Temperature correction result
At different temperatures, the actual pulses from 662 keV are shown in Figure 4, compared with their deconvolution results, and their further trapezoidal shaping results with different parameters. It looks difficult to identify the quasi-δ pulse in the deconvolution signal because of low SNR. After shaping, the trapezoidal pulses are very obvious. All of the trapezoids have almost the same shape only with different amplitude caused by different temperature. The random fluctuation of trapezoidal flat-top decreases with the increase of pulse width tWidth.
As shown in Figure 4(d), the amplitude values of all trapezoidal pulses extracted at the center of their flat-top were corrected by ε and ε′ separately. The average areas of 662 keV pulses at different temperatures were used to calculate ε, and the average amplitude of the corresponding trapezoidal pulses were used to calculate ε′. The relationship between 1/ε (1/ε′) and temperature are shown in Figure 5.
The quadratic function
was used to fit the relationship between T and 1/ε (1/ε’). The fit results of ε and ε’ for different trapezoidal parameters are shown in Table 2.
As shown in Table 2, the relationships between T and 1/ε(1/ε’) are in good agreement with the quadratic function, and the R2 values are all above 0.9993.
All pulse amplitudes corrected by ε and ε′ calculated by fitted quadratic function at each temperature were sorted and counted into a spectrum of 1000 channels with proper channel width. As comparison, the gated integration with different integration period from 1000 ns to 7000 ns were performed on the actual pulses, and the amplitude results were converted into spectra in the same way. The gamma spectra at different temperatures obtained by the four processing methods are shown in Figure 6. As can be seen, the spectra obtained by gated integration have obvious spectrum drift at different temperatures, and the spectrum drift of 7000 ns is more obvious than that of 1000 ns. That is because the pulse area decreases with the increase of temperature, and the luminescence decay time decreases with the increase of temperature. The increase of the total area and the incomplete integration counteract each other to a certain extent when the gated integration time is shorter. But in Figure 6 (c) and (d), after correction with the proposed method, the variation of the peak positions of different temperature is controlled within very small range. Especially for the last one, the peak position looks almost independent of temperature when the amplitude correction factor ε’ is used.
The overall drifting range of the 662 keV peak position of the four methods are 62.9, 124.9, 11.2 and 1.4 channels respectively. Because the trigger threshold for pulse acquisition was a bit high, the X-ray peaks of 32 keV were cut off from the spectra.
Figure 7 shows the sum spectra added together with the spectra of different temperatures. It can be seen that the two sum spectra obtained by gated integration methods distorted significantly. But the other two sum spectra obtained with the proposed method are satisfying. The shape of the 662 keV peak looks very close to Gaussian distribution, with calculated values of energy resolution as 7.23% and 6.91% for ε and ε′ respectively. With temperature ranging from -20℃ to 50℃, the lowest position drift of the main peak was less than 3 keV. It means the temperature effect of the NaI(Tl) detector was removed accurately.
In order to study the influence of different trapezoidal parameters on energy resolution of the sum spectra, different parameters with tWidth = 100~1800 ns and flat-top ratio of 0~0.9 were used for trapezoidal shaping. The energy resolutions of the 662 keV peak are shown in Figure 8.
It can be seen that the energy resolution deteriorates with the decrease of tWidth. However, even if tWidth is reduced to 100 ns when ε′ is used for amplitude correction, the energy resolution worsens only to 10.6% (tTop = 10 ns). Thus, this temperature correction method can work well for high count rate.
4. Discussion
The R2 values of the exponent-double exponents sum convolution models fitted to the average pulse at different temperatures were both greater than 0.9980, showing the best performance among the compared models. However, there was a certain deviation between the model and the real response. The high R2 values was partly due to the smoothness of the average pulses, and the fitting residual mainly reflected the model error. In fact, it can be seen from Figure 5 that there are certain differences between ε and ε’ for different trapezoidal parameters, which is caused by model error. The actual scintillator luminescence process is very complicated [17,18,19], which is difficult to be described by simple mathematical functions. The pulse models used in practice are simplified models for practical purposes. In principle, a more complex model can be used to improve the accuracy of fitting, but it will increase the difficulty of fitting and subsequent deconvolution. From the practical point of view, the complexity and accuracy of the model should be considered comprehensively. In this paper, the exponent-double exponents sum convolution model was selected because of its moderate complexity. Although there was some deviation between the pulse model and the actual response, the consistency of pulse shapes after deconvolution and trapezoidal shaping at different temperatures shown in Figure 4 reflects the effectiveness of this method in pulse shape correction. Compared with previous temperature correction methods [5,6,7,8,9,10,11,12], this method can be used at high count rate due to the correction of pulse shape and adjustable trapezoid width.
After correction by this method, the position drifts of the 662 keV peak at -20℃~50℃ were less than 3 keV (ε’). The sum spectra with the trapezoidal parameters of tWidth = 1000 ns and tTop = 500 ns has a resolution of 6.91%@662 keV(ε’), which verifies the spectral stabilization effectiveness of the proposed method. It should be noted that this result is obtained under ideal conditions: firstly, the pulse model construction and spectral drift evaluation have been all aimed at the 662 keV gamma rays; secondly, constant temperature conditions in the experiment ensure the consistency of temperature in the hole NaI(Tl) crystal and PMT; thirdly, the temperature values used for calculating the model parameters are the same as those used for pulse processing, which avoids the additional errors introduced by model parameters estimation using temperature.
As shown in Figure 8, the energy resolution is related to trapezoid width tWidth and flat-top ratio, which is because trapezoid parameters will affect the SNR of trapezoid pulse. Figure 8 can provide a basic reference for selecting trapezoidal parameters at specific count rate. The energy resolution deteriorates with the decrease of tWidth, which can be interpreted as that the fewer data points are used to calculate the pulse amplitude information with the narrower trapezoidal width. Therefore, a relatively wide tWidth value should be adopted at low count rate, and a smaller tWidth value should be adopted with the increase of count rate in order to reduce the pile-up effect of trapezoidal pulse. When tWidth is small, the energy resolution becomes better with the decrease of the flat-top ratio. Therefore, it is advisable to adopt a smaller flat-top ratio at high count rate. When using ε’ for amplitude correction, even if tWidth is reduced to 100 ns, a energy resolution of 10.60% can still be obtained by adjusting the flat-top ratio, which preliminarily verifies the effectiveness of this method at high count rate. It should be noted that, although the pulse pile-up effect can be reduced by using smaller tWidth at high count rate, the statistical fluctuations inherent in the pulse signals can not be eliminated, which is reflected in the random fluctuation of the baseline on the right side next to the trapezoidal in Figure 4(c) and Figure 4(d), and it will reduce the SNR of trapezoid pulse. Therefore, the actual energy resolution at high count rate will be worse than that shown in Figure 8.
In this paper, it was assumed that the pulse shape of NaI(Tl) shoud be independent of energy, and only one energy point of 137Cs 662 keV was verified. The consistency of the Compton edge in the energy spectra at different temperatures in Figure. 6(d) can provide partial verification for the validity of the spectrum stabilization at other energy points. Due to the nonlinear energy response of NaI(Tl) crystal [18,19], the hypothesis that the pulse shape is independent of energy can not be perfectly satisfied in practice, so the effectiveness of this method at other energy points needs to be further verified.
In addition, in the amplitude correction step, only amplitude changes of trapezoidal pulse caused by NaI(Tl) response and temperature effect of PMT gain were considered. The gain changes caused by magnetic effect and count rate effect of PMT still need to be stabilized by magnetic shielding and voltage divider circuit design. Moreover, the amplitude correction step is independent of the steps of deconvolution and trapezoidal shaping. Therefore, the amplitude correction step can also be replaced by traditional spectral stabilization methods.
5. Conclusions
This paper proposed a temperature correction method for NaI(Tl) spectrometers, which is divided into three steps: deconvolution, trapezoidal shaping and amplitude correction. This method can shape the pulses at different temperatures into regular trapezoidal pulses with the same tWidth and tTop, and the amplitude HT of the trapezoidal pulse can be corrected to be equal to the pulse area A0 at the reference temperature (20℃). Compared with the existing spectrum stabilization methods based on adjusting the PMT high voltage or amplifier gain, the proposed method process scintillation pulses rather than energy spectrum. This method can be used for field applications, including high counting rate occasion. Through adjusting the trapezoidal parameters, an acceptable energy resolution can be obtained. Results show that the proposed method can effectively correct the temperature response of NaI(Tl) detectors, and the position of 662 keV peak changes less than 3 keV with temperature ranging from -20℃ to 50℃. The trapezoidal parameters can affect the final energy resolution, but even when the trapezoidal pulse width is reduced to 100 ns, energy resolution of 10.60% can still be ensured.
In this paper, the temperature values of the thermostatic chamber are directly used in the deconvolution operation. In practical application, the temperature can be obtained by a temperature sensor or estimated by the method of pulse fitting or pulse shape parameter. It should be noted that the correction in this paper is only for temperature effect of the scintillator and the PMT. Other factors affecting PMT gain and the instability of high voltage and amplifier gain are not considered. These problems can be easily solved by replacing the amplitude correction step in this method with the traditional spectrum stabilization technique.
Although a NaI(Tl) detector is used in this paper, this method can be applied to other scintillation detectors, and the trapezoidal filter can also be replaced by an optimum filter to achieve better energy resolution. Although the off-line pulse processing method is used in this paper, we are going to implement it in FPGA in the future.
Author Contributions
Jianming Xie: Conceptualization, Methodology, Validation, Investigation, Original draft preparation. Liu Yang: Conceptualization, Review and editing. Jinglun Li: Methodology. Yuzhong Zhang: Software. Sheng Qi: Investigation, Review and editing. Wenzhuo Chen: Review and editing. Ye Chen: Software. Hang Xu: Review and editing. Wuyun Xiao: Conceptualization, Methodology, Review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors want to thank the researchers in the State Key Laboratory of NBC Protection for Civilian, for their help in the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gilmore, G. Practical gamma-ray spectroscopy. Chichester: John Wiley & Sons, 2008, 207.
- Schweitzer, J.S.; Ziehl, W. Temperature dependence of NaI(Tl) decay constant. IEEE Transactions on Nuclear Science 1983, 30, 380–382. [Google Scholar] [CrossRef]
- Moszyński, M.; Nassalski, A.; Syntfeld-Każuch, A.; Szczęśniak, T.; Czarnacki, W.; Wolski, D.; Stein, J. Temperature dependences of LaBr3 (Ce), LaCl3 (Ce) and NaI(Tl) scintillators. Nuclear Inst. and Methods in Physics Research, A, 2006, 568, 739–751. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation detection and measurement. Hoboken: John Wiley & Sons, 2010, 241.
- Dudley, R.A.; Scarpatetti, R. Ṡtabilization of a gamma scintillator spectrometer against zero and gain drifts. Nucl. Instrum. Methods 1963, 25, 297–313. [Google Scholar] [CrossRef]
- Patwardhan, P.K. Spectrum stabilization with variable reactance gain control. Nucl. Instrum. Methods 1964, 31, 169–172. [Google Scholar] [CrossRef]
- Stromswold, D.C.; Meisner, J.E. Gamma-ray spectrum stabilization in a borehole probe using a light emitting diode. IEEE Trans. Nucl. Sci. 1979, 26, 395–397. [Google Scholar] [CrossRef]
- Casanovas, R.; Morant, J.J.; Salvadó, M. Temperature peak-shift correction methods for NaI(Tl) and LaBr 3(Ce) gamma-ray spectrum stabilisation. Radiat. Meas. 2012, 47, 588–595. [Google Scholar] [CrossRef]
- Tsankov, L.T.; Mitev, M.G. A simple method for stabilization of arbitrary spectra, in: Proceedings of the Sixteen International Scientific and Applied Science Conference ELECTRONICS ET. Sozopol, 2007, pp. 3–8.
- Ye Chen, Jinglun Li, Yuzhong Zhang, Wuyun Xiao. Gamma spectrum stabilization method based on nonlinear least squares optimization. Applied Radiation and Isotopes 2021, 169, 109515, ISSN 0969–8043.
- Pommé, S.; Sibbens, G. Concept for an off-line gain stabilisation method. Appl. Radiat. Isot. 2004, 60, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Pausch, Guntram & Stein, Juergen & Kreuels, Achim & Lueck, F & Teofilov, Nikolai. Multifunctional application of pulse width analysis in a LED-stabilized digital NaI(Tl) gamma spectrometer. 2005, 1, 19–24. [CrossRef]
- Stein, Jurgen; et al. Radiation detector signal processing using sampling kernels without bandlimiting constraints. 2007 IEEE Nuclear Science Symposium Conference Record. Vol. 1. IEEE, 2007.
- Wuyun Xiao, Abi T. Farsoni, Haori Yang. A new pulse model for NaI(Tl) detection systems. Nuclear Inst. and Methods in Physics Research, A, 2014, 763, 170–173. [CrossRef]
- Radeka, V. Trapezoidal filtering of signals from large germanium detectors at high rates. Nuclear Instruments and Methods 1972, 99, 525–539. [Google Scholar] [CrossRef]
- Wuyun Xiao, Abi T. Farsoni, Haori Yang. Model-based pulse deconvolution method for NaI(Tl) detectors. Nuclear Inst. and Methods in Physics Research A 2015, 769. [Google Scholar]
- Alexandrov, B. S.; Ianakiev, K.D.; Littlewood, P.B. Branching transport model of NaI (Tl) alkali-halide scintillator. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detectors and Associated Equipment 2008, 586, 432–438. [Google Scholar] [CrossRef]
- Payne, S.A.; Moses, W.W.; Sheets, S.; et al. Nonproportionality of scintillator detectors: Theory and experiment. II. IEEE Transactions on Nuclear Science 2011, 58, 3392–3402. [Google Scholar] [CrossRef]
- Khodyuk, I.V.; Dorenbos, P. Trends and patterns of scintillator nonproportionality. IEEE Transactions on Nuclear Science 2012, 59, 3320–3331. [Google Scholar] [CrossRef]
Figure 1.
Schematic diagram of the proposed method.

Figure 2.
Average pulse of 662 keV at different temperatures.

Figure 3.
Comparison of R2 values of average pulse fitted by different models.

Figure 4.
Actual pulses from 662 keV at different temperatures and their processing results(a) original pulse; (b) deconvolution pulse; (c) trapezoidal pulse (tWidth = 200 ns, tTop = 100 ns); (d) trapezoidal pulse (tWidth = 1000 ns, tTop =500 ns).
Figure 4.
Actual pulses from 662 keV at different temperatures and their processing results(a) original pulse; (b) deconvolution pulse; (c) trapezoidal pulse (tWidth = 200 ns, tTop = 100 ns); (d) trapezoidal pulse (tWidth = 1000 ns, tTop =500 ns).

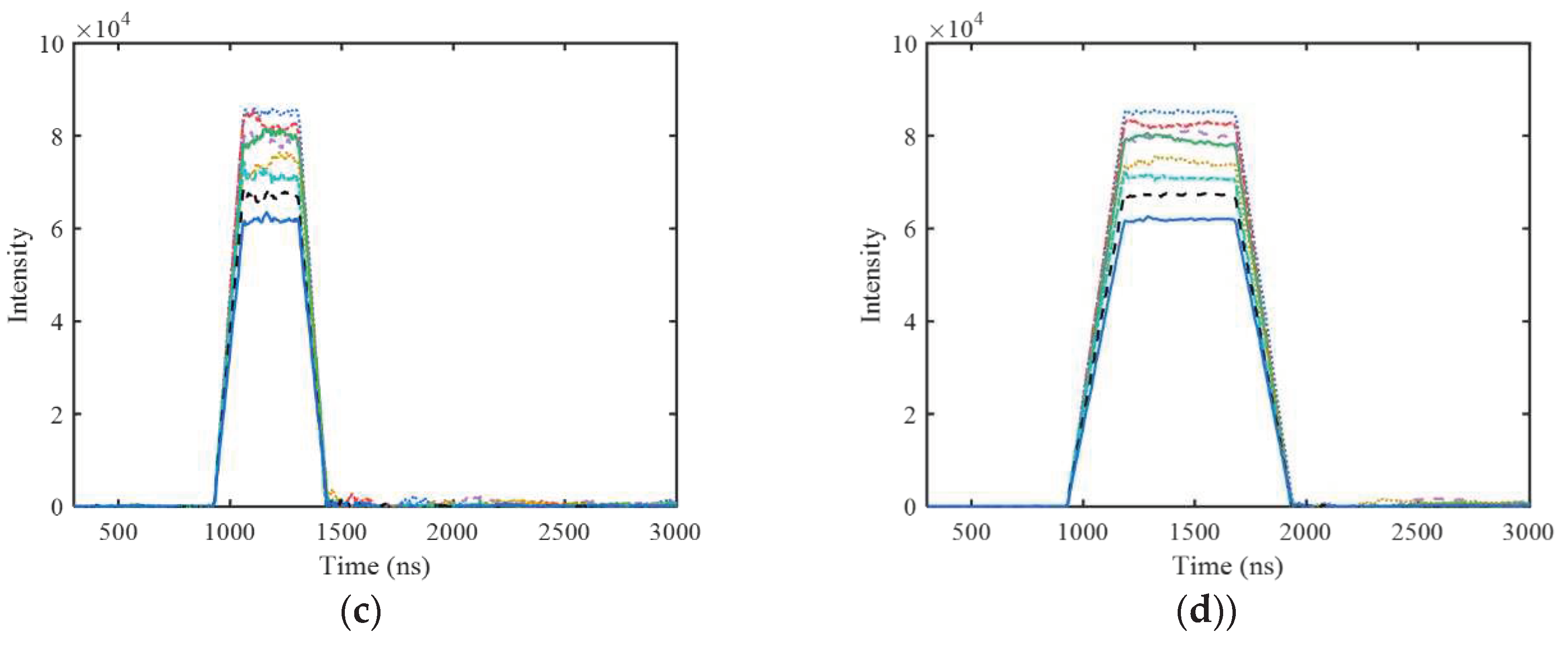
Figure 5.
Amplitude correction factors at different temperatures. Trapezoid parameters 1: tWidth = 500 ns, tTop = 100 ns; Trapezoid parameters 2: tWidth = 500 ns, tTop = 250 ns; Trapezoid parameters 3: tWidth = 1000 ns, tTop = 200 ns; Trapezoid parameters 4: tWidth = 1000 ns, tTop = 500 ns.
Figure 5.
Amplitude correction factors at different temperatures. Trapezoid parameters 1: tWidth = 500 ns, tTop = 100 ns; Trapezoid parameters 2: tWidth = 500 ns, tTop = 250 ns; Trapezoid parameters 3: tWidth = 1000 ns, tTop = 200 ns; Trapezoid parameters 4: tWidth = 1000 ns, tTop = 500 ns.
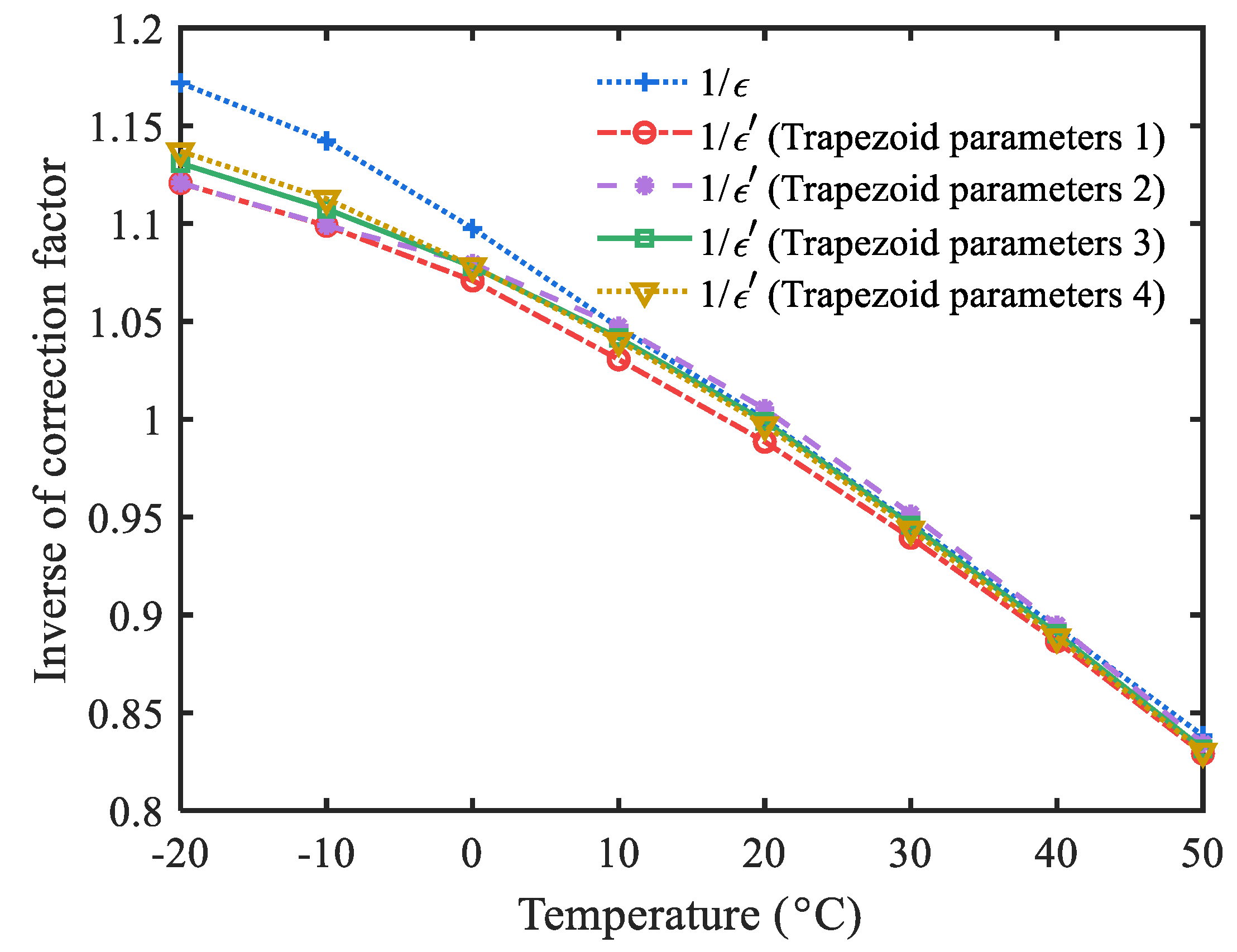
Figure 6.
Spectra got with different methods at different temperatures. (a) 1000 ns gated integration; (b) 7000 ns gated integration; (c) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε); (d) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε′).
Figure 6.
Spectra got with different methods at different temperatures. (a) 1000 ns gated integration; (b) 7000 ns gated integration; (c) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε); (d) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε′).
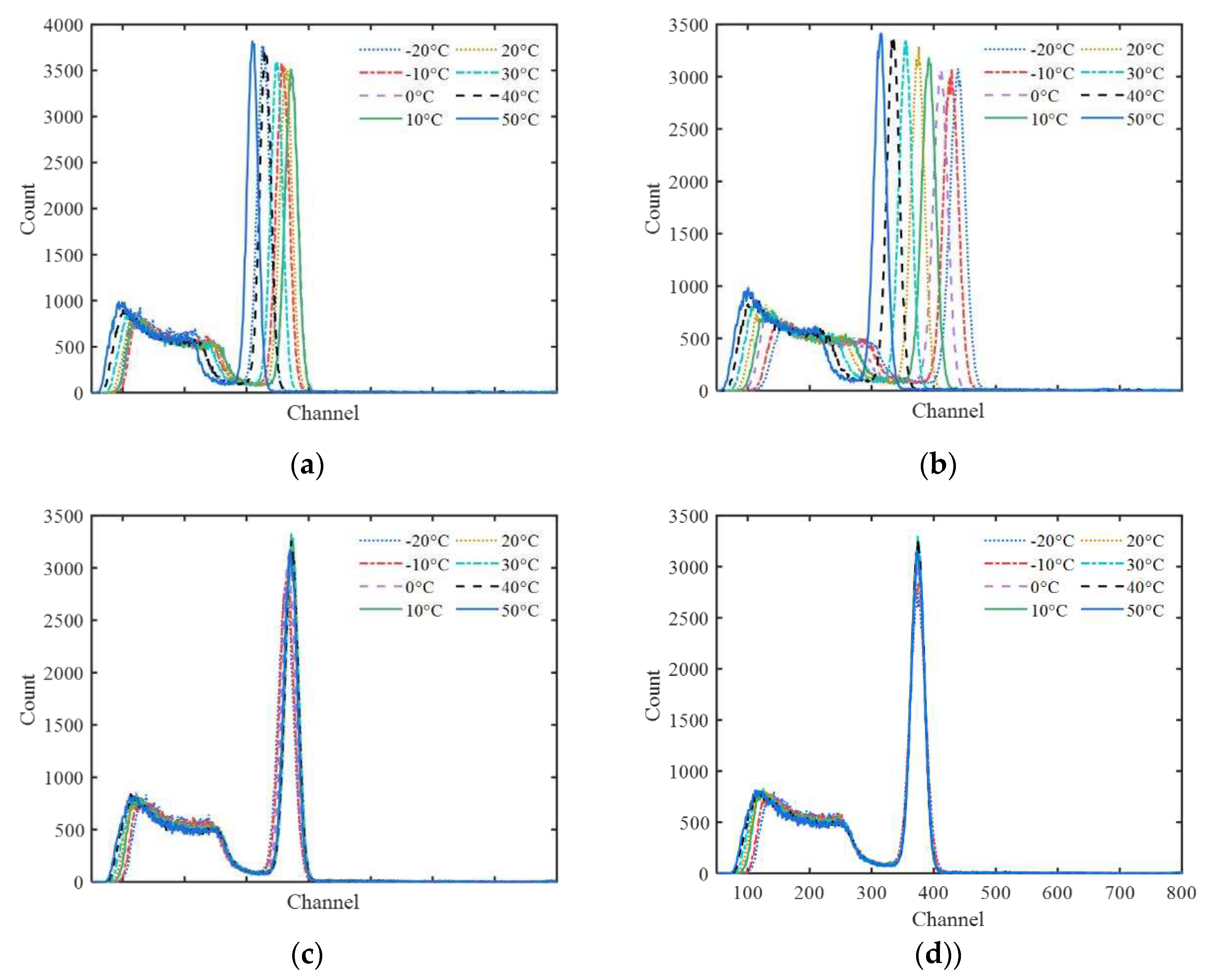
Figure 7.
Sum spectra obtained by different processing methods. (a) 1000 ns gated integration; (b) 7000 ns gated integration; (c) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε); (d) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε′).
Figure 7.
Sum spectra obtained by different processing methods. (a) 1000 ns gated integration; (b) 7000 ns gated integration; (c) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε); (d) The proposed method (tWidth = 1000 ns, tTop = 500 ns, ε′).

Figure 8.
The 662 keV resolution of sum spectra with different correction factors and trapezoidal parameters (a) Amplitude corrected by ε; (b) Amplitude corrected by ε′.
Figure 8.
The 662 keV resolution of sum spectra with different correction factors and trapezoidal parameters (a) Amplitude corrected by ε; (b) Amplitude corrected by ε′.

Table 1.
Parameter fit results of exponent-double exponent sum convolution model.
| Temperature/℃ | A | τ0/ns | τ1/ns | τ2/ns | φ | t0/ns |
|---|---|---|---|---|---|---|
| -20 | 3.382×105 | 9.784 | 160.8 | 842.9 | 0.2682 | 933.3 |
| -10 | 3.302×105 | 9.343 | 218.8 | 603.0 | 0.3202 | 933.3 |
| 0 | 3.194×105 | 11.67 | 271.2 | 404.9 | 0.3778 | 937.4 |
| 10 | 3.059×105 | 18.05 | 281.1 | 281.3 | 0.8297 | 930.6 |
| 20 | 2.935×105 | 23.05 | 236.2 | 236.4 | 0.8120 | 929.4 |
| 30 | 2.785×105 | 25.34 | 199.7 | 200.0 | 0.9993 | 929.3 |
| 40 | 2.625×105 | 25.24 | 174.0 | 200.0 | 1.000 | 929.4 |
| 50 | 2.453×105 | 23.93 | 155.9 | 200.0 | 1.000 | 929.7 |
Table 2.
Fit results of ε and ε’ for different trapezoidal parameters.
| a0 | a1 | a2 | R2 | ||
|---|---|---|---|---|---|
| ε | -1.537×10-5 | -4.398×10-3 | 1.095 | 0.9993 | |
| ε′ | tWidth = 500 ns, tTop = 100 ns | -2.928×10-5 | -3.335×10-3 | 1.068 | 0.9997 |
| tWidth = 500 ns, tTop = 250 ns | -4.033×10-5 | -2.900×10-3 | 1.078 | 0.9993 | |
| tWidth = 1000 ns, tTop = 200 ns | -3.214×10-5 | -3.345×10-3 | 1.077 | 0.9998 | |
| tWidth = 1000 ns, tTop = 500 ns | -2.861×10-5 | -3.563×10-3 | 1.078 | 0.9998 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution
Jianming Xie
et al.
,
2023
Methodological and Conceptual Progresses in Studies on the Latent Tracks in PADC
Tomoya Yamauchi
et al.
,
2021
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








