Preprint
Article
Deeper Flow Behavior Explanation of Temperature Effects on the Fluid Dynamic inside a Tundish
Altmetrics
Downloads
101
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 December 2023
Posted:
11 December 2023
You are already at the latest version
Alerts
Abstract
The continuous casting tundish is non-isothermal due to heat losses and temperature variation from the inlet stream generating relevant convection forces. This condition is commonly avoided through qualitative fluid dynamic analysis only. This work searches to establish the conditions for which non-isothermal simulations are mandatory or for which isothermal simulations are enough to accurately describe the fluid dynamics inside the tundish by quantifying the buoyant and inertial forces. The mathematical model, simulated by CFD software, considers the Navier-Stokes equations, the realizable k- model for solving the turbulence, and the Lagrangian discrete face to track the inclusion trajectories. The results show that temperature does not significantly impact the volume fraction percentages or the mean residence time results, nevertheless, bigger velocity magnitudes under non-isothermal conditions than in isothermal conditions and noticeable changes in the fluid dynamics between isothermal and non-isothermal cases in all the zones where buoyancy force dominates over inertial forces were observed. Because of the results, it is concluded that isothermal simulations can accurately describe the flow behavior in tundishes when the flow control devices control the fluid dynamic, but the simulation without control devices or with a weak fluid dynamic dependence on the control devices requires non-isothermal simulations.
Keywords:
Subject: Engineering - Metallurgy and Metallurgical Engineering
1. Introduction
The tundish is an essential reactor of the continuous casting machine. Its primordial goal is to feed the mold with steel homogeneous in temperature and chemical composition. Additionally, the tundish tries to minimize the new inclusion generation and improve the inclusion removal, implying that its good operation guarantees high-quality steel production. Focusing on tundish temperature control, the slag layer on the tundish top provides thermal insulation of the molten steel from losing heat with the atmosphere. However, heat losses exist throughout steel contact with the refractory walls, flow control devices, and even more from heat to heat. Because of that, in recent years, more researchers have considered the temperature variable in their simulations [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] versus most previous works, which ignore their effects [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. Both approaches have generated debate about the importance of temperature on the flow patterns among researchers [19,20,21,22,23,24,25,26]. Some assure that temperature effects strongly impact the flow patterns inside the tundish. For example, Miki et al. [19], studying a tundish with one strand and a dam, found a steel temperature drop of five grades inside the tundish, generating notorious changes in the fluid dynamics compared with the isothermal case due to the thermal convection, which also induces a stronger inclusion removal rate for the non-isothermal case. Alizadeth et al. [20], studying a tundish with two strands, turbulence inhibitor, and dams, analyze the RTDs for isothermal and non-isothermal conditions determining that the mixed fraction volume is lower for the isothermal case than the non-isothermal due to the buoyancy force forcing the flow towards the top surface. Sun et al. [21], studying a single strand tundish with turbulence inhibitor, dam, weir, and stopper rod, confirm the results reported by Alizadeth [20] and additionally noted that the RTD-s for both cases have the same tendency, concluding that although the isothermal simulation cannot reflect in detail the flow patterns, they can determine the optimal design for the flow controls. Chaterjee et al. [22], studying a tundish with four strands and an impact pad, found that the flow patterns far from the inlet zone can change drastically in a non-isothermal case. The temperature induces a strong inclusion coupling with the flow, which induces an increment in the removal inclusion rate. Zhu et al. [23] use a four-strand tundish with baffles, finding that control devices can cushion but not eliminate the temperature impact.
In contrast, other researchers affirm that this variable is unimportant, disdaining the temperature effects for considering them insignificant. For example, Morales et al. [24], using a two-strand tundish with a weir, dam, and turbulence inhibitor, determined that the thermal disturbances due to the ladle change modify the fluid dynamics immediately after the input. Still, the flow behaves similarly to an isothermal state after a short period. Using a four-strand tundish, Chattopadhyay et al. [25] found a strong influence of the natural convection if the tundish is empty; however, using an impact pad, the temperature effects on the fluid dynamics and removal rates vanish. Sousa Rocha et al. [26], using a two-strand tundish with different configurations for the flow control devices, did not find substantial differences between the isothermal and non-isothermal cases.
The previously mentioned works studied and clarified the differences and similitudes between isothermal and non-isothermal simulations on the steel flow patterns in the tundish. Nevertheless, all these efforts are qualitative, and it is still undetermined if the temperature does or does not substantially affect the flow patterns and if the flow control devices can or cannot vanish the temperature effects on the fluid dynamics. Therefore, this work aims to establish the conditions for which non-isothermal simulations are mandatory or for which isothermal simulations are enough to accurately describe the fluid dynamics inside the tundish by quantifying the buoyant and inertial forces.
2. Materials and Methods
2.1. Mathematical Model Development
The mathematical model considers the equations of mass conservation and the Navier-Stokes equations. To describe the effects of turbulent fluctuations, the realizable k-ε model [46] was employed; moreover, the transport equation for the turbulent kinetic energy (k) and the other for the dissipation rate (ε) introduces additional equations to account for non-isotropic effects providing better accuracy in flows with strong streamline curvature and swirling motion. The Lagrangian discrete phase model was used to predict the inclusion behavior and calculate the phase trajectories. The commercial ANSYS Fluent® CFD code solved the equations simultaneously using the following assumptions and considerations.
2.2. Main Assumptions and Considerations
The system was simulated in three Cartesian coordinates considering isothermal and non-isothermal conditions. The gravity force acts vertically in the incoming flow direction. The typical non-slip conditions apply to the solid surfaces. The molten steel behaves as an incompressible Newtonian fluid. The simulation considers an air zone of 100 mm and a slag zone of 70 mm. The non-isothermal simulation considers a tundish wall of magnesia. The physical properties of steel, slag, air, and magnesia are in Table 1.
The simulations are transient following the next sequence: the isothermal case requires simulating 300s using the implicit formulation and then 60s using the explicit formulation using 0.01s as the time step size to achieve the quasi-steady state. For the non-isothermal case, the base was the previously described isothermal case using a time step of 0.005, turning on the temperature. The inlet and outlet temperatures were 1800K and 1793K, respectively. Heat losses from the bottom, walls, and flow control devices are in Table 2. Reaching the quasi-steady state in the explicit formulation for the non-isothermal conditions after 32 minutes. All simulations' convergence criterion requires residuals smaller than 10-4. All the images and calculations for the isothermal and non-isothermal cases were taken once the simulations achieved the quasi-steady state. The inlet and outlet velocities were calculated based on the volumetric flow of 297.8 l/min.
Once isothermal and non-isothermal cases achieve the quasi-steady state, 2000 inclusions of a single size 1, 20, 40, 60, 80, 100, 130, 150, 180, and 200μm were fed as an impulse at the ladle shroud surface entry. The Lagrangian Model calculates the inclusions' trajectories until they are trapped at the free surface of the tundish or until the inclusions reach the outlet. The fed inclusions are spherical solid particles with alumina properties (density = 3960 kg/m3) and without interaction among them.
2.3. Mathematical Model Equations
The mathematical model is based on the Navier Stokes equations for incompressible flows. The model solves simultaneously the following continuity equation and momentum conservation equations:
Where is the fluid density. is the fluid velocity, is the pressure, is the effective viscosity given by , with the fluid viscosity and the turbulent viscosity, is the coefficient of volumetric thermal expansion, is the temperature, and is the gravity acceleration.
2.3.1. The Standard k-ε realizable Turbulence Model
The realizable k-ε proposed by Shih et al. [46] model contains a new formulation for the turbulent viscosity and the dissipation rate ε.
Where Cμ is no longer a constant.
This model is more accurate for flows involving rotation. Boundary layers under strong adverse pressure gradients, separation, and recirculation.
The equations that describe the transport of the turbulent energy k and dissipation rate ε are given by:
In this equation , and . represents the generation of turbulence kinetic energy due to the mean velocity gradients. is the generation of turbulence kinetic energy due to buoyancy represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate, and are constants, and are the turbulent Prandtl numbers. and are user-defined source terms.
2.3.2. The Lagrangian Discrete Phase Model
The Lagrangian model [47] solves a transport equation for each inclusion as it travels inside the flow field by integrating the force balance acting on the particle. This force balance is as follows:
The drag force per unit particle mass tends to induce the inclusion to follow the steel flow trajectory. The buoyant () and gravity forces (), act only in the vertical direction, inducing ascending or descending moves. The term () corresponds to the Saffman force, which promotes radial and lifting effects. The virtual mass force (), quantifies the required force to accelerate the fluid around the inclusions. The last force in Eq. (6) is the gradient force generated by the pressure differences from one point to another.
2.4. Numerical Procedure
The geometries, dimensions and model mesh of the tundish and the flow control devices are in Figure 1, Figure 2 and Figure 3. The discretization of the governing equations uses the finite volume technique through the commercial CFD code. The non-linear momentum equations were linearized using the implicit approach, and the discretization requires the Second Order Upwind scheme. The pressure interpolations use the PRESTO scheme and the PISO algorithm for the pressure-velocity coupling. The volume of fluid (VOF) [47] method models the multiphase steel-slag-air system.
2.5. Physical model
Physical modeling is a powerful tool for understanding and studying the fluid dynamics occurring inside industrial tundishes with the advantage of small costs. In the water physical modeling, the most common scale condition is the Froude similarity criterion, where the ratio between inertial to gravitational forces in the model and prototype must be equal to:
V, L are the characteristic velocity and length, is the fluid density. Froude similarity criterion provides relationships between the variables in the scaled water model and prototype isothermal tundish. Having these relationships, if the variable values are known in the water model, the prototype variable values can be predicted. Some of these relationships, for example, for the length, volumetric flow rate, volume, velocity, and time, are:
where λ is the scale factor.
3. Results and discussion
3.1. Mathematical model validation
The water modeling made of transparent 12 mm thick plastic sheets employs a 1:3 scaled model obeying the Froude criterion. Frames from a recorded video of an impulse injection tracer are used to study and analyze the fluid dynamics inside this water model under isothermal conditions. At the same time, predictions of the impulse injection tracer behavior by mathematical modeling are obtained considering again isothermal conditions in a full-scale model. Figure 4 shows the results of tracer behavior for the physical modeling at three representative times (3, 22, and 35s) and its corresponding times for the mathematical model (5.2, 38, and 61s) following the equation . Figure 4a,b show that the tracer does not enter the tundish homogenously, having a faster entry for the right side. Once the tracer impacts with the turbulence inhibitor, it moves upward until reaching the bath level, later shows two preferential streams; the first moves to the right side, crashing with the lateral tundish wall to continue a descending movement, see Figure 4c,d; The second stream tracer remains moving parallel to the top surface and starts to fall at the half distance between the ladle shroud entry and the right lateral tundish wall, at the same time another small tracer stream moves close to the tundish floor, see Figure 4e,f. According to the previous results, it can be considered that the physical and the mathematical models have a good agreement, and consequently, the mathematical model is validated.
To demonstrate if a scaled mathematical model can accurately predict the flow patterns and volume fractions as a full-scale model, a 1:3 mathematical model was also simulated. Since the full-scale mathematical model is validated, the following comparison will be done between only the mathematical results. Figure 5a,b exhibit the velocity vector fields in a longitudinal plane at the ladle shroud entry axis. The velocity range is from 0 to 0.023 for the reduced scale case and from 0 to 0.04m/s, satisfying the expected relation . The similarities between both cases are evident, showing a flow recirculation on the left side of the ladle shroud, a short circuit on the right side, and a second recirculation between the short-circuit position and the tundish floor. Consequently, both mathematical results predict qualitatively the same flow patterns. Nevertheless, it is crucial to verify if the quantifiable parameters also agree. Then, Figure 5c contains the RTDs curves for both cases, and Table 3 has the piston, mixed, and dead volume fractions percentages and the non-dimensional residence time for both cases. From Figure 5c is appreciable the same tendency of both curves. The residence time for the scaled case is 222 s and 372 s for the full-scale case, which satisfy the relation with a difference of 3.7 %. The reported values in Table 3 are close for both cases, with a maxima difference of 4% for the mixed volume fraction. Therefore, the above-discussed results demonstrate that the scaled and full-scale models predict the same flow patterns, volume fractions, and residence time, with less than 4% differences following the Froude criteria. Consequently, both mathematical models are equally validated, and any can predict the flow patterns of the physical model. The present research considers a full-scale model for further analysis since the simulation will include the temperature variable.
3.2. Comparison between isothermal and non-isothermal cases
To establish the effect of the temperature on the tundish flow patterns, Figure 6 shows tracer concentration contours, for three representative times, to contrast the tracer behavior for the isothermal Figure 6a–c and the non-isothermal (Figure 6d–f) cases. Figure 6a,d show that the tracer behaves similarly in the entry zone for both cases, noting that the flow in the upper right side of the tundish presents a slightly longer trajectory for the non-isothermal case. However, comparing Figure 6b,c against Figure 6e,f, the tracer shows a notorious difference in its flow behavior at the top tundish since, for the non-isothermal case, the flow tends to move near the bath level for a longer distance; while, for the isothermal case, the tracer presents the same stream with a descending trajectory. Looking for a deeper analysis of the flow patterns, Figure 7 shows the fixed velocity vector fields in three planes: a longitudinal plane at the center of the ladle shroud, a longitudinal plane at the exit, and a horizontal plane at the bath level position.
These figures show substantial differences between both cases. For example, the short-circuit previously mentioned in the isothermal case disappears in the non-isothermal case, and the recirculation observed on the right side of the ladle shroud remains in both cases but with different positions and intensities. Also, the non-isothermal case increases the velocity magnitudes for all the planes, being more evident at the bath-level plane. To explain the detected velocity increment requires the Maxwell-Boltzmann velocity distribution function, which is:
Where k is the Boltzmann constant, m is the mass particle, T is the temperature and f(v) is a probability distribution function. The function f(v) indicates the probability of finding a particle with velocity between v to v + dv. Spherical coordinates will be used to find the expression that lets to calculate its value,
Then, after its integration the Eq. 9 becomes:
By choosing two arbitrary temperatures, , and plotting their corresponding f(v) function in Figure 8, it is possible to understand the effect of the temperature on the velocity distribution function. This figure demonstrates that for the higher temperature T2, the curve flattens out, the maximum value of the curve diminishes, the maximum value shifts to the left, and the curve becomes narrower in contrast with the curve of T1. The behavior of this probability distribution function indicates that flows with higher temperatures will have a range of higher velocities. This asseveration applies for the non-isothermal simulation, which will induce that the fluid dynamics present velocity variations because of temperature gradients, being, on average, faster for the hot streams and slower for cold ones; such velocity variations will not be present in the isothermal case since there are not temperature gradients. Following this analysis and for associating velocity increments observed in the non-isothermal case with the previous discussion, it is necessary to study the temperature gradients in the tundish. Figure 9 shows temperature and buoyancy magnitude forces contours. This figure shows that higher temperatures exist at the entry zone and along the bath level. The high velocities at the entry are because of the entry jet. Compared with the isothermal case, the velocities increment observed at the bath level follows the Maxwell-Boltzmann velocity distribution function explanation.
Although the Maxwell-Boltzmann velocity distribution function explains velocity magnitude variations between isothermal and non-isothermal models, it cannot explain why the short-circuit disappears under non-isothermal conditions. The buoyancy and inertial forces are studied since these forces are associated with the parameters of temperature and velocity, respectively, to analyze this point.
The buoyancy force depends on temperature variations inside the tundish, and consequently, it only applies to the non-isothermal case and is given by:
Where β is the thermal fluid expansion that arises due to the differences in the fluid density inside the tundish
Then, given the strong dependency of the buoyancy force on the temperature gradients, the zones that exhibit higher temperature gradients will produce higher buoyancy force values. The results indicate that the main effect of the buoyancy forces occurs in zones near the walls, being less significant in the rest of the tundish, especially at the entry zone. Furthermore, inertial force is another essential force to consider acting in the flow. The inertial force magnitude is in Figure 10a–c for the isothermal case and in Figure 10d–f for the non-isothermal case. As expected, these figures reflect that inertial force magnitudes are meaningful in the entire tundish. However, the non-isothermal case has more zones where the inertial forces act with higher values than the isothermal case for all the shown planes, especially at the bath level.
To observe which of the two analyzed forces dominate in each region of the tundish, the Richarson Number (Tu) will be employed. This number defines the ratio of buoyancy force and the inertial force as follows:
Then, if Tu tends to zero, the inertial force is predominant over the buoyancy force, and it is opposite when the ratio is higher than one. Figure 11 shows the contours of the Tu values for the non-isothermal case in the three analyzed planes. The results show that the inertial force dominates over the buoyancy force in the entry zone, around the ladle shroud at the bath level, and very close to the outlet; in contrast, buoyancy force dominates in the detected recirculation zones (points ① and ②) and dead flow zones (points ③, ④, and ⑤). It is crucial to notice that zones where Tu tends to zero correspond to zones with less appreciable flow pattern changes between isothermal and non-isothermal cases.
Considering the above discussion, from Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the flow variations observed between the isothermal and non-isothermal cases have now support. The upward stream flow reaching the bath surface from the turbulence inhibitor has a higher temperature than the rest of the bulk flow. This hotter flow must follow the Maxwell-Boltzmann velocity distribution function, which, together with the buoyancy forces acting upwards below this stream, induces the following changes: 1) at the left ladle shroud side, the recirculation moves upward with an increment in the flow velocity around it; 2) at the right ladle shroud side, the mainstream, moving parallel to the bath level towards the right tundish wall and traveling near the metal-slag interphase, has higher velocity, which reaches a longer distance than in the isothermal case. The second implication forces the short circuit to disappear, moving the recirculation below it toward the right tundish side. These changes are even when the temperature variations inside the tundish are as modest as 3K.
Until this point, the fluid dynamic changes between both cases have been analyzed and explained; however, it is necessary to determine their effect on variables such as volume fractions and inclusion removal rate quantitatively.
Figure 12 shows the RTD curves for both cases. The figure reveals that the curves present similarities in the first appearance of the tracer, θmin, and when the tracer's maximum concentration occurs, θmax. However, it is noticeable that the non-isothermal curve is the highest and slightly thinner than the isothermal one. These differences are quantifiable by the volume fraction calculation presented in Table 4.
The results indicate that the volume fraction percentages are similar with a flow moving mainly as a mixed flow. In addition, there is an increment in the piston flow of 1%, a decrement in the mixed flow of 4%, an increment in the dead volume of 3%, and a decrement in the non-dimensional residence time of 2.1% for the non-isothermal case concerning the isothermal case.
Now, doing an inclusion analysis, Figure 13a presents the inclusion removal percentage for the isothermal and non-isothermal cases. The results show that the removed inclusions in a range of 1 to 40μm reach at least 35%, and the removal percentage for inclusions bigger than 130μm is almost 100% for both cases. The non-isothermal case presents approximately 5% more inclusion removal percentages than the isothermal case for inclusions ranging from 1 to 60μm; this was the most notorious difference between both curves. A sample of such distribution for both cases considering an inclusion size of 40μm is analyzed to observe if the flow affected by the temperature effects modifies the inclusion removal distribution at the steel-slag interface, see Figure 13b. These figures show that the preferential removal zone is around the ladle shroud, which is a consequence of the strong effect of the turbulence inhibitor redirecting the flow to the position of the bath level. Then, the removed inclusions diminish in the zones towards the outlet direction; the previous observations apply for both cases. To corroborate and quantify that there is no significative influence of the temperature on the removed inclusion distribution for all inclusion sizes, Figure 14 shows the inclusion removal percentage calculated for each inclusion size distributed for zones at the bath level for isothermal and non-isothermal cases. The results of Figure 14 indicate that the inclusion removal distribution is similar for all the inclusion sizes regarding the non-isothermal or isothermal conditions. Therefore, the flow velocity increment in the non-isothermal case and the short circuit in the isothermal case do not significantly impact the inclusion removal rate or its distribution at the bath level.
4. Conclusions
This work research the temperature effect on the fluid patterns and inclusion removal rates in a continuous casting tundish using mathematical simulation. From the previously discussed results, the following conclusions are drawn:
- (1)
- The quantification of the differences between the results of 1:3 scaled and full-scale models, which have a maxima difference of 4% on the volume fractions percent and residence time, demonstrate that scaled and full-scale models can be used reliably to predict the flow patterns of an isothermal physical model following the Froude criteria.
- (2)
- Temperature gradients inside the tundish induce variations in the flow velocity magnitude; if the stream has a higher temperature than its surrounding flow, its velocity will increase because of the Maxwell-Boltzmann velocity distribution function; this supports why hot streams, e.g., at the bath level, under non-isothermal conditions, have bigger velocity magnitudes than the same streams but under isothermal conditions.
- (3)
- The quantification of the ratio between inertial and buoyancy forces demonstrates that the inertial forces dominate over buoyancy forces at the entry zone because turbulence inhibitor strongly controls the fluid dynamics in such area. In contrast, the buoyancy forces take more relevance than inertial forces in the recirculation and dead flow zones, inducing noticeable changes in the fluid dynamics between isothermal and non-isothermal cases far from the entry zone.
- (4)
- Although the temperature induces substantial fluid dynamic changes between analyzed cases, this variable does not significantly impact the volume fraction percentages or the mean residence time results, and it only increases the inclusion removal percentage by 5% for the non-isothermal case.
- (5)
- The effect of the temperature on the flow patterns is not significant when the flow control devices strongly rule the fluid dynamics; nevertheless, when the flow control devices effects are not dominant, the temperature takes substantial importance by the buoyancy forces and the increment of flow velocity because the Maxwell Boltzmann velocity distribution function changing the fluid dynamics in comparison with the obtained from the isothermal conditions. Consequently, isothermal simulations can accurately describe the flow behavior in tundishes where its flow control devices control the fluid dynamic. However, the simulation of tundishes without control devices or with a weak fluid dynamic dependence on the control devices requires non-isothermal simulations.
Author Contributions
“Conceptualization, R.D. Morales and J. de J. Barreto; methodology, Enif Gutierrez; software, Enif Gutierrez and Saul Garcia-Hernandez; validation, R.D. Morales and Enif Gutierrez; formal analysis, Enif Gutierrez and Saul Garcia-Hernandez; investigation, Enif Gutierrez; resources, Enif Gutierrez and R.D. Morales; data curation, Enif Gutierrez; writing—original draft preparation, Enif Gutierrez and Saul Garcia-Hernandez; writing—review and editing, Enif Gutierrez, Saul Garcia-Hernandez, and J. de J. Barreto; visualization, Enif Gutierrez; supervision, R.D. Morales; project administration, Enif Gutierrez. All authors have read and agreed to the published version of the manuscript.”
Acknowledgments
The authors thank TecNM-ITM and SNI institutions for their permanent support to the Academic Research Group.
Conflicts of Interest
“The authors declare no conflict of interest.”
References
- D. Sheng and P. Jönsson. Effect of Thermal Buoyancy on Fluid Flow and Residence-Time Distribution in a Single-Strand Tundish, Materials, 2021, Volume 14, pp. 1-20. [CrossRef]
- Q. Wang, Y. Liu, A. Huang, W. Yan, H. Gu and G. Li. CFD Investigation of Effect of Multi-hole Ceramic Filter on Inclusion Removal in a Two-Strand Tundish, Metall. Mater. Trans. B, 2020, Volume 51, pp. 276-292. [CrossRef]
- A. Cwudzinski. Physical and mathematical simulation of liquid steel mixing zone in one strand continuous casting tundish, Int. J. Cast. Met. Res., 2017, Volume 30, pp. 50-60. [CrossRef]
- R. Agarwal, M.K Singh, R. Kumar, B. Ghosh and S. Pathak. Extensive Analysis of Multi Strand Billet Caster Tundish Using Numerical Technique, J. Mech., 2019, Volume 9, pp. 29-51. http://doi.org/10.4236/wjm.2019.92003.
- F. Xing, S. Zheng, Z. Liu and M. Zhu. Flow Field, Temperature Field, and Inclusion Removal in a New Induction Heating Tundish with Bent Channels, Metals, 2019, Volume 9, pp. 1-16. [CrossRef]
- O. Delgado Ramirez, E. Torres-Alonso, A. Ramos-Banderas, S. Arreola Villa, C. Hernández Bocanegra and J. Téllez Martínez. Thermal and Fluid-Dynamic Optimization of a Five Strand Asymmetric Delta Shaped Billet Caster Tundish, Steel Res. Int., 2018, Volume 89, pp. 1-10. [CrossRef]
- H. Tang, L. Guo, G. Wu, H. Xiao, H. Yao, and J. Zhang. Hydrodynamic Modeling and Mathematical Simulation on Flow Field and Inclusion Removal in a Seven-Strand Continuous Casting Tundish with Channel Type Induction Heating, Metals, 2018, Volume 8, pp. 1-25. [CrossRef]
- L. Neves and R. Tavares. Analysis of the mathematical model of the gas bubbling curtain injection on the bottom and the walls of a continuous casting tundish, Ironmak. Steelmak., 2017, Volume 44, pp. 559-567. [CrossRef]
- Y. Sahai. Tundish Technology for Casting Clean Steel: A Review, Metall. Mater. Trans. B, 2016, Volume 47B, pp. 2095-2106. [CrossRef]
- Q. Wang, B. Li and F. Tsukihash. Hydrodynamic Problem in Continuous Casting Tundish with Channel Type Induction Heating, ISIJ Int., 2014, Volume 54, pp. 311-320. [CrossRef]
- P. Ni, L. T. I. Jonsson, M. Ersson and P. G. Jönsson. Turbulent Flow Phenomena and Ce2O3 Behavior during a Steel Teeming Process, ISIJ Int., 2013, Volume 53, pp. 792-801. [CrossRef]
- T. Qu, C. Liu, M. Jiang and L. Zu. Numerical Simulation for Effect of Inlet Cooling Rate on Fluid Flow and Temperature Distribution in Tundish, J. Iron Steel Res. Int., 2012, Volume 19, pp. 12-19. [CrossRef]
- H. Ling and L. Zhang. Numerical Simulation of the Growth and Removal of Inclusions in the Molten Steel of a Two-Strand Tundish, JOM, 2013, Volume 65, pp. 1155-1163. [CrossRef]
- V. Singh, S. Ajmani, A. Pal, S. Singh and M. Denys. Single strand continuous caster tundish furniture comparison for optimal performance, Ironmak. Steelmak., 2012, Volume 39, pp. 171-179. [CrossRef]
- A. Braun, M. Warzecha and H. Pfeifer. Numerical and Physical Modeling of Steel Flow in a Two-Strand Tundish for Different Casting Conditions, Metall. Mater Trans. B, 2010, Volume 41B, pp. 549-559. [CrossRef]
- Vargas-Zamora, R. Morales, M. Díaz-Cruz, J. Palafox-Ramos, and L. García Demedices. Heat and mass transfer of a convective-stratified flow in a trough type tundish, Int. J. Heat Mass Transf., 2003, Volume 46, pp. 3029-3039. [CrossRef]
- S. Joo, J. Han and R. Guthrie. Inclusion behavior and heat-transfer phenomena in steelmaking tundish operations: Part II. Mathematical model for liquid steel in tundishes, Metall. Mater Trans. B, 1993, Volume 24B, pp. 767-777. [CrossRef]
- S. Chakraborty and Y. Sahai. Effect of Varying Ladle Stream Temperature on the Melt Flow and Heat Transfer in Continuous Casting Tundishes, ISIJ Int., 1991, Volume 31, pp. 960-967. https://www.jstage.jst.go.jp/article/isijinternational1989/31/9/31_9_960/_pdf.
- Y. Miki and B. Thomas. Modeling of inclusion removal in a tundish, Metall. Mater. Trans. B, 1999, Volume 30B, pp. 639-654. [CrossRef]
- M. Alizadeh and H. Edris. Prediction of RTD Curves for Non-isotherm steel Melt Flows in Continuous Casting Tundish, Proceedings of International Symposium on Liquid Metal Processing and Casting, LMPC September 2007, pp. 167-172.
- H. Sun, B. Yan, J. Zhang. Effect of Thermal Buoyancy Force on the Flow, Temperature Distribution and Residence Time Distribution of Molten Steel in the Slab Casting Tundish, CFD Modeling and Simulation in Materials Processing; The Minerals, Metals, & Materials Society: Pittsburgh, PA, USA, 2012, pp. 327-334. [CrossRef]
- S. Chatterjee and K. Chattopadhyay. Transient steel quality under non-isothermal conditions in a multi-strand billet caster tundish: part II. Effect of a flow-control device, Ironmaking and Steelmaking, 2016, Volume 44, pp. 413-420. [CrossRef]
- M. Zhu, S. Peng, K. Jiang, J. Luo, Y. Zhong and P. Tang. Fluid Flow and Heat Transfer Behaviors under Non-Isothermal Conditions in a Four-Strand Tundish, Metals, 2022, Volume 12, pp. 1-15. [CrossRef]
- R. Morales, S. Lopez-Ramirez, Palafox-Ramos, and D. Zacharias. Mathematical simulation of effects of flow control devices and buoyancy forces on molten steel flow and evolution of output temperatures in tundish, Ironmaking and Steelmaking, 2001, Volume 28, pp. 33-43. [CrossRef]
- K. Chattopadhyay, M. Isac and R. Guthrie. Modelling of Non-isothermal Melt Flows in a Four Strand Delta Shaped Billet Caster Tundish Validated by Water Model Experiments, ISIJ Int., 2012, Volume 52, pp. 2026-2035. http://dx.doi.org/10.2355/isijinternational.52.2026.
- J. de Sousa, E. Barros, F. Marcondes and J. de Castro. Modeling and computational simulation of fluid flow, heat transfer and inclusions trajectories in a tundish of a steel continuous casting machine, Journal of Materials Research and Technology, 2019, Volume 8, pp. 4209-4220. [CrossRef]
- S. Neumann, A. Asad and R. Schwarze. Numerical Simulation of an Industrial-Scale Prototypical Steel Melt Tundish Considering Flow Control and Cleaning Strategies, Adv. Eng. Mater., 2020, Volume 22, pp. 1-11. [CrossRef]
- R. Mishra and D. Mazumdar: Trans. Numerical Analysis of Turbulence Inhibitor Toward Inclusion Separation Efficiency in Tundish, Indian Inst. Met., 2019, Volume 72, pp. 889-989. [CrossRef]
- E. Gutiérrez, S. Garcia-Hernández and J. de J. Barreto. Mathematical Analysis of the Touching Inclusions Parameters at the Tundish Free Surface to Predict More Realistic Inclusion Removal Rates, Steel Res. Int,. 2019, Volume 90, pp. 1-33. [CrossRef]
- E. Gutiérrez, S. Garcia-Hernández and J. de J. Barreto. Mathematical Modeling of Inclusions Deposition at the Upper Tundish Nozzle and the Submerged Entry Nozzle, Steel Res. Int,. 2016, Volume 87, pp. 1-11. [CrossRef]
- E. Gutiérrez, S. Garcia-Hernández and J. de J. Barreto. Mathematical Analysis of the Dynamic Effects on the Deposition of Alumina Inclusions inside the Upper Tundish Nozzle, ISIJ Int., 2016, Volume 56, pp. 1394-1403. [CrossRef]
- H. Lei, Y. Zhao, and D. Geng. Mathematical Model for Cluster-Inclusion’s Collision-Growth in Inclusion Cloud at Continuous Casting Mold, ISIJ Int., 2014, Volume 54, pp. 1629-1637. [CrossRef]
- Z. Liu, B. Li and M. Jiang. Transient Asymmetric Flow and Bubble Transport Inside a Slab Continuous-Casting Mold, Metall. Mater. Trans. B, 2014, Volume 45B, pp. 675-697. [CrossRef]
- Z. Liu, B. Li, M. Jiang and F. Tsukihashi. Euler-Euler-Lagrangian Modeling for Two-Phase Flow and Particle Transport in Continuous Casting Mold, ISIJ Int., 2014, Volume 54, pp. 1314-1323. [CrossRef]
- K. Takahashi, M. Ando, and T. Ishii. Model of Gas Flow Through Porous Refractory Applied to an Upper Tundish Nozzle, ISIJ Int., 2014, Volume 54, pp. 304-405. [CrossRef]
- Z. He, K. Zhou, S. Liu, W. Xiong, and B. Li. Numerical Modeling of the Fluid Flow in Continuous Casting Tundish with Different Control Devices, A. Appl. Anal., 2013, Volume 2013, pp. 1-8. [CrossRef]
- V. Seshadri, C. da Silva, I. da Silva and E. Junior. A Physical Modelling Study Of Inclusion Removal In Tundish Using Inert Gas Curtain, Tecnol. Metal. Mater. Min., 2012, Volume 9, pp. 22-29. http://dx.doi.org/10.4322/tmm.2012.004.
- M. Long, X. Zuo, L. Zhang, and D. Chen. Kinetic Modeling on Nozzle Clogging During Steel Billet Continuous Casting, ISIJ Int., 2010, Volume 50, pp. 712-720. [CrossRef]
- L. Zhong, L. Li, B. Wang, L. Zhang, L. Zhu and Q. Zhang. Fluid flow behaviour in slab continuous casting tundish with different configurations of gas bubbling curtain, Ironmak. Steelmak., 2008, Volume 35, pp. 436-440. [CrossRef]
- A. Ramos-Banderas, R.D Morales, J. de J. Barreto and G. Solorio-Diaz. Modelling Study of Inclusions Removal by Bubble Flotation in the Tundish, Steel Res. Int., 2006, Volume 77, pp. 325-335.
- Q. Yuan, B. Thomas and S. Vanka. Study of transient flow and particle transport in continuous steel caster molds: Part II. Particle transport, Metall. Mater. Trans. B, 2004, Volume 35B, pp. 703-714. [CrossRef]
- Y. Vermeulen, B. Coletti, B. Blanpain, P. Wollants and J. Vleugels. Material Evaluation to Prevent Nozzle Clogging during Continuous Casting of Al Killed Steels, ISIJ Int., 2002, Volume 42, pp. 1234-1240. [CrossRef]
- L. Zhang, S. Taniguchi and K. Cai. Fluid flow and inclusion removal in continuous casting tundish, Metall. Mater. Trans. B, 2000, Volume 31B, pp. 253-266. [CrossRef]
- K. Sasai and Y. Mizukami. Reaction Mechanism between Alumina Graphite Immersion Nozzle and Low Carbon Steel, ISIJ Int., 1994, Volume 34, pp. 802-809. [CrossRef]
- Y. Fukuda, Y. Ueshima and S. Mizoguchi. Mechanism of Alumina Deposition on Alumina Graphite Immersion Nozzle in Continuous Caster, ISIJ Int., 1992, Volume 32, pp. 164-168. [CrossRef]
- T. Shih, W. Liou, A. Shabbir, Z. Yang and J.A. Zhu. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows, Comput. Fluids, 1995, Volume 24, pp. 227-238. [CrossRef]
- ANSYS Inc. FLUENT 12.0, User’s Guide; Centerra Resource Park: Cavendish Court, Lebanon, 2009. https://www.afs.enea.it/project/neptunius/docs/fluent/html/ug/main_pre.htm.
Figure 1.
Geometry of the tundish and flow control devices (mm). a) Upper view, b) frontal view, c) lateral view, d) ladle shroud.
Figure 1.
Geometry of the tundish and flow control devices (mm). a) Upper view, b) frontal view, c) lateral view, d) ladle shroud.
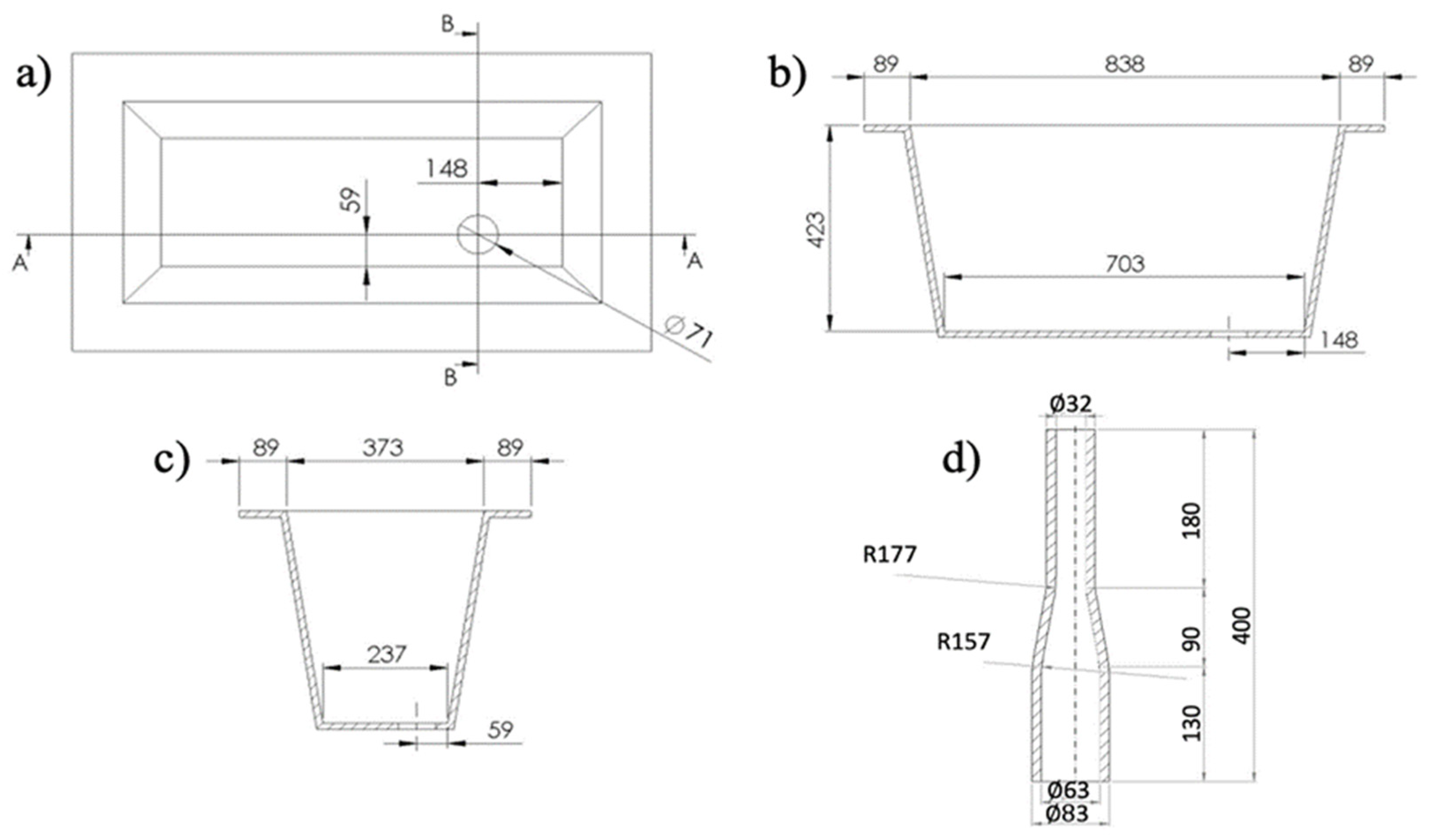
Figure 2.
Geometry and dimensions of the a) turbulence inhibitor, b) vortex killer.

Figure 3.
Tundish mesh, a) general view, close up for the b) ladle shroud, c) turbulence inhibitor, d) vortex killer.
Figure 3.
Tundish mesh, a) general view, close up for the b) ladle shroud, c) turbulence inhibitor, d) vortex killer.

Figure 4.
Comparison of the tracer behavior between the 1:3 scale water model [a), c), e)] and the full-scale mathematical model [b), d), f)].
Figure 4.
Comparison of the tracer behavior between the 1:3 scale water model [a), c), e)] and the full-scale mathematical model [b), d), f)].

Figure 5.
Fixed velocity vectors for a) scaled tundish, b) full-scale tundish, and c) RTD curves for both cases.
Figure 5.
Fixed velocity vectors for a) scaled tundish, b) full-scale tundish, and c) RTD curves for both cases.
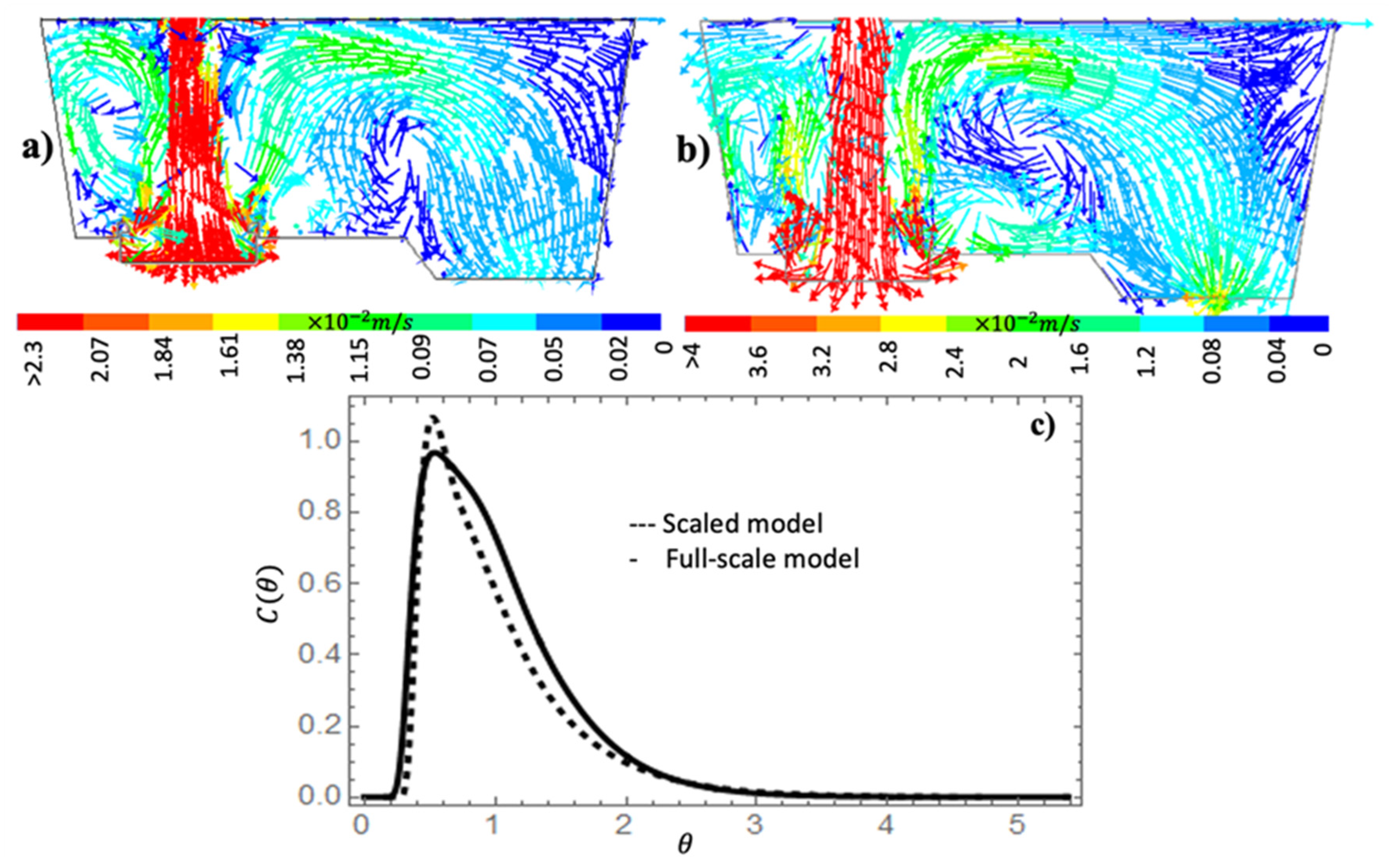
Figure 6.
Tracer concentration contours at the central symmetrical plane of the ladle shroud for the isothermal [a), b), c)] and the non-isothermal [d), e), f)] cases.
Figure 6.
Tracer concentration contours at the central symmetrical plane of the ladle shroud for the isothermal [a), b), c)] and the non-isothermal [d), e), f)] cases.

Figure 7.
Fixed velocity vector fields in three planes [a), b)] center of the ladle shroud, [c), d)] center of the exit, and [e), f)] bath level position.
Figure 7.
Fixed velocity vector fields in three planes [a), b)] center of the ladle shroud, [c), d)] center of the exit, and [e), f)] bath level position.
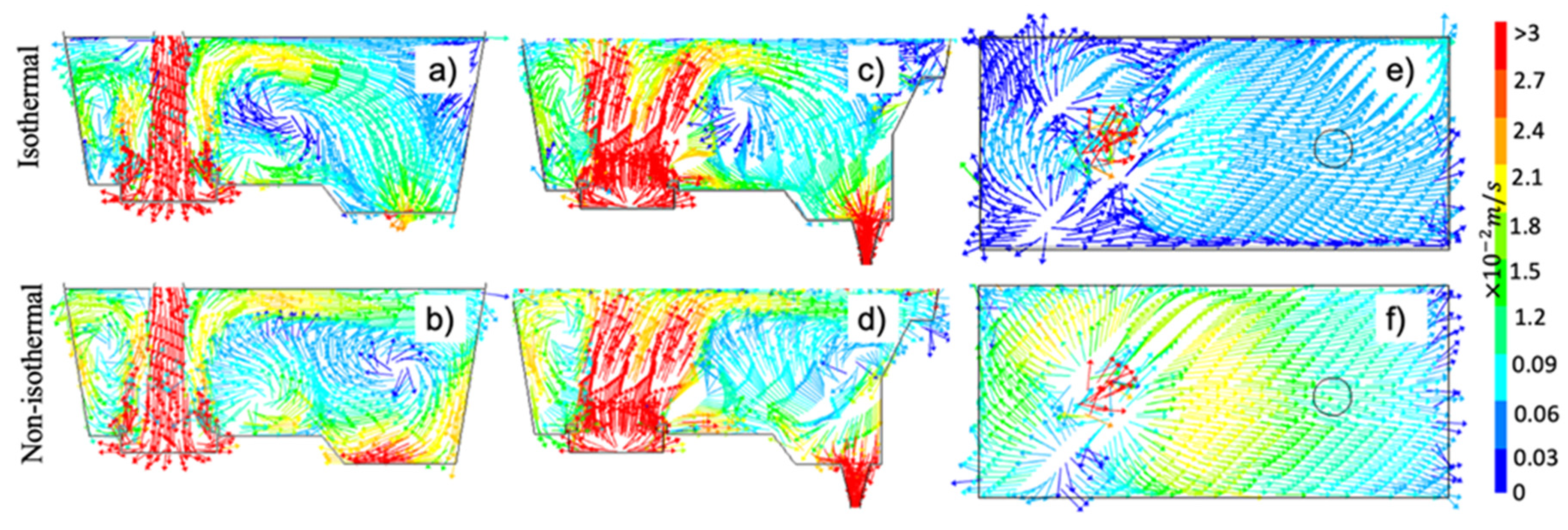
Figure 8.
Maxwell-Boltzmann distribution function for two arbitrary temperatures.

Figure 9.
Temperature contours (K) and buoyancy forces (N) at three planes [a), b)] center of the ladle shroud, [c), d)] center of the exit, and [e), f)] bath level position.
Figure 9.
Temperature contours (K) and buoyancy forces (N) at three planes [a), b)] center of the ladle shroud, [c), d)] center of the exit, and [e), f)] bath level position.

Figure 10.
Inertial forces magnitude (N) for the isothermal and non-isothermal cases.

Figure 11.
Tundish number magnitude at three planes. a) center of the ladle shroud, b) center of the exit nozzle, and c) upper view of the tundish at the bath level.
Figure 11.
Tundish number magnitude at three planes. a) center of the ladle shroud, b) center of the exit nozzle, and c) upper view of the tundish at the bath level.

Figure 12.
RTD’s for isothermal and non-isothermal cases.

Figure 13.
a) Inclusion removal percentages, b) inclusion distribution sample for both cases using 40 inclusion size.
Figure 13.
a) Inclusion removal percentages, b) inclusion distribution sample for both cases using 40 inclusion size.
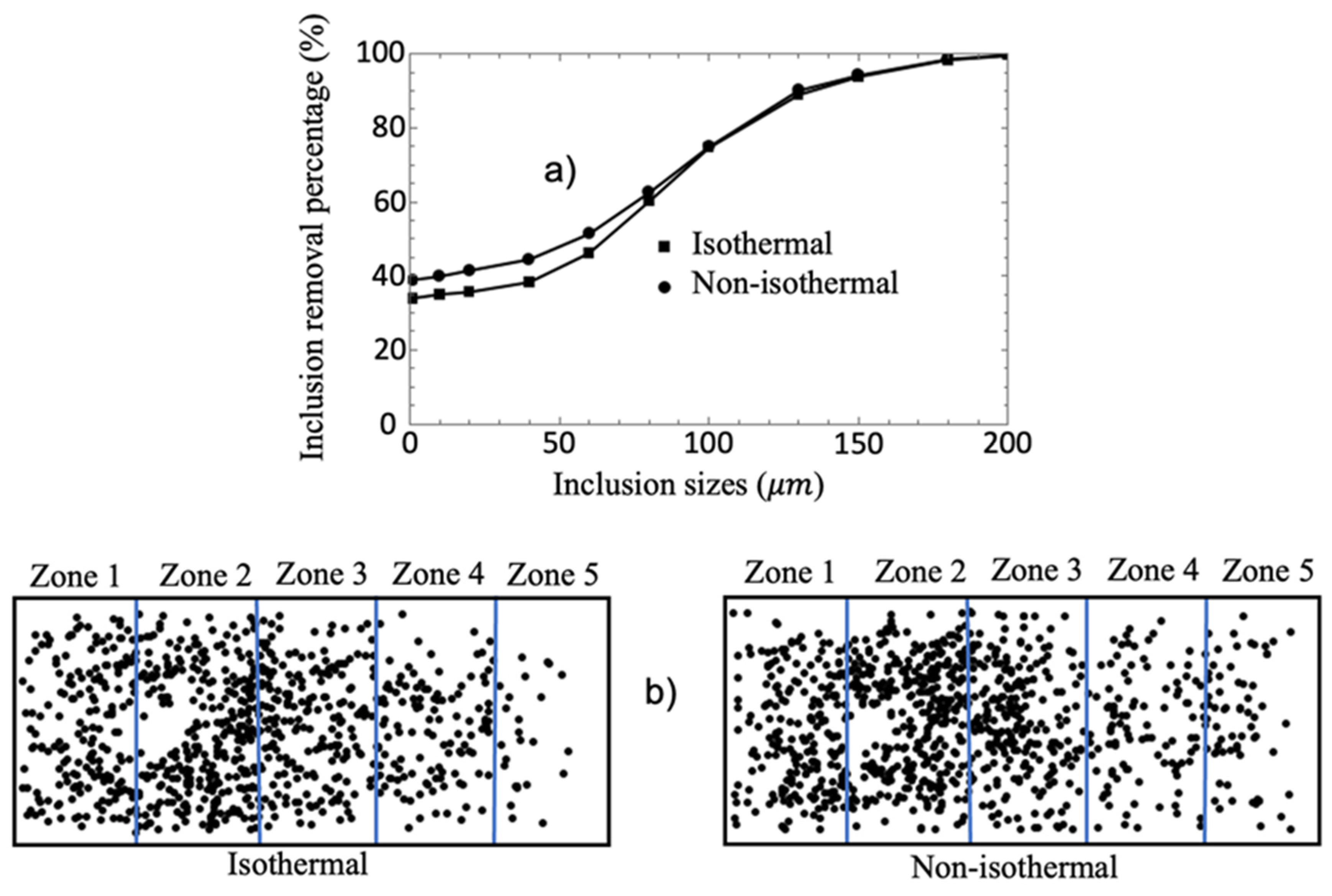
Figure 14.
Removed inclusions percentages by zones in the tundish bath level a) isothermal case, b) non-isothermal case.
Figure 14.
Removed inclusions percentages by zones in the tundish bath level a) isothermal case, b) non-isothermal case.

Table 1.
Physical properties of steel, slag, air, and magnesia.
| Property | steel | slag | air | Magnesia |
| ) | ||||
| *) | ||||
| --- |
* Thermal Conductivity.
Table 2.
Heat losses in the simulation.
| Wall | Heat loss |
| Bottom | |
| Back and front | |
| Right and left | |
| Control flow devices |
Table 3.
Volume Fractions percentages for the scaled and non-scaled models.
| Scale | ||||
| 1:3 | 46 | 40 | 14 | 0.9 |
| 1:1 | 50 | 38 | 12 | 0.92 |
Table 4.
Volume Fractions percentages for the isothermal and non-isothermal models.
| Case | ||||
| Isothermal | 50 | 38 | 12 | 0.93 |
| Non-isothermal | 46 | 39 | 15 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Deeper Flow Behavior Explanation of Temperature Effects on the Fluid Dynamic inside a Tundish
Enif Gutiérrez
et al.
,
2023
Modelling of Fluid Flow and Residence Time Distribution in a Five-strand Tundish
Dong-Yuan Sheng
et al.
,
2020
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









