Tennis environment.
In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Each agent receives its own, local observation. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
The task is episodic, and in order to solve the environment, your agents must get an average score of +0.5 (over 100 consecutive episodes, after taking the maximum over both agents). Specifically,
- After each episode, we add up the rewards that each agent received (without discounting), to get a score for each agent. This yields 2 (potentially different) scores. We then take the maximum of these 2 scores.
- This yields a single score for each episode.
The environment is considered solved, when the average (over 100 episodes) of those scores is at least +0.5.
-
Download the environment from one of the links below. You need only select the environment that matches your operating system:
- Linux: click here
- Mac OSX: click here
- Windows (32-bit): click here
- Windows (64-bit): click here
(For Windows users) Check out this link if you need help with determining if your computer is running a 32-bit version or 64-bit version of the Windows operating system.
(For AWS) If you'd like to train the agent on AWS (and have not enabled a virtual screen), then please use this link to obtain the "headless" version of the environment. You will not be able to watch the agent without enabling a virtual screen, but you will be able to train the agent. (To watch the agent, you should follow the instructions to enable a virtual screen, and then download the environment for the Linux operating system above.)
-
Place the file in the
TennisEnvironment/folder, and unzip (or decompress) the file. -
conda create --name masac python3.6 -
source activate masac -
clone the repository
git clone https://github.com/kantologist/multiagent-sac.git -
Install requirements with
pip install -r requirements.txt
You would need to run the project from the main directory using
python main.py --mode multiagent
The goal of this project was to solve the Tenis unity environment using multi agent RL. Two agents are controlling rackets to put a ball over the net. Each agent has a local observation that is continuous of 24 dimension equivalent to the position and velocity of the ball and racket. Each agent can control the movement of the racket towards the net and also jump using a 2 dimensional vector that is continuous. The reward is either +0.1 for hitting the ball over the net and -0.01 for letting the ball touch the ground or go out of bounds. The task is solved when the average score (over 100 episode) is above 0.5. The score for each episode is the maximum of the undiscounted reward of each agent.
A centralized training, centralized execution approach was used for multi agent learning. All agents shared the same Soft Actor Critic(SAC) network. Transitions of state, action, next state and reward of all agents were stored in the same replay buffer of a maximum size 10000. Transitions from the buffer were later sampled for updating the agent. SAC is able to maximize both the agent's reward and entropy thereby leading to a much more sample efficient and stable learning process.
Four different networks were used. Two Q-functions to reduce ploicy bias, one V-function which was softly updated to deal with stability and a actor network.
All Four networks were trained with adam optimizers using the same learning rate of 3e-4 and a batch size of 64. The parameters used are describe in the table below.
| Name | Data Type | Use | Value |
|---|---|---|---|
| Buffer size | int | configuration for maximum capacity of the replay buffer | 10000 |
| Learning rate | float | model learing rate | 3e-4 |
| Tau | int | Controls the soft update of target network | 5e-3 |
| Epsilon Decay | float | This determines how the epsilon decreases during training | 0.9 |
| Gamma | float | discount factor | 0.99 |
| Initial Random Steps | int | determines how many random step is taken before exploiting the model | 1e2 |
| Policy Update Frequency | int | determines the frequency of updating the policy | 2 |
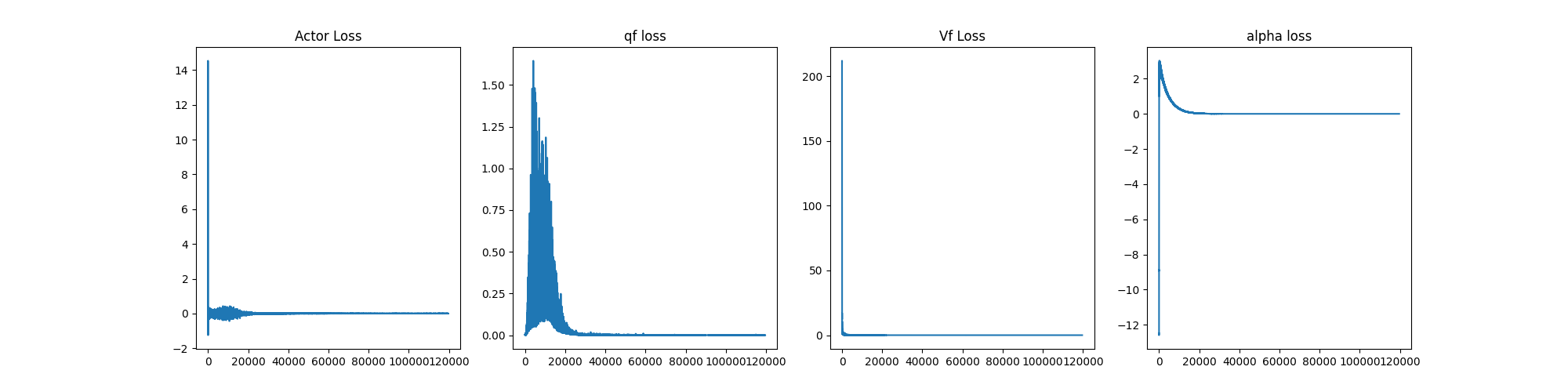
We were able to get an average score (over 100 episode) of 0.5 in about 800 episodes. The graph of the result is shown below. The graph also includes the q-function losses, the v-function loss and the actor loss. The saved weights can be found in the model_weight directory as model_weight/mqf1.pt,
model_weight/mqf2.pt, model_weight/mvf.pt and model_weight/mactor.pt
Most of the code structure for SAC followed this projects here