the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
More than one landslide per road kilometer – surveying and modeling mass movements along the Rishikesh–Joshimath (NH-7) highway, Uttarakhand, India
Ravi Kumar Guntu
Alexander Plakias
Igo Silva de Almeida
Wolfgang Schwanghart
The rapidly expanding Himalayan road network connects rural mountainous regions. However, the fragility of the landscape and poor road construction practices lead to frequent mass movements alongside roads. In this study, we investigate fully or partially road-blocking landslides along National Highway (NH-7) in Uttarakhand, India, between Rishikesh and Joshimath. Based on an inventory of >300 landslides along the ∼250 km long corridor following exceptionally high rainfall during September and October 2022, we identify the main controls on the spatial occurrence of mass-movement events. Our analysis and modeling approach conceptualizes landslides as a network-attached spatial point pattern. We evaluate different gridded rainfall products and infer the controls on landslide occurrence using Bayesian analysis of an inhomogeneous Poisson process model. Our results reveal that slope, rainfall amounts, lithology and road widening are the main controls on landslide occurrence. The individual effects of aggregated lithozones are consistent with previous assessments of landslide susceptibilities of rock types in the Himalayas. Our model spatially predicts landslide occurrences and can be adapted to other rainfall scenarios, thus having potential applications for efficiently allocating efforts for road maintenance. To this end, our results highlight the vulnerability of the Himalayan road network to landslides. Climate change and increasing exposure along this pilgrimage route will likely exacerbate landslide risk along the NH-7 in the future.
- Article
(6379 KB) - Full-text XML
-
Supplement
(223470 KB) - BibTeX
- EndNote
Roads weave across the Earth's surface, with their number and extent continually expanding. Compared to 2010, the total length of roads globally is expected to increase by 60 % by 2050 (Laurance et al., 2014), increasingly dissecting and fragmenting ecosystems. In mountainous regions, road construction leads to profound changes in the stress distribution of adjacent hillslopes, redistribution of rock and soil, and alterations of drainage patterns. If poorly implemented, road construction, inapt slope protection and insufficient drainage thus enhance slope instability and the frequency of landslides, with substantial economic damages and an increasing number of fatalities (Bíl et al., 2014; Laimer, 2017; McAdoo et al., 2018; Muenchow et al., 2012; Ozturk et al., 2022). A worldwide surge in the proposals for new roads thus warrants investigation of the link between road network expansion and landslide risk (Laurance et al., 2014).
Roads are at the heart of the Himalayan transport infrastructure. They are vital for national and international trade and passenger movement and are strategically important in border areas. India has improved and expanded its road network in mountainous states, e.g., under the national Bharatmala Pariyojana Road to Prosperity initiative established in 2015. Key objectives of this highway development program are to improve the efficiency and connectivity of the transport infrastructure and to provide road access to remote border regions and rural areas (Boora and Karakunnel, 2024). Yet in mountainous environments, roads are exposed to various degradation processes. Among these processes, mass movements in particular inflict severe structural damage and heavily degrade road serviceability (Meyer et al., 2015). Traffic disruptions due to mass movements can have severe consequences if they impede accessibility and compromise rescue operations during extreme events such as cloudbursts, floods and earthquakes (Sharma et al., 2014). Ensuring accessibility and connectivity during such events is thus of live-saving importance, yet requires considerable maintenance efforts (Uniyal, 2021).
According to the National Crime Records Bureau (2022), 160 people died due to landslides in Uttarakhand in the preceding 4 years. These figures exclude other extreme events like heavy rainfalls, floods, or the 2021 Chamoli rock and ice avalanche with over 200 fatalities (Shugar et al., 2021). Several studies have addressed mass movements and their relation to transport infrastructure in the Indian and Nepalese Himalayas. The studies range from purely phenomenological descriptions (e.g., Bartarya and Valdiya, 1989; Sarkar and Kanungo, 2006) to statistical (Das et al., 2012; Devkota et al., 2013; Sur et al., 2020) and physically based modeling approaches (e.g., Kanungo et al., 2013; Prasad and Siddique, 2020). In fact, the space limitation in steep terrain often requires road construction to undercut slopes beyond their angle of repose, reducing slope stability and increasing landslide susceptibility (e.g., Barnard et al., 2001; Haigh and Rawat, 2011; Li et al., 2020). The increase in mass wasting due to road construction itself may be similar to the impact of a large earthquake (Tanyaş et al., 2022). Therefore, particular attention has been focused on detailed stability assessments of road cut slopes (e.g., Kundu et al., 2016; Siddique et al., 2017; Siddique and Pradhan, 2018; Singh et al., 2014) and the development of appropriate remedial measures (e.g., Adhikari et al., 2020; Asthana and Khare, 2022; Koushik et al., 2016; Rawat et al., 2016), but fewer studies have attempted to predict the spatial occurrence of mass movements along roads (Huat and Jamaludin, 2005; Ching et al., 2011). Knowledge about where and when landslides preferably detach is important for early warning but also for efficiently allocating efforts of road maintenance and slope enforcement (Haigh, 1984). Using data on occurrences of landslides, susceptibility studies aim to quantify the spatial propensity of hillslopes to fail and to determine the controlling factors such as terrain attributes, e.g., slope angle and aspect, and geo-environmental variables, e.g., rainfall intensity and lithology.
In this study, we carry out an analysis of road exposure to landslides for a ∼250 km long stretch of National Highway 7 (NH-7) that connects the cities of Rishikesh and Joshimath, Uttarakhand, India (Fig. 1). We conducted a detailed survey of partially or fully road-blocking landslides along the road, following the monsoon season (May–August) and a period of intense rainfalls during 5–12 October 2022. Limiting the inventory to road-blocking landslides was required to cope with the overwhelming number of landslides, and to ensure that we account for the landslides that detached most recently. In addition, construction work for road widening often stripped away the vegetation, so differentiating between actual non-blocking landslides and excavated slopes was not straightforward. In contrast to previous studies that focused on the prediction of landslides in two spatial dimensions (e.g., Das et al., 2012; Devkota et al., 2013), our analysis and modeling approach conceptualizes landslides as a network-attached spatial point pattern (Baddeley et al., 2021).
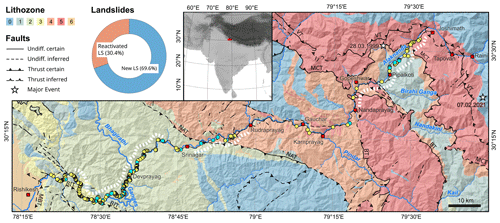
Figure 1Map of the study site. Landslides, lithozones and major faults along NH-7 from Rishikesh to Joshimath. Lithozones were defined according to their dominant lithology: (1) carbonate rocks, (2) phyllite and shale, (3) quartzite, (4) quartzite and igneous rocks, and (5) crystalline high-grade metamorphic rocks (Table 2). Note that lithozones 0 and 6 are not crossed by the road and are therefore omitted from the description. We subdivided the landslides into new ones and reactivated ones. White stippled lines indicate the road segments that have undergone widening (Sati et al., 2011). Lithozones and faults were modified from digital maps provided by the Geological Survey of India (2022). Stars indicate locations of the 1999 Mw 6.6 Chamoli earthquake (Kayal et al., 2003; USGS, 2022) and the 2021 Chamoli rock and ice avalanche (Shugar et al., 2021). MBT – Main Boundary Thrust; BIT – Bijni Thrust; NAT – North Almora Thrust; BT – Baijnat Thrust; MCT – Main Central Thrust; and VT – Vaikrita Thrust.
Landslide susceptibility analysis commonly relies on discretizing the study region into pixels, where each pixel indicates either the presence or absence of landslides. Subsequently, techniques such as logistic regression are used to predict the probability of a landslide as a function of a number of predictor variables. A pixel-based logistic regression analysis is approximately equivalent to a Poisson point process model if the landslides are originally stored as point features (Baddeley et al., 2010). We take this approach to modeling landslide susceptibility using point process models a step further by conceptualizing landslides as point features that are located on or alongside the road network (Okabe and Sugihara, 2012). This means that we do not analyze road-attached landslides as events that occur on a continuous and unbounded plane but rather as events that are alongside roads. The term alongside indicates a somewhat broad spatial relation but “implies that the physical unit of the event ... has an access point on a network” (Okabe and Sugihara, 2012, p. 7). In our case, this means that a landslide intersects with the road and blocks it. These intersections are, at the scale of our analysis, represented by point features, i.e., points on a network. Our approach relies on the analysis of the spatial arrangement of the points (the point pattern) along the line, and we hope to reveal important features (e.g., trends in point density) with respect to geo-environmental variables. An additional objective of this study is to test whether such an approach would be particularly feasible to determine the inter-relationship of linear infrastructure and landslides. One of the critical covariates in our modeling approach is the spatial distribution of accumulated rainfall amounts. We thus evaluate different rainfall products. Finally, we infer the controls on landslide occurrence using Bayesian analysis of multivariate log-linear models.
The NH-7 ascends from 400 m at Rishikesh to approximately 2000 m at Joshimath, crossing steep terrain with soil mantled slopes. Mean annual rainfall (1970–2019) varies from 1500 to 2000 mm around Rishikesh to 1000–1200 mm in Joshimath, with 80 %–86 % and 60 %–70 % delivered by the Indian summer monsoon (June to September), respectively (Pai et al., 2014; Swarnkar et al., 2021). Air temperature in Rishikesh is always above freezing and ranges between 4 and 40 °C, whereas the temperature in Joshimath varies between −10 and 20 °C. This climatic gradient is evident in the gradual transition of vegetation. In the lower-lying subtropical region, dense deciduous forests dominate. As elevation increases, these forests give way to temperate broadleaf mixed forests and temperate shrub and grassland communities.
The geological framework of the study area is largely determined by the ongoing Indo–Asian collision that causes crustal thickening and exhumation along large-scale detachment zones and thrust faults. Most of the study area lies within the Lesser Himalaya, between the Main Boundary Thrust in the south and the Main Central Thrust (MCT) in the north, which are both splays of the root detachment, the Main Himalayan Thrust (Fig. 1). As the present-day India–Eurasia convergence is on the order of 36–40 mm yr−1 (e.g., Wang et al., 2001) and approximately half of this is accommodated within the Himalayas (e.g., Lavé and Avouac, 2000), the region is seismically active and bears the potential for large earthquakes (e.g., Kayal et al., 2003; Bollinger et al., 2014; Rajendran et al., 2017).
The highway runs perpendicular to the strike of the orogen and crosses rocks of the Lesser Himalayan Sequence (LHS) and the High Himalayan Crystalline (HHC). These units represent the ancient passive Indian margin and are separated by the MCT. The LHS is mainly composed of sedimentary and low-grade metasedimentary rocks, quartzite, shale, phyllites, and slate with occasional limestone and dolomite, whereas the HHC is characterized by high-grade schist, gneiss and quartzite. These rocks feature a high density of discontinuities like faults, fractures and joints that are important seepage pathways. In locations where the road cuts through weathered rocks and intersects with major faults, the hillslopes are particularly fragile (Prasad and Siddique, 2020).
During the week preceding our survey, large parts of north India experienced a period of strong rainfall. The state of Uttarakhand registered a departure of 1040 % from the long-term (1961–2010) average. The districts of Tehri Garhwal, Pauri Garhwal, Rudraprayag and Chamoli, through which the NH-7 runs, recorded a weekly surplus of 419 %, 679 %, 218 % and 1855 %, respectively (Table S2). Given that the average rainfall amount in October is around 35 mm, approximately 3 times the monthly average rainfall occurred in only 1 week, which is close to the rate that prevails during the monsoon.
The NH-7 is a lifeline for socioeconomic development, which is mainly based on agriculture, trade, tourism, mining and hydropower. Furthermore, the highway is vital for the Indian military to transport personnel and equipment to their outposts along the Indian and Chinese–Tibetan border. Between May and October, more than 1 million pilgrims travel the highway to visit the holy shrines of Badrinath and Kedarnath. Moreover, the highway follows the course of the Ganges and its tributary Alaknanda and thus passes the river confluences known as the five Prayags, namely Devprayag, Rudraprayag, Karnaprayag, Nandaprayag and Vishnuprayag (Fig. 1). In Hinduism, these confluences are considered sacred, attracting pilgrims who bathe in the waters before worshiping the rivers. Finally, there are 10 hydroelectric power plants within 20 km distance to the road, and more projects are planned or under construction, highlighting the road's significance for energy security and economic value.
Traveling to fieldwork in the Chamoli area (Uttarakhand) on 15 October 2022, we recognized numerous partially road-blocking landslides along the road and decided to investigate their occurrence using the following approach.
First, we started to record these landslides using handheld GPS devices, as road workers had already begun to clean the road of the debris, thus rapidly removing evidence of smaller landslides that had detached in close vicinity to the road. We registered landslides along the road on our way from Rishikesh to Joshimath (Fig. 1) on 15 and 16 October, as well as on our way back on 18 October 2022. We only recorded landslides with runouts affecting the road, thus partially or fully blocking it (Fig. 2). We classified the landslides as partially blocking if the emplaced deposits either substantially narrowed the road or debris ran over marginal road markings. Very small landslides with an area of less than ∼10 m2 were not considered. Secondly, we cross-checked each recorded landslide with Google Earth using the most recent and historic high-resolution imagery. The images enabled us to identify the landslides that occurred between January and October 2022, encompassing the entire annual monsoon season as well as the heavy rainfall period at the beginning of October 2022. We initially tried to attribute the landslides to the latter period by matching our data with the acquisition dates of the images, but the temporal resolution for many road sections was insufficient. Moreover, historic imagery has become unavailable for India (https://www.thehindu.com/news/national/google-historical-satellite-imagery-disappears-for-india/article66834033.ece, last access: 25 June 2024). We also identified reactivated landslides, where a slip surface and a scar were visible in the imagery prior to January 2022. This was not always straightforward since landslide scars cannot always be clearly distinguished from bare, engineered slopes and road widening. Landslides confidently determined to have occurred before January 2022, as well as those obscured by shadows in Google Earth images, were omitted from the analysis.

Figure 2Examples of partially road-blocking landslides along the highway NH-7. Panels (a) and (c) show locations where hillslopes parallel the foliation and/or bedding. Panels (e) and (f) show a landslide that was reactivated in the observation period (Google, © 2024 Airbus).
Thirdly, we analyzed landslides along the road as a network-attached spatial point process. A spatial point process is a stochastic mechanism that controls the spatial distribution of events or occurrences (Baddeley et al., 2015). As our mapped landslides are events that occur along the road – and only these have been mapped – these events are constrained to lie on a network of lines (Baddeley et al., 2021; Okabe et al., 2006). In our case, the network is rather simple as it consists of only one polyline, but the approach can be equally applied to more complicated network topologies.
We used the open-source MATLAB extension TopoToolbox (Schwanghart and Scherler, 2014) and its numerical object PPS (Schwanghart et al., 2021) to analyze, visualize and model the density of landslides along the road. PPS means point patterns on stream networks, but it can be used with any type of dendritic, undirected network. The numerical approach consists of a fine-pixel approximation, which is controlled by the geometry of the digital elevation model (DEM) from which the data are retrieved. This means that the vector shape of the road is pixelated with the same geometry as the DEM (Schwanghart et al., 2021). We model landslide densities with an inhomogeneous Poisson process model, which is defined by the intensity function λ(u), with u being the horizontal distance along the road. A common parametric model of the intensity is the log-linear model:
where X is a matrix of predictor variables (covariates) that vary along the road, β0 is an intercept and β is a vector of model parameters. Our approach uses a spatial logistic regression, where the relation between presence probabilities p and explanatory variables X is controlled by the form of the logistic link function logit . As pixel size tends to zero, we have p→0 and . The limiting Poisson intensity is thus a log-linear function of the covariates (Baddeley et al., 2010). A key property of the model is that the events are independent from each other; i.e., the probability of landslide occurrence is independent from landslides nearby. Spatial dependence of events can occur in different ways, leading to clustering, i.e., points tend to occur close to other points, or inhibition, i.e., there is a characteristic distance or regularity in the spacing between the points. Spatial clustering of landslide events has previously been addressed by Lombardo et al. (2018, 2019) using a Cox process model to emulate the latent spatial effects of unobserved variables, whereas inhibition can be observed, for example, in data where areal non-overlapping phenomena are represented as points (Evans, 2012; Schwanghart et al., 2021). At this stage, we will not include these potential second-order effects on the density of landslides in our model, but we will investigate their possibility using the inhomogeneous K function defined by Ang et al. (2012) once we have modeled first-order effects.
We used the following candidate predictor variables in the log-linear model introduced above. First, we hypothesized that steep hillslope gradients next to the road are more susceptible to mass wasting events. Therefore, we calculated surface gradients based on the Copernicus 30 m DEM (European Space Agency, 2021). We identified areas that lie to the right or left of the road and that are higher than the road itself within a buffer zone of ∼210 m (or 7 pixels). We then selected the nearest DEM pixels and mapped the mean slopes of these nearest pixels to the road network. We chose 210 m (7× the spatial resolution of the DEM) to have sufficient pixels to obtain robust estimates of the slope. These values still vary greatly over short distances along the road and thus we smoothed them using the algorithms (with smoothness penalty parameter K=4) described by Schwanghart and Scherler (2017).
Rainfall patterns exert a strong influence on the spatial occurrence of landslides (e.g., Ching et al., 2011; Joshi and Kumar, 2006; Gariano and Guzzetti, 2016; Ozturk et al., 2021). Thus, we chose five rainfall/precipitation products (see Table 1) to characterize spatial patterns of accumulated rainfall between 1 January and 10 October 2022. Among the five rainfall/precipitation products, IMD1 relies solely on the interpolation of gauge-based measurements from a network of stations provided by the Indian Meteorological Department (Pai et al., 2014). In addition to gauge measurements, IMD2 is enhanced with estimates from the Integrated Multi-satellite Retrievals for Global Precipitation Measurement (IMERG) (Mitra et al., 2009). MSWEP v2 is another merged product that incorporates reanalysis-based, gauge and satellite-derived rainfall estimates (Beck et al., 2017). CHIRPS v2 provides a high-resolution record by combining gauge and satellite data from the NOAA (National Oceanic and Atmospheric Administration; Funk et al., 2015), and the IMERG late run provides gridded multi-satellite precipitation estimates with quasi-Lagrangian time interpolation from NASA (National Aeronautics and Space Administration; Huffman et al., 2019). We projected the geographic coordinates of the rainfall/precipitation grids to UTM zone 44N and bilinearly resampled the data to the resolution of the DEM before extracting the values of each road pixel.
Next, we incorporated information about road widening by creating a logical mask that identifies the widened segments of the highway. Due to the absence of more-detailed data, we rely on the map by Sati et al. (2011), which shows the locations of road widening completed before the 2010 monsoon season. Our envisioned strategy of compiling a more recent database of road widening using historic imagery from Google Earth was rendered impossible after most of the historic images were removed from the public archive in April 2023.
Finally, we obtained a digitized version of the lithological map of Uttarakhand (map scale 1:2 000 000) from the Geological Survey of India (2022). The data contain both stratigraphic and lithological information. Accordingly, the NH-7 crosses 34 different lithologies between Rishikesh and Joshimath. To reduce the number of categories, we summarized and aggregated the lithological information into lithozones with a lesser focus on the stratigraphic context. This aggregation resulted in five lithozones that are dominated by carbonate rocks (1), phyllite and shale (2), quartzite (3), quartzite and igneous rocks (4), and crystalline high-grade metamorphic rocks (5). The reclassification is shown in Table 2. Again, we gridded these data and assigned corresponding lithozones to each road pixel.
Table 2Definition of lithozones.
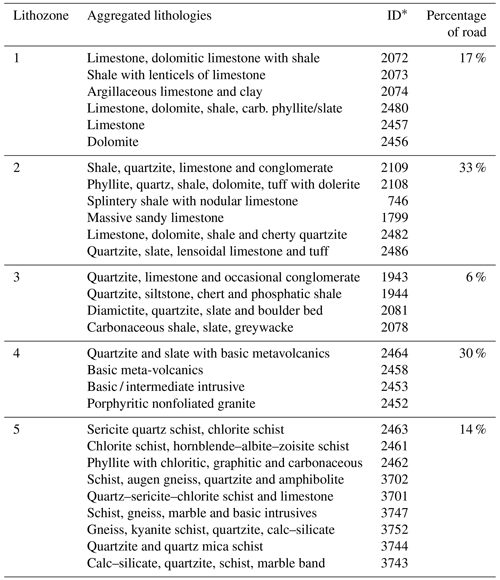
* ID refers to the UID given in the original data (Geological Survey of India, 2022).
We adopt a Bayesian strategy to infer and identify predictor variables using the function bayesloglinear of the PPS numerical class (Schwanghart et al., 2021). The function provides an interface to bayesreg (Makalic and Schmidt, 2016), a MATLAB toolbox that enables efficient Bayesian modeling and regularization of high-dimensional data. We use a Bayesian lasso estimator with Laplace prior distributions for the regression coefficients (Park and Casella, 2008). This prior results in posterior-mode estimates that are similar to estimates obtained with the lasso penalty (van Erp et al., 2019). Before calculating 1000 samples of the posterior parameter distributions, we calculated 1000 burn-in samples. These are calculated to ensure that the Gibbs sampler converges to the target distribution. In addition, we used a level of thinning of five samples. This means that only every fifth sample was retained in the generated sequence to reduce autocorrelation between the samples and to obtain more independent and representative Bayesian posterior distributions. To this end, we find that 1000 samples are sufficient to characterize the posterior distributions.
Finally, we evaluate the model based on the receiver-operating characteristics (ROC) area-under-the-curve (AUC) approach (e.g., Hanley and McNeil, 1982). We visualize the predictions and inspect and analyze spatial densities obtained from random realizations of the fitted inhomogeneous Poisson process model. Moreover, we evaluate the predictive performance of the model using a 5-fold cross-validation. In this approach, we subdivide the road into 15 km segments, which are then randomly partitioned into five groups. The first group is used as test data while the remaining groups are used to train the model. This step is then repeated for each group and the performance summarized with the AUC. In addition, we test whether additional covariates provide opportunities for further improving the model. The selected attributes include terrain roughness and total curvature as well as land cover derived from the Copernicus Global Land Operations (CGLOPS-1; moderate dynamic land cover 100 m, version 3; Buchhorn et al., 2020), which we reclassify according to Table 3. We investigate these models using a frequentist modeling approach (see the PPS function fitloglinear) and compare models with additional covariates with the Akaike information criterion (AIC, Akaike, 1974).
We recorded 309 fully or partially road-blocking landslides along the 247 km long road between Rishikesh and Joshimath, which amounts to an average landslide density of 1.25 landslides per kilometer. A two-sample Kolmogorov–Smirnoff test between the road distance (uniform distribution between start and end of the surveyed road) and the road distances measured at the landslides rejects the null hypothesis, with p≈0 that landslide locations follow a completely random spatial distribution. Visually inspecting the landslide locations using Google Earth reveals that 80 % of the recorded landslides with road blockages occurred after January 2022 (Fig. 1). Of these 250 landslides, 30 % were most likely reactivated because they could not be identified as road blocking before the rainy season (Fig. 2e and f).
The spatial distribution and amounts of accumulated rainfall between 1 January and 10 October differ between the rainfall products (Fig. 3). Since independent measurements based on rain gauges are unavailable, we investigate the performance of the rainfall products to explain the spatial distribution of landslides. The approach uses the AIC to iteratively evaluate five models that include hillslope gradient, lithozones and road widening but each using a different rainfall product. AIC values vary between 1876 and 1913, with CHIRPS v2 having the lowest AIC. CHIRPS v2 correlates positively with landslide density, whereas all other rainfall products show negative or no significant correlation (see Table 1 and Figs. S1–S5). We thus use CHIRPS v2 in the development of the subsequent models. We emphasize that including different rainfall products in the model has no strong effect on the remaining model parameters that determine the influence of slope and lithozones and road widening (see Table S1). In other words, while determining the overall performance, the choice of rainfall product does not affect our results and conclusions about the topographic and lithologic controls on landslide occurrence.
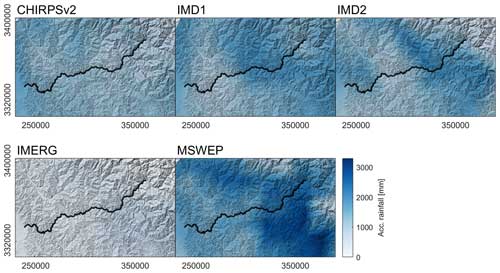
Figure 3Accumulated rainfall/precipitation amounts from different gridded products between 1 January and 10 October 2023. The sources of these data products are listed in Table 2. The black line indicates the road between Rishikesh and Joshimath (see Fig. 1).
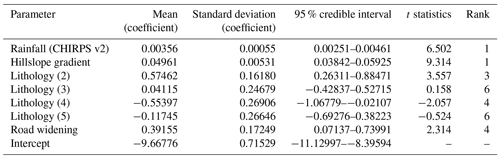
Bayesian log-linear modeling of the landslide density (Figs. 4 and 5a and b) reveals a credible influence of the covariates rainfall (Fig. 5c), slope (Fig. 5d), lithozones (Fig. 5e) and road widening (Fig. 5f; see Fig. 4 for posterior means and 95 % highest density intervals and Fig. 6 for individual effects). A Bayesian feature rank algorithm based on the absolute magnitude of the parameters in each posterior sample (Makalic and Schmidt, 2011) ranks slope as the top covariate in terms of explanatory power together with rainfall, followed by road widening and lithozones (Table 4). Among the lithozones, zones 2 and 4 stand out as categories improving the explanatory power of the model. The individual effects of the covariates reveal a positive influence of rainfall and slope on landslides (Fig. 6a and b). Predictions of landslide densities in lithozone 4 are credibly lower than in lithozone 2 (Fig. 6c). Also, our model suggests that road widening affects the density of landslides. Corrected for the influence of other parameters, average densities are twice as high in widened road sections (Fig. 6d). The spatial pattern of predicted landslide density (Fig. 5g) is consistent with observed spatial density variations, but the high small-scale variability reflects the importance of slope as a predictor variable.
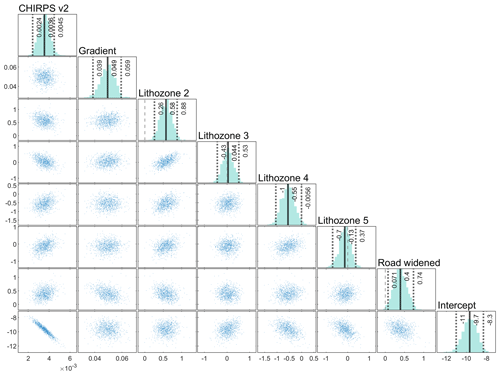
Figure 4Posterior parameter samples of the log-linear model of landslide occurrence along the NH-7. CHIRPS v2 is the gridded rainfall product, gradient determines the slope within 210 m of the road and lithozones were aggregated from a geological map. Note that lithozone 1 is missing since the parameter is encapsulated in the intercept.
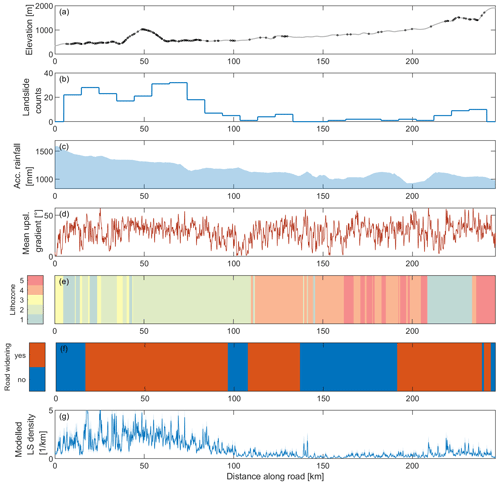
Figure 5Predictor and response variables used in the model. Panel (a) shows the occurrences of the fully and partially road-blocking landslides together with the elevation profile of the road. (b) Landslide density along the road measured using histogram binning (bin width is 9.8 km). (c) Accumulated rainfall between 1 January 1 and 10 October 2022 from CHIRPS v2. (d) Mean upslope gradient within a distance of 210 m of the road. (e) Lithozones along the road (see also Fig. 1). (f) Widened road segments. (g) Predicted landslide density using a model involving rainfall, slope, road widening and lithozones as covariates.
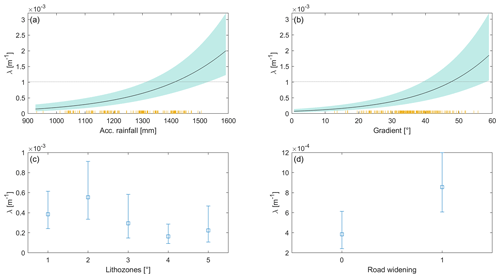
Figure 6Main effects of predictors in the log-linear model of road-blocking landslides along the NH-7. (a) Effect of accumulated rainfall amount between 1 January and 10 October 2022 on the occurrence of landslides, averaging out the effects of the other predictors. The orange lines indicate the occurrences of landslides. (b) Effect of hillslope gradient, (c) of lithozone and (d) of road widening.
Table 4Summary of posterior distributions of parameters fitted by the Bayesian log-linear point process model. Ranks in the model were calculated according to Makalic and Schmidt (2011).
The AUC is an aggregated metric for a point pattern model across thresholds and ranges between 0.5 and 1, with values close to 1 indicating high performance of the model. Our log-linear model has an AUC value of 0.79 (Fig. 7a). The inhomogeneous K function shown in Fig. 7b quantifies the expected number of points as a function of distance from each point, adjusted for the modeled inhomogeneous intensity of the point pattern. Distances between individual landslides are calculated as the shortest-path distance along the road rather than the direct Euclidean distance. Acceptance intervals around the theoretical K function were derived from repeated simulations of the inhomogeneous Bayesian log-linear model. The actual point pattern's K function is within these acceptance intervals, suggesting that the landslide locations do not exhibit clustering. A comparison of 100 randomly simulated and actual point densities (Fig. 7c) shows that the modeled and observed spatial landslide densities are consistent, although the second, smaller peak of landslide densities close to Joshimath is not captured by the model well. Moreover, 5-fold cross-validation based on 15 km long road segments reveals AUC values between 0.77 and 0.78.
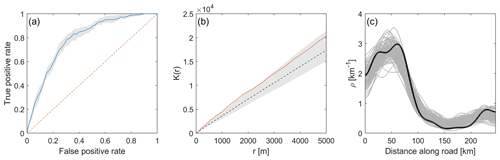
Figure 7Evaluation of the log-linear model including rainfall, slope, lithozones and road widening. (a) Receiver operating characteristics (ROC) curve. The area-under-the-curve (AUC) metric is 0.79 (0.76–0.82, 95 % bootstrap confidence intervals). (b) The inhomogeneous K function corrects for the influence of an inhomogeneous Poisson point process model and tests for second-order effects (e.g., spatial clustering). Acceptance intervals of a theoretical model with independent point independence are shown in gray and were computed from 100 bootstrap samples. The red line is the empirical inhomogeneous K function. As the curve remains within the bootstrapped acceptance intervals, we retain the null hypothesis of inter-point independence. (c) Comparison of observed landslide densities (black line) with densities obtained from 100 random realizations (gray lines) from the model.
Can the model be improved by incorporating more explanatory covariates? Our impression in the field was that landslides detach independently of planform hillslope geometry, as they occurred on spurs and in convex hollows. Nevertheless, we calculated total curvature and topographic roughness as potential predictor candidates. In addition, we used land cover (Table 3) and distance to faults (Fig. 1), as they are commonly used in susceptibility studies (e.g., Stanley and Kirschbaum, 2017; Li et al., 2020; Ozturk et al., 2021) and potentially control the density of roadside slope failures. Yet including these metrics in the model barely contributes to improving the model fit, and their incorporation in the model would, according to the constancy of the AIC, lead to overfitting (Fig. 8).
We recorded more than one landslide per road kilometer along the NH-7 between Rishikesh and Joshimath. The fact that this road is strongly affected by landslides has been previously described and attributed to the region's fragile slopes, intense rainfall and frequent seismicity (Sati et al., 2011). In addition to the environmental conditions, road construction and widening have contributed to the occurrence of new landslides, which are often shallow and small, but nevertheless lead to fatalities, inflict severe damage on infrastructure and cause traffic disruption (Sati et al., 2011). We conducted a systematic survey of roadside landslides and derived a statistical model that quantifies landslide susceptibility along the NH-7 at a high spatial resolution.
Our analysis relied on a GPS-based survey of landslides while traveling from Rishikesh to Joshimath shortly after a period of anomalously high rainfall. Using this approach, we mapped landslides irrespective of cloud cover and without acquiring high-resolution satellite imagery, which is usually needed to reliably detect small landslides. A drawback, however, is that we may have missed landslides where debris had already been removed by road work. Also, detailed mapping of the areal extent of the landslides was not possible during drive-by, so we did not quantify the size of landslides. Thus, our analysis treats all landslides the same, irrespective of their areal extent and volume. To this end, however, this enables us to adopt a modeling approach that conceptualizes landslides as an unmarked network-attached point pattern (Baddeley et al., 2021; Okabe and Sugihara, 2012). Representing landslides as network-attached points and not as areal features has advantages and disadvantages. Constraining landslide locations to lie on roads demands that all predictor variables also need to be mapped to the road network, which entails some generalization and additional degrees of freedom about the choice and aggregation of 2D variables. For landslide susceptibility analysis, for example, this means that spatial variables characterizing the source area (e.g., hillslope gradient) are projected onto the road. At the same time, model development and fitting benefits from smaller sample sizes so that data amounts are moderate and computational demands during Bayesian posterior sampling remain manageable.
We detected a profound difference between rainfall products, a detailed analysis of which is outside the scope of this study. Several studies along the Himalayan orographic front have previously detected these differences. They have been attributed to the sparse network of rain gauges or, in cases where rainfall estimates are based on remote sensing data, to irregular acquisition times, which can result in missing individual rainfall events (Andermann et al., 2011; Hu et al., 2016). To this end, these uncertainties are detrimental to accurately capturing the spatial patterns of landslides (Ozturk et al., 2021). We found that CHIRPS v2 performed best in predicting the spatial landslide patterns along NH-7, but the search strategy employed must be viewed critically as the reverse conclusion, that landslides are controlled by these patterns, is not necessarily true. Indeed, studies come to different conclusions about the performance of CHIRPS v2 and other gridded rainfall products. For example, Kumar et al. (2021) studied different gridded rainfall products in the eastern Himalayas and found that CHIRPS v2 overestimated the monsoon but underestimated annual precipitation. Based on the analysis of 18 extreme precipitation events during 2014–2016 in the northwest Himalayas (including our study site), however, Jena et al. (2020) concluded that CHIRPS v2 provides the most reliable precipitation estimates. Indeed, the two-peaked rainfall pattern of CHIRPS v2 is most consistent with long-term rainfall patterns obtained from the interpolation of 44 rainfall gauge records averaged over the period from 1901 to 1950, which show highest values along the Himalayan front and along the physiographic transition to the Higher Himalaya (Basistha et al., 2008; Bookhagen, 2010).
Lithozones derived from a geological map contributed to the explanatory power of the model, thus highlighting the role of rock properties in modulating landslide susceptibility. As we did not measure the actual geotechnical and geomechanical properties or, e.g., bedding and foliation along our route, we can only provide a first-order reasoning of the prediction capacity of the lithozones. The high landslide density in lithozone 2 is likely related to the pronounced fissility and cleavage of the dominating shales and phyllites. Moreover, material softening, percolation and weathering cause a general decrease in rock strength. Tectonic activity adds to a general decrease in rock strength by creating shear surfaces with low friction angles (Stead, 2016). In addition, road segments where the adjoining hillslopes parallel bedding, joints or foliation planes are particularly vulnerable (e.g., Bartarya and Valdiya, 1989). Conversely, lithozone 4 is characterized by quartzite and igneous rocks. These have undergone low- to high-grade metamorphism and are generally harder and have a more irregular fabric that restrains the formation of planar slide surfaces. Moreover, these rocks tend to develop more-stable regolith mantles (Gerrard, 1994) and are thus less susceptible to landsliding. Our model shows that under the same topographic conditions and rainfall amounts, the rock types of lithozone 2 are 2–6 times more susceptible to landslides than those in lithozone 4 (Fig. 6c). The remaining lithozones are not credibly different from each other. In part, the lack of differences can be attributed to the low number of samples, as only a small fraction of the road traverses these lithozones (Table 2). Notwithstanding, a general trend towards lower landslide susceptibility from lithozones 1 to 5 is consistent with a previous review study about lithological controls on the occurrence of mass movements in the Himalayas (Gerrard, 1994).
Previous studies indicate that human activities have played a crucial role in predisposing slopes to failure (Li et al., 2020; van Westen et al., 2008; Tanyaş et al., 2022). Our analysis underscores these findings and quantifies the occurrence of landslides as being twice as high along widened sections of NH-7 if other predictor variables are held constant. The process of cutting into mountain sides to create wider pathways often creates unstable slopes that are prone to failure (Barnard et al., 2001; Haigh and Rawat, 2011; Sati et al., 2011; Li et al., 2020). Clearing trees and vegetation for road widening eliminates their stabilizing influence on slopes, thereby increasing landslide hazard (e.g., Guthrie, 2002). Additionally, widened roads can lead to increased surface runoff during heavy rainfall or snowmelt, saturating the soil and making it more susceptible to landslides (e.g., Wadhawan et al., 2020). The rock blasting required during the road widening process can lead to the fracturing and weakening of rock masses, creating potential landslide-prone zones along the road corridors (Sati et al., 2011). Moreover, road widening alters natural drainage patterns and potentially redirects water flow to adjacent slopes, thus causing water saturation, erosion and instability. In fact, these disturbances have previously led to frequent landslides along the NH-7: Sati et al. (2011) also report about ∼300 landslides occurring along the road more than 10 years ago. Our data indicate that 30 % of the recorded landslides are reactivated slope failures, which highlights the fact that slopes are recurrently unstable during periods of intense rainfall (Joshi and Kumar, 2006). During mapping, we also noticed that some slopes were engineered during the last years with retaining walls, yet many of these also failed.
Clearly, our model may miss important predictor variables that control the occurrence of landslides. We included variables that characterize environmental conditions and found that slope, rainfall, road widening and lithology largely explain the variability in landslide density. Variables such as land use or topographic derivatives do not improve the performance of the model as measured by the AIC, at least at the spatial scale at which these variables were available. However, small-scale topographic changes due to construction or land use changes (e.g., abandonment and degradation of agricultural fields and terrace systems) may exacerbate roadside slope failures (Jaquet et al., 2015; Mauri et al., 2022). A more-up-to-date DEM with higher resolution may indeed help to improve the spatial prediction of landslide, although higher digital terrain model resolutions were shown to not necessarily improve model performance, in particular along roads (Penna et al., 2014). Moreover, the propensity for landslides along widened segments of the road may change over time. Road widening and slope undercutting can be viewed as a perturbation to which slopes will adjust. Timescales of this adjustment may vary and depend on several factors. Likewise, remedial measures such as slope enforcement, artificial drainage and retention walls will affect slope stability. Including these activities of landslide mitigation was not possible in our study but could support planning of structural measures.
Our model hindcasts the spatial pattern of road-blocking landslides, and we posit that it can be used as a time-predictive model as well. Rainfall is one of the main covariates in the model and is also the one with the largest uncertainties, as shown by the discrepancies between the gridded rainfall products. A denser network of rain gauges and better availability of these data would likely contribute, together with weather forecasting, to more accurate estimates of landslide occurrences, which ultimately would facilitate more efficient allocation of resources for road maintenance. Also, recurrent slope failures should be monitored more closely to direct efforts for slope reinforcement. The land cover data, which we included in the model, is too coarse to capture the widespread lack of vegetation along the road. As many of the landslides were shallow, revegetating slopes may contribute to their stabilization (Vergani et al., 2017).
The NH-7 is a key arterial road, and landslides make transport of goods and people difficult, thus causing serious economic disruption. Moreover, slope failures along the road have led to fatalities in places where roads were widened, and recent heavy rainfall in July 2023 has caused several severe landslides (https://www.hindustantimes.com/india-news/ landslide-on-char-dham-road-leaves-pilgrims-stranded-heavy-rains-cause-damage-and-blockages-in-uttarakhand-101690225215947.html, last access: 26 June 2024). Such damage and commensurate fatalities may become even more frequent in the future. The entire upper Ganga Basin is susceptible to extreme rainfall events (Joshi and Kumar, 2006), and climate change projections – although subject to high uncertainties – indicate a trend towards more-frequent extreme events due to elevation-dependent warming and a likely increase in summer monsoon precipitation by 4 %–25 % (Krishnan et al., 2019). In addition, exposure to landslides is likely to increase in Uttarakhand as the Char Dham National Highway project is implemented (Chouhan et al., 2023). Road construction and increased traffic volumes attract more people, who will strive for new economic opportunities associated with sites along roads (Fort et al., 2010; Chouhan et al., 2023). These sites are often more susceptible to landslides as construction often implies vegetation removal and slope destabilization (Petley et al., 2007; Li et al., 2020). A reduction in traffic may disrupt the cycle of increasing hazard and exposure. The commissioning of the currently constructed 125 km long broad-gauge railway between Rishikesh and Karnprayag (Azad et al., 2022) might be a major step towards this goal.
Road construction is soaring in the Himalayas. During the last 5 years, ∼11 000 km of roads were built in the Indian Himalayan states (The Tribune, 2022). Yet the fragility of the Himalayan landscape as well as slope undercutting and poor construction practices make maintenance of these roads challenging. Our study of landslides along the NH-7 demonstrates the scale of this challenge as we detect more than one partially or fully road-blocking landslide per road kilometer between Rishikesh and Joshimath. We contribute to a better understanding and prediction of these landslides by creating a landslide inventory of roadside landslides and the adoption of a novel approach to landslide exposure analysis, which treats the landslides as unmarked network-attached spatial point phenomena. Together with inhomogeneous Poisson process models, this inventory enables us to identify the main controlling variables, i.e., slope angle, rainfall amount, road widening and lithology. Our model shows that if corrected for all other influences, road widening leads to a doubling of road-blocking landslides. This finding quantitatively underpins previous claims that improper construction practices of road widening increase rather than decrease landslide hazards along roads (Sati et al., 2011). The Himalayas' fragile geology and exposure to torrential rains demand proper geological assessments and mitigation measures, such as constructing retaining walls, installing drainage systems and stabilizing slopes, to minimize the impact of road widening on landslide occurrence. Thorough environmental impact assessments before road widening projects and consideration of alternative routes or transportation solutions can help strike a balance between development and preserving the delicate mountain ecosystem while reducing landslide risks.
The code and the data to run the analysis are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-24-3207-2024-supplement.
All authors conceptualized the study and conducted mapping landslides. RKG retrieved and analyzed the rainfall data. JM and AP compiled, analyzed and visualized the data, and WS conducted the statistical analysis. All authors wrote the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This article is part of the special issue “Estimating and predicting natural hazards and vulnerabilities in the Himalayan region”. It is not associated with a conference.
We acknowledge the German Exchange Service (DAAD) and the Indian University Grants Commission (UGC) for supporting Co-PREPARE, a joint project of IIT Roorkee and the University of Potsdam. Jürgen Mey acknowledges support from the research focus “Earth and Environmental Systems” of the University of Potsdam.
This research has been supported by the Deutscher Akademischer Austauschdienst (grant no. 57553291) and the Prime Minister's Research Fellowship, government of India (grant no. PM-31-22-695-414), awarded to Ravi Kumar Guntu.
This paper was edited by Olivier Dewitte and reviewed by two anonymous referees.
Adhikari, D., Tiwary, R., Singh, P. P., Suchiang, B. R., Nonghuloo, I. M., and Barik, S. K.: Trees, Shrubs and Herbs for Slope Stabilization in Landslide Prone Areas of Eastern Himalaya BT, in: Nature-based Solutions for Resilient Ecosystems and Societies, edited by: Dhyani, S., Gupta, A. K., and Karki, M., Springer Singapore, Singapore, 307–326, https://doi.org/10.1007/978-981-15-4712-6_18, 2020.
Akaike, H.: A new look at the statistical model identification, IEEE T. Automat. Contr., 19, 716–723, 1974.
Andermann, C., Bonnet, S., and Gloaguen, R.: Evaluation of precipitation data sets along the Himalayan front, Geochem. Geophy. Geosy., 12, Q07023, https://doi.org/10.1029/2011GC003513, 2011.
Ang, Q., Baddeley, A., and Nair, G.: Geometrically Corrected Second Order Analysis of Events on a Linear Network, with Applications to Ecology and Criminology, Scand. J. Stat., 39, 591–617, https://doi.org/10.1111/j.1467-9469.2011.00752.x, 2012.
Asthana, B. N. and Khare, D.: Hill Slope Stabilization at Dam and Power Projects in Himalayas BT, in: Recent Advances in Dam Engineering, edited by: Asthana, B. N. and Khare, D., Springer International Publishing, Cham, 239–264, https://doi.org/10.1007/978-3-030-32278-6_11, 2022.
Azad, M. A., Singh, S. K., Alok, A., Meenakshi, Shekhar, S., and Kumar, P.: Geotechnical and geological studies of Adit-6 of the railway tunnel between Rishikesh and Karnprayag in India focusing on the excavation methods and design of support analysis: a case study, Arab. J. Geosci., 15, 129, https://doi.org/10.1007/s12517-021-09355-7, 2022.
Baddeley, A., Berman, M., Fisher, N. I., Hardegen, A., Milne, R. K., Schuhmacher, D., Shah, R., and Turner, R.: Spatial logistic regression and change-of-support in Poisson point processes, Electron. J. Stat., 4, 1151–1201, https://doi.org/10.1214/10-EJS581, 2010.
Baddeley, A., Rubak, E., and Turner, R.: Spatial point patterns: methodology and applications with R, CRC press, ISBN 9781482210217, 2015.
Baddeley, A., Nair, G., Rakshit, S., McSwiggan, G., and Davies, T. M.: Analysing point patterns on networks – A review, Spat. Stat., 42, 100435, https://doi.org/10.1016/J.SPASTA.2020.100435, 2021.
Barnard, P. L., Owen, L. A., Sharma, M. C., and Finkel, R. C.: Natural and human-induced landsliding in the Garhwal Himalaya of northern India, Geomorphology, 40, 21–35, https://doi.org/10.1016/S0169-555X(01)00035-6, 2001.
Bartarya, S. K. and Valdiya, K. S.: Landslides and Erosion in the Catchment of the Gaula River, Kumaun Lesser Himalaya, India, Mt. Res. Dev., 9, 405, https://doi.org/10.2307/3673588, 1989.
Basistha, A., Arya, D. S., and Goel, N. K.: Spatial Distribution of Rainfall in Indian Himalayas – A Case Study of Uttarakhand Region, Water Resour. Manag., 22, 1325–1346, https://doi.org/10.1007/s11269-007-9228-2, 2008.
Beck, H. E., Vergopolan, N., Pan, M., Levizzani, V., van Dijk, A. I. J. M., Weedon, G. P., Brocca, L., Pappenberger, F., Huffman, G. J., and Wood, E. F.: Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling, Hydrol. Earth Syst. Sci., 21, 6201–6217, https://doi.org/10.5194/hess-21-6201-2017, 2017.
Bíl, M., Kubeček, J., and Andrášik, R.: An epidemiological approach to determining the risk of road damage due to landslides, Nat. Hazards, 73, 1323–1335, https://doi.org/10.1007/s11069-014-1141-4, 2014.
Bollinger, L., Sapkota, S. N., Tapponnier, P., Klinger, Y., Rizza, M., Van der Woerd, J., Tiwari, D. R., Pandey, R., Bitri, A., and Bes de Berc, S.: Estimating the return times of great Himalayan earthquakes in eastern Nepal: Evidence from the Patu and Bardibas strands of the Main Frontal Thrust, J. Geophys. Res.-Sol. Ea., 119, 7123–7163, https://doi.org/10.1002/2014JB010970, 2014.
Bookhagen, B.: Appearance of extreme monsoonal rainfall events and their impact on erosion in the Himalaya, Geomatics, Nat. Hazards Risk, 1, 37–50, https://doi.org/10.1080/19475701003625737, 2010.
Boora, S. and Karakunnel, M. T.: The SDG conundrum in India: navigating economic development and environmental preservation, Int. J. Environ. Stud., 81, 961–976, https://doi.org/10.1080/00207233.2024.2323321, 2024.
Buchhorn, M., Smets, B., Bertels, L., Roo, B. De, Lesiv, M., Tsendbazar, N.-E., Li, L., and Tarko, A.: Copernicus Global Land Service: Land Cover 100 m: version 3 Globe 2015–2019, Product User Manual, https://doi.org/10.5281/zenodo.3938963, 2020.
Ching, J., Liao, H. J., and Lee, J. Y.: Predicting rainfall-induced landslide potential along a mountain road in Taiwan, Geotechnique, 61, 153–166, 2011.
Chouhan, S., Thieken, A. H., Bubeck, P., and Mukherjee, M.: Role of tourism on disaster recovery: A case study of Uttarakhand, India, Int. J. Disast. Risk Re., 95, 103878, https://doi.org/10.1016/j.ijdrr.2023.103878, 2023.
Das, I., Stein, A., Kerle, N., and Dadhwal, V. K.: Landslide susceptibility mapping along road corridors in the Indian Himalayas using Bayesian logistic regression models, Geomorphology, 179, 116–125, https://doi.org/10.1016/j.geomorph.2012.08.004, 2012.
Devkota, K. C., Regmi, A. D., Pourghasemi, H. R., Yoshida, K., Pradhan, B., Ryu, I. C., Dhital, M. R., and Althuwaynee, O. F.: Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya, Nat. Hazards, 65, 135–165, https://doi.org/10.1007/s11069-012-0347-6, 2013.
European Space Agency: Copernicus Global Digital Elevation Model, Distributed by OpenTopography, https://doi.org/10.5069/G9028PQB, 2021.
Evans, I. S.: Geomorphometry and landform mapping: What is a landform?, Geomorphology, 137, 94–106, https://doi.org/10.1016/j.geomorph.2010.09.029, 2012.
Fort, M., Cossart, E., and Arnaud-Fassetta, G.: Hillslope-channel coupling in the Nepal Himalayas and threat to man-made structures: The middle Kali Gandaki valley, Geomorphology, 124, 178–199, https://doi.org/10.1016/j.geomorph.2010.09.010, 2010.
Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., Husak, G., Rowland, J., Harrison, L., Hoell, A., and Michaelsen, J.: The climate hazards infrared precipitation with stations – a new environmental record for monitoring extremes, Sci. Data, 2, 150066, https://doi.org/10.1038/sdata.2015.66, 2015.
Gariano, S. L. and Guzzetti, F.: Landslides in a changing climate, Earth-Sci. Rev., 162, 227–252, https://doi.org/10.1016/j.earscirev.2016.08.011, 2016.
Geological Survey of India: Uttarakhand lithology, Government of India, Kolkata, India, https://bhukosh.gsi.gov.in, last access: 10 August 2022.
Gerrard, J.: The landslide hazard in the Himalayas: geological control and human action, edited by: Morisawa, M., Elsevier, Amsterdam, 221–230, https://doi.org/10.1016/B978-0-444-82012-9.50019-0, 1994.
Guthrie, R. H.: The effects of logging on frequency and distribution of landslides in three watersheds on Vancouver Island, British Columbia, Geomorphology, 43, 273–292, 2002.
Haigh, M. and Rawat, J. S.: Landslide causes: Human impacts on a Himalayan landslide swarm, Belg. J. Geogr., 3–4, 201–220, https://doi.org/10.4000/belgeo.6311, 2011.
Haigh, M. J.: Landslide prediction and highway maintenance in the Lesser Himalaya, India, Z. Geomorphol. Supp., 51, 17–38, 1984.
Hanley, J. A. and McNeil, B. J.: The meaning and use of the area under a receiver operating characteristic (ROC) curve, Radiology, 143, 29–36, 1982.
Hu, Z., Hu, Q., Zhang, C., Chen, X., and Li, Q.: Evaluation of reanalysis, spatially interpolated and satellite remotely sensed precipitation data sets in central Asia, J. Geophys. Res.-Atmos., 121, 5648–5663, https://doi.org/10.1002/2016JD024781, 2016.
Huat, B. B. and Jamaludin, S.: Evaluation of slope assessment system in predicting landslides along roads underlain by granitic formation, American Journal of Environmental Sciences, 1, 90–96, 2005.
Huffman, G. J., Stocker, E. F., Bolvin, D. T., Nelkin, E. J., and Tan, J.: GPM IMERG Late Precipitation L3 1 day 0.1 degree × 0.1 degree V06, edited by: Savtchenko, A., Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/GPM/IMERGDL/DAY/06, 2019.
Jaquet, S., Schwilch, G., Hartung-Hofmann, F., Adhikari, A., Sudmeier-Rieux, K., Shrestha, G., Liniger, H. P., and Kohler, T.: Does outmigration lead to land degradation? Labour shortage and land management in a western Nepal watershed, Appl. Geogr., 62, 157–170, https://doi.org/10.1016/j.apgeog.2015.04.013, 2015.
Jena, P., Garg, S., and Azad, S.: Performance Analysis of IMD High-Resolution Gridded Rainfall (0.25°×0.25°) and Satellite Estimates for Detecting Cloudburst Events over the Northwest Himalayas, J. Hydrometeorol., 21, 1549–1569, https://doi.org/10.1175/JHM-D-19-0287.1, 2020.
Joshi, V. and Kumar, K.: Extreme rainfall events and associated natural hazards in Alaknanda valley, Indian Himalayan region, J. Mt. Sci., 3, 228–236, https://doi.org/10.1007/s11629-006-0228-0, 2006.
Kanungo, D. P., Pain, A., and Sharma, S.: Finite element modeling approach to assess the stability of debris and rock slopes: a case study from the Indian Himalayas, Nat. Hazards, 69, 1–24, https://doi.org/10.1007/s11069-013-0680-4, 2013.
Kayal, J. R., Ram, S., Singh, O. P., Chakraborty, P. K., and Karunakar, G.: Aftershocks of the March 1999 Chamoli Earthquake and Seismotectonic Structure of the Garhwal Himalaya, B. Seismol. Soc. Am., 93, 109–117, 2003.
Koushik, P., Shantanu, S., Manojit, S., and Mahesh, S.: Stability analysis and design of slope reinforcement techniques for a Himalayan landslide BT, in: Proceedings of the Conference on Recent Advances in Rock Engineering (RARE 2016), Bengaluru, India, 16–18 November 2016, 97–104, https://doi.org/10.2991/rare-16.2016.16, 2016.
Krishnan, R., Shrestha, A. B., Ren, G., Rajbhandari, R., Saeed, S., Sanjay, J., Syed, M. A., Vellore, R., Xu, Y., You, Q., and Ren, Y.: Unravelling Climate Change in the Hindu Kush Himalaya: Rapid Warming in the Mountains and Increasing Extremes, in: The Hindu Kush Himalaya Assessment: Mountains, Climate Change, Sustainability and People, edited by: Wester, P., Mishra, A., Mukherji, A., and Shrestha, A. B., Springer International Publishing, Cham, 57–97, https://doi.org/10.1007/978-3-319-92288-1_3, 2019.
Kumar, M., Hodnebrog, Ø., Sophie Daloz, A., Sen, S., Badiger, S., and Krishnaswamy, J.: Measuring precipitation in Eastern Himalaya: Ground validation of eleven satellite, model and gauge interpolated gridded products, J. Hydrol., 599, 126252, https://doi.org/10.1016/j.jhydrol.2021.126252, 2021.
Kundu, J., Sarkar, K., and Singh, A. K.: Integrating structural and numerical solutions for road cut slope stability analysis-a case study, India, in: ISRM 2nd International Conference on Rock Dynamics, Suzhou, China, 18–19 May 2016, ISRM-ROCDYN-2016-64, 2016.
Laimer, H. J.: Anthropogenically induced landslides – A challenge for railway infrastructure in mountainous regions, Eng. Geol., 222, 92–101, https://doi.org/10.1016/j.enggeo.2017.03.015, 2017.
Laurance, W. F., Clements, G. R., Sloan, S., O’Connell, C. S., Mueller, N. D., Goosem, M., Venter, O., Edwards, D. P., Phalan, B., Balmford, A., Van Der Ree, R., and Arrea, I. B.: A global strategy for road building, Nature, 513, 229–232, 2014.
Lavé, J. and Avouac, J. P.: Active folding of fluvial terraces across the Siwaliks Hills, Himalayas of central Nepal, J. Geophys. Res., 105, 5735–5770, https://doi.org/10.1029/1999JB900292, 2000.
Li, Y., Wang, X., and Mao, H.: Influence of human activity on landslide susceptibility development in the Three Gorges area, Nat. Hazards, 104, 2115–2151, https://doi.org/10.1007/s11069-020-04264-6, 2020.
Lombardo, L., Opitz, T., and Huser, R.: Point process-based modeling of multiple debris flow landslides using INLA: an application to the 2009 Messina disaster, Stoch. Env. Res. Risk A., 32, 2179–2198, https://doi.org/10.1007/s00477-018-1518-0, 2018.
Lombardo, L., Bakka, H., Tanyas, H., van Westen, C., Mai, P. M., and Huser, R.: Geostatistical Modeling to Capture Seismic-Shaking Patterns From Earthquake-Induced Landslides, J. Geophys. Res.-Earth, 124, 1958–1980, https://doi.org/10.1029/2019JF005056, 2019.
Makalic, E. and Schmidt, D. F.: A Simple Bayesian Algorithm for Feature Ranking in High Dimensional Regression Problems, in: Advances in Artificial Intelligence. AI 2011. Lecture Notes in Computer Science, edited by: Wang, D. and Reynolds, M., vol. 7106, Springer, Berlin, Heidelberg, https://doi.org/10.1007/978-3-642-25832-9_23, 2011.
Makalic, E. and Schmidt, D. F.: High-Dimensional Bayesian Regularised Regression with the BayesReg Package, arXiv [preprint], https://doi.org/10.48550/arXiv.1611.06649, 2016.
Mauri, L., Straffelini, E., and Tarolli, P.: Multi-temporal modeling of road-induced overland flow alterations in a terraced landscape characterized by shallow landslides, Int. Soil Water Conserv. Res., 10, 240–253, https://doi.org/10.1016/j.iswcr.2021.07.004, 2022.
McAdoo, B. G., Quak, M., Gnyawali, K. R., Adhikari, B. R., Devkota, S., Rajbhandari, P. L., and Sudmeier-Rieux, K.: Roads and landslides in Nepal: how development affects environmental risk, Nat. Hazards Earth Syst. Sci., 18, 3203–3210, https://doi.org/10.5194/nhess-18-3203-2018, 2018.
Meyer, N. K., Schwanghart, W., Korup, O., and Nadim, F.: Roads at risk: traffic detours from debris flows in southern Norway, Nat. Hazards Earth Syst. Sci., 15, 985–995, https://doi.org/10.5194/nhess-15-985-2015, 2015.
Mitra, A. K., Bohra, A. K., Rajeevan, M. N., and Krishnamurti, T. N.: Daily Indian Precipitation Analysis Formed from a Merge of Rain-Gauge Data with the TRMM TMPA Satellite-Derived Rainfall Estimates, J. Meteorol. Soc. Jpn. Ser. II, 87A, 265–279, https://doi.org/10.2151/jmsj.87A.265, 2009.
Muenchow, J., Brenning, A., and Richter, M.: Geomorphic process rates of landslides along a humidity gradient in the tropical Andes, Geomorphology, 139, 271–284, 2012.
National Crime Records Bureau: Accidental Deaths & Suicides in India 2021, https://www.data.gov.in/catalog/accidental-deaths-suicides-india-adsi-2021 (last access: 1 December 2022), 2022.
Okabe, A. and Sugihara, K.: Spatial analysis along networks: statistical and computational methods, John Wiley & Sons, ISBN 9781119967767, 2012.
Okabe, A., Okunuki, K., and Shiode, S.: SANET: A Toolbox for Spatial Analysis on a Network, Geogr. Anal., 38, 57–66, https://doi.org/10.1111/j.0016-7363.2005.00674.x, 2006.
Ozturk, U., Saito, H., Matsushi, Y., Crisologo, I., and Schwanghart, W.: Can global rainfall estimates (satellite and reanalysis) aid landslide hindcasting?, Landslides, 18, 3119–3133, https://doi.org/10.1007/s10346-021-01689-3, 2021.
Ozturk, U., Bozzolan, E., Holcombe, E. A., Shukla, R., Pianosi, F., and Wagener, T.: How climate change and unplanned urban sprawl bring more landslides, Nature, 608, 262–265, https://doi.org/10.1038/d41586-022-02141-9, 2022.
Pai, D. S., Sridhar, L., Rajeevan, M., Sreejith, O. P., Satbhai, N. S., and Mukhopadhyay, B.: Development of a new high spatial resolution (0.25°×0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region, MAUSAM, 1, 1–18, https://doi.org/10.54302/mausam.v65i1.851, 2014.
Park, T. and Casella, G.: The Bayesian lasso, J. Am. Stat. Assoc., 103, 681–686, 2008.
Penna, D., Borga, M., Aronica, G. T., Brigandì, G., and Tarolli, P.: The influence of grid resolution on the prediction of natural and road-related shallow landslides, Hydrol. Earth Syst. Sci., 18, 2127–2139, https://doi.org/10.5194/hess-18-2127-2014, 2014.
Petley, D. N., Hearn, G. J., Hart, A., Rosser, N. J., Dunning, S. A., Oven, K., and Mitchell, W. A.: Trends in landslide occurrence in Nepal, Nat. Hazards, 43, 23–44, https://doi.org/10.1007/s11069-006-9100-3, 2007.
Prasad, S. and Siddique, T.: Stability assessment of landslide-prone road cut rock slopes in Himalayan terrain: A finite element method based approach, J. Rock Mech. Geotech. Eng., 12, 59–73, https://doi.org/10.1016/j.jrmge.2018.12.018, 2020.
Rajendran, K., Parameswaran, R. M., and Rajendran, C. P.: Seismotectonic perspectives on the Himalayan arc and contiguous areas: Inferences from past and recent earthquakes, Earth-Sci. Rev., 173, 1–30, https://doi.org/10.1016/j.earscirev.2017.08.003, 2017.
Rawat, M. S., Joshi, V., Uniyal, D. P., and Rawat, B. S.: Investigation of hill slope stability and mitigation measures in Sikkim Himalaya, Int. J. Landslide Environ., 3, 8–15, 2016.
Sarkar, S. and Kanungo, D. P.: Landslides in the Alaknanda Valley of Garhwal Himalaya, India, Q. J. Eng. Geol. Hydroge., 39, 79–82, https://doi.org/10.1144/1470-9236/05-020, 2006.
Sati, S. P., Sundriyal, Y., Rana, N., and Dangwal, S.: Recent landslides in Uttarakhand: nature's fury or human folly, Curr. Sci. India, 100, 1617–1620, 2011.
Schwanghart, W. and Scherler, D.: Short Communication: TopoToolbox 2 – MATLAB-based software for topographic analysis and modeling in Earth surface sciences, Earth Surf. Dynam., 2, 1–7, https://doi.org/10.5194/esurf-2-1-2014, 2014.
Schwanghart, W. and Scherler, D.: Bumps in river profiles: uncertainty assessment and smoothing using quantile regression techniques, Earth Surf. Dynam., 5, 821–839, https://doi.org/10.5194/esurf-5-821-2017, 2017.
Schwanghart, W., Molkenthin, C., and Scherler, D.: A systematic approach and software for the analysis of point patterns on river networks, Earth Surf. Proc. Land., 46, 1847–1862, https://doi.org/10.1002/esp.5127, 2021.
Sharma, A. K., Parkash, S., and Roy, T. S.: Response to Uttarakhand disaster 2013, International Journal of Scientific and Engineering Research, 5, 1251–1256, 2014.
Shugar, D. H., Jacquemart, M., Shean, D., Bhushan, S., Upadhyay, K., Sattar, A., Schwanghart, W., McBride, S., van Wyk de Vries, M., Mergili, M., Emmer, A., Deschamps-Berger, C., McDonnell, M., Bhambri, R., Allen, S., Berthier, E., Carrivick, J. L., Clague, J. J., Dokukin, M., Dunning, S. A., Frey, H., Gascoin, S., Haritashya, U. K., Huggel, C., Kääb, A., Kargel, J. S., Kavanaugh, J. L., Lacroix, P., Petley, D., Rupper, S., Azam, M. F., Cook, S. J., Dimri, A. P., Eriksson, M., Farinotti, D., Fiddes, J., Gnyawali, K. R., Harrison, S., Jha, M., Koppes, M., Kumar, A., Leinss, S., Majeed, U., Mal, S., Muhuri, A., Noetzli, J., Paul, F., Rashid, I., Sain, K., Steiner, J., Ugalde, F., Watson, C. S., and Westoby, M. J.: A massive rock and ice avalanche caused the 2021 disaster at Chamoli, Indian Himalaya, Science, 373, 300–306, https://doi.org/10.1126/science.abh4455, 2021.
Siddique, T. and Pradhan, S. P.: Stability and sensitivity analysis of Himalayan road cut debris slopes: an investigation along NH-58, India, Nat. Hazards, 93, 577–600, https://doi.org/10.1007/s11069-018-3317-9, 2018.
Siddique, T., Pradhan, S. P., Vishal, V., Mondal, M. E. A., and Singh, T. N.: Stability assessment of Himalayan road cut slopes along National Highway 58, India, Environ. Earth Sci., 76, 1–18, 2017.
Singh, R., Umrao, R. K., and Singh, T. N.: Stability evaluation of road-cut slopes in the Lesser Himalaya of Uttarakhand, India: conventional and numerical approaches, B. Eng. Geol. Environ., 73, 845–857, 2014.
Stanley, T. and Kirschbaum, D. B.: A heuristic approach to global landslide susceptibility mapping, Nat. Hazards, 87, 145–164, https://doi.org/10.1007/s11069-017-2757-y, 2017.
Stead, D.: The Influence of Shales on Slope Instability, Rock Mech. Rock Eng., 49, 635–651, https://doi.org/10.1007/s00603-015-0865-0, 2016.
Sur, U., Singh, P., and Meena, S. R.: Landslide susceptibility assessment in a lesser Himalayan road corridor (India) applying fuzzy AHP technique and earth-observation data, Geomatics, Nat. Hazards Risk, 11, 2176–2209, https://doi.org/10.1080/19475705.2020.1836038, 2020.
Swarnkar, S., Mujumdar, P., and Sinha, R.: Modified hydrologic regime of upper Ganga basin induced by natural and anthropogenic stressors, Sci. Rep.-UK, 11, 1–11, 19491, https://doi.org/10.1038/s41598-021-98827-7, 2021.
Tanyaş, H., Görüm, T., Kirschbaum, D., and Lombardo, L.: Could road constructions be more hazardous than an earthquake in terms of mass movement?, Nat. Hazards, 112, 639–663, https://doi.org/10.1007/s11069-021-05199-2, 2022.
The Tribune, India: https://www.tribuneindia.com/news/nation/10-969-km-roads-in-himalayan-states-461738, last access: 29 December 2022.
United States Geological Survey (USGS): Earthquake Catalog, https://earthquake.usgs.gov/earthquakes/search/, last access: 27 November 2022.
Uniyal, A.: Infra Development Vision for Himalaya in the Aftermath of Rishiganga Tragedy, in: Disaster & Development, Journal of the National Institute of Disaster Management, New Delhi, vol. 10, edited by: Bindal, M. K., Parkash, S., Thapa, R., Kaur, H., and Kathait, A., New Delhi, 149–159, 2021.
van Erp, S., Oberski, D. L., and Mulder, J.: Shrinkage priors for Bayesian penalized regression, J. Math. Psychol., 89, 31–50, https://doi.org/10.1016/j.jmp.2018.12.004, 2019.
van Westen, C. J., Castellanos, E., and Kuriakose, S. L.: Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview, Eng. Geol., 102, 112–131, https://doi.org/10.1016/j.enggeo.2008.03.010, 2008.
Vergani, C., Giadrossich, F., Buckley, P., Conedera, M., Pividori, M., Salbitano, F., Rauch, H., Lovreglio, R., and Schwarz, M.: Root reinforcement dynamics of European coppice woodlands and their effect on shallow landslides: A review, Earth-Sci. Rev., 167, 88–102, https://doi.org/10.1016/j.earscirev.2017.02.002, 2017.
Wadhawan, S. K., Singh, B., and Ramesh, M. V.: Causative factors of landslides 2019: case study in Malappuram and Wayanad districts of Kerala, India, Landslides, 17, 2689–2697, 2020.
Wang, Q., Zhang, P.-Z., Freymueller, J. T., Bilham, R., Larson, K. M., Lai, X., You, X., Niu, Z., Wu, J., Li, Y., Liu, J., Yang, Z., and Chen, Q.: Present-Day Crustal Deformation in China Constrained by Global Positioning System Measurements, Science, 294, 574–577, https://doi.org/10.1126/science.1063647, 2001.







