Overview
Test Series
Integration is the process of finding functions whose derivatives are given. It is called anti-differentiation as we move backward from the differentiated equation. We know about single variable integrals of the form \( \int_a^bf\left(x\right)dx \) which lies in the interval \( \left[a,\ b\right] \). This integral gives the area bounded in the x-y plane under the function \( f\left(x\right)dx \) between \( \left(a,\ 0\right)\ and\ \left(b.\ 0\right) \). Now, if we want to integrate over any curve the area under which is not bounded in a 2D plane then we use a new kind of integral known as Line Integral.
What is Line Integral?
Line integral is a special kind of integration that is used to integrate any curve in 3D space. It extends the familiar procedure of finding the area of flat, two-dimensional surfaces through simple integrals to integration techniques to find the area of surface not bound in a two-dimensional plane. It allows us to integrate multivariable functions and vector fields over arbitrary curves the area under which is not bound to a 2D plane for mensuration 2D area. It is also known as Path Integral as the integration is done along a path.
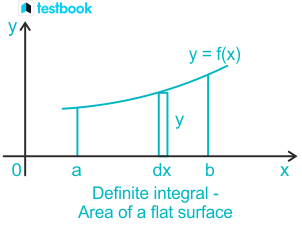

Let us understand this with an example.
In physics, we have a relation, Work=Force x Distance
If we want to find the total amount of work done(W) in moving an object along a curve C in \( R^2 \) having the parametrization, \( x=x\left(t\right),\ y=y\left(t\right),\ a\le t\le b \). The force applied here is \( f\left(x,\ y\right) \) which varies with the position \( \left(x,\ y\right) \) is applied in the direction of motion along C.

We will assume that the function \( f\left(x,\ y\right) \) is continuous and real-valued, so we only consider the magnitude of the force.
Partition the interval \( \left[a,\ b\right] \) as follows:
\( a=t_0<t_1<t_2\ .\ .\ .\ <t_{n-1}<t_n=b \), for some integer \( n\ge2 \)
From the figure, we can say over a typical subinterval \( [t_i,\ t_{i+1}] \) the distance \( \triangle s_i \) traveled along the curve is approximately \( \sqrt{\triangle x_i^2+\triangle y_i^2} \), by pythagoras theorem.
Thus, if the subinterval is small enough then the work done in moving the object along that piece of the curve is approximately,
Force x Distance \( \approx f\left(x_{i\ast},\ y_{i\ast}\right)\sqrt{\triangle x_i^2+\triangle y_i^2} \)
where, \( (x_{i\ast},\ y_{i\ast})=(x(t_{i\ast}),\ y(t_{i\ast})) \) for some \( t_{i\ast} \) in \( [t_i,\ t_{i+1}] \), and so
\( W \approx \sum_{i=0}^{n-1} f (x_{i∗}, y_{i∗}) \sqrt{ ∆x_i^2 +∆y_i^2}\label{} \)
is approximately the total amount of work done over the entire curve. But since \( \sqrt{ ∆x_i^2 +∆y_i^2} = \sqrt{\left ( \dfrac{∆x_i}{∆t_i} \right )^2 +\left ( \dfrac{∆y_i}{∆t_i}\right )^2}∆t_i \)
where \( ∆t_i=t_{i+1}-t_i \), then
\( W \approx \sum_{i=0}^{n-1}f (x_{i∗}, y_{i∗})\sqrt{\left ( \dfrac{∆x_i}{∆t_i} \right )^2 + \left ( \dfrac{∆y_i}{∆t_i} \right )^2}∆t_i \label{} \)
Taking the limit of that sum as the length of the largest subinterval goes to 0, the sum over all subintervals becomes the integral from \( t=a\ to\ t=b \),
\( \triangle x_i\ \triangle t_i\ and\ \triangle y_i\ \triangle t_i\ \) become \( x^{\prime}\left(t\right)\ and\ y^{\prime}\left(t\right) \) respectively, and \( f\left(x_{i\ast},\ y_{i\ast}\right) \), so that
\( W=\int_a^b f (x(t), y(t)) \sqrt{x^′ (t)^2 + y^′ (t)^2}\,dt \label{} \)
The integral on the right side of the above equation gives us an idea of how to define the line integral, for any real-valued function \( f\left(x,\ y\right) \), the integral of \( f\left(x,\ y\right) \) along the curve C.
Learn about Surface Integral

Get 3 Months SuperCoaching @ just
₹1999₹299
Types of Line Integral
Line Integral are of 2 types as mentioned below:
- Line Integral of Vector Field
- Line Integral of Scalar Field
Line Integral of Vector Field
To evaluate a line integral of vector field we will consider this vector field,
\( \vec F\left( {x,y,z} \right) = P\left( {x,y,z} \right)\vec i + Q\left( {x,y,z} \right)\vec j + R\left( {x,y,z} \right)\vec k \)
where, the 3D curve is given by \( \vec r\left( t \right) = x\left( t \right)\vec i + y\left( t \right)\vec j + z\left( t \right)\vec k\hspace{0.25in}\hspace{0.25in}a \le t \le b \)
Then the line integral of \( \vec{F} \) along C is \( \int\limits_{C}{{\vec F\centerdot d\,\vec r}} = \int_{{\,a}}^{{\,b}}{{\vec F\left( {\vec r\left( t \right)} \right)\centerdot \vec {r^{‘}}\left( t \right)\,dt}} \),
where \( \int\limits_{C}{{\vec F\centerdot d\,\vec r}} \) is the dot product of the vector field and differential, and
\( \vec{F}\left(\vec{r}\left(t\right)\right)=\vec{F}\left(x\left(t\right),\ y\left(t\right),\ z\left(t\right)\right) \)
The line integral of the vector field can also be written with respect to arc length, such as
\( \int\limits_{C}{{\vec F\centerdot d\,\vec r}} = \int\limits_{C}{{\vec F\centerdot \vec T\,ds}}
\),
where \( \vec{T}\left(t\right) \) is the unit vector tangent given by,
\( \vec T\left( t \right) = \frac{{\vec r’\left( t \right)}}{{\left\| {\vec r’\left( t \right)} \right\|}} \)
Line Integral of Scalar Field
Line integral of a scalar function can be assumed as a generalization of the one-variable integral of a function over an interval in which the interval can be in the shape of a curve.
A simple analogy that explains scalar line integral is that of calculating the mass of a wire from its density.
If the density of a given wire were constant, then its mass can be calculated by multiplying the density by the arc length of the curve. If, on the other hand, the density changes along the wire, one can use a process similar to that of calculating the arc length to derive a formula for the density.
This formula defines the line integral over the wire of the function giving the density.
We can write the scalar function expression using Riemann sum converge such as,
\( \int_a^bf\left(c\left(t\right)\right)\left|\left|c^{\prime}\left(t\right)\right|\right|dt \).
This is called the line integral of \( f \) over the curve parametrized by c.
- Also Includes
- All Test Series
- Prev. Year Paper
- Practice
- Pro Live Tests
- Unlimited Test Re-Attempts
Line Integral Formula
The formula can be classified according to the types of Line Integral.
Line Integral of Vector Field: The vector formula of Line Integral is given below.
Let us consider a function \( F\ :\ R\ \rightarrow\ R \) and the line integral for a curve towards r can be represented as
\( \int\limits_{C}{{\vec F\centerdot d\,\vec r}} = \int_{{\,a}}^{{\,b}}{{\vec F\left( {\vec r\left( t \right)} \right)\centerdot \vec {r^{‘}}\left( t \right)\,dt}} \)
Line Integral of Scalar Field: If we consider a function \( F\ :\ R\ \rightarrow\ R \), the Line Integral for scalar function can be represented as,
\( \int_C^{ }Fdr=\int_a^bf\left(c\left(t\right)\right)\left|\left|c^{\prime}\left(t\right)\right|\right|dt \)
- 68 Full Test
- 20 Selection Test 🎯
- 148 Chapter Test
- +143 more tests
- 2 AIM IIT 🎯
- 49 Class XI
- 65 Class XII
- 2 Live Test
- 163 Class XI Chapter Tests
- 157 Class XII Chapter Tests
- 32 Full Test
- 25 Selection Test 🎯
- 157 Chapter Test
- +6 more tests
- 74 Previous Year Chapter Test
Line Integral Theorem
Line integral theorem, also known as the gradient theorem, extends the fundamental theorem of calculus to line integrals through a vector field. It states that the line integral of the gradient of a function gives the total change in the value of f from the start of the curve to its end.
The theorem can be represented as,
\( \int_a^b\nabla f\left(\vec{r}\left(t\right)\right)\ .\ \vec{r^{\prime}}\left(t\right)dt\ =\ f\left(\vec{r}\left(b\right)\right)-f\left(\vec{r}\left(a\right)\right) \)
where,
f is a scalar-valued multivariable function,
\( \nabla f \) is the gradient of f,
\( \vec{r}\left(t\right) \) is a vector-valued function that parametrizes some path through the input space of f,
\( \vec{r}\left(a\right)\ and\ \vec{r}\left(b\right)\ \) are the end points the said path,
\( \vec{r^{\prime}}\left(t\right) \) is the derivative of \( \vec{r}\left(t\right) \) which is considered component wise.
This theorem gives us the result that gradient fields are path independent. Thus, the line integrals along any two paths connecting the same start and end points will be equal.
How to Solve Line Integral
The steps to solve Line integral are given below:
- Step 1: First we have to identify the given function f(x, y, z), and also the curve C over which the integration will take place.
- Step 2: We then write the parametric equation of the given curve. It is usually written as x(t), y(t), z(t). This step is also known as parameterization.
- Step 3: Then we calculate ‘ds’ over the determined parametric equation.
- Step 4: Then we put the values in the formula and solve accordingly to get the required solution of the curve.
Applications of Line Integral
Line Integral has vast applications in the field of science and engineering which are given below:
- Scalar Line integrals are used to determine the length or mass of a given wire, the surface area of a sheet of a given height, or the electric potential of a charged wire where linear charge density is given.
- Vector integrals are extremely useful to calculate the work done on a particle as it moves through a force field, or the rate of flow of a fluid across a curve.
- line integrals are also used to determine the exact length of power cable needed to connect two substations which are usually situated miles away from each other.
- Line integrals are also used by space flight engineers for long missions, where While launching exploratory satellites, they consider the path of the different orbiting velocities of Earth and thus calculate required paths.
- They also have applications in determining the velocity and trajectory of an object.
- In chemistry also line integrals are used to calculate the rate of reaction and get the required information regarding radioactive decay reactions.
- The surface area of mensuration 3D based surfaces can also be calculated using line integral.
Solved Examples of Line Integral
Example 1: Evaluate \( \displaystyle \int\limits_{C}{{\sin \left( {\pi y} \right)\,dy\, + \,y{x^2}\,dx}} \) where C is a line segment from \( \left(0,\ 2\right)\ to\ \left(1,\ 4\right) \)
Solution: First we write the parametric equation, such as
\( \vec r\left( t \right) = \left( {1 – t} \right)\left\langle {1,4} \right\rangle + t\left\langle {0,2} \right\rangle = \left\langle {1 – t,4 – 2t} \right\rangle \,\hspace{0.25in}0 \le t \le 1 \)
Now, we solve the integral by putting the values after parametrization.
\( \begin{align*}\int\limits_{C}{{\sin \left( {\pi y} \right)\,dy\, + \,y{x^2}\,dx}} & = \int\limits_{C}{{\sin \left( {\pi y} \right)\,dy\,}} + \int\limits_{C}{{y{x^2}\,dx}}\\ & = \int_{{\,0}}^{{\,1}}{{\sin \left( {\pi \left( {4 – 2t} \right)} \right)\left( { – 2} \right)\,dt}} + \int_{{\,0}}^{{\,1}}{{\left( {4 – 2t} \right){{\left( {1 – t} \right)}^2}\left( { – 1} \right)\,dt}}\\ & = – \left. {\frac{1}{\pi }\cos \left( {4\pi – 2\pi t} \right)} \right|_0^1 – \left. {\left( { – \frac{1}{2}{t^4} + \frac{8}{3}{t^3} – 5{t^2} + 4t} \right)} \right|_0^1\\ & = – \frac{7}{6}\end{align*} \)
Thus \( – \frac{7}{6} \) is the required solution.
Example 2: Evaluate \( \vec F\left( {x,y,z} \right) = 8{x^2}y\,z\,\vec i + 5z\,\vec j – 4x\,y\,\vec k \) and C is the curve given by \( \vec r\left( t \right) = t\,\vec i + {t^2}\,\vec j + {t^3}\,\vec k \), \( 0\le t\le1 \)
Solution: First we need the vector field evaluated along the curve.
So, \( \vec F\left( {\vec r\left( t \right)} \right) = 8{t^2}\left( {{t^2}} \right)\left( {{t^3}} \right)\vec i + 5{t^3}\,\vec j – 4t\left( {{t^2}} \right)\vec k = 8{t^7}\,\vec i + 5{t^3}\,\vec j – 4{t^3}\,\vec k \)
Next, we will find the derivative of the parameterization, such as
\( \vec r’\left( t \right) = \,\vec i + 2t\,\vec j + 3{t^2}\,\vec k \)
Finally, we determine the dot product, such as
\( \vec F\left( {\vec r\left( t \right)} \right)\centerdot \vec r’\left( t \right) = 8{t^7} + 10{t^4} – 12{t^5} \)
Therefore we put all these in the formula and get,
\( \begin{align*}\int\limits_{C}{{\vec F\centerdot d\,\vec r}} & = \int_{{\,0}}^{{\,1}}{{8{t^7} + 10{t^4} – 12{t^5}\,dt}}\\ & = \left. {\left( {{t^8} + 2{t^5} – 2{t^6}} \right)} \right|_0^1\\ & = 1\end{align*} \)
Thus 1 is the required solution.
| If you are checking Line integral article, also check related maths articles: | |
| Simpsons rule | Integration by substitution |
| Riemann integral | Exponent rules |
| l hospital rule | Assumed mean method |
Line Integral FAQs
Sign Up Now &
- Daily Live Classes
- 3000+ Tests
- Study Material & PDF
- Quizzes With Detailed Analytics
- + More Benefits