Construct Different Types of Quadrilaterals
How to construct different types of quadrilaterals?
The different types of quadrilaterals are constructed and classified by relationships of their sides, angles and diagonals.
Some of the constructions of different types of quadrilaterals are given below along with the steps-by-step explanation.
1. Construct
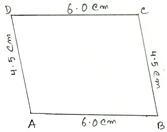
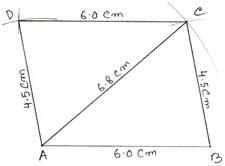
a parallelogram ABCD in which AB = 6 cm, BC = 4.5 cm and diagonal AC = 6.8 cm.
Solution:
Draw a rough sketch of the required parallelogram and write down the given dimensions. (Rough Sketch) →
Steps of Construction:
(i) Draw AB = 6 cm.
(ii) With A as center and radius 6.8 cm, draw an arc.
(iii) With B as center and radius 4.5 cm draw another arc, cutting the previous arc at C.
(iv) Join BC and AC.
(v) With
A as center and radius 4.5 cm, draw an arc.
(vi) With C as center and radius 6 cm draw another arc, cutting the previously drawn arc at D.
(vii) Join DA and DC.
Then, ABCD is the required parallelogram.
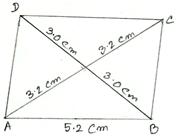
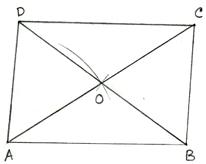
2. Construct a parallelogram, one of whose sides is 5.2 cm and whose diagonals are 6 cm and 6.4 cm.
Solution:
We know that the diagonals of a parallelogram bisect each other.
Make a rough sketch of the required parallelogram, as shown. (Rough Sketch) →
Steps of Construction:
(i) Draw AB = 5.2 cm.
(ii) With A as center and radius 3.2 cm, draw an arc.
(iii) With B as center and radius 3 cm draw another arc, cutting the
previous arc at O.
(iv) Join OA and OB.
(v) Produce AO to C such that OC = AO and produce BO to D such that OD = OB.
(vi) Join AD, BC and CD.
Then, ABCD is the required parallelogram.
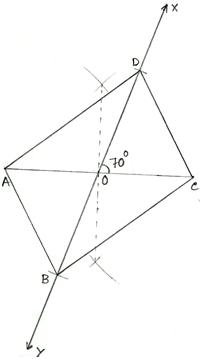
3. Construct a parallelogram whose diagonals are 5.4 cm and 6.2 cm and an angle between them is 70°.
Solution:
We know that the diagonals of a parallelogram bisect each other.
So, we may proceed according to the steps given below.
Steps of Construction:
(i) Draw AC = 5.4 cm.
(ii) Bisect AC at O.
(iii) Make ∠COX =
70° and produce XO to Y.
(iv) Set off OB = 1/2 (6.2) = 3.1 cm and OD = 1/2 (6.2) =3.1 cm as shown.
(v) Join AB, BC, CD and DA.
Then, ABCD is the required parallelogram.
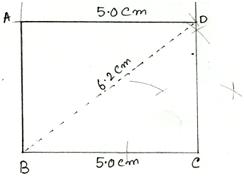
4. Construct a rectangle ABCD in which side BC = 5 cm and diagonal BD = 6.2 cm.
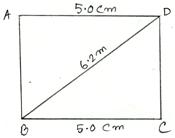
Solution:
First draw a rough sketch of the required rectangle and write down its dimensions.
Now, we may construct it by following the steps given below. (Rough Sketch) →
Steps of Construction:
(i) Draw BC = 5 cm.
(ii) Draw CX ⊥ BC.
(iii) With B as center and radius 6.2 cm draw an arc, cutting CX at D.
(iv) Join BD.
(v) With D as center and radius 5 cm, draw an arc.
(vi) With B as center and radius equal to CD draw another arc, cutting the previous arc at A.
(vii) Join AB and AD.
Then, ABCD is the required rectangle.
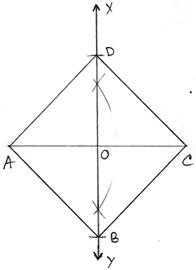
5. Construct a square ABCD, each of whose diagonals is 5.2 cm.
Solution:
We know that the diagonals of a
square bisect each other at right angles.
So, we proceed according
to the following steps.
Steps of Construction:
(i) Draw AC = 5.2 cm. (ii) Draw the right bisector XY of AC, meeting AC at O.
(iii) From O set off OB = 1/2 (5.2) = 2.6 cm along OY and OD = 2.6 cm along OX.
(iv) Join AB, BC, CD and DA.
Then, ABCD is the required square.
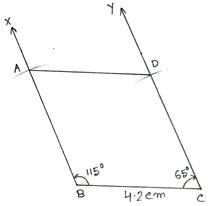
6. Construct a rhombus with side 4.2 cm and one of its angles equal to 65°.
Solution:
Clearly, the adjacent angle = (180° - 65°) = 115°. So, we may proceed according to the steps given below.
Steps of Construction:
(i) Draw BC = 4.2 cm.
(ii) Make ∠CBX = 115° and ∠BCY = 65°.
(iii) Set off BA = 4.2 cm along BX and CD = 4.2 cm along CY.
(iv) Join AD.
Then, ABCD is the required rhombus.
To
construct different types of quadrilaterals students can follow the
explanation given in the steps of the construction of quadrilateral.
● Related Concepts on Quadrilateral
● Different Types of Quadrilaterals
● Construction of Quadrilaterals
● Construct Different Types of Quadrilaterals
● Quadrilateral - Worksheets
● Worksheet on Construction on Quadrilateral
● Worksheet on Different Types of Quadrilaterals
8th Grade Math Practice
From Construct Different Types of Quadrilaterals to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Roman Numerals |Roman Numerals|Symbols for Roman Numerals
Dec 27, 24 09:45 AM
Practice the worksheet on roman numerals or numbers. This sheet will encourage the students to practice about the symbols for roman numerals and their values. Write the number for the following: (a) V… -
Rules for Formation of Roman-Numerals |Roman-numerals System|Worksheet
Dec 25, 24 03:55 PM
In rules for formation of Roman-numerals system there is no symbol or digit for zero. This system has no place value system. The digit or digits of lower value is/are placed after or before the -
3rd Grade Number Worksheet |Practice the Questions on Numbers with Ans
Dec 24, 24 11:46 PM
3rd grade number worksheet will help the kids to practice the questions on numbers. Fill in the blanks: Write in words: Write in numerals: Write > or =, < between the given numbers: -
Expanded Form and Short Form of a Number | Numbers in Expanded Form
Dec 23, 24 02:39 AM
When we write a number as a sum of place value of its digits, the number is said to be in expended form and when we write a number using digits, the number is said to be in short form. There are 3 way… -
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Dec 22, 24 04:09 PM
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If…





New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.