Prerpints.org logo
Preprint
Article

Mechanical Spectroscopy Study of CrNiCoFeMn High Entropy Alloys

Altmetrics

Downloads

136

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 April 2023

Posted:

06 April 2023

You are already at the latest version

Alerts
Abstract
Abstract: The high entropy alloy (HEA) of equiatomic composition CrNiFeCoMn and with FCC 11 crystal structure was prepared by either induction melting and additive manufacturing with a se- 12 lective laser melting (SLM) process, starting from mechanically alloyed powders. Unlike induction 13 melting, the as-produced SLM alloy showed fine nitride and Cr-rich s phase precipitates. Mechan- 14 ical spectroscopy measurements were performed on specimens cold worked and/or recrystallized. 15 Young’s modulus values of (140±10) GPa and (90±10) GPa were measured at 300 K for induction 16 melted and SLM samples, respectively. The values increased to (160±10) GPa and (170±10) GPa for 17 recrystallized samples. Damping measurements as a function of temperature showed two peaks 18 which were attributed to dislocations bending and grain boundaries sliding. The peaks were super- 19 posed on a temperature increasing background.
Keywords: 
Subject: Chemistry and Materials Science  -   Metals, Alloys and Metallurgy

1. Introduction

Two papers were published in 2004 by B. Cantor [1] and J. W. Jeh [2] suggesting a new and completely different set of strategies for developing new materials. Despite the articles did not attract much attention immediately after their publication, they became, in less than a decade, very influential papers. The alloys they reported about were named High Entropy Alloys (HEA) or Cantor’s alloys, after the name of the discoverer. These pioneering studies reported about an equiatomic alloy consisting of the five transition metals Cr, Mn, Fe, Co and Ni crystallized as a single solid solution [1,2,3,4] in the as cast and in the homogenized state.
The first HEAs generation could contain five or more main elements with the concentration of each element in the range 5-35 atomic % [2]. The alloys presented a high mixing entropy in their liquid state [3] and thus could form simple solid solution structures (e.g. FCC, BCC and HCP) in place of intermetallic phases. Some promising technological characteristics of HEAs were high hardness, good wear resistance, excellent strength at both high and low temperatures and generally a good resistance to oxidation and corrosion [5,6,7,8]. The unique properties of the HEAs were ascribed to the inherent properties of multicomponent solid solution formation, such as distorted lattice structures, cocktail effect, sluggish diffusion and formation of nanoscale deformation twins [9].
From a metallurgical standpoint, the suppression of the brittle intermetallic phases in such alloys is to be regarded as a really interesting feature. As recalled by other authors, the CrNiMnCoFe HEAs are considered stable disordered supersaturated FCC solid solutions with high ductility and remarkable fracture toughness [8]. HEAs usually exhibit good thermal stability [6,7,10], which was commonly attributed to sluggish long-range substitutional diffusion because of the lack of a major diffusion element and the need for cooperative diffusion of constituent atoms in order to have proper composition partitioning. Consequently, diffusion-related processes, including re-crystallization and grain growth, are expected to be slow in HEAs.
The belief that the equiatomic CoCrFeNiMn alloy be an HEA example with a single disordered solid solution structure was recently challenged by the discovery of (precipitates) second phases in the alloy after low-temperature annealing. Nitrides and σ phase precipitates inside the grains and at the grain boundaries are present and, together with twins and other defects, influence the mechanical properties of these alloys. In fact, precipitates could lead to relevant changes in the alloy mechanical properties, either increasing the strength or embrittling the alloy. In both cases it is important to control the new phase precipitation or dissolution upon heat treatment. Furthermore, it was proved that secondary phases may contribute significantly to the HEAs properties, and it was reported that HEAs can overcome the strength-ductility trade-off when containing two or more phases [11,12].
A number of studies in recent years have been aimed at determining the mechanical properties of these alloys [13,14,15,16,17,18]. In particular, Yield strength, Hardness, Fracture toughness, Strain hardening and Elastic constants were measured for alloys of various compositions and subjected to a number of thermal and mechanical treatments. As far as the elastic constants are concerned, the experimental measurements were mainly aimed at measuring the Young's modulus and Shear modulus, mostly using resonant ultrasound spectroscopy techniques, stress-strain tests and nanoindentation. Very few data are instead related to Mechanical Spectroscopy (MS) measurements. With this technique, damping and the Young's Modulus are measured dynamically and non-destructively [19,20]. Damping is defined as the capacity of a material to convert vibrational mechanical energy into heat. During a MS test, damping is usually measured together with the Young's modulus and the values thus obtained are usually more precise than those obtained by static or indentation measurements. The measure of damping, also named internal friction, is highly sensitive to the various features of the material microstructure, such as dislocations, grain boundaries, precipitates and internal stress and therefore provides information on the microstructure that is difficult to obtain in any other way.
Aim of this article is to present MS measurements obtained on Cantor’s alloys of CrNiMnCoFe composition prepared in two different ways, as described below, deformed by cold rolling and re-crystallized. Specifically, the temperature-dependent damping and Young’s elastic modulus of two alloys produced by induction melting and laser melting were measured and correlated with their different microstructure. The test equipment is of the resonant bar type, that is the specimen is mounted in single cantilever mode and it is excited to its first longitudinal vibration mode by applying an alternating voltage. Resonances in the acoustic range are obtained. By changing the temperature, it was therefore possible to study thermally activated processes such as those due to dislocations bending and grain boundaries sliding.

2. Materials and Methods

As reported in greater details in previous articles [21,22], a nominally equiatomic HEA was produced by two different processes. In the first, and more standard process, Co, Cr, Fe, Mn and Ni powders, supplied by Sigma Aldrich (Darmstadt, Germany), with purity greater than 97 % at., were subjected to pre-alloying by mechanical milling in Argon atmosphere using a Planetary Ball Mill (PM 100 by Retsch GmbH, steel balls with BPR 15:1, Haan, Germany) working at 400 rpm. Treatment cycles lasting 15 minutes each with a 5 minutes break between them for a total grinding time of 45 hours were used. Break time was used to avoid overheating. The alloyed powders were placed in alumina crucibles and thermally treated in a vacuum induction furnace at temperatures exceeding 1720 K for 30 min, during which complete melting was achieved. Disks with 35 mm diameter and 8 mm height were produced. They weighted between 56 g and 58 g. Induction melting of mechanically pre-alloyed powders was used as a synthesis approach in order to reduce element segregation and Mn loss. Sections of the as-cast disks were cold rolled using a laboratory rolling equipment to achieve a 90% thickness reduction (from 3 mm to 0.3 mm). Some of the cold rolled specimens were subsequently re-crystallized by a 30 min annealing at 1173 K in a Kanthal Super HT rapid high-temperature furnace (Hallstahammar, Sweden). Samples density was ρ = (7.1±0.2) g/cm3, without any significant difference between as cast and annealed samples.
In the second process, the same starting mechanically pre-alloyed powders were melted by selective laser melting (SLM) in additive manufacturing [23,24]. The SLM apparatus, used to produce samples with volume 50x5x5 mm3, was a SISMA MYSINT100 RM (Vicenza, Italy). A high purity Nitrogen atmosphere was used in order to minimize oxidation during the production process. Melting did not take place until Oxygen level dropped below the set limit threshold, which was 0.5%. The samples surface perpendicular to the growth direction was divided into 6 slices filled according to a chessboard strategy [25]. Again, sections of the starting material were cold rolled with a 90% thickness reduction and re-crystallized by a 30 min annealing at 1173 K. Samples density was ρ = (7.0±0.1) g/cm3, ρ = (7.1±0.1) g/cm3, before and after re-crystallization, respectively.
As-cast, cold-worked and re-crystallized specimens were analyzed as follows:
a)
Micro-structural investigations. They were performed by optical microscopy with an Olympus GX71 (Tokyo, Japan) and electron microscopy using a Tescan MIRA3 (Brno, Czech Republic) equipped with EDS (energy dispersive spectroscopy) microanalyzer by Bruker Quantax (Billerica, MA, USA). Specimens used for these analyses were polished and chemically etched (glyceregia solution composed of 1 HNO3 + 3 HCl + 3 Glycerol). Crystallographic orientation and grain size were analyzed by electron backscattered diffraction (EBSD). EBSD maps were conducted with Quantax EBSD detector on as built, cold deformed, annealed and re-crystallized samples to document the FCC matrix alloy and the precipitation of secondary phases. The EBSD data were recorded and analysed using the Bruker Esprit software.
b)
X-ray Diffraction (XRD). In order to determine the crystal structure, a Q/2Q scan was performed in the 2Q range from 35 to 100 degrees using a Panalytical X’Pert PRO diffractometer equipped with a gas proportional detector (Malvern, UK). A parallel beam configuration was applied, including an X-ray mirror (incident beam optics) coupled with a long soller slit and a flat monochromator (diffracted beam optics). Hence, sample displacement errors were avoided, and a correct determination of the unit cell from peak positions could be performed.
c)
Mechanical spectroscopy. Damping and dynamic modulus measurements were performed in a vacuum by means of the mechanical analyser VRA 1604 [26,27]. In the VRA apparatus, specimens are mounted in free-clamped mode and excited by flexural vibrations. Specimens were kept into resonance while temperature changed at the selected rate. The resonance frequency of all specimens was in the 300 to 1000 Hz range; the strain amplitude was about 10−5. Specimens were heated from room temperature up to a maximum temperature of 800 K at 1.5 K/min rate. The reeds were put into resonance by an electrostatic excitation and the damping parameter (usually referred to as Q−1) has been determined from the logarithmic decay of the flexural vibrations when excitation was turned off:
Q − 1 = 1 m π l n ⁡ ( A n A n + m )
being An and An+m the amplitudes of the n-th and (n + m)-th oscillation. The dynamic modulus E was obtained from the resonance frequency f, by:
E = 48 π 2 P L m 4 h 2 f 2
where m is a constant (m = 1.875), Ρ the material density, L and h the length and thickness of the sample. Debye relaxation peaks occur when the following condition is satisfied:
ω τ = ω τ 0 e x p ⁡ ( H k T ) = 1
being ω = 2πf, τ the relaxation time, τ0 its pre-exponential factor, H the activation energy of the physical process originating the peak, k the Boltzmann constant and T the temperature.

3. Results

As reported into the introduction, Mechanical Spectroscopy measurements obtained on Cantor’s alloys of CrNiMnCoFe composition prepared in two different ways, in deformed state by cold rolling and in re-crystallized state, were compared. Cold working was used to increase strength and promote re-crystallization, as it is commonly done for alloyed austenitic stainless steels [28], which chemically and mechanically resemble Cantor’s alloys. The improvement in mechanical properties such as hardness, fatigue strength, tensile strength so obtained, were predominantly due to the induction of compressive residual stress in the specimens [22].
Typical damping and dynamic modulus curves of CrNiMnCoFe produced by standard process are reported in Figure 1. The curves of Figure 1 refer to laminated but not re-crystallized samples. The experimental values reported in magenta and red refer to a first thermal run, while those in black and gray refer to a second run on the same sample. In the first run, as regards the damping, the presence of a dissipation peak was observed at T = 400 K, together with a growing background, with Q−1 value at T = 300 K of about 7.5⋅10-4 which grows up to 18⋅10-4 at 700 K. Similar values are commonly measured in many steels and superalloys [20, chapter 4]. This peak was observed in all laminated samples, both standard and SLM. It disappeared completely after heating above 700 K. The dynamic modulus curve (normalized to the initial value, M0, at room temperature) showed a slope change in correspondence of the Q−1 peak, superimposed on a monotonous decreasing trend. It is the modulus relaxation accompanying a peak due to an anelastic effect [19, chapter 1].
The 2nd run revealed how heating during the 1st run, here up to 700 K, up to 800 K in other trials, yielded a damping decrease. This is a commonly observed relaxation effect [19 chapter 11 and 13, 29] due to the internal stresses release caused by the heat treatment. The damping at T=300 K decreased to 4⋅10-4. Quite interesting is the disappearance of the peak at T= 400 K, which is evidently linked to microstructural features of the material capable of being modified with heat treatments at relatively low temperatures. The same effect was also evident in the elastic modulus (normalized to the initial value, as in the 1st run), in which no modulus deficit appeared anymore. The behavior displayed in the 2nd run was stable, in the sense that further heating up to 800 K did not induce changes in the Q−1 and elastic modulus trends.
Figure 2 shows the damping data of Figure 1, analyzed in terms of an exponential increasing background and a Debye peak. In order to determine the peak temperature and apparent activation energy, experimental Q−1 data have been fitted by considering a Debye peak described by the expression:
Q − 1 = ∆ ∙ s e c h ( H k ) ∙ ( 1 T − 1 T p )
being k the Boltzmann constant, ∆ the relaxation strength, H the activation energy and TP the peak position.
To the Debye peak it was added a background described by:
Q − 1 = A + B ∙ e x p ⁡ ( T C )
where A represents the temperature-independent damping term. In Table 1, the values of the fit parameters used for the Debye peak plus background are reported. The relaxation strength is ∆ = 2 ∙ 10 − 4 , with activation energy H = 0.5 ± 0.1 e V (~48 kJ/mol). An evaluation of the activation energy of the peak by means of the displacement of its maximum as a function of the frequency [19, chapter 3] was not accomplished due to the lack of data from samples having a sufficiently wide range of resonance frequencies.
A continuous damping contribution, often increasing exponentially with temperature, is measured in several metals. This background, on which peaks of various origin may be superposed, is higher in cold worked samples while decreases with grain size increase and after annealing at high temperatures. Despite some still controversial points, it is commonly accepted that the increasing background be the result of the contribution of a broad spectrum of diffusion-controlled relaxation processes [30,31]. As to which objects give raise to the relaxation, grain boundaries and dislocations interacting with point defects are considered to give the most significant contributions.
A typical damping and dynamic modulus curve of a standard CrNiMnCoFe specimen after re-crystallization are reported in Figure 3. The behavior is qualitatively the same as that of not-recrystallized samples after a first thermal run above 700 K. Q-1 is monotonously increasing with temperature and no peaks are visible. Both damping and modulus are stable and display the same behavior in successive runs up to 800 K.
The elastic modulus decrease as a function of temperature (about 17% in the 300 to 800 K range) was comparable to the case of the 2nd run of the not-recrystallized sample. However, its absolute value increased with respect to the case of not re-crystallized samples, with E = (140±10) GPa in the case of not re-crystallized samples and E = (160±10) GPa in the case of re-crystallized samples (room temperature values). The anisotropy of the elastic modulus and the texture change during re-crystallization, may be responsible for this increase [32], together with dislocation annihilation.
Let’s now take into consideration samples produce by SLM. The temperature behavior for T < 600 K in a 1st run was the same as that reported in Figure 1 for the standard alloy. In both kind of samples, it was detected a peak which disappeared after the first thermal heating, leading to a reduced background and a stable behavior in subsequent runs. Significant differences appeared in a 2nd run, as shown in Figure 4, where data relating to both a not re-crystallized (black and gray) and a re-crystallized (magenta and red) sample are reported. The comparison between samples already heated up to 800 K is significant because it allows to compare stable structures, at least in the temperature range used for the test. In the not re-crystallized sample, a damping peak appeared at 685 K, superimposed on the usual growing background. The peak was stable when heating up to 800 K, but disappeared after re-crystallization, as shown (magenta data) in Figure 4. The re-crystallization treatment also yielded a more relaxed structure than that of samples treated only up to 800 K. A considerable difference was also measured in the elastic modulus, which increases from the relatively low value E = (90±10)) GPa in the not-recrystallized sample, to E = (170±10)) GPa in the recrystallized one. The relatively low value measured in the SLM samples before re-crystallization was probably due to a microscopic and widespread porosity brought about by melting followed by rapid cooling, as already observed experimentally and modeled in other materials [33,34]. Diffusion and grain boundaries rearrangement during re-crystallization modified the elastic modulus, raising its value towards the standard values. Figure 5 shows the damping curves of the re-crystallized sample of the previous figure, analyzed as before in terms of an exponential increasing background and a Debye peak. In Table 1, the fitting parameters values are reported. The activation energy of this new peak, determined as before, turns out to be H = 1.3 ± 0.1 e V (~127 kJ/mol).
In Figure 6 it is reported the diffraction pattern on an SLM sample after re-crystallization. Peaks corresponding to the FCC phase of the Cantor’s alloy were detected, together with those of the precipitated phases. Precipitates were already present in the as made material. The small size of these precipitates, however, did not provide a sufficient scattering volume to allow this phase to be detected by XRD diffraction. In the re-crystallized material precipitates increased in size, and decreased in number, and became therefore visible. Figure 7 shows the microstructure of a standard sample, before and after recrystallization. No precipitates were observed in standard samples. Instead, they were detected in samples produced by SLM, as can be seen in Figure 8. Note how after re-crystallization, both in the standard and in the SLM sample, there was a widespread presence of geminates, together with a transition from elongated to more rounded grains, Figure 7b and Figure 8d.

4. Discussion

4.1. Low temperature peak of CoCrFeMnNi alloy after cold rolling, without re-crystallization.

Even though, in order to explain the damping capacity and the observed features of these alloys, it is important to examine how process parameters affect the microstructure, there are limited experimental data available in this regard. In this work, the same starting mechanically pre-alloyed powders were used both for the standard fusion and the SLM process. For the latter, it was expected that the mechanical behavior would be affected by the stress field due to the SLM process. At the same time, the local heating under the stressed condition was expected to cause strain relaxation in the surrounding areas. Further stress relaxation was mainly caused by an oriented slip of dislocations, by cold-rolling and successive re-crystallization, which transformed elastic residual strains into microplastic strains.
As regard the peak exhibited by cold worked specimens in their 1st thermal run, it could be attributed to a dislocation-related relaxation, that is to the bending of dislocations under the effect of the applied stress. Dislocation effects were often shown up in plastically deformed alloys because of the high dislocation density. A number of pinning points (vacancy and atoms of different size in the Cantor’s alloy lattice) anchor dislocations, which bow under the applied stress. The result of dislocations bowing is in many cases a damping maximum. Specifically, it is tempting to attribute this low temperature peak to a Bordoni relaxation, since it exhibits some features typical of this relaxation. [35]. A Bordoni relaxation can usually be fit as a Debye peak in the framework of the standard anelastic solid, as we were able to do for our experimental data. The peak appeared at a relatively low temperature. Finally, its strength was of the correct order. The detailed mechanism giving rise to this peak involve a thermally activated formation of double kinks along dislocations, but despite many attempts, there is no complete agreement in the literature on the mechanism and also in this case further measurements would be necessary to remove uncertainty on the peak attribution. In any case, a treatment above 700 K was always enough to get rid of the peak, evidently since this temperature induced a microstructure relaxation that modified the dislocations pinning dynamics. This was evident in the data reported in Figure 2, where, apart from the peak, the sample damping capacity of the 2nd run was definitely below that of the 1st run.
The higher damping in cold worked samples with respect to that of annealed sample was due to the introduction of compressive residual stress during rolling. In addition, a higher dislocation density inside the micro-twins, which was the plastic deformation mechanism of the Cantor HEA and the elongated grain boundaries (affected by cold-rolling) contributed to this increase. Dislocations density and distribution control the overall damping of these alloys at low temperatures [36]. This was observed, as expected, in both standard and SLM specimens, see Figure 2 and Figure 4. The twin formation inside the FCC structure and their subsequent annealing were the main factors that changed the microstructure of the alloy.

4.1. High temperature peak of CoCrFeMnNi alloy produced by SLM after cold rolling and re-crystallization.

In a polycrystalline material, a possible source of attenuation is provided by the movement of grain boundaries. The effect was first proposed by Zener in 1941 [37] and relaxation phenomena occurring along grain boundaries have been studied since then by several authors [38]. The mechanism is that of an anelastic strain due to grain boundaries sliding between adjacent crystals under the action of shear stress. Triple points provide the back stress which restore the boundaries when stress is removed. This basic mechanism can be convoluted by the staking of dislocations at the grain boundaries, particularly in the case of cold worked materials or when the sample thickness is of the same order of the grain diameter.
It has been suggested that precipitates can provide an alternative mechanism to triple points in grain boundaries damping [39]. The proposed model is able to reasonably well describe experimental data taken in several alloys containing precipitates and has a mechanical analogy with a dashpot with three elements in parallel: one spring for the total sliding strain due to the elastic grains deformation, one dashpot for the intrinsic viscosity of a particle-free planar boundary and, finally, two dashpots in series for the sliding viscosity of grain boundaries containing particles, where the sliding across these particles is accommodated by boundary or volume diffusion [38]. As described more extensively in a previous work [22], fine σ phase (body-centered tetragonal lattice) precipitates were present in a specimen produced by SLM. These precipitates were clearly visible in the BSE high resolution image of Figure 8b, together with even smaller precipitates visible in the SEM FEG high resolution image of Figure 8c. The latter were nitrides, around which σ phase precipitates with nanometric size grew. This arrangement, with σ phase growing around nitrides, suggests that at first nitrides appear and then the σ phase is formed by heterogeneous nucleation. These precipitates were absent or in any case greatly reduced in number in the standard samples. This was the main microstructural difference between the two kind of samples.
The not re-crystallized samples produced by SLM exhibited a damping peak just below 700 K. This peak could therefore be due to grain boundaries sliding controlled by precipitates. The peak was indeed observed in the polycrystalline material as produced and disappeared after a re-crystallization treatment, which brought about both a reduction in the grain boundaries surface (grain growth) and in the number and dimension of the precipitates, see Figure 8. Likewise, the peak was not observed in the standard Cantor’s alloy, where precipitates were rare or missing. The measured activation energy (127 kJ/mol) was compatible with that usually measured in grain boundaries peaks. Nonetheless, data currently available were not enough to attribute unambiguously the peak to a specific process and further measurements will be done to this purpose in the future.

4. Conclusions

  • In this work, a mechanical spectroscopy study of two CrNiFeCoMn Cantor’s alloys obtained by induction melting (standard) and by selective laser melting (SLM), with the same lattice structure (FCC), was performed.
  • Both types of alloys, cold-deformed by rolling, showed damping peaks in the 300-800 K temperature range.
  • Cold-worked samples exhibited a damping peak at 400 K with relaxation strength 2 ⋅10-4 and apparent activation energy of 48 kJ/mol. The peak was tentatively attributed to a Bordoni relaxation, that is to dislocation motion. It disappeared after a thermal treatment above 700 K.
  • SLM alloys samples exhibited a damping peak at 685 K with relaxation strength 7.6 ⋅10-4 and apparent activation energy of 127 kJ/mol. The peak was tentatively attributed to grain boundary sliding controlled by precipitates (nitride and σ phase). The peak disappeared after a re-crystallization treatment.
  • An exponentially growing damping background was measured in both standard and SLM samples, with typical values of about 3-5⋅10-4 at 300 K and 20⋅10-4 at 800 K.
  • The dynamic Young’s Modulus of SLM samples was rather low, (90±10) GPa, in the not-recrystallized case, due to porosity. It grew to (170±10) GPa after re-crystallization.

Author Contributions

Conceptualization, E.G.C and. A.C.; formal analysis, E.G.C and. A.C.; investigation, A.C.; resources, A.C.; writing—original draft preparation, A.C; writing—review and editing, E.G.C.; All authors have read and agreed to the published version of the manuscript.”

Funding

This research received no external funding

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
  2. Yeh, J.-W.; Chen, S.K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
  3. Miracle, D.B.; Senkov, O.N.; Wilks, J. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
  4. Cantor, B. Multicomponent high-entropy Cantor alloys. Prog. Mater. Sci. 2021, 120, 100754. [Google Scholar] [CrossRef]
  5. Kao, Y.-F.; Chen, T.-J.; Chen, S.-K.; Yeh, J.-W. Microstructure and mechanical property of as-cast, -homogenized, and -deformed AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys. J. Alloys. Compd. 2009, 488, 57–64. [Google Scholar] [CrossRef]
  6. Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
  7. Tabachnikova. ; Podolskiy,.; Laktionova, M.; Bereznaia, N.; Tikhonovsky, M.; Tortika, A. Mechanical properties of the CoCrFeNiMnVx high entropy alloys in temperature range 4.2–300 K. J. Alloy. Compd. 2017, 698, 501–509. [Google Scholar] [CrossRef]
  8. Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef]
  9. Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
  10. Bhattacharjee, P.P.; Sathiaraj, G.D.; Zaid, M.; Gatti, J.R.; Lee, C.; Tsai, C.W.; Yeh, J.W. Microstructure and texture evolution during annealing of equiatomic CoCrFeMnNi high-entropy alloy. J. Alloys Compd. 2014, 587, 544–552. [Google Scholar] [CrossRef]
  11. Liu, W.; Lu, Z.; He, J.; Luan, J.; Wang, Z.; Liu, B.; Liu, Y.; Chen, M.; Liu, C. Ductile CoCrFeNiMox high entropy alloys strengthened by hard intermetallic phases. Acta Mater. 2016, 116, 332–342. [Google Scholar] [CrossRef]
  12. He, J.Y.; Wang, H.; Huang, H.L.; Xu, X.D.; Chen, M.W.; Wu, Y.; Liu, X.J.; Nieh, T.G.; An, K.; Lu, Z.P. A precipitation-hardened high-entropy alloy with outstanding tensile properties. Acta Mater. 2016, 102, 187–196. [Google Scholar] [CrossRef]
  13. Gludovatz, B.; George, E.P.; Ritchie, R.O. Processing, Microstructure and Mechanical Properties of the CrMnFeCoNi High-Entropy Alloy. JOM 2015, 67, 2262–2270. [Google Scholar] [CrossRef]
  14. Haglund, A.; Koehler, M.; Catoor, D.; George, E.; Keppens, V. Polycrystalline elastic moduli of a high-entropy alloy at cryogenic temperatures. Intermetallics 2015, 58, 62–64. [Google Scholar] [CrossRef]
  15. Zhang, G.; Yang, X.; Qi, W.; Li, Y.; Wang, W.; Chen, Y.; Li, J.; Li, L. Effect of Co on phase stability and mechanical behavior of CoxCrFeNiMnAl0.3 high entropy alloys with micro/nano hierarchical structure. Mater. Des. 2022, 215, 110442. [Google Scholar] [CrossRef]
  16. Laplanche, G.; Kostka, A.; Horst, O.M.; Eggeler, G.; George, E.P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Mater. 2016, 118, 152–163. [Google Scholar] [CrossRef]
  17. Zaddach, A.J.; Niu, C.; Koch, C.C.; Irving, D.L. Mechanical Properties and Stacking Fault Energies of NiFeCrCoMn High-Entropy Alloy. JOM 2013, 65, 1780–1789. [Google Scholar] [CrossRef]
  18. George, E.P.; Curtin, W.A.; Tasan, C.C. High Entropy Alloys: A Focused Review of Mechanical Properties and Deformation Mechanisms. Acta Mater. 2020, 188, 435–474. [Google Scholar] [CrossRef]
  19. Nowick, A.S.; Berry, B.S.; Katz, J.L. Anelastic Relaxation in Crystalline Solids, (Academic Press, New York, 1972).
  20. Blanter, M.S.; Golovin, I.S.; Neuhäuser, H.; Sinning, H.-R. Internal Friction in Metallic Glasses, Springer Series in Materials Science, January, 2007.
  21. Biswas, M.R.; Alzubaidi, M.S.; Shah, U.; Abd-Alrazaq, A.A.; Shah, Z. The Effect of Zr Addition on Melting Temperature, Microstructure, Recrystallization and Mechanical Properties of a Cantor High Entropy Alloy. Materials 2021, 14, 5994. [Google Scholar] [CrossRef]
  22. Campari, E.G.; Casagrande, A. Microstructural Study of CrNiCoFeMn High Entropy Alloy Obtained by Selective Laser Melting. Materials 2022, 15, 5544. [Google Scholar] [CrossRef] [PubMed]
  23. Olakanmi, E.O.T.; Cochrane, R.F.; Dalgarno, K.W. A review on selective laser sintering/melting (SLS/SLM) of aluminium alloy powders: Processing, microstructure, and properties. Prog. Mater. Sci. 2015, 74, 401–477, ISSN 0079-6425. [Google Scholar] [CrossRef]
  24. Rao, H.; Giet, S.; Yang, K.; Wu, X.; Davies, C.H. The influence of processing parameters on aluminium alloy A357 manufactured by Selective Laser Melting. Mater. Des. 2016, 109, 334–346. [Google Scholar] [CrossRef]
  25. Carter, L.N.; Martin, C.; Withers, P.J.; Attallah, M.M. The influence of the laser scan strategy on grain structure and cracking behaviour in SLM powder-bed fabricated nickel superalloy. J. Alloy. Compd. 2014, 615, 338–347. [Google Scholar] [CrossRef]
  26. Bonetti, E.; Campari, E.G.; Pasquini, L.; Savini, L. Automated resonant mechanical analyzer. Rev. Sci. Instruments 2001, 72, 2148–2152. [Google Scholar] [CrossRef]
  27. Amadori, S.; Campari, E.; Fiorini, A.; Montanari, R.; Pasquini, L.; Savini, L.; Bonetti, E. Automated resonant vibrating-reed analyzer apparatus for a non-destructive characterization of materials for industrial applications. Mater. Sci. Eng. A 2006, 442, 543–546. [Google Scholar] [CrossRef]
  28. Norton, R.L. Machine Design—an Integrated Approach (Pearson Education Asia, 2nd edition, 2010).
  29. Li, S.; Deng, L.; Wu, X. The mechanism investigation of deep cryogenic treatment on high alloy martensitic steel by low frequency internal friction. Cryogenics 2010, 50, 433–438. [Google Scholar] [CrossRef]
  30. Rivière, A. Analysis of the low frequency damping observed at medium and high temperatures. Mater. Sci. Eng. A 2004, 370, 204–208. [Google Scholar] [CrossRef]
  31. Povolo, F.; Hermida, E.B. On the Frequency Dependence of the High Temperature Background. 1996, 06, C8–227. [CrossRef]
  32. Szenes, G.; Havancsák, K.; Nagy, E. Young's modulus change during recrystallization. Phys. Status solidi (a) 1974, 22, 125–132. [Google Scholar] [CrossRef]
  33. Boccaccini, A.; Ondracek, G.; Mazilu, P.; Windelberg, D. On the Effective Young's Modulus of Elasticity for Porous Materials: Microstructure Modelling and Comparison Between Calculated and Experimental Values. J. Mech. Behav. Mater. 1993, 4, 119–128. [Google Scholar] [CrossRef]
  34. Kováčik, J. Correlation between Young's modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
  35. Seeger, A. Progress and problems in the understanding of the dislocation relaxation processes in metals. Mater. Sci. Eng. A 2004, 370, 50–66. [Google Scholar] [CrossRef]
  36. Suresh, N.; Ramamurty, U. Aging response and its effect on the functional properties of Cu–Al–Ni shape memory alloys. J. Alloy. Compd. 2008, 449, 113–118. [Google Scholar] [CrossRef]
  37. Zener, C. Theory of the Elasticity of Polycrystals with Viscous Grain Boundaries. Phys. Rev. 1941, 60, 906–908. [Google Scholar] [CrossRef]
  38. Povolo, F.; Molinas, J.B. Present State of the Controversy about the Grain Boundary Relaxation. Il Nuovo Cimento, 1992, 14, 287–332. [Google Scholar] [CrossRef]
  39. Mosher, D.; Raj, R. Use of the internal friction technique to measure rates of grain boundary sliding. Acta Met. 1974, 22, 1469–1474. [Google Scholar] [CrossRef]
Preprints 70530 g001
Figure 1. Q−1 and Young’s dynamic modulus, M, of a standard Cantor’s alloy. First (magenta and red) and second (black and grey) run. Dynamic modulus normalized to its starting value at 300 K, that is (140±10) GPa at the beginning of 2nd run and slightly less than that at the beginning of 1st run. Room temperature frequency: 524 Hz.
Figure 1. Q−1 and Young’s dynamic modulus, M, of a standard Cantor’s alloy. First (magenta and red) and second (black and grey) run. Dynamic modulus normalized to its starting value at 300 K, that is (140±10) GPa at the beginning of 2nd run and slightly less than that at the beginning of 1st run. Room temperature frequency: 524 Hz.
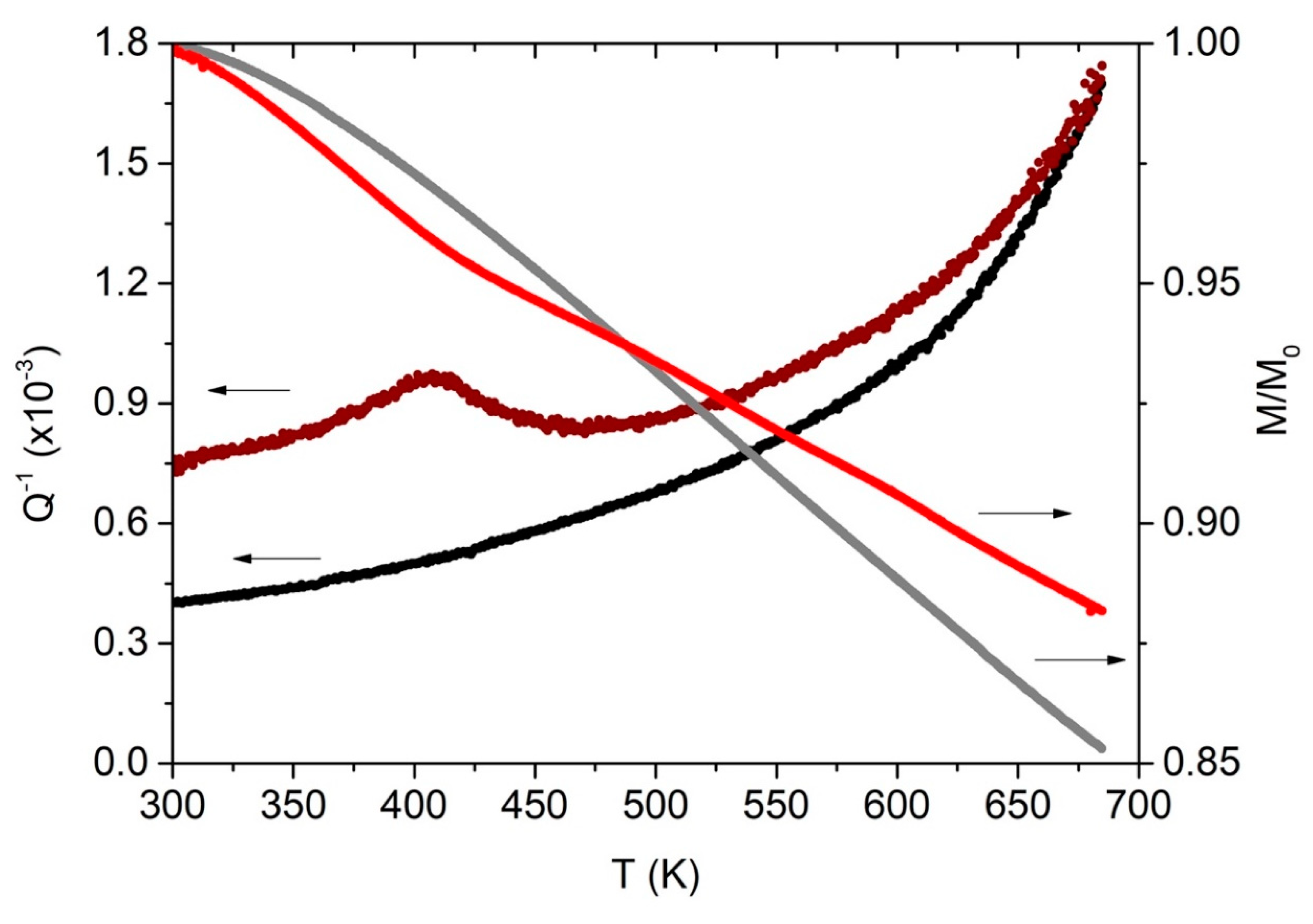
Preprints 70530 g001
Preprints 70530 g002
Figure 2. Q−1 of the standard Cantor’s alloy of Figure 1, analyzed in terms of an exponentially growing background and a Debye peak. The red line superposed to the experimental data (magenta) is the sum of the Debye peak (orange) and the exponential background (olive). The Green curve is an exponential fit of 2nd run Q−1 data (black).
Figure 2. Q−1 of the standard Cantor’s alloy of Figure 1, analyzed in terms of an exponentially growing background and a Debye peak. The red line superposed to the experimental data (magenta) is the sum of the Debye peak (orange) and the exponential background (olive). The Green curve is an exponential fit of 2nd run Q−1 data (black).
Preprints 70530 g002
Preprints 70530 g003
Figure 3. Q-1 (black) and Young’s dynamic modulus (green) of a standard Cantor’s alloy after re-crystallization. Dynamic modulus normalized to its starting value at 300 K, that is E = (160±10) GPa. Room temperature frequency: 352 Hz.
Figure 3. Q-1 (black) and Young’s dynamic modulus (green) of a standard Cantor’s alloy after re-crystallization. Dynamic modulus normalized to its starting value at 300 K, that is E = (160±10) GPa. Room temperature frequency: 352 Hz.
Preprints 70530 g003
Preprints 70530 g004
Figure 4. Q-1 and Modulus of two Cantor’s alloy samples produced for SLM and cold worked. Second run. Black/gray data refers to the cold worked but not re-crystallized sample; magenta/red data to the cold worked and re-crystallized sample. Room temperature frequency: 589 Hz (not re-crystallized) and 860 Hz (re-crystallized). E = (90±10) GPa in the case of not re-crystallized sample to E = (170±10) GPa in the case of re-crystallized sample.
Figure 4. Q-1 and Modulus of two Cantor’s alloy samples produced for SLM and cold worked. Second run. Black/gray data refers to the cold worked but not re-crystallized sample; magenta/red data to the cold worked and re-crystallized sample. Room temperature frequency: 589 Hz (not re-crystallized) and 860 Hz (re-crystallized). E = (90±10) GPa in the case of not re-crystallized sample to E = (170±10) GPa in the case of re-crystallized sample.
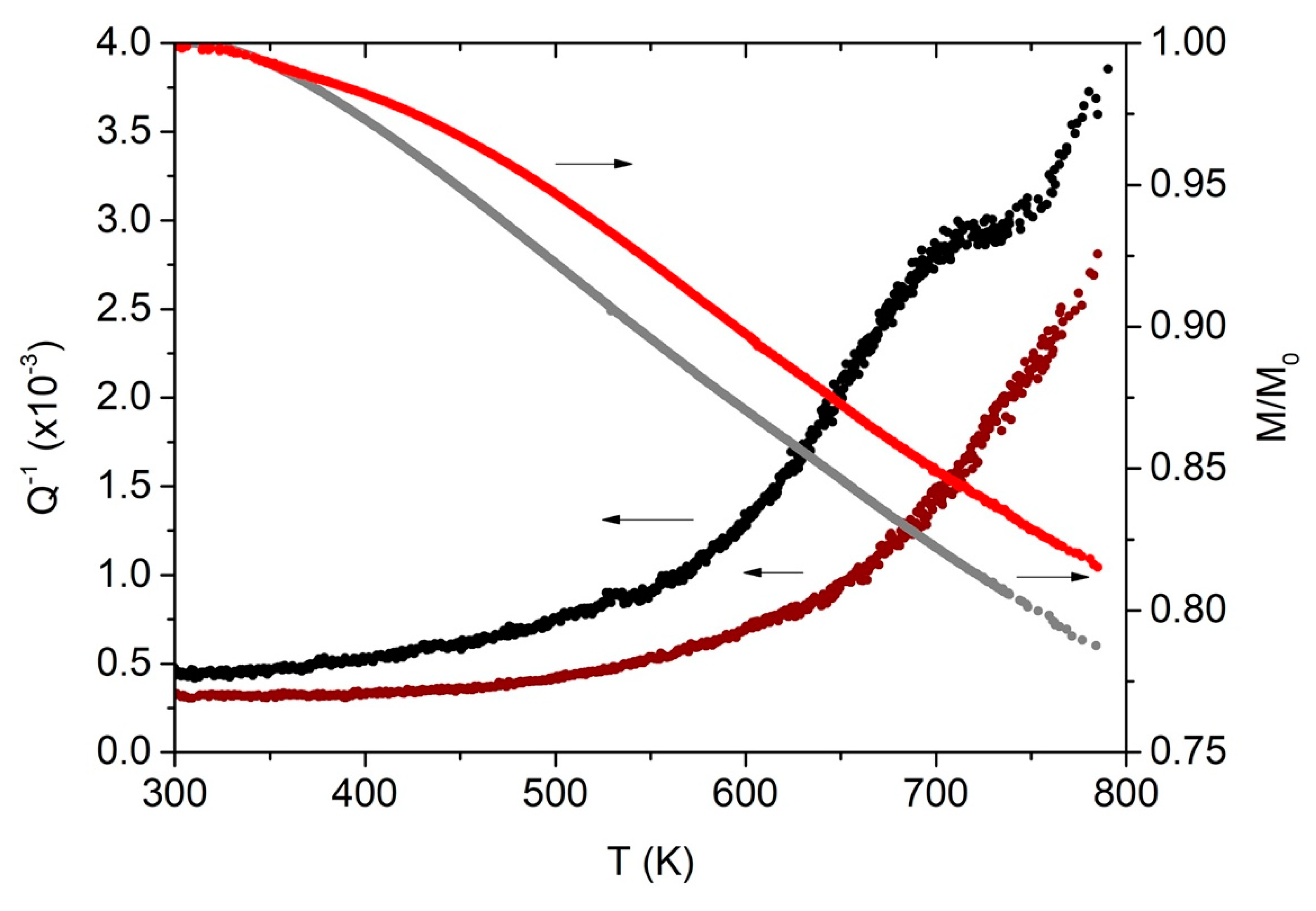
Preprints 70530 g004
Preprints 70530 g005
Figure 5. Q-1 of the sample of Figure 4 (black points), obtained by SLM and not re-crystallized, analyzed in terms of a growing background (olive) and a Debye (blue) peak. The red points are obtained adding the corresponding olive and blue points.
Figure 5. Q-1 of the sample of Figure 4 (black points), obtained by SLM and not re-crystallized, analyzed in terms of a growing background (olive) and a Debye (blue) peak. The red points are obtained adding the corresponding olive and blue points.
Preprints 70530 g005
Preprints 70530 g006
Figure 6. Diffraction pattern on an SLM sample after re-crystallization. Peaks are due to resin, FCC Cantor’s alloy (card number 00-033-0397), σ phase (card number 00-005-0708), Cr2N (card number Cantor’s alloy (card number 00-033-0397), σ phase (card number 00-005-0708), Cr N (card number 00-035-0803), CrN (card number 00-011-0065). 200-035-0803), CrN (card number 00-011-0065). Angol in radians. Reprinted from [22].
Figure 6. Diffraction pattern on an SLM sample after re-crystallization. Peaks are due to resin, FCC Cantor’s alloy (card number 00-033-0397), σ phase (card number 00-005-0708), Cr2N (card number Cantor’s alloy (card number 00-033-0397), σ phase (card number 00-005-0708), Cr N (card number 00-035-0803), CrN (card number 00-011-0065). 200-035-0803), CrN (card number 00-011-0065). Angol in radians. Reprinted from [22].
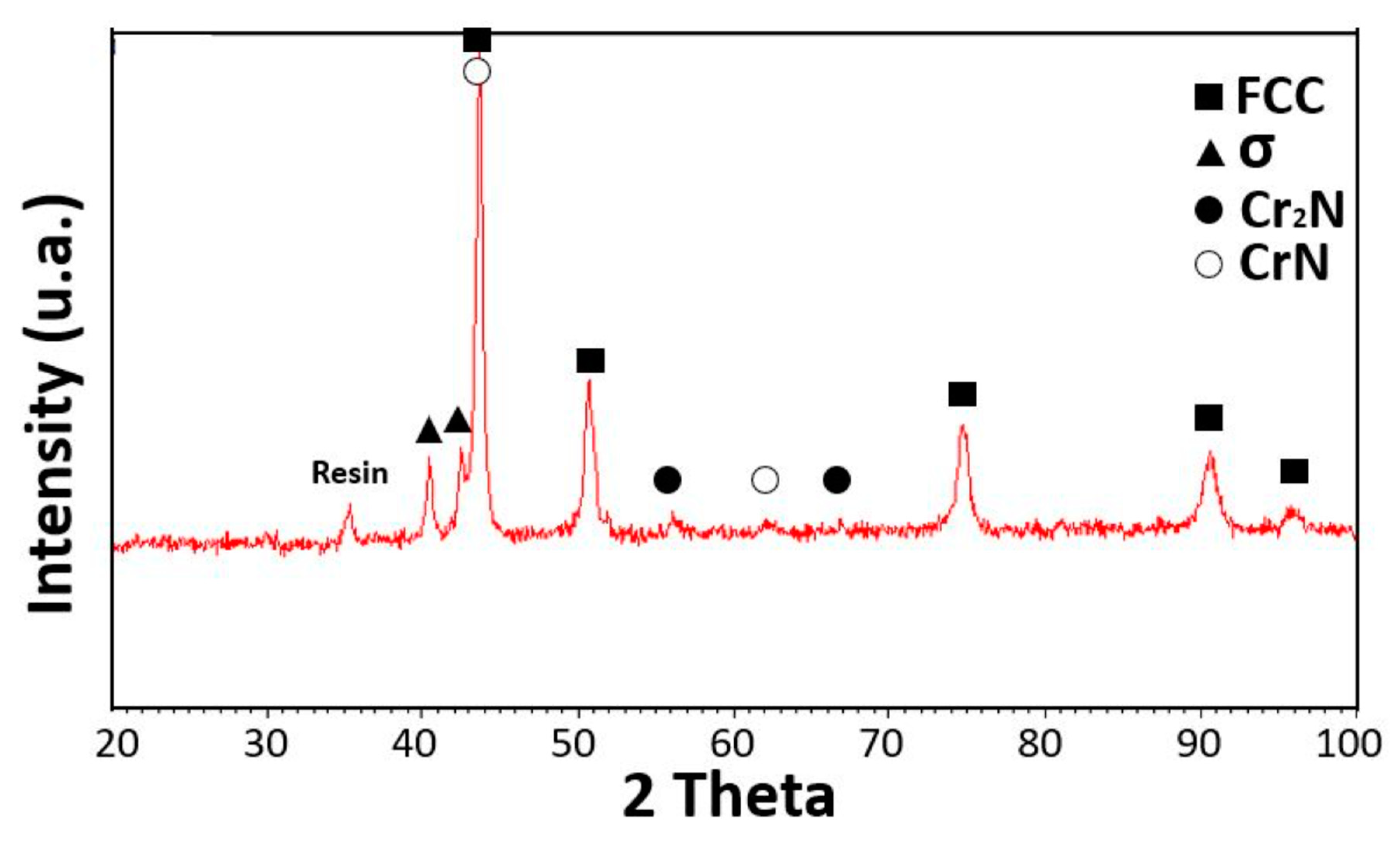
Preprints 70530 g006
Preprints 70530 g007
Figure 7. Standard sample microstructure images. (a) Cross-sectional image of a cold rolled sample. (b) Cross-sectional image of a cold-rolled sample after re-crystallization.
Figure 7. Standard sample microstructure images. (a) Cross-sectional image of a cold rolled sample. (b) Cross-sectional image of a cold-rolled sample after re-crystallization.
Preprints 70530 g007
Preprints 70530 g008
Figure 8. SLM sample microstructure images. (a) Cross-sectional image of a cold-rolled sample. (b) corresponding EBSD map, with FCC matrix in red and σ phase precipitates in blue. Precipitates are mainly at the grain boundaries, even if also found inside the grains. (c) SEM FEG high resolution precipitate image in an as-built sample. (d) Cross-sectional image of a sample cold-rolled and re-crystallized. Reprinted from [22].
Figure 8. SLM sample microstructure images. (a) Cross-sectional image of a cold-rolled sample. (b) corresponding EBSD map, with FCC matrix in red and σ phase precipitates in blue. Precipitates are mainly at the grain boundaries, even if also found inside the grains. (c) SEM FEG high resolution precipitate image in an as-built sample. (d) Cross-sectional image of a sample cold-rolled and re-crystallized. Reprinted from [22].
Preprints 70530 g008
Table 1. The parameter values obtained from fitting of the first run Q-1 data reported in Figure 2 (standard alloy) and of the second run of Figure 5 (SLM alloy).
Table 1. The parameter values obtained from fitting of the first run Q-1 data reported in Figure 2 (standard alloy) and of the second run of Figure 5 (SLM alloy).
Alloy H (eV) ∆ (10-4) Tp (K) A (10-4) B (10-6) C
standard 0.5 2.0 400 7 1.2 102
SLM 1.3 7.6 685 3.5 6.3 124
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Mechanical Spectroscopy Study of CrNiCoFeMn High Entropy Alloys

Enrico Gianfranco Campari

et al.

,

2023

Microstructural Study of CrNiCoFeMn High Entropy Alloy Obtained by Selective Laser Melting

Enrico Gianfranco Campari

et al.

,

2022

Effects of Heat Treatment on the Microstructure and Mechanical Properties of a Dual-Phase High-Entropy Alloy Fabricated via Selective Laser Melting

Xiaojun Tan

et al.

,

2024

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated