Preprint

Article

Noise Reduction in Helicopter Cabins Using Microperforated Panel Composite Sound Absorption Structures

Altmetrics

Downloads

153

Views

Comments

A peer-reviewed article of this preprint also exists.

Yang Lu^*,

Yang Lu^*,

This version is not peer-reviewed

Submitted:

21 June 2023

Posted:

21 June 2023

You are already at the latest version

Alerts

Abstract

The high level of noise in helicopter cabins considerably compromises the comfort and safety of the pilot and passengers. To verify the feasibility and effectiveness of microperforated panel composite sound absorption structures for noise suppression in helicopter cabins, simulation and experimental studies were conducted on a model of a light helicopter cabin. First, three microperforated composite sound absorption structures for the helicopter cabin wall panel were designed. Then, a finite element model of the main gear/body acoustic vibration coupling was established to obtain the target frequencies of the microperforated composite sound absorption structures; the acoustic effect was verified by simulation. Finally, a model helicopter cabin equipped with the three microperforated composite sound absorption structures was built, and a cabin noise test was performed. The test results showed that the combined microperforated panel acoustic structure and microperforated panel–porous material composite structure realized an overall cabin sound pressure level attenuation of 8–10 dB, on average, in the wide frequency range of 500–2000 Hz, with an amplitude of more than 20 dB. The microperforated panel–acoustic supermaterial composite structure achieved low-frequency sound absorption in the frequency range of 300–450 Hz. The sound absorption effect reached 50%, and it also exhibited good noise reduction effects in the middle- and high-frequency bands.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Helicopter cabin noise is very complex comprising noise generated from a variety of sources, including aerodynamic noise caused by the rotor system, transmission system, engine, and other components [1]. The main gearbox is a key component of the helicopter transmission system, and the impact excitation generated by the gear meshing causes structural vibration and induces cabin noise, whose frequency is usually in the range 200–2000 Hz. This noise has a high sound pressure level covering the sensitive range of human ear hearing, resulting in cabin noise levels exceeding 95 dB and even reaching 110 dB in many helicopter models [2]. Therefore, the noise generated by the main gear is one of the key factors limiting the development of new helicopters [3].

Figure 1 depicts the cabin noise spectrum of an S-76 helicopter cabin [4,5]. Clearly, the helicopter cabin noise is mostly medium–high frequency line spectrum noise with multiharmonic, multifrequency, and high-level characteristics. Currently, helicopter cabin noise control is mainly based on adding porous sound-absorbing materials, honeycomb structures, and damping materials to the cabin wall sandwich to reduce the sound energy propagation through vibration isolation and sound absorption techniques [6,7,8]. Two helicopter cabin wall panel structures are illustrated in Figure 2. As can be seen, the helicopter nacelles typically have a semi-thin-walled structure consisting of an external skin and longitudinal and transverse skeletons. Some civil helicopter models are equipped with interior panels, and their air-back cavities are often filled with sound-absorbing cotton and foam for acoustic treatment. This type of material has limited ability to control low- and medium-frequency noises and has a large additional mass, which affects the overall performance of the helicopter to some extent [5].

Sound absorption and isolation methods are easy to implement and the noise reduction effect is stable; hence, almost all helicopter manufacturers are currently using such methods. However, these methods have certain limitations including large additional weights and poor low-frequency effects. In recent years, a new type of acoustic structure, called microperforated panel (MPP) sound absorption structure, has been developed. It has the advantages of good sound absorption, simple structure, and low weight compared with traditional acoustic structures or materials [9,10]. The MPP structure has been widely used in the fields of building and road construction [11,12,13,14,15]; however, so far, its application in helicopters has been rarely studied. To reduce the linear spectrum noise in the helicopter cabin caused by gear meshing of the main gearbox, the original structure can be modified using the air-back cavity and converting the interior trim panel into an MPP. This strategy can not only reduce the noise but also meet the size and weight requirements of the helicopter. Models without interior panels can be retrofitted with MPPs to form a microperforated acoustic structure, which can effectively suppress cabin noise and satisfy the weight requirements.

According to the Helmholtz resonance principle, the sound absorption characteristics of a microperforated plate acoustic structure exhibit a single resonance peak. If used for noise reduction in helicopter cabins, the sound absorption band of the MPP structure needs to be broadened. The sound absorption band is mostly concentrated in the middle and high frequency; the low-frequency noise suppression effect of the structure is not good and cannot meet the requirement for noise reduction in helicopter cabins. Hence, this study proposes three composite MPP acoustic structures for noise reduction in helicopter cabins, namely, a combined MPP acoustic structure (hereinafter referred to as Combined MPP), MPP–porous material composite structure (hereinafter referred to as MPP+Porous), and MPP–acoustic supermaterial composite structure (hereinafter referred to as MPP+PAM), whose basic configurations are shown in Figure 3. Combined MPP consists of parallel MPPs with different properties, aiming to absorb the multilinear spectrum, high level noise, and broaden the absorption band. The MPP+Porous modifies the original interior panel for acoustic treatment by installing an MPP and filling the back cavity with porous acoustic materials to broaden the absorption band. The MPP+PAM combines an MPP and acoustic supermaterial of a thin plate type placed in the back cavity to suppress the noise in the middle- and low-frequency bands.

This study takes the helicopter cabin noise control as the research problem, focusing on the noise in the middle- and high-frequency bands of the multilinear spectrum caused by gear meshing of the main gear reducer, and investigates the feasibility and effectiveness of using MPP composite sound absorption structures for noise suppression in helicopter cabins. The remainder of this paper is organized as follows. Section 2 establishes the mathematical models of the absorption coefficient equations of the combined microperforated plate acoustic structures. Section 3 describes the simulation of the sound field in the model of a helicopter cabin equipped with microperforated plate composite acoustic structures. Section 4 presents the experiments on the sound field in the helicopter cabin model with the application of the microperforated plate composite acoustic structures. Finally, Section 5 concludes the paper.

2. Methodology

Figure 4 displays a schematic of the MPP acoustic structure for noise reduction in the helicopter cabin. The sound absorption structure mainly consists of a microperforated plate, an air-back cavity, and the external skin of the nacelle. Because the microperforated plate acoustic structure is not sensitive to material properties, to reduce the weight, a thin plate of polymer material with microperforations is used. The air-back cavity and rigid skin wall plate with a certain thickness left at the rear constitute the microperforated plate acoustic structure. The following concepts, based on the transfer matrix method combined with the series–parallel relationship, establish three MPP composite sound absorption structures for the sound absorption characteristic model.

2.1. Mathematical model of MPP

The transfer matrix of a microperforated plate [17,18] M is:

(1)

and its acoustic impedance rate can be expressed as:

(2)

The transfer matrix of the air back cavity C is given by

(3)

where D₁ is the depth of the air back chamber.

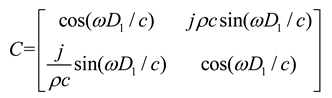
The transfer matrix of the MPP is as follows:

(4)

Because the terminal surface of the acoustic structure is a rigid wall plate, the acoustic impedance of the MPP can be obtained as:

(5)

The reflection coefficient R is as follows:

(6)

(7)

2.2. Mathematical model of MPP+Porous

Based on the sound absorption mechanism of porous sound-absorbing materials, the Johnson–Champoux–Allard model is chosen to describe the sound absorption coefficient of the material. The transfer matrix of a porous sound-absorbing material P is:

(8)

where k_p and Z_p are the wave number and characteristic impedance of the porous material, respectively, which are calculated as follows:

(9)

(10)

where ρ(ω) and K(ω) are the effective density and bulk modulus of the porous material, respectively, which are expressed as:

(11)

(12)

Here,

(13)

where α is the curvature factor, σ is the flow resistance, Φ is the porosity of the porous material, η is the dynamic viscosity of air, γ is the specific heat capacity ratio of air, P₀ is the static pressure of air, Pr is the Prandtl number of air, b is the cross-sectional shape factor of pores, b’ is the scale factor of pores, and Λ and Λ’ are the viscous and thermal characteristic lengths, respectively.

The porous material used in this study is melamine sponge, which is an open-cell porous foam acoustic material with excellent sound absorption performance and is widely used in aircraft adiabatic insulation, payload racks, and mufflers of the International Space Station. It has a good suppression effect on cabin noise, and its relevant parameters are listed in Table 1.

The transfer matrix of MPP+Porous is:

(14)

The absorption coefficient can be obtained by substituting the values into equations (5)–(7).

2.3. Mathematical model of MPP+PAM

The acoustic absorption mechanism of a thin-plate acoustic metamaterial is primarily based on the principle of local resonance to achieve the total absorption of a certain frequency of acoustic waves. In this study, the thin-plate acoustic metamaterial is composed of a rectangular aluminum thin plate and a small cylindrical iron block, whose individual metamaterial structure is depicted in Figure 5. The following derivation of the absorption coefficient of this composite structure is based on the modal superposition method.

The transfer matrix of the PAM is:

(15)

where Z_PAM is the impedance rate of the PAM.

A mass block of dimensional diameter R_mass is attached to the thin plate. In the Cartesian coordinate system, the coordinates of the center of the mass block circle are assumed to be (x0, y0), and the equation of the vibration motion of the thin plate with the mass block attached is:

(16)

where ρ_mass is the surface density of the mass block, p_in is the amplitude of the incident acoustic wave, H is the characteristic impedance of air, and ρ₀c₀ is the combination of four step functions characterizing the impact of the mass block equation, at the position of the mass block to take 1, the other positions of the thin plate to take 0, the expression is:

(17)

The vibration displacement of a thin plate can be expressed as:

(18)

where m is the modal number, Φ_m (x, y) is the modal type function of each order for a thin plate under fixed constraints, and q_m (t) is the generalized coordinate corresponding to the modal type function of each order. Here,

(19)

(20)

Substituting equation (20) into equation (18), multiplying by the orthogonal modal function Φ_n (x, y), and integrating over the surface of the thin plate, we obtain:

(21)

Equation (21) can be expressed as a matrix using the expression:

(22)

where [M_p] is the sheet mass matrix, [Q] is the additional mass matrix, [E] is the damping matrix with a damping factor of 0.15, [K] is the sheet stiffness matrix, [D] is the flexural stiffness matrix, and L is the nodal displacement.

The modal migration matrix [Y] can be expressed as:

(23)

The amplitude of the structural vibration velocity of the PAM at the vertical incidence of the acoustic wave is:

(24)

The average structural vibration velocity of the PAM is:

(25)

The impedance of the PAM is the ratio of the sound pressure difference between the two sides of the structure to the average vibration velocity of the structure, which can be expressed as:

(26)

The transfer matrix of MPP+PAM is:

(27)

The absorption coefficient can be obtained by substituting the values into equations (5)–(7).

3. Simulation

3.1. Simulation object

To conduct a simulation study of the sound field in the cabin of the model helicopter, the nacelle of the helicopter was selected as the simulation object. Figure 6 illustrates the nacelle structure of the model helicopter, whose fuselage length, width, and height are 2065, 580, and 564 mm, respectively. The model was designed based on a light helicopter shape and reducer arrangement. The fuselage structure was supported by the landing gear and fixed on the table structure. To reduce the processing difficulty, the nacelle was simplified into a polyhedral configuration, and the MPP was fixed on the helicopter nacelle wall plate, leaving an air-back cavity of appropriate thickness. Porous materials and acoustic supermaterials were introduced to form a composite acoustic structure. By designing reasonable structural parameters, the resonant frequency and sound absorption band of the composite MPP acoustic structure were adjusted to obtain a better noise-reduction effect.

3.2. Main reducer vibration source simulation

A dynamic model of the main gearbox was established to simulate more realistically the noise in the helicopter cabin caused by the main gearbox. Based on the physical parameters of the main gearbox in the cockpit of the model helicopter, the main gearbox dynamic model was constructed using finite element software, as shown in Figure 7. The length, width, and height of the main gearbox model were 250, 160, and 180 mm, respectively. The internal gearbox included two pairs of gears, with 60 and 32 teeth of the main wheel and 80 and 40 teeth of the driven wheel and a transmission ratio of 4/3.

In the multibody dynamic physical field, the transient response of the main reducer dynamic model was calculated, and a measurement point on the outer casing of the primary active wheel was selected to derive the average acceleration response curve in the frequency range 0–2000 Hz on the main reducer casing, as displayed in Figure 8. When the power input shaft speed was 900 rpm, the gear meshing frequencies and their harmonic frequencies generated by the main reducer in the frequency range 0–2000 Hz were mainly distributed at 360, 720, 900, 1080, 1440, and 1800 Hz. Based on the number of teeth and speed calculation, it was concluded that the internal gear meshing frequency of this main reducer was 360 Hz, which indicates that the main gear dynamic model can better simulate the vibration excitation environment of the main gear of the helicopter.

Furthermore, the main gear model was combined with the nacelle model through the spar. The dynamic response of the model nacelle was then simulated and calculated in the multibody dynamic physical field under the condition of the main gear vibration excitation, which was used for the subsequent acoustic field simulation calculation of the pressure acoustic physical field. The grid used in the model was a free tetrahedral grid cell. Because the maximum frequency of the analysis in this study is 2000 Hz, the grid cell size should be no larger than one-sixth of the wavelength. Therefore, the size of the grid cell was set to 28 mm, and fixed constraints were applied at the bottom of the landing gear. The main gear input shaft speed was set to 900 rpm, and the main gear output shaft torque was 6 N·m.

Figure 9. Finite element model of the helicopter.

3.3. Design parameters

The structural parameters of the three composite sound absorption structures were designed based on the obtained average acceleration spectrum of the main gearbox shell, as discussed in the previous section. Considering the small space inside the nacelle and convenience of subsequent processing, the thickness of the MPP was selected as 1 mm, and the depth of the air-back cavity was set as 20 mm. Therefore, Combined MPP only needs to consider the perforation rate and aperture of the two MPPs. The design resonant frequencies corresponded to 900 Hz and 1440 Hz, and the design sound absorption bandwidth was 500–2000 Hz. The design parameters of Combined MPP are listed in Table 2.

The porous acoustic material was melamine acoustic sponge, and its basic acoustic parameters are described in Section 2. Here, we only need the MPP parameters for the design. The design resonant frequency was 900 Hz, and the design acoustic bandwidth was 500–2000 Hz. The design parameters of MPP+Porous are listed in Table 3.

In MPP+PAM, the design of a single cell of a thin-plate acoustic metamaterial was first performed. As the boundary state of the thin-plate acoustic metamaterial affects the modal characteristics of the resonant system, a clamping device, consisting of two frames of the same size at the top and bottom, was used to fix it, as depicted in Figure 10.

The main parameters of MPP+PAM included the microperforated plate parameters, relevant parameters of the thin plate and mass block, and depth of the air-back cavity before and after the thin plate. The design resonance frequency was 360 Hz, and the design absorption bandwidth was 300–400 Hz. The design variables and ranges of the values for MPP+PAM are listed in Table 4.

Based on the three composite acoustic structure design parameters, the calculated absorption coefficient curves of the various composite acoustic structures in the frequency range of 0–2000 Hz were plotted, as shown in Figure 11.

As can be seen in Figure 11, the optimized structure exhibits good sound absorption at the designed resonant frequency and in the target frequency band. Under the condition of positive incidence of sound waves, the peak absorption is close to 1, which is equivalent to the performance of "perfect sound absorbers." Combined MPP and MPP+Porous have absorption coefficients greater than 0.5 in the 700–1400 Hz range. In contrast, MPP+PAM produces three absorption peaks through the mutual coupling of the microperforated plate and acoustic metamaterial owing to the introduction of new absorption peaks at low frequencies in the thin plate–mass block system. At the middle and high frequencies, the fourth-order modal resonance of the thin plate–mass block system coupled with the MPP forms a double absorption peak, but the absorption bandwidth becomes narrower. It can be observed that MPP+PAM achieves acoustic absorption at specific frequencies in the low-frequency band compared with the conventional resonant structure, while retaining the broadband absorption performance of the microperforated plate and thin plate vibration in the middle- and high-frequency bands.

3.4. Model cabin sound field simulation

In this study, three MPP acoustic structures for noise reduction in the cabin of a model helicopter were developed. For comparison and verification, cabin sound field simulations were carried out for two cabin wall panels with and without MPP acoustic structures to obtain the sound pressure level (SPL) distribution in the cabin and analyze the cabin noise reduction characteristics of MPP acoustic structures.

Based on the vibration response of the wall plate under real gear meshing conditions obtained from the vibration source simulation, the vibration acceleration responses of the back and bottom plates of the nacelle were used as the noise radiation source in the acoustic pressure field by a generalized stretching operator that mapped the values from the source end to the target end. Figure 12 illustrates the nacelle simulation model, where the helicopter nacelle consists of an external skin, an interior trim panel, and back and bottom plates as radiation sources. Four spherical domains within the model were used to simulate the human ear position of the occupants, and thus measure the noise signal at typical locations within the cabin. The noise reduction characteristics of the cabin equipped with the microperforated composite acoustic structure on the interior panel were analyzed by comparing the two cases with the original wall panel.

Through a pressure acoustic frequency domain simulation analysis, the SPL data of four typical measurement points in the cabin were acquired, and a weighted average was calculated to obtain the average SPL frequency response curve, as displayed in Figure 13.

As shown in Figure 13, the average SPLs of the four measurement points in the cabin after installing the composite microperforated plate acoustic structures are attenuated to different degrees in the target frequency band range. Among them, the average SPL in the cabin with Combined MPP (Figure 13a) is significantly attenuated in the frequency range of 500–1000 Hz and 1300–2000 Hz. The attenuation values are 10.9, 24.9, 7.2, and 10.4 dB at four engagement frequencies of 720, 900, 1080,and 1440 Hz, respectively. The average SPL in the cabin with MPP+Porous (Figure 13b) is substantially attenuated in the 500–1000 Hz and 1300–2000 Hz bands, with 15.3, 24.1, 6.4, and 11.9 dB attenuation at the four engagement frequencies of 720, 900, 1080, and 1440 Hz, respectively. The average SPL in the cabin with MPP+PAM (Figure 13c) is considerably attenuated in the frequency ranges of 350–500, 1300–1500, and 1700–2000 Hz, with 4.3, 23.4, and 11.3 dB attenuation at three engagement frequencies of 360, 900, and 1440 Hz, respectively. The three MPP composite sound absorption structures satisfactorily controlled the cabin noise in the target frequency range.

4. Experiment

To further verify the noise reduction effects of the microperforated plate acoustic structures on the helicopter nacelle, experimental studies were conducted in a model helicopter with a complete power unit, transmission system, and fuselage structure.

4.1. Test system

To facilitate the installation and removal of the MPP composite sound absorption structure, the simulated cabin was divided into six independent double-layer plate structures using fasteners to connect the plates. The interior trim plate was removable to facilitate the installation of the MPP. The back cavity behind the plate was used to fill the porous material and thin plate type acoustic supermaterial. The design diagram and physical drawing are displayed in Figure 15.

Based on this test system, the operating speed of the motor was set to 900 rpm, and the operating torque of the magnetic powder brake was 6 N·m. A single-axis acceleration sensor was mounted on the main gearbox housing to obtain the main gearbox vibration load spectrum, and four microphones were placed at typical cabin locations to measure the cabin noise level. Microphones 1 and 2 corresponded to the front and co-pilot positions, respectively, whereas microphones 3 and 4 corresponded to the occupant positions. The actual installation positions of each sensor are depicted in Figure 16. The three microperforated composite sound absorption structures and original wall panels were installed in the simulated cabin for testing, and the vibration levels of the main gear housing and sound field in the simulated cabin were measured.

The sound field test system in the cabin of the model helicopter is depicted in Figure 14, and the magnetic powder brake and other measurement and control hardware parameters are listed in Table 6. The test system scheme mainly consisted of the model helicopter, simulated cabin, and measurement and control subsystem. The MPP composite sound absorption structure was installed at the interior trim panel, replacing the original wall panel, and the vibration and noise levels were measured and analyzed before and after installation of the composite acoustic structure.

4.2. Vibration level test results

The measured acceleration spectrum in the 0–2000 Hz frequency band of the main reducer housing is shown in Figure 17. In the target frequency band of 500–2000 Hz, the gear meshing frequencies and their harmonic frequencies generated by the main reducer are mainly distributed at 360, 540, 720, 900, 1080, 1350, 1440, and 1800 Hz. In addition to the harmonic components in the design scheme, other frequency components, such as at 540 Hz and 1350 Hz, also exist; these are crossover and multiplication components owing to gear wear, clearance, and other nonlinear factors.

4.3. Cabin noisel test results

4.3.1. Time domain analysis

The measured sound pressure values of microphones 1–4 at typical positions in the 0–2000 Hz range in the cabin for 0–15 s for the three microperforated plate composite acoustic structures installed separately are displayed in Figure 18, Figure 19 and Figure 20. As shown, the sound pressure values at typical positions in the cabin for all three structures show significant attenuation, and the attenuation effects of microphones 1 and 2 are generally better than those of microphones 3 and 4, which may be due to the closer proximity of microphones 3 and 4 to the noise source.

To more intuitively reflect the attenuation effect, the sound pressure value was converted to SPL using the following equation:

(28)

where P_e and P₀ are the RMS and standard values of the sound pressure, respectively, and P₀=2×10^-5Pa.

In the range 0–2000 Hz, the SPL at the typical position in the cabin where Combined MPP was installed was attenuated by 2–4 dB. Considering the design frequency range of Combined MPP, the SPL at the typical position in the range 500–2000 Hz was obtained using band-pass filtering. In this frequency range, the SPL at each microphone position was attenuated by 9.2 dB on average, which is equivalent to a noise reduction effect of approximately 65%.

In the range 0–2000 Hz, the SPL at the cabin location where MPP+Porous was installed was attenuated by 2–3 dB. Considering the design frequency range of MPP+Porous, the sound pressure signal in the range 0–2000 Hz was band-pass filtered, and the SPL at the typical location in the range 500–2000 Hz was obtained. In this frequency range, the SPL at each microphone position was attenuated by 8.1 dB on average, equivalent to a noise reduction effect of approximately 61%.

In the range 0–2000 Hz, the SPL at the cabin location where MPP+PAM was installed was attenuated by 4.7 dB on average (a noise reduction effect of approximately 42%), because the noise at the engagement frequency of the low-frequency band was effectively controlled.

In summary, all microperforated plate composite acoustic structures exhibit satisfactory noise suppression effects in the target frequency range.

4.3.2. Frequency domain analysis

Fourier transformation of the sound pressure signal in the range of 500–2000 Hz was performed to obtain the SPL spectra at four typical locations in the cabin. To analyze the noise reduction effect in the cabin more intuitively, the SPLs measured at the four typical locations were averaged, and the overall SPL spectrum in the cabin was obtained, as shown in Figure 21, Figure 22 and Figure 23.

By observing the frequency response curve in each figure, the following can be observed:

Compared with the original wall panel, the three structures evidently attenuate the cabin SPL in the range of the resonance peak and its nearby frequency band, with a maximum attenuation greater than 20 dB.
Owing to the influence of the diffusion sound field, a new sound absorption band is formed, and the SPL with the three structures is attenuated by 10 dB, on average, over a wide frequency range of 1300–2000 Hz. The overall cabin noise level is effectively controlled.
MPP+PAM attains a significant cabin SPL attenuation in the range 300–450 Hz, with an average noise reduction effect of 45%. It also achieves a good low-frequency sound absorption effect and maintains satisfactory broadband noise reduction effects in the middle- and high-frequency bands.
Compared with the sound absorption performance of the ordinary MPP, those of the three structures are optimized to a certain extent. Combined MPP substantially improves the sound absorption performance in the 600–1100 Hz and 1400–1800 Hz ranges. MPP+Porous enhances the sound absorption performance in the range 600–1200 Hz. The reason for the weak optimization effect of the porous material here is that this material needs to be filled with a certain thickness to obtain the best sound absorption performance. After coupling with the MPP, the sound absorption performance is significantly optimized only near the resonance frequency. The sound absorption performance of MPP+PAM is considerably improved in the 300–450, 600–900, and 1600–1800 Hz ranges.

Combined MPP and MPP+Porous target the middle- and high-frequency band noise. Combined MPP is suitable for multiline spectrum middle- and high-frequency noise scenarios with restricted use space; however, the processing difficulty of multiple perforations is high. MPP+Porous is appropriate for single-line spectrum noise scenarios with larger use space. It has a simple process and lightweight material and can also be used with Combined MPP if the sound absorption band needs to be broadened. MPP+PAM is suitable for broadband noise scenarios; however, it is expensive and difficult to process, considering the extra weight of fixtures, preparation of thin plates and mass blocks, and other constraints.

In summary, the three proposed MPP composite sound absorption structures meet the design requirements and can effectively reduce the cabin noise level according to different target frequency bands with good broadband noise reduction characteristics.

5. Conclusion

Simulation and experimental studies of noise suppression in helicopter cabins based on composite acoustic structures of microperforated panels were conducted to verify their feasibility and effectiveness. The main conclusions are as follows:

The proposed MPP composite sound absorption structures can satisfactorily suppress the noise from the main gearbox in the target frequency band.
Based on the constructed finite element model of the helicopter main gear/body acoustic vibration coupling, the in-cabin noise reduction characteristics of the composite microperforated plate acoustic structures were obtained via simulation analysis. The simulation results show that Combined MPP and MPP+Porous significantly improve the acoustic bandwidth and acoustic performance and can effectively reduce the cabin noise level in the range 500–2000 Hz, with an attenuation amplitude of up to 35 dB. MPP+PAM achieves low-frequency noise control in the range 350–450 Hz and has a certain noise control effect in the middle- and high-frequency ranges.
Based on the constructed model helicopter test platform, the cabin sound field conditions of composite acoustic structures equipped with microperforated panels were tested under real main gear vibration excitation. The cabin sound fields were compared with that of the original wall panel to verify the cabin noise reduction characteristics of the composite MPP acoustic structures. The test results show that Combined MPP and MPP+Porous realize an overall cabin SPL attenuation of 8–10 dB, on average, in the wide frequency range of 500–2000 Hz, with an amplitude of more than 20 dB. MPP+PAM achieves low-frequency sound absorption in the frequency range of 300–450 Hz; the sound absorption effect reaches 45% and it also has good noise reduction effects in the middle- and high-frequency bands.

References

Yu H W, Sun D H, Li M Q, et al. Research on noise reduction technology in helicopter cabin[J]. Helicopter Technology, 2012(04):38-44.
Scheidler J, J. A review of noise and vibration control technologies for rotorcraft transmissions[C]//Proceedings of INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Hamburg, Germany: Institute of Noise Control Engineering, 2016, 253(5): 2986-2997.
Szefi J, T. Helicopter gearbox isolation using periodically layered fluidic isolators [D]. The Pennsylvania State University. 2003. [Google Scholar]
Lu Yang, Ma Xunjun, Wang Fengjiao. Research on active noise control technology in helicopter cabin[J]. Aviation manufacturing technology, 2016, 59(08):38-45.
Millott T A, Yoerkie C A, Welsh W A, et al. Flight test of active gear-mesh noise control on the S-76 aircraft[C]//Proceedings of the American Helicopter Society Washinton, USA: The American Helicopter Society Inc, 1998.
Caillet J, Marrot F, Unia Y, et al. Comprehensive approach for noise reduction in helicopter cabins[J]. Aerospace Science and Technology, 2012, 23(1): 17-25. [CrossRef]
Ang L Y L, Tran L Q N, Phillips S, et al. Low-frequency noise reduction by earmuffs with flax fibre-reinforced polypropylene ear cups[J]. Advances in Acoustics and Vibration, 2018, 1: 1-10.
Qin Datong. History and research progress of mechanical transmission science and technology[J]. Journal of Mechanical Engineering, 2003, 39(12) : 37-43.
He L, Zhu H-C, Qiu S-J, et al. Acoustic theory and engineering applications [M]. Beijing: Science Press, 2006.
Ao QB, Wang JZ, Li Y, et al. Research progress of low-frequency sound-absorbing materials[J]. Functional Materials,2020,51(12):12045-12050.
ZHA Xueqin. Transparent micro-perforated sound-absorbing material improves the sound quality of the newly built parliament hall[J]. Acoustic technology, 1994, 13(1):1-3.
MAO Dongxing, XIA Junfeng, HONG Zonghui. Study on sound barrier based on micro-perforated panel structure with top absorbing cylinder[J]. Acoustic technology, 1999(1):26-29.
Li, L.; Zhang, Z.; Huang, Q.; et al. A sandwich anechoic coating embedded with a micro-perforated panel in high-viscosity condition for underwater sound absorption[J]. Composite Structures, 2019, 235:111761. [CrossRef]
WU Qu, LIU Yan, Li Yaozu, et al. Simulation Study on Acoustic Performance of Ventilation Muffler of STC-GV Supercharger[J]. Machinery, 2021, 48(06):8-13+19.
Lee W, Y.; Kim J, C. ; Noh H M. Application of a micro-perforated panel absorber to reduce the curve squeal noise of railways[J]. Noise Control Engineering Journal, 2021, 69(06):507-517.
Chen Hongshang. Research on noise reduction method of micro-perforated web face gear transmission based on Helmholtz theory[D]. Nanjing University of Aeronautics and Astronautics,2015.
Ma, DY. Combined microperforated plate sound absorption structure[J]. Noise and Vibration Control, 1990(03):3-9.
Ma, DY. Theory and design of microperforated plate sound absorption structures[J]. Chinese Science,1975(01):38-50.

Figure 1. Noise spectrum of an S-76 helicopter cabin.

Figure 2. Helicopter cabin wall panel structure.

Figure 3. Schematic of the three MPP composite sound absorption structures.

Figure 4. Schematic of the MPP acoustic structure for helicopter cabin wall panels (the perforations are enlarged for illustration).

Figure 5. Schematic of the thin plate acoustic metamaterial.

Figure 6. Schematic of the model helicopter.

Figure 7. Main reducer dynamic model.

Figure 8. Average acceleration frequency response curve of the main reducer housing.

Figure 9. Finite element model of the helicopter.

Figure 10. Schematic of the PAM clamping device.

Figure 11. Sound absorption coefficient curves.

Figure 12. Cabin geometry model.

Figure 13. Average SPL frequency response curve in the cabin equipped with different MPP composite sound absorption structures (compared with the original wall plate).

Figure 14. Model helicopter test system.

Figure 15. Physical diagram of the simulated cabin and sample structure.

Figure 16. Measuring sensor mounting position.

Figure 17. Main reducer housing acceleration response spectrum.

Figure 18. Sound pressure values at typical locations in the cabin (Combined MPP).

Figure 19. Sound pressure values at typical locations in the cabin (MPP+Porous).

Figure 20. Sound pressure values at typical locations in the cabin (MPP+PAM).

Figure 21. Comparison of the overall noise in the cabin before and after installation of Combined MPP.

Figure 22. Comparison of the overall noise in the cabin before and after installation of MPP+Porous.

Figure 23. Comparison of the overall noise in the cabin before and after installation of MPP+PAM.

Table 1. Parameters of melamine sponge.

Parameters	σ(N·s·m-4)	∅	α_∞	Λ(μm)	Λ’(μm)
Numerical value	10500	0.995	1.0059	240	470

Table 2. Combined MPP design parameters.

Structure	Parameters	Numerical value	Parameters	Numerical value
Combined MPP	Pore size d₁	0.40 mm	Perforation rate p₁	2.88%
	Pore size d₂	0.57 mm	Perforation rate p₂	0.94%
	Plate thickness t	1.00 mm	Dorsal cavity depth D	20 mm

Table 3. MPP+Porous design parameters.

Structure	Parameters	Numerical value	Parameters	Numerical value
MPP+Porous	Pore size d	0.52 mm	Perforation rate p	1.11%
	Plate thickness t	1.00 mm	Dorsal cavity depth D	20 mm

Note: For the melamine sponge parameters, refer to Table 1.

Table 4. MPP+PAM design parameters.

Structure	Parameters	Numerical value	Parameters	Numerical value
MPP+PAM	Pore size d	0.53 mm	Perforation rate p	0.96%
	Depth of cavity in frontof thin plate D₁	10 mm	Depth of cavitybehind thin plate D₂	10 mm
	Thin plate thickness tp	0.2 mm	Thin plate length B	50 mm

Table 5. Test system equipment models and their parameters.

Equipment	Model
Magnetic powder brake	PB-B2-0.6
Acceleration sensor	LC0119
Microphone	378B11
Signal conditioner	CM3508
Data collector	NI USB6343

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.