Preprint
Article
A Computational Method for Complex-shaped Hydraulic Turbomachinery Flow Based on Immersed Boundary Method
Altmetrics
Downloads
101
Views
23
Comments
0
This version is not peer-reviewed
Submitted:
26 June 2023
Posted:
12 July 2023
You are already at the latest version
Alerts
Abstract
Traditional numerical techniques such as sliding mesh, dynamic grid mesh, and others, have many limitations in dealing with flow simulation with large-scale movement of solid boundaries; which is the case for complex-shaped hydraulic turbomachinery such as propellers, pumps and turbines. The immersed boundary (IB) method provides a new approach to solve the above limitations. Therefore, this study proposes an sharp-interface IB method based on the level-set function that is suitable for simulating the flow through turbomachinery with complex geometries. This method is applied to actual three-dimensional numerical simulations of high-Reynolds number propellers using an in-house computational fluid dynamics solver. The results show that the proposed method can provide comparatively accurate predictions of unsteady load coefficients within the propeller flow passage, and capture the correct propeller wake characteristics as well as the interaction between the propeller wake and free surface. This study aims at providing a theoretical basis and engineering reference for the application of the IB method in engineering numerical simulations.
Keywords:
Subject: Engineering - Marine Engineering
1. Introduction
In recent decades, computational fluid dynamics (CFD) has become one of the mainstream effective means by scholars to study the flow of hydraulic turbomachinery such as propellers, pumps and turbines in recent decades [1,2]. Compared to the experimental methods, CFD is comparatively cost-effective, requires shorter preparation periods, and can capture more flow details [3,4]. Nevertheless, there is still room for improvement in technology to simulate the flow field of turbomachinery with CFD [5].
Hydraulic turbomachinery realizes the transformation of energy by utilizing the rotation of the impeller. Therefore, in practical numerical simulations, interfaces provided by commercial software such as moving reference frame (MRF), sliding reference frame (SRF), sliding mesh (SM), and dynamic mesh (DM) are conventionally used to capture the dynamic rotation of the impeller [6]. Unfortunately, MRF and SRF methods cannot be used for unsteady-state numerical simulations [7,8], and steady-state simulations lose a lot of flow details in terms of time scale and often cannot meet researchers’ needs for in-depth studies of turbomachinery flows [9]. While the SM method can perform unsteady-state numerical simulations, it simplifies the rotation by separating the computational domain into rotating and stationary parts [10,11], which affects the accuracy of the flow solution at the interface between the rotational and stationary regions due to the interpolation operation involved. The DM based on the Arbitrary Lagrangian-Eulerian (ALE) method is a relatively accurate grid technique which can be realized by user-defined functions, but the large-scale boundary spacial movement during the rotation of turbomachinery poses a significant challenge to DM methods [12,13,14]. The excessive stretching or deformation of the grid during unsteady computations may lead to the occurrence of negative volume grids, which may cause the breakdown of computation. Furthermore, the cost of regenerating the grid is usually high, and the grid quality cannot be guaranteed, which adversely affects the overall accuracy and efficiency. In recent years, the overset grid has developed rapidly and has been applied in many turbomachinery studies due to its relatively strong robustness [15,16]. However, the required interpolation accuracy of physical quantity data exchange between the foreground and background grids is relatively high, and the search time for nested overlapping region units is long, which reduces the computational efficiency to some extent, and more importantly, orphan grids even appear in extreme cases. Notably, all of the above processing methods require the application of body-fitted meshes around the rotating machinery whereas turbomachinery usually has complex three-dimensional (3D) geometric structures, and it is quite challenging to generate sufficiently high-quality grids for complex regions. Over-complicated pre-processing process can also significantly reduce the efficiency of the entire numerical simulation process.
The emergence of the immersed boundary (IB) method provides an effective solution to the above drawbacks. It was first proposed by Peskin [17] in 1972 and was successfully applied to the study of the flow of red blood cells in heart valves. In the IB Method, the computational domain is discretized into a fixed Eulerian background grid and applied to the entire fluid and solid domains. Therefore, high-quality structured grids can be generated quickly within a few seconds, and there is no need to deal with grid stretching and transformation [18]. The effect of the solid on the flow field is solved by adding an equivalent volume force source term to the right-hand side (RHS) of the Navier-Stokes (N-S) equation to satisfy the solid boundary conditions. Currently, the feasibility of using the IB method to study turbomachinery has been validated in the research of some scholars. Posa, Balaras et al. have conducted a series of studies on different turbomachinery using a combination of the IB method and large eddy simulation (LES). Posa et al. [19] simulated the internal flow of a mixed-flow pump under off-design conditions, the simulation results showed good agreement with the experimental data. In addition, Balaras et al. [20] used the same method to study the wake of an submarine propeller, and the results demonstrated that the dynamic characteristics of the simulated tip vortex were corresponding to those shown in the experimental results. In further studies, Posa et al. [21]analyzed the turbulent flow characteristics of the wake field of a propeller at different advance coefficients, revealing the effects of the tip vortex and central vortex on the evolution of turbulence kinetic energy (TKE) in the wake flow. Moreover, Kang et al. [22] applied the curvilinear immersed boundary (CURVIB) method with LES to numerically simulate a full-scale marine hydrokinetic turbine (MHK), revealing for the first time the 3D downstream wake structure of the complete MHK turbine composed of three different regions. Similarly, Angelidis et al. [23] also used the CURVIB method to simulate the same type of MHK turbine. Liao et al. [24] tested the CURVIB method to capture the flow characteristics of a propeller working in crashback model under different grid resolutions, the results showed that different grid resolutions had similar predictions of the far-wake, but there were relatively large differences in predicting the length of the near-wake recirculation zone and vortex structure.
Although the IB method has been applied in few studies, it has not been widely used in practical engineering numerical simulations like most of the simulation method interfaces provided by commercial software. To some extent, this depends on the difficulty of capturing the three-dimensional geometry of complex objects using the IB method. Therefore, this paper introduces a the level-set (LS) based sharp-interface IB method which is suitable for simulating complex hydraulic turbomachinery flow [25,26]. Based on the in-house CFD code, the large eddy simulation (LES) of a three-blade propeller with complex shape is carried out by using the above method, and the unsteady load coefficient and wake characteristics are analyzed and evaluated, so as to verify the ability of this method to simulate the mechanical flow of complex hydraulic turbomachinery. In addition, this paper introduces a method to quickly establish a level set function field describing complex geometric boundaries based on two grids-interpolation-mapping, which can significantly reduce the LS function determination.
This paper is organized as follows: In Section 2, the basic numerical methods including the IB method adopted in our study are introduced. In Section 3, the computational scheme are presented. In Section 4, the simulation results and associated discussions are given. Finally, conclusions are listed in Section 5.
2. Computational Methodology
2.1. Governing Equations
The compressibility of fluids is generally neglected in the numerical simulation of hydraulic turbomachinery flow without phase change phenomenon such as cavitation [27,28]. Therefore, the continuity equation and Navier-Stokes (N-S) equation for incompressible fluids after being filtered by LES are as follows
Here, t is the physical time, and are the density and dynamic viscosity of the fluid respectively, p is the pressure, g is the gravity. and (for i=1, 2 and 3) represent velocity and grid coordinates in Cartesian coordinate system respectively, and their subscripts are defined according to Einstein summation convention. is the Kronecker delta tensor, denotes the external force introduced by the IB method, which only exists in the N-S equation at the IB nodes. The tilde represents the spatial implicit filter operator based on grid-scale in LES and is the anisotropic sub-grid scale (SGS) stress tensor generated by the above filtration. In this study, we apply the dynamic-Smagorinsky model by Lily [29] and Germano et al. [30] to conduct the parameterization of SGS tensor, based on the Boussinesq hypothesis [31], the SGS tensor is defined as
Here, is the strain-rate tensor, and is the eddy viscosity, as
where C is the dynamic model coefficient, is the filtering scale calculated by , in which V is the grid-cell volume.
2.2. Spatial discretization
The computational domain is discretized using a Marker and Cell (MAC) staggered grid based on the Cartesian coordinate system. The velocity field is established at the cell-face centers, while other physical quantities such as pressure, dynamic viscosity, and density are established at the cell centers. A sketch of an arbitrary grid cell is shown in Figure 1. All partial derivatives are solved by finite difference method, and the viscous term is solved by second-order central difference scheme. In order to adapt to the convection dominance condition of propeller rotating flow, cubic upwind interpolation (CUI) and linear interpolation are used to calculate the convection term. The CUI processes for an arbitrary physical quantity are are necessary to sample three stencil points, which are far upwind, upwind and downwind, and they are represented by subscript letters "u", "c" and "d" respectively [32], as
where can be calculated by
in which the is defined as .
2.3. Time discretization and advancement
In this paper, we employ the explicit scheme for time discretization and the second-order Runge-Kutta method (RK2) for time integration to advance the computational time. The projection method is used to solve the momentum equation at each time substep. Denote the RHS terms including advective term, viscous term, gravitational term, and SGS term for each stage of the RK2 as follows
where the superscript n is the index of sub-step in the RK2 for arbitrary time step N, taking values of 0, 1/2, 1, which respectively represent the state before time advancement and the 1st and 2nd sub-steps of time advancement. Thus the solution process of projection method can be summarized represented in the following equations:
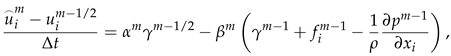
 Here, the definition of m is identical to the above-mentioned quantity n, whereas the value is . and denote the equation coefficients, when , the coefficients take on the values of 1 and 0, respectively. Conversely, when , both values of the coefficients are 1/2. is the velocity field after only considering the iteration of RHS terms, and is the velocity field that increases the existence of solids. Equation 10 is obtained by applying divergence-free conditions to both sides of the momentum equation, and the pressure Poisson equation on the RHS is solved by calling the interface provided by Portable, Extensible Toolkit for Scientific Computation (PETSc).
Here, the definition of m is identical to the above-mentioned quantity n, whereas the value is . and denote the equation coefficients, when , the coefficients take on the values of 1 and 0, respectively. Conversely, when , both values of the coefficients are 1/2. is the velocity field after only considering the iteration of RHS terms, and is the velocity field that increases the existence of solids. Equation 10 is obtained by applying divergence-free conditions to both sides of the momentum equation, and the pressure Poisson equation on the RHS is solved by calling the interface provided by Portable, Extensible Toolkit for Scientific Computation (PETSc).
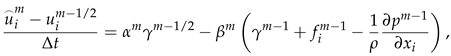

2.4. Complex body-identifying Method
2.4.1. Level-set based immersed boundary method
A sharp-interface IBM is employed for capturing the geometric bodies, the influence of bodies on flow field is realized by introducing source force into N-S equation. A signed LS function field is established within a Cartesian grid, where the LS function values indicate the distance from each grid node to the IB. The zero LS is defined as the IB, which represents the interface between the fluid and solid domain:
Figure 2 illustrates the IB method adopted in this paper, where the computational nodes can be classified as either fluid or solid based on the sign of the LS function, with positive values indicating fluid nodes and negative values indicating solid nodes, as
where represents the distance from node to the solid-fluid interface. A node is defined as an IB node if its LS function value is positive and at least one of its neighboring nodes is a solid node. For each IB node, its velocity is determined by interpolating the velocities of four stencil nodes to capture the effect of the solid on the flow field and satisfy the no-slip velocity boundary condition on the solid wall simultaneously. One of the stencil nodes is located on the IB and is a virtual node whose position is obtained by projecting the IB node along the gradient direction of the LS function, and its velocity is the local velocity of the solid. The remaining stencil nodes are fluid nodes adjacent to the IB nodes. Propellers and other hydraulic machinery have high flow Reynolds numbers, and their viscous sublayers cannot be fully resolved with a limited number of grids. Therefore, in this study, the simplified thin boundary layer equation (TBLE) is solved to interpolate the velocity at the IB nodes [33]:
where stands for the velocity in the tangential direction of the wall, represents the local friction velocity, is the von Kármán constant equals 0.41, is the damping coefficient which is specified as 17, y is the wall-normal coordinate, and is the wall-normal coordinate in wall units.
2.4.2. Interface tracking algorithm for establishing geometric level-set field
Establishing an accurate LS field is essential for the IBM based on LS functions used in this paper. For simple geometric bodies such as cylinders, spheres and airfoils, an analytical function can be provided to achieve this purpose. However, for highly complex moving objects in three-dimensional space, such as propellers, determining an analytical function is difficult. Thus, a fluid-bodies interface capturing method that is applicable to arbitrarily complex bodies is applied in this paper. Firstly, the commercial 3D modeling softwares are used to discretize the solid model into a surface mesh composed of numerous triangles. The information of the discretized geometry is stored in a standard triangle language (STL) file format, which includes the spatial coordinate vector information of each node in the triangle mesh. STL files are native to the stereolithography computer aided design (CAD) software created by 3D Systems and have been widely used for rapid prototyping, 3D printing and computer-aided manufacturing. The discretized geometry is shown in the Figure 3.
Notably, this triangular mesh only involves the establishment of LS function values, and does not participate in the flow computation. Each structured grid needs to traverse each discrete triangular face and obtain the minimum distance to the entire geometric surface mesh, which is the absolute value of the LS function, in order to obtain the minimum distance to any triangular surface of the structured grid. The sketch for solving the minimum distance from a structured grid to an arbitrary triangular surface is shown in Figure 4. In the sketch, , , and represent the coordinate vectors of the triangle vertices, and is the projection point of the structured grid onto the triangular plane along the normal direction of the triangle.
There are seven possible areas for the projection point on the plane, and the coefficients a, b, and c can be obtained by solving Eq. 16 to determine the area where the projection point is located. These coefficients satisfy the condition of .
The minimum distance is determined based on the location of the projection point. If the projection point is located inside the triangular surface (area (1)), the minimum distance is the distance from the grid node to the projection point. If it is located in areas (2)-(4), the minimum distance is the distance from the grid node to the triangle edge, while areas (5)-(7) correspond to distances from the grid node to the triangle vertex. The sign of the LS function in Eq. 13 is determined by applying the ray-casting method [34], that is, a ray from the structured mesh nodes pass through the triangular mesh simultaneously is randomly generated, as shown in Figure 5. If the number of times it passes through the triangular surface is even, the node is located outside the triangle, then it is assigned a positive sign; if the number of times it passes through the triangular surface is even, it is assigned a negative sign, corresponding to the node being outside the triangle.
2.4.3. Rapid updating method of level-set function
Due to the rotation of the propeller, the LS function used to describe the propeller geometry needs to be updated at each computational time step. For large-scale parallel computations, performing the traversal operation on the triangular surface mesh at every time step would be computationally expensive and significantly reduce the efficiency of the computation. Therefore, we introduce a two-mesh interpolation-mapping method to address this issue. Two sets of orthogonal Eulerian Cartesian meshes are adopted. Mesh 1 is used to identify the geometry of the propeller and establish the reference LS function field, Mesh 2 is for the numerical simulation, and the sketch is shown in Figure 6.
The domain of Mesh 1 is a box that is smaller than the computational domain but fully contains the propeller. The domain size is , discretized by points, resulting in a high resolution of approximately, this can obviously improve the accuracy of the definition of LS function. The geometric LS function values on Mesh 2 is obtained from a interpolation of the reference LS function values on Mesh 1 at the beginning of each time step. The interpolation process is described below. Firstly, the rotation of the propeller is treated as the reverse rotation of the grid coordinate system of Mesh 2 as
where is the angular velocity of propeller, and denote the coordinates before and after the rotational process in Mesh 2, respectively. The rotated coordinates of each grid node on Mesh 2 is used to search the corresponding closest cell center on Mesh 1 as the interpolation reference grid cell. The interpolation and mapping are carried out based on the LS function values at the reference and its adjacent cell centers. The interpolation is expressed as
where represents the LS value on Mesh 1, denotes the interpolated LS value on Mesh 2, subscripts , and represents the index of the reference cell on Mesh 1, and is the interpolation weight calculated as
where is the coordinates of the corresponding interpolation stencils on Mesh 1. After the above processing, the triangular surface mesh only need to be traversed once when the computation is initialized.
2.5. Front-capturing Method
For the case involving two-phase flow introduced in this paper, the method of coupled LS and volume-of-fluid (CLSVOF) is used to accurately capture the interface of air–water interface [35]. In our simulation, the density and dynamic viscosity of fluid are sharply defined based on the LS function, as
where is the LS function for describing the interface of two-phase fluid, denotes the viscosity or density of the fluid and the subscript letter “a” represents “air” and “w” represents “water”, respectively. H is a Heaviside function which is defined as
A piecewise linear calculation algorithm is employed in this study to reconstruct the interface, in which the normal direction of the interface and the distance from the interface to the cell center are determined by the LS function and the VOF function respectively. Interface reconstruction is carried out after the evolution of both LS and VOF at each time step, the evolution equation is as
where denotes the LS or VOF function.
3. Computational scheme
In this paper, a 3-blade DTMB P4119 propeller is selected as the research object, and the numerical simulation is carried out under the designed operating condition. The geometric characteristics and related parameters of the propeller model are shown in Figure 7 and Table 1 respectively, where the advance coefficient J is define by the free-stream velocity , rotation speed and diameter D, as
The geometric surface of the model propeller is discretized into 25,062 triangles with a total of 70,702 vertices. Time required to traverse all triangles in one time exceeds 100s. By applying the method mentioned in sub-subsection 2.4.3, the time cost by identifying the surface geometry at each time step reduces to less than 0.01s, which is negligible with respect to the time cost for solving the governing equations. Compared with conducting the traversal operation at each time step, it significantly saves the computational cost and improves the computational efficiency.
The computational domain of numerical simulation in this study is shown in Figure 8. The computational domain is a cuboid, and the length of the regions along the propeller axis, lateral direction and longitudinal direction is , and respectively. These three directions are discretized by grids of 920, 336 and 336, respectively. The mesh near the propeller is locally refined, and the highest local resolution reaches . Note that for the cases involving free surface, in order to ensure that the grid near the free surface has sufficient resolution, the grid in the longitudinal direction is increased to 384.
The axial boundary adopts periodic boundary conditions, and relaxation zones with lengths of and are applied on both sides of the axial inlet and outlet boundary respectively, to ensure stable inflow and outflow. The velocity field in the relaxation zone is determined by analysing Eqs. 24 and 25, as
where is the local dimensionless axial coordinates of relaxation zone, and the computed values and the target values are coupled in the relaxation zone according to the coupling coefficients at different locations. The boundaries in other directions are designated as free-slip walls.
In this paper, three different operating conditions for simulation and comparison is considered. One is the open-water condition that does not involve the free surface, and the other two are the two-phase flow issues of propeller operates beneath the flat inflow and incident third-order Stokes waves. The entrance height of the free surface is designated as 2.5D, which means that the submerged depth of the propeller is 0.75D. The wavelength and steepness of the third-order Stokes wave are and , respectively. All computations are performed on high-performance computing platform. A total of 576 CPUs are used and parallelization is performed by MPI (Massage Passing Interface) for solving the flow field.
4. Results and discussion
4.1. Unsteady loads
To verify the accuracy of the computation results and the influence of free surface and incident waves on the propeller, we evaluated the unsteady load coefficients and efficiency under various operating conditions and compared them with the experimental values. See Eqs. 26 for the definitions of thrust coefficient , torque coefficient and propeller efficiency .
where T represents the thrust and Q represents the torque. The unsteady load coefficients of numerical simulation is obtained by averaging 12 rotation periods after the flow enters a relatively stable stage, and the comparison results are shown in the Table 2.
The numerical simulation results show good agreement with the experimental data for the unsteady load coefficients, with errors for all operating conditions being positive and less than 5%. However, due to the bias of the errors towards one direction, the calculated efficiency is closer to the experimental value and less than 1%. The mean thrust and torque coefficients for the flat inflow and incident wave conditions are equal after approximations, and both are smaller than those for the open-water condition.
Figure 10 presents the time series of thrust and torque coefficients in a single propeller rotation period. The plot shows that for the two conditions involving a free surface, the trend of the unsteady load coefficients variation are consistent with that of the open-water condition. Although the mean coefficient values are the same of these two conditions, the curves in a single rotation do not demonstrate overlap completely, where the fluctuation amplitude of the thrust and torque coefficients under the incident waves condition is relatively higher than that under the flat inflow condition.
4.2. Wake properties of open-water condition
In this section, the captured properties of wake flow under open-water condition are analyzed, and the flow field of 36 phases in 12 rotation periods under open-water condition is averaged, and the phase-averaged flow field are obtained, as shown in the Figure 11.
Due to the rotational motion of the propeller, the incoming flow gains momentum and accelerates after passing through the propeller-disk at , forming a high-velocity slipstream region in the wake. There is a relatively low-velocity region downstream of the propeller center, which is mainly due to the blocking effect of the hub on the flow and the rotation-induced hub separation flow. In addition, there is also a low-velocity region outside the slipstream region due to the separation flow from the tip of the propeller blades. To satisfy the conservation of momentum, the slipstream region need to experience contraction downstream of the propeller due to the increase in fluid velocity, i.e. the area of the slipstream region decrease in the radial direction. The simulation results show the clearly slipstream contraction phenomenon in the wake, within a certain distance downstream of the propeller, the radius of the high-velocity slipstream region decreases as a whole, for instance as the presented slice at the section of . At the further sections downstream the propeller, due to the stability of wake decreases and dissipation of energy, the velocity of the slipstream region decreases and occupying a larger section area.
To further verify the correctness and rationality of the numerical simulation results, we selected several representative circumferential sections at different radii from blade tip to blade root, including , , and , for discussion. The Figure 12 illustrates the axial velocity and pressure distribution of the above section.
The velocity and pressure distributions of each section exhibit the correct flow characteristics, showing that the leading edge of the propeller blades collide with the incoming flow, producing a high-pressure region and causing a decrease in velocity near the leading edge. The fluid between the blades is accelerated to form a high-velocity region. The pressure distribution of the airfoil shows that the suction surface is significantly lower than the pressure surface, and the propeller generates a thrust in the opposite direction to the incoming flow due to the pressure difference. Within a range downstream of the propeller in each section, both the velocity and pressure exhibit quasi-periodic distribution characteristics, with high and low velocity and pressure regions alternating, representing the cross-sections of the vortices shed from the propeller blades. This periodic distribution persists for a longer length near the root of the blade. However, as we move outward along the radial direction of the propeller, the periodic distribution begins to disappear, and the vortices shed from different blades mix with each other. This phenomenon occurs earlier as we move closer to the tip of the blade, indicating that the shedding of vortices from the outer region of the propeller is more prone to instability.
4.3. Influence of propeller rotation on free surface
Under the design advance coefficient , the influence of the free surface on the qualitative distribution characteristics of the propeller wake is relatively small, and the macroscopic wake is consistent with that of the open water condition. We have discussed this aspect in more specific in other studies, and more details can be found in the Reference [37]. Therefore, we will not repeat the discussion of velocity and pressure characteristics under flat inflow and wave conditions. This section mainly discusses the effect of propeller rotation and wake on the variation of free surface elevation to emphasize the accuracy of the two-phase interface capturing method used in this paper. The transient free surface shape and relative height distribution under the above two conditions are shown in Figure 13. Under both conditions, the propeller did not show a significant influence on the elevation of the upstream free surface, but the effect was reflected at the center of the propeller and further downstream. The distribution of the wake free surface elevation was the same under both conditions. The motion of the propeller led to a decrease in the elevation of the propeller free surface, primarily at the downstream centerline of the propeller. As the flow developed downstream, the downward effect of the free surface would spread laterally, and the elevation of the free surface downstream of the centerline of the propeller would rise again, which is consisted with the phenomenon observed in the study by Lungu [38] and Di Mascio et al. [39]. The shape of the free surface would undergo periodic fluctuations due to the rotation of the propeller, which was more pronounced under the flat inflow condition. Under the incident wave condition, the periodic fluctuations of the wave surface would weaken the observation of the fluctuations caused by the rotation of the propeller to some extent.
5. Conclusions
This study employed the LES turbulence modeling technique and the IBM based on the LS function to numerically simulate the complex flow field of the DTMB P4119 at a high-Reynolds number with a design advance coefficient of . Unsteady load coefficients, wake flow properties, and the influence of the wake on the free surface were computed and discussed. The main conclusions are as follows:
(1)The interpolation-mapping method between two meshes used in this paper only requires traversing the three-dimensional geometric surface mesh once during the initialization of computation. This reduces the time required to establish the LS function field in each time step to less than 0.1s, provided that the LS function is accurately defined. As a result, the time required for establishing the LS function field is negligible compared to the time required for solving the momentum equation.
(2) The unsteady-state load coefficient, thrust coefficient, and torque coefficient under different operating conditions agree well with the experimental values, and the error in each condition is within 5%. In addition, for the two operating conditions involving a free surface, the unsteady-state behavior of the load coefficients under the incoming wave condition is relatively flat compared to that under the inflow condition.
(3) The analysis of the wake characteristics under the open water condition shows that the accuracy of the numerical method used in this study in capturing the flow characteristics of the propeller wake. The quasi-periodic nature of the intermediate velocity pressure in the near-wake, and the slip contraction phenomenon are correctly captured. In addition, it was found that the flow at the root of the blade dissipates later than that near the blade tip, and the quasi-periodic duration is longer.
(4) The disturbance caused by the operation of the propeller on free surface captured by CLSVOF method is consistent with the phenomenon reported by previous scholars. Under both the flat inflow condition and the incident waves condition, similar disturbance characteristics are exhibited, the elevation of the free surface downstream of the propeller first decreases and then increases along the central axis, and the decrease of the elevation will spread laterally.
Author Contributions
Conceptualization, K.K.; methodology, H.L. and K.K. ; software, H.L. and K.K.; validation, H.L. and K.K.; formal analysis, H.L. and K.K.; investigation, H.L. and K.K.; resources, K.K. and H.C.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, K.K., H.C. and M.B.; visualization, H.L.; supervision, K.K., J.F., Y.Z. and H.X.; project administration, J.F., Y.Z. and H.X.; funding acquisition, K.K and H.L.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangsu Province (BK20200509), the Postdoctoral Research Foundation of China (2022T150185; 2022M711021), and the Project on Excellent Post-graduate Dissertation of Hohai University (422003515).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature and Abbreviations
Nomenclature
| , , | Orthogonal coordinate direction |
| i, j, k | Indices representing x, y and z directions |
| u | Velocity |
| p | Pressure |
| t | Physical time |
| Density | |
| Dynamic viscosity | |
| Kronecker delta tensor | |
| External force introduced by the IB method | |
| SGS stress tensor | |
| Eddy viscosity | |
| Strain-rate tensor | |
| C | Dynamic model coefficient of LES |
| filtering scale of LES | |
| V | Grid-cell volume |
| Arbitrary physical quantity | |
| RHS term of N-S equation | |
| , | Coefficients of RK2 |
| m, n | Indices of sub-step in the RK2 |
| LS function used to describe body–fluid interface | |
| Velocity in the tangential direction of the wall | |
| local friction velocity | |
| Von Kármán constant | |
| damping coefficient | |
| wall-normal coordinate in wall units | |
| , | Coordinates before and after the rotational process in Mesh 2 |
| Coordinates of the corresponding interpolation stencils | |
| Interpolation weight function | |
| LS function used to describe air–water interface | |
| Viscosity or density of the fluid | |
| H | Heaviside function |
| LS or VOF function | |
| J | Advance coefficient |
| Rotation angular velocity | |
| Free-stream velocity | |
| D | Diameter |
| Rotation speed | |
| Rotation period | |
| T, Q | Thrust and torque |
| , | Thrust coefficient and torque coefficient |
| Efficiency | |
| h | Free surface elevation |
Abbreviations
| CFD | Computational fluid dynamics |
| MRF | Moving reference frame |
| SRF | Sliding reference frame |
| SM | Sliding mesh |
| DM | Dynamic mesh |
| ALE | Arbitrary-Lagrange-Eulerian |
| 3D | Three dimensional |
| N-S | Navier-Stokes |
| RHS | Right-hand side |
| LES | Large-eddy simulation |
| IB | Immersed boundary |
| TKE | Turbulence kinetic energy |
| MHK | Marine hydrokinetic turbine |
| CURVIB | Curvilinear immersed boundary |
| SGS | Sub-grid scale |
| MAC | Marker and Cell |
| CUI | Cubic upwind interpolation |
| RK2 | Runge-Kutta method |
| MPI | Message passing interface |
| PETSc | Portable, Extensible Toolkit for Scientific Computation |
| LS | Level-set |
| STL | Standard triangle language |
| CAD | Computer aided design |
| VOF | Volume-of-fluid |
| CLSVOF | coupled level-set and volume-of-fluid |
| DTMB | David Taylor model basin |
References
- Pinto, R.N.; Afzal, A.; D’Souza, L.V.; Ansari, Z.; Mohammed Samee, A. Computational fluid dynamics in turbomachinery: a review of state of the art. Archives of Computational Methods in Engineering 2017, 24, 467–479. [Google Scholar] [CrossRef]
- Tiwari, G.; Kumar, J.; Prasad, V.; Patel, V.K. Utility of CFD in the design and performance analysis of hydraulic turbines—A review. Energy Reports 2020, 6, 2410–2429. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Xu, Z.; Zheng, Y.; Gao, Q.; Shen, L. Energy loss mechanism due to tip leakage flow of axial flow pump as turbine under various operating conditions. Energy 2022, 255, 124532. [Google Scholar] [CrossRef]
- Chen, G.; Gu, C.; Hajaiej, H.; Morris, P.J.; Paterson, E.G.; Sergeev, A. OpenFOAM computation of interacting wind turbine flows and control (I): free rotating case. International Journal of Hydromechatronics 2021, 4, 1–26. [Google Scholar] [CrossRef]
- Nautiyal, H.; Kumar, A.; others. Reverse running pumps analytical, experimental and computational study: A review. Renewable and Sustainable Energy Reviews 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- McNaughton, J.; Afgan, I.; Apsley, D.; Rolfo, S.; Stallard, T.; Stansby, P. A simple sliding-mesh interface procedure and its application to the CFD simulation of a tidal-stream turbine. International journal for numerical methods in fluids 2014, 74, 250–269. [Google Scholar] [CrossRef]
- Yin, J.; Wang, D.; Walters, D.K.; Wei, X. Investigation of the unstable flow phenomenon in a pump turbine. Science China Physics, Mechanics & Astronomy 2014, 57, 1119–1127. [Google Scholar]
- Liu, J.; Lin, H.; Purimitla, S.R. Wake field studies of tidal current turbines with different numerical methods. Ocean engineering 2016, 117, 383–397. [Google Scholar] [CrossRef]
- Kan, K.; Xu, Z.; Chen, H.; Xu, H.; Zheng, Y.; Zhou, D.; Muhirwa, A.; Maxime, B. Energy loss mechanisms of transition from pump mode to turbine mode of an axial-flow pump under bidirectional conditions. Energy 2022, 257, 124630. [Google Scholar] [CrossRef]
- Nouroozi, H.; Zeraatgar, H. A reliable simulation for hydrodynamic performance prediction of surface-piercing propellers using URANS method. Applied Ocean Research 2019, 92, 101939. [Google Scholar] [CrossRef]
- Ahmed, S.; Croaker, P.; Doolan, C.J. On the instability mechanisms of ship propeller wakes. Ocean Engineering 2020, 213, 107609. [Google Scholar] [CrossRef]
- Wu, F.L.; Peng, Y.L.; Zhang, Z.G.; Wang, G.D. Application of dynamic mesh in analysis of propeller hydrodynamic characteristics. Applied mechanics and materials. Trans Tech Publ 2012, 212, 1112–1118. [Google Scholar] [CrossRef]
- Zhong, J.; Xie, Z.; Wang, C.; Shen, D.; Wang, H. A fast mesh deformation method for marine propeller flow. International Journal of Computational Fluid Dynamics 2018, 32, 444–453. [Google Scholar] [CrossRef]
- Huang, S.; Guo, J.; Yang, F. Numerical simulation of 3D unsteady flow in a rotating pump by dynamic mesh technique. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2013, Vol. 52, p. 022030.
- Shen, Z.; Wan, D.; Carrica, P.M. Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering. Ocean Engineering 2015, 108, 287–306. [Google Scholar] [CrossRef]
- Wang, L.; Wu, T.; Gong, J.; Yang, Y. Numerical simulation of the wake instabilities of a propeller. Physics of Fluids 2021, 33, 125125. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: a numerical method. Journal of computational physics 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Sotiropoulos, F.; Yang, X. Immersed boundary methods for simulating fluid–structure interaction. Progress in Aerospace Sciences 2014, 65, 1–21. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A.; Balaras, E. Large-eddy simulation of a mixed-flow pump at off-design conditions. Journal of Fluids Engineering 2015, 137. [Google Scholar] [CrossRef]
- Balaras, E.; Schroeder, S.; Posa, A. Large-eddy simulations of submarine propellers. Journal of Ship Research 2015, 59, 227–237. [Google Scholar] [CrossRef]
- Posa, A.; Broglia, R.; Felli, M.; Falchi, M.; Balaras, E. Characterization of the wake of a submarine propeller via large-eddy simulation. Computers & fluids 2019, 184, 138–152. [Google Scholar]
- Kang, S.; Borazjani, I.; Colby, J.A.; Sotiropoulos, F. Numerical simulation of 3D flow past a real-life marine hydrokinetic turbine. Advances in water resources 2012, 39, 33–43. [Google Scholar] [CrossRef]
- Angelidis, D.; Chawdhary, S.; Sotiropoulos, F. Unstructured Cartesian refinement with sharp interface immersed boundary method for 3D unsteady incompressible flows. Journal of Computational Physics 2016, 325, 272–300. [Google Scholar] [CrossRef]
- Liao, F.; Yang, X.; Wang, S.; He, G. Grid-dependence study for simulating propeller crashback using large-eddy simulation with immersed boundary method. Ocean Engineering 2020, 218, 108211. [Google Scholar] [CrossRef]
- Cui, Z.; Yang, Z.; Jiang, H.Z.; Huang, W.X.; Shen, L. A sharp-interface immersed boundary method for simulating incompressible flows with arbitrarily deforming smooth boundaries. International Journal of Computational Methods 2018, 15, 1750080. [Google Scholar] [CrossRef]
- Kan, K.; Yang, Z.; Lyu, P.; Zheng, Y.; Shen, L. Numerical study of turbulent flow past a rotating axial-flow pump based on a level-set immersed boundary method. Renewable Energy 2021, 168, 960–971. [Google Scholar] [CrossRef]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renewable Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Kan, K.; Binama, M.; Chen, H.; Zheng, Y.; Zhou, D.; Su, W.; Muhirwa, A. Pump as turbine cavitation performance for both conventional and reverse operating modes: A review. Renewable and Sustainable Energy Reviews 2022, 168, 112786. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Physics of Fluids A: Fluid Dynamics 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Physics of Fluids A: Fluid Dynamics 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent flows; Cambridge university press, 2000.
- Yang, Z.; Lu, M.; Wang, S. A robust solver for incompressible high-Reynolds-number two-fluid flows with high density contrast. Journal of Computational Physics 2021, 441, 110474. [Google Scholar] [CrossRef]
- Wang, M.; Moin, P. Dynamic wall modeling for large-eddy simulation of complex turbulent flows. Physics of Fluids 2002, 14, 2043–2051. [Google Scholar] [CrossRef]
- Gilmanov, A.; Sotiropoulos, F.; Balaras, E. A general reconstruction algorithm for simulating flows with complex 3D immersed boundaries on Cartesian grids. Journal of Computational Physics 2003, 191, 660–669. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. Journal of computational physics 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Jessup, S.D. An experimental investigation of viscous aspects of propeller blade flow; The Catholic University of America, 1989.
- Kan, K.; Li, H.; Yang, Z. Large eddy simulation of turbulent wake flow around a marine propeller under the influence of incident waves. Physics of Fluids 2023, 35, 055124. [Google Scholar]
- Lungu, A. Overall performances of a propeller operating near the free surface. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2020, Vol. 916, p. 012054.
- Di Mascio, A.; Dubbioso, G.; Muscari, R. Vortex structures in the wake of a marine propeller operating close to a free surface. Journal of Fluid Mechanics 2022, 949, A33. [Google Scholar] [CrossRef]
Figure 1.
Sketch of the arrangement of physical quantities in staggered grids.

Figure 2.
Sketch of immersed boundary method.

Figure 3.
Discrete unstructured mesh of a propeller in STL format.

Figure 4.
Sketch of (a)triangular surface and (b) distance calculation method.

Figure 5.
Schematic diagram of ray-casting method.

Figure 6.
Schematic diagram of interpolation-mapping process of level-set function from Mesh 1 to Mesh 2.
Figure 6.
Schematic diagram of interpolation-mapping process of level-set function from Mesh 1 to Mesh 2.

Figure 7.
Sketch of the model propeller.

Figure 8.
Sketch of computational domain and boundary conditions.

Figure 9.
Sketch of operating conditions for (a)open-water, (b) flat inflow and (c) incident waves.

Figure 10.
Time series of (a) thrust coefficients and (b) torque coefficients in a single rotation period
Figure 10.
Time series of (a) thrust coefficients and (b) torque coefficients in a single rotation period

Figure 11.
Distribution of phase-averaged axial velocity

Figure 12.
Circumferential sections at different radii of r/R = 0.95, 0.70, 0.40 and 0.2 contoured by phase-averaged (a) axial velocity and (b) pressure.
Figure 12.
Circumferential sections at different radii of r/R = 0.95, 0.70, 0.40 and 0.2 contoured by phase-averaged (a) axial velocity and (b) pressure.

Figure 13.
Iso-surface of free surface contoured by the elevation.

Table 1.
Parameters of DTMB P4119 propeller model
| Free-stream velocity () | Diameter (D) | Rotation speed () | Advance coefficient (J) |
|---|---|---|---|
| 2.541 m/s | 305mm | 600 rps | 0.833 |
Table 2.
Comparison of unsteady load coefficients between simulation and experimental values
| Condition | Error (%) | 10 | Error (%) | (%) | Error (%) | |
| Experiment [36] | 0.1460 | - | 0.2800 | - | 69.14 | - |
| Open-water | 0.1530 | +4.79 | 0.2919 | +4.25 | 69.49 | +0.51 |
| Flat inflow | 0.1501 | +2.81 | 0.2906 | +3.79 | 68.48 | -0.95 |
| Incident waves | 0.1501 | +2.81 | 0.2906 | +3.79 | 68.48 | -0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
A Computational Method for Complex-shaped Hydraulic Turbomachinery Flow Based on Immersed Boundary Method
Haoyu Li
et al.
,
2023
The One-way FSI Method Based on RANS-FEM for the Open Water Test of a Marine Propeller at the Different Advance Coefficient
Mobin Masoomi
et al.
,
2021
Validation of HiG-Flow Software for Simulating Two-Phase Flows with a 3D Geometric Volume of Fluid Algorithm
Aquisson T. G. da Silva
et al.
,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated












