Preprint
Article
Maximal Bell Violations with Predetermined Observables
Altmetrics
Downloads
263
Views
158
Comments
1
This version is not peer-reviewed
Submitted:
11 October 2023
Posted:
13 October 2023
Read the latest preprint version here
Alerts
Abstract
Alice and Bob make independent measurements for non-identical properties. If every Alice (or Bob) event is fixed for any choice of measurement by Bob (or Alice), can they violate a Bell-type inequality? In theory, the answer is negative if all the properties are measured at the same time. However, the answer is positive if only one pair of events is recorded in each iteration. This fact is not widely acknowledged, though often discussed at specialized conferences, because it does not seem to make sense. The overlooked nuance is that staggered events allow for pairwise combinations that are not possible for simultaneous coincidences. This can be illustrated with two synchronized “wheel-of-fortune” tables, while focusing on the patterns of coincidence between consecutive (rather than simultaneous) events.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
Quantum entanglement is able to violate the Bell inequalities, but only in special conditions. First of all, selected observables cannot exist at the same time, as part of a single system. This is why Bell experiments are conducted with non-commuting variables [1,2]. Secondly, predictions only hold for joint measurements with two events. If three observables or more are considered at the same time, then Bell violations are impossible. This is known as “quantum monogamy” [3]. From a mathematical point of view, these limitations are in perfect agreement with Bell’s Theorem, because the latter only holds for jointly distributed variables [4,5]. In other words, it works exclusively for properties that are real at the same time (and therefore it does not matter if two observables are measured at a time, or all of them). More importantly, this means that Bell’s inequality does not apply to mutually exclusive properties. Hence, there is a palpable gap between facts and opinions in modern physics. Bell’s theorem is mathematically correct, quantum predictions are confirmed beyond reasonable doubt, but there are no factual grounds to question the independence of entangled quanta. When Bell violations are obtained with incompatible properties, it does not follow that measurements influence each other. This is shown below with a toy model in which Alice and Bob achieve “super-quantum” (Popescu-Rohrlich [6]) correlations with predetermined observables. Notably, every Alice event is explicitly used twice, in combination with either measurement choice available to Bob, and vice versa. In short, there is no need for interpretations with non-locality, parallel universes, or super determinism, because there is no mystery to explain.
The skewed analysis of quantum entanglement is rooted in its conceptual history. The founders of quantum mechanics were struggling to understand the nature of non-commuting variables. How is it possible for such properties to only be real one at a time? In his quest for a new solution, Bohr suggested that quantum properties could not be pre-determined. They appeared to be fundamentally random, while being produced by independent triggers (i.e., the human choice to make one of two measurements) [7,8]. In response, Einstein argued that quantum properties existed without human intervention, as seen in correlated identical measurements [9,10]. Hence, they could be predetermined because they appeared to be simultaneously real. To sum up, Einstein and Bohr had different worldviews, but they shared the same assumption: predetermined properties must always be real at the same time. In the current age of computers, this assumption is hard to accept. We are routinely exposed to pre-programmed sequences of incompatible operations. Yet, in the early days of quantum theory, this assumption was apparently perceived as unquestionable, and it defined all the subsequent work on this topic. Even today, Bell’s inequality [11] is adopted as a universal test of locality, though it only works for jointly distributed variables. Over the years, many scientists criticized the interpretation of Bell’s theorem. To list just a few recent examples, Khrennikov exposed a contradiction between quantum theory and probability theory, if claims of non-locality are taken for granted [12,13]; Cetto and collaborators demonstrated that the bipartite quantum correlation function is local [14,15]; Raymond-Robichaud provided a general proof that any non-signaling process can be predicted by a local realist theory [16,17]. These arguments were backed by rigorous mathematical analysis, but they (like many others before them) did not seem to affect the public discourse on this topic. A possible explanation is that the underlying philosophical problem was never acknowledged. Indeed, it is very hard to grasp the relevance of such findings if “the part” is mistaken for “the whole”. The missing piece of this puzzle is that “jointly real” properties are not “everything that is real”. As will be shown below, staggered events can produce maximal violations of Bell-type inequalities with predetermined values.
2. Material and Methods
Let us imagine a typical Bell experiment, in which Alice and Bob confirm the predictions of quantum theory. When Alice measures one property (A1), while Bob has a choice between B1 and B2, can Alice’s event be the same in both cases? In practical terms, the answer is hindered by an intuitive obstacle. If Alice’s events are the same no matter what Bob does, and if Bob’s events are the same no matter what Alice does, then it feels that all the events should be real at the same time. At the very least, it seems that such properties should be compatible with each other. In other words, it should be possible to write them on the same line of an event table. Therefore, Bell’s theorem should apply, and Alice’s result should change in response to Bob’s choice to produce a violation. Surprisingly, this is not the case. A possible solution is shown in Fig. 1c below, where four “+” values and four “−“ values are placed in sequence on a “wheel of fortune”. The nuance here is that coincidences are counted for consecutive manifestations, rather than simultaneous traits. Every Alice event is flanked by two alternative Bob events. Therefore, Alice’s events are the same, regardless of Bob’s choice of observation. The same is true for Bob. However, it is a necessary feature of this arrangement that B1 and B2 values cannot be adjacent to the same value of A1. Therefore, unusual correlations are possible: A1 is correlated with B1, B1 with A2, and A2 with B2, but B2 and A1 are anti-correlated. The direct consequence of this arrangement is a maximal Bell violation.
To simulate quantum entanglement, the game requires two copies of the same wheel. Alice may get a version with Bob’s values removed, as shown in Fig. 1a, while Bob can receive a copy with Alice’s values removed (Fig. 1b). Alice and Bob can be arbitrarily close or far from each other. The only requirement is that the motion of their wheels is perfectly synchronized. Either player (or a moderator) can start the synchronous motion, while a random mechanism causes the tables to stop in a manner that cannot be predicted by the players. The wheels are also designed to end every turn on identical red dots (on the line between two adjacent sectors). Every time, Alice and Bob must record the nearest observable to the “winning” stop point, with the “+” or “−” value that happens to be in the same sector. As seen in the figure below, there are 8 possible pairwise combinations, and all of them can be fairly sampled in an ideal experiment. After accumulating a sufficiently large number of events, Alice and Bob can reconcile their lists and determine the coefficients of correlation for each of the four possible pairs: (A1,B1), (A1,B2), (A2,B1) and (A2,B2). Since the combinations are fixed in advance, given the placement of event cards on the tables, the outcome is predetermined.
A more efficient version of this game would be for Alice and Bob to record all of their events continuously, without stopping the wheels, as the relevant cards pass by the pointer on the right side of the table. In this case, an event corresponds to the center point of each card, rather than a red dot at the border. After accumulating sufficiently large data sets, Alice and Bob can meet to reconcile their events. For example, if they had a fixed rate of rotation of 1 turn per second, they must identify all the pairs of events that happened within 1/8 of a second from each other. In any version, the game can only have one result: a maximal violation of the Clauser-Horne-Shimony-Holt (CHSH) inequality [18]. Barring loss of synchronicity between the tables, the order of events is fixed, and statistical anomalies are not possible even for low numbers of turns. The same cycle of 8 events is repeated continuously. Furthermore, if Alice’s table is delayed by exactly half a period from the table of Bob, then all the coefficients of correlation switch polarity (from maximal correlation to maximal anti-correlation, and vice versa). Nonetheless, the final result is the same. The bottom line is that Bell violations are the correct theoretical outcome, without any concern about loopholes or measurement artifacts. The same Alice event is used in combination with both possible choices for Bob. The same Bob event is used in combination with either alternative outcome for Alice.
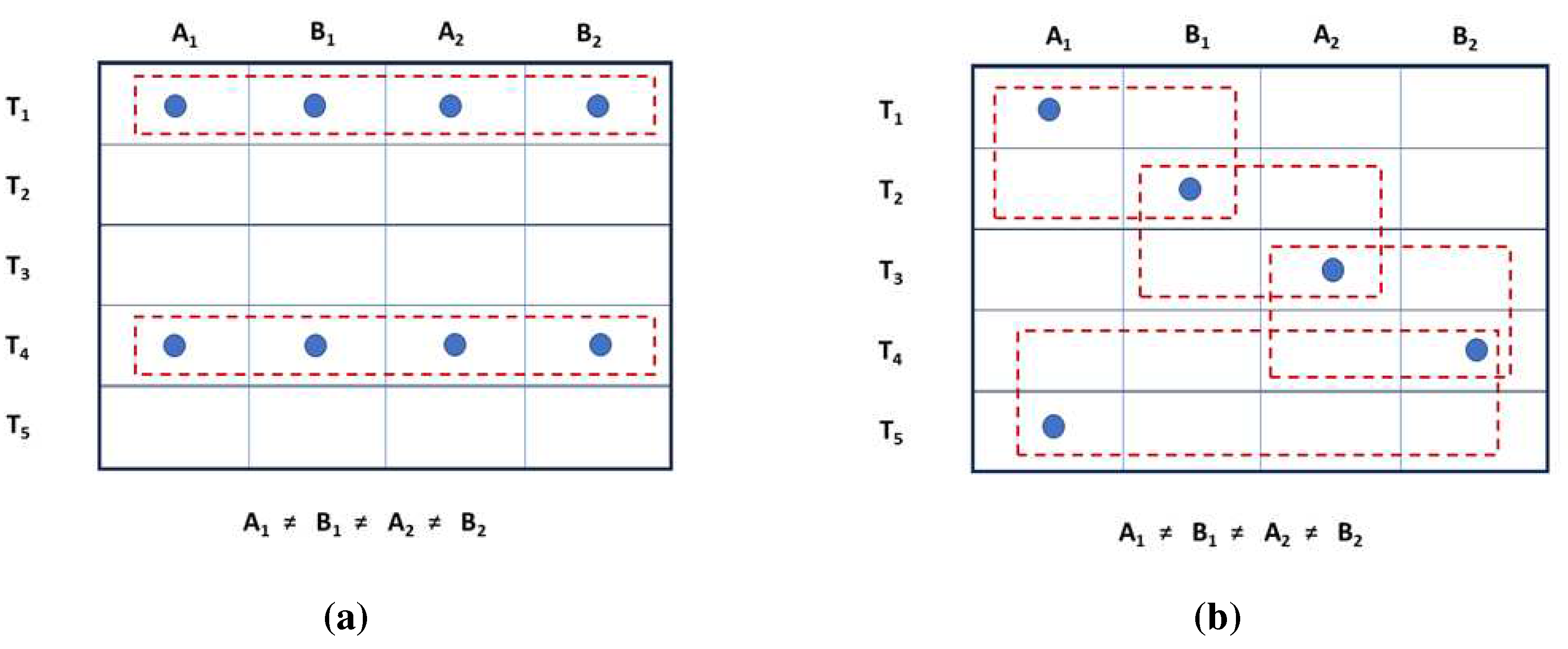
Upon closer inspection, the reason for this type of behavior is easy to grasp intuitively. When several properties occur at the same time, they obey the so-called transitive rule. For example, if we have three observables X, Y, and Z, then two pairwise correlations automatically determine the third. To visualize the logical structure of this process, consider a pile of shirts, such that “all the white shirts are made from cotton” and “all the cotton shirts are short-sleeved”. It follows with necessity that “all the white shirts are short-sleeved” in the same group. It would be a contradiction to have even one white shirt with long sleeves. Accordingly, Bell violations are logically impossible because they entail contradictory properties for one and the same object (see Figure 2a). In contrast, when we have mutually exclusive events that are staggered in time, the transitive rule does not apply. Instead, pairwise detections are restricted to adjacent events, preventing the coincidence of B1 and B2 with the same event for A1 (Figure 2b). Therefore, it is natural to have coefficients of correlation that otherwise would be incompatible. Notably, the essence of this relationship is captured by the properties of a single system. Twin systems are only needed to circumvent incompatibility for interpretive reasons.

Figure 1.
Bell experiment with correlated spinning tables. Two players, Alice and Bob, supervise the flow of events on synchronized “wheel-of-fortune” devices without interfering. The table surface is divided into 8 sectors, with 4 “+” cards followed by 4 “−” cards, as shown in image (c). Alice’s table (a) has empty sectors for Bob’s observables, while Bob’s table (b) is missing Alice’s observables. The tables are hardwired to move and stop in perfect unison. A “game host” can start the synchronous rotation, while a random mechanism forces the wheels to stop together at one of the 8 red dots. The players record the values of the observable adjacent sectors (A1 or A2 for Alice, and B1 or B2 for Bob). The goal is to analyze the correlation between coincident events, after playing the game long enough for statistical significance. Yet, the outcome is obviously predetermined. Of the 4 pairwise combinations – (A1,B1), (B1,A2), (A2,B2) and (B2, A1) – three are always correlated and one is always anti-correlated. The final result is a maximal violation of the CHSH inequality (S=4).
Figure 1.
Bell experiment with correlated spinning tables. Two players, Alice and Bob, supervise the flow of events on synchronized “wheel-of-fortune” devices without interfering. The table surface is divided into 8 sectors, with 4 “+” cards followed by 4 “−” cards, as shown in image (c). Alice’s table (a) has empty sectors for Bob’s observables, while Bob’s table (b) is missing Alice’s observables. The tables are hardwired to move and stop in perfect unison. A “game host” can start the synchronous rotation, while a random mechanism forces the wheels to stop together at one of the 8 red dots. The players record the values of the observable adjacent sectors (A1 or A2 for Alice, and B1 or B2 for Bob). The goal is to analyze the correlation between coincident events, after playing the game long enough for statistical significance. Yet, the outcome is obviously predetermined. Of the 4 pairwise combinations – (A1,B1), (B1,A2), (A2,B2) and (B2, A1) – three are always correlated and one is always anti-correlated. The final result is a maximal violation of the CHSH inequality (S=4).

3. Results
The CHSH inequality for this type of joint measurements is:
where
As described in the game, coincidence windows allow exclusively for (+,+) and (-,-) observations between three variables. Hence,
In contrast, the remaining pair is always anticorrelated, since it can only display (-,+) and (+,-) coincidences:
Accordingly, the final tally is:
This conclusion resonates with an interesting open question in quantum theory. It is well-known that quantum behavior is “non-signaling”, but can it be “non-signaling” and “non-local” at the same time? As shown by Popescu and Rohrlich [6], non-signaling events allow for maximal Bell violations (up to S=4), far beyond the known limits of quantum correlations. More recently, Raymond-Robichaud demonstrated the equivalence between local realism and non-signaling behavior [16, 17]. In other words, any non-signaling phenomenon can be predicted by at least one local realist theory. The solution described above supports this conclusion, with an important improvement: Bell violations are produced by staggered events in the same universe, as opposed to simultaneous events in parallel universes. Therefore, “super-quantum” correlations are not just “local” and “realist”. They are ordinary classical phenomena.
Furthermore, such effects are possible with pairwise joint events, but not necessarily with larger numbers of simultaneous detections. For example, it is possible to make four copies of this wheel-of-fortune, in order to detect all the properties at the same time (A1, A2, B1 and B2). In this case, observers end up producing isolated groups of four events, just as shown in Figure 2a. The cycle of staggered events is artificially broken into simultaneous bunches. As a result, the four types of events are forced to become compatible, erasing the effects of temporal mismatch between them. In this case, equation (5) becomes:
In short, Bell violations are no longer possible. Therefore, “quantum monogamy” [3] is also an ordinary classical phenomenon.
4. Discussion
Quantum theory contains numerous conditional properties. In many cases, measurement outcomes are unavoidably contextual. According to the Copenhagen interpretation, this means that physical reality is incomplete. Yet, Einstein, Podolsky and Rosen (EPR) made a strong argument that quantum theory is incomplete (not the Universe). Some outcomes are predictable without direct measurement. Therefore, quantum properties do not require observer interventions to become real. The question is how to interpret Contextuality in this case? EPR did not see it as “physically reasonable” [9] and suggested that predetermined properties are real at the same time, outside of their context. This expectation was later refuted by numerous experiments [19]. As we finally understand now, Bell’s theorem defined a clear boundary between permanent and contextual properties. Yet, why do we have to choose between Realism and Contextuality? If we assume that physical entities change their qualities objectively from context to context, then predetermined properties can become real at different times. As shown above, staggered events produce maximal Bell violations, even if they are predetermined and even if measurements are non-invasive. Therefore, quantum properties can be real and contextual at the same time. This means that quantum theory is correct, as insisted by Bohr, and ontologically incomplete, as shown by Einstein. The two sides can finally shake hands in agreement.
The overlooked detail of quantum entanglement is that non-commuting variables are never real at the same time. They seem to be observable at the same time with two correlated systems, but the relevant effects are still determined by incompatible mechanisms of preparation. If both systems are prepared in the same way, then Alice and Bob are forced to make their measurements at different stages of quantum propagation (or else they can only measure identical properties). Hence, twin systems produce the same type of correlations that would be obtained in a single system if consecutive non-destructive measurements were possible. Though, as shown above, maximal Bell violations require ideal experiments. The delay between paired measurements must be constant, such that any combination of two observables can fall within the same coincidence window. Furthermore, positive (negative) values have to be grouped together, ensuring maximal coefficients of correlation between adjacent events. Finally, the largest violations are possible when there is a sudden shift from the positive to the negative domain (and vice versa), emphasized with different colors on the “wheel of fortune”. There is an instructive difference between the solution presented above and the known features of actual photon polarization (or other spin-like measurements). In these cases, there is a gradual increase in phase delay between optical components, as the angle between measurements is increased. Real Bell experiments maintain constant differences between observables by choosing four measurements at equal angular intervals from each other (22.5°). Furthermore, rotations of the plane of polarization introduce a gradual (and non-linear) loss of correlation, as dictated by Malus’ Law. This explains the gap between the maximal Bell violations that are numerically possible and the ones that are theoretically possible for wave-functions. Accordingly, it is now possible to resolve the ongoing debates about the limited nature of quantum correlations. From the perspective of Bell’s argument [11], the apparent problem was that quantum correlations were “too high”. Yet, as suggested by Popescu and Rohrlich [6], the true physical puzzle was that they were “too low”. As it turned out, there is nothing special or non-classical about Bell violations, be they “quantum” or “super-quantum”. Indeed, it is misleading to describe these correlations as “quantum”, because they are natural properties of classical beams as well [20].
A favorable condition for the discovery of this solution was the decision to treat “quantum nonlocality” and “quantum monogamy” as a single problem. Though, it took a few tries to get here. Under the influence of real details from loophole-free experiments, an earlier proposal was to consider possible correlations between simultaneous random events, modulo the probability of coincidence [21]. Intuitively, single events are more probable than double events, which are more likely than triple events, and so on. This explained the emergence of incompatible pairs of events, with quantum monogamy as a subset of this pattern. Unfortunately, such a solution could not work for classical projections, where Bell violations and “Bell monogamy” are both possible for ideal measurements, without down-selection or loss of energy. Indeed, as shown above, a better solution was waiting to be found. This shows that quantum experiments are not always the best way to get insights on quantum behavior. Sometimes, the best strategy is to study classical wave mechanics, while keeping in mind that it is still a work in progress.
The mechanism behind quantum correlations may seem straightforward and simple, especially in retrospect. Yet, before even opening the path towards this solution, the challenge was to sort out the wave and particle aspects of quantum behavior. Solid bodies, such as bowling balls, have simultaneous values for momentum and position at every stage of motion. In contrast, waves are collective phenomena, with typically undefined spectra for momentum and position. As shown with Fourier analysis, the spectrum of position can only be well-defined in a plane of measurement where the spectrum of momentum is maximally undefined, and vice versa. The two planes can emerge in sequence, for example when a beam of light is passed through a lens [22]. Apparently, quanta are discrete objects and should exhibit particle qualities. Yet, quantum theory predicts “wave-function” properties. Individual quanta can only produce incremental knowledge about discrete points in wide distributions of co-planar events. In other words, quantum experiments do not “inspect” quanta for intrinsic momentum and position. Instead, they determine the relative number of quanta at different coordinates of measurement, in order to confirm the amplitude of the corresponding wave-function. Hence, by travelling across different planes of measurement, a quantum is able to produce information about different incompatible properties, in sequence, in the event that it is absorbed by a detector. A very helpful demonstration of this phenomenon was provided by the realization of the EPR gedankenexperiment with entangled photons at Rochester University [23]. In order to confirm momentum correlations, entangled quanta had to be detected in the focal planes of corresponding lenses (one in each channel). In order to verify position correlations, detectors had to be pushed back to the conjugate image planes. In other words, quanta did not transform under scrutiny in the same context of observation. They provided alternative bits of knowledge at consecutive stages of propagation. Accordingly, the solution to the EPR paradox is to assume that entangled quanta reveal conditional knowledge about each other. Measurement outcomes are predictable with certainty, but only for transient contexts of observation. This insight (and maybe twelve more years of sustained investigation) lead to a moment of epiphany about the statistical difference between consecutive and simultaneous properties. With such a solution in hand, finding an adequate toy model was merely a matter of technical follow-through.
5. Conclusion
Bell violations cannot be used as markers for locality. They only serve to differentiate between properties that can be simultaneously real (as part of a single system) and properties that cannot. As shown above, CHSH violations are classically possible for the full range of non-signaling correlations. This was demonstrated with a concrete mechanism, in which measurement outcomes were explicitly fixed for any possible pairwise combination. The hard part was to discover that staggered events and simultaneous events can have different rules of pairwise combination. This result does not contradict quantum theory. It only refutes the interpretations that distorted its physical essence. In hindsight, the concept of “quantum nonlocality” emerged as the result of a single error. Predetermined events were expected to be simultaneous in any “reasonable” description of reality. This assumption was explicit in the EPR paper and implicit in Bell’s Theorem. Accordingly, a single correction is required to fix the problem, with all of its complex ramifications.
Acknowledgments
The search for this solution was inspired by a series of discussions with Jan-Åke Larsson, Gregor Weihs, Sergey Polyakov, Andrei Khrennikov, Ana-María Cetto, Richard Gill, and France Čop.
References
- J. A. Wheeler and W. H. Zurek (eds), Quantum Theory and Measurement (Princeton, 1983).
- Peres, A. Quantum Theory: Concepts and Methods (Kluwer, 1993).
- Dhar, H. S.; Pal, A. K.; Rakshit, D.; Sen (De), A.; Sen, U. “Monogamy of Quantum Correlations - A Review”. In: F. Fanchini, D. Soares Pinto, and G. Adesso (eds), Lectures on General Quantum Correlations and their Applications (Springer, 2017).
- Fine, A. Joint Distributions, Quantum Correlations, and Commuting Observables. J. Math. Phys. 23, 1306 (1982). [CrossRef]
- Kujala, J. V.; Dzhafarov, E. N.; Larsson, J-A. Necessary and Sufficient Conditions for an Extended Noncontextuality in a Broad Class of Quantum Mechanical Systems, Phys. Rev. Lett. 115, 150401 (2015). [CrossRef]
- Popescu, S.; Rohrlich, D. Quantum Nonlocality as an Axiom. Found. Phys. 24, 379 (1994). [CrossRef]
- Bohr, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 48, 696 (1935). [CrossRef]
- Jammer, M. The Conceptual Development of Quantum Mechanics (McGraw Hill, 1966).
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47, 777 (1935). [CrossRef]
- Einstein, A. Physics and Reality, in Einstein, A. Ideas and Opinions, 290-323 (Crown, 1954). [CrossRef]
- Bell, J. S. Speakable and unspeakable in quantum mechanics (Cambridge UP, 1987). [CrossRef]
- Khrennikov, A. Bell-Boole Inequality: Nonlocality or Probabilistic Incompatibility of Random Variables? Entropy, 10, 19 (2008). [CrossRef]
- Khrennikov, A. Get Rid of Nonlocality from Quantum Physics. Entropy 21, 806 (2019). [CrossRef]
- Cetto, A. M.; Valdés-Hernández, A.; de la Peña, L. On the Spin Projection Operator and the Probabilistic Meaning of the Bipartite Correlation Function. Found. Phys. 50, 27 (2020). [CrossRef]
- Cetto, A.M. Electron Spin Correlations: Probabilistic Description and Geometric Representation. Entropy 24, 1439 (2022). [CrossRef]
- Raymond-Robichaud, P. The Equivalence of Local-Realistic and No-Signalling Theories. Preprint: arXiv:quant-ph/1710.01380. https://arxiv.org/abs/1710.01380. [CrossRef]
- Raymond-Robichaud, P. L’équivalence entre le local-réalisme et le principe de non-signalement. PhD Thesis (Université de Montréal, 2017). https://papyrus.bib.umontreal.ca/xmlui/handle/1866/20497.
- Clauser, J. F.; Horne, M. A.; Shimony, A.; Holt, R. A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 23, 880 (1969). [CrossRef]
- Rosenfeld, W.; et al. Event-Ready Bell Test Using Entangled Atoms Simultaneously Closing Detection and Locality Loopholes, Phys. Rev. Lett. 2017, 119, 010402. [CrossRef]
- Mardari, G. N. Experimental Counterexample to Bell’s Locality Criterion. Entropy 24, 1742 (2022). [CrossRef]
- Mardari, G. N. How to Erase Quantum Monogamy? Quantum Rep 3, 53 (2021). [CrossRef]
- Hecht, E. Optics (Addison-Wesley, 2001).
- Howell, J. C.; Bennink, R. S.; Bentley, S. J.; Boyd, R. W. Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett., 92, 210403 (2004). [CrossRef]
Figure 2.
Simultaneous and staggered events can have different rules of pairwise combination. Some patterns of coincidence cannot violate Bell-type inequalities. As shown in table (a), simultaneous events are blocked into fixed groups. The same event is paired repeatedly with any other observable. Therefore, corresponding coefficients of correlation do not contradict each other. In contrast, staggered events allow for pairwise combinations outside of the group. As seen in table (b), it is impossible for four different events to be adjacent to each other. Instead, a narrow window of coincidence forces the emergence of incompatible pairings. On the other hand, if four different events are recorded at the same time, this pairwise inconsistency is erased, and pattern (b) switches back to pattern (a). Thus, “quantum correlations”, “super-quantum correlations” and “quantum monogamy” are classical phenomena.
Figure 2.
Simultaneous and staggered events can have different rules of pairwise combination. Some patterns of coincidence cannot violate Bell-type inequalities. As shown in table (a), simultaneous events are blocked into fixed groups. The same event is paired repeatedly with any other observable. Therefore, corresponding coefficients of correlation do not contradict each other. In contrast, staggered events allow for pairwise combinations outside of the group. As seen in table (b), it is impossible for four different events to be adjacent to each other. Instead, a narrow window of coincidence forces the emergence of incompatible pairings. On the other hand, if four different events are recorded at the same time, this pairwise inconsistency is erased, and pattern (b) switches back to pattern (a). Thus, “quantum correlations”, “super-quantum correlations” and “quantum monogamy” are classical phenomena.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Maximal Bell Violations with Independent Classical Observables
Ghenadie Mardari
,
2024
Proposed Solution to the Quantum Randi Challenge
Ghenadie Mardari
,
2023
Experimental Counterexample to Bell’s Locality Criterion
Ghenadie N. Mardari
,
2022
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







