Prerpints.org logo
Preprint
Article

An ESR Study Comparing Nanometer-Nanosecond Dynamics in Diblock Copolymers and Their PMMA Binary Blends

Altmetrics

Downloads

88

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 September 2023

Posted:

21 September 2023

You are already at the latest version

Alerts
Abstract
Block copolymers are a class of materials particularly interesting for their ability to self-assemble into ordered structures. In this context, the coupling between environment and dynamics is particularly relevant, given that movements at the molecular level influence various properties of macromolecules. Mixing the polymer with a second macromolecule appears to be an easy way to study these relationships. In this work, we studied a system based on two diblock copolymers of methyl methacrylate as first block and 3-methyl-4-[6-(methylacryloyloxy)-hexyloxy]-4’-pentyloxy azobenzene as second block and their blends with PMMA. The relaxational properties of these systems were investigated by electron spin resonance (ESR) spectroscopy sensitive to nanometric length-scales. The results of the study on the blends were related to the dynamic behavior of the copolymer. The study evidenced the presence of fast and slow molecular sites for the molecular reorientation at nanoscale, modulated by the ability of block copolymer to form supramolecular structures. For blends, the heterogeneities at nanoscale are still detected. However it was found that the presence of the PMMA as the major component of the blends modified their dynamic behaviour.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

Block copolymers are an interesting class of single component polymeric materials [1], that cannot macrophase separate. However, the chemically incompatible blocks covalently linked lead to a local microphase segregation on the length-scale of the copolymer chains and self-assembling [2] (pp. 24-130). Their bulk organization can exhibit various morphologies [3,4,5] at nanoscopic length scales; the typical dimensions of the microdomains are ranging from 5 to 50 nm [6], a span that encompasses those required for a quite extensive range of potential applications [7,8,9].
Research progress in materials chemistry has provided polymerization techniques [10,11,12] giving the opportunity to an enormous variety of accessible polymer architectures ranging in complexity and with controllable multifunctions [7,9,13]. Block copolymers containing liquid crystalline (LC) moieties have attracted scientific and industrial attention because of the possibility of adding orientational ordering to the morphological characteristics of block copolymers [14]. Their potential applications span in the fields of biology, photonics, nanotemplates and nanofabrication processes [7,15,16,17,18,19].
A special class of LC block copolymers contains blocks with side-chain liquid crystalline (SCLC) units, namely blocks with an amorphous backbone and mesogenic units attached to it as side-chains, typically through an alkyl spacer [20]. A relevant unit that can be used as mesogenic group in SCLC block copolymers is the azobenzene chromophore [21]. Indeed, polymers containing azobenezene have been intensively studied as promising photonic materials due to their controllable properties in response to light [22,23]. Repeated trans−cis−trans cycles of the azobenzene chromophore within a polymer matrix can generate reversible processes of photoorientation, photoselection, and photomodulation from the molecular level over several spatial and temporal length scales. Then, the photoreaction is accompanied by a molecular reorientation that might be applicable to rewritable optical and holographic memories [24]. Azo-based polymers have been demonstrated to be suitable candidates for all-optical reversible information data storage at both micrometer and nanometer length scales. [25,26].
With the aim of obtaining increased information storage with respect to films of azo-containing homopolymers, enhanced performance could be obtained by the azobenzene block copolymers. In fact, microphase separation in nano blocks is a favouring factor for the performance of optically driven nano-modifications [27,28,29] from one hand leading to a long term and high reliability storage of the light-induced nanowrited information and, from the other hand, allowing both to decrease the optical absorption of azobenzene units and to extend the possibility of information storage over the complete thickness of the sample [14,25]. With this respect, another interesting approach is provided by blending procedure, which is a general way largely in use [30,31,32] for achieving a specified portfolio of physical properties, without the need to synthesize specialized polymer systems. As an example, azobenzene block copolymers blended with a polymer similar to one of the blocks have been prepared to increase dilution of azobenzene moieties as well as to control the microstructure of micro-segregated copolymers. Their optical properties were investigated and characterized for optical storage purposes [33,34].
As a general feature, a recording medium suitable for all-optical reversible information data storage should exhibit a series of properties [24], such as optical quality, sensitivity, dynamic range, optical absorption, bit stability, homogeneity at molecular level and working temperature [35,36].
Accordingly, dynamics at the nanoscale is an important issue for the formation and stabilization of microstructures and relaxation processes and its study appears a pivotal topic to understand and characterize the materials.
In this respect, electron spin resonance (ESR) spectroscopy is an important technique for the study of dynamics and local structure of simple [37,38] and complex [39,40,41,42,43] materials. In particular, ESR spectroscopy turns out highly sensitive to the segmental motion of polymer chains which, in turn, can modulate the macroscopic properties and performances of polymers. ESR studies in diamagnetic systems are often carried out by dissolving very small quantities of paramagnetic centers, so called spin probes, [44,45] whose size and shape select the length scale of the experiment. Among nitroxides spin probes, cholestane was profitably employed in literature to assess molecular motion because its ESR spectrum is sensitive to morphology and dynamics of the environment [36,44,45,46].
ESR spectroscopy has been profitably exploited to study different segmental dynamic responses at the nanoscales both in time and in length, allowing to obtain plenty of information. Using ESR, it was possible to detect heterogeneity and stability at the nanoscale of different molecular sites in polymers [37,47]. ESR investigations were able to reveal connections between nanoscale dynamics with chain dynamics or local relaxation, associated with signatures and dynamic anomalies in the temperature dependence of the times of the molecular reorientation [46,48,49,50,51,52].
The present work reports on an ESR study of two block copolymers composed by methyl methacrylate (MMA) first block and an azobenzene-based methacrylic (MA4) second block, either alone or blended with PMMA. The focus is on dynamics at the nanoscale, which is a pivotal topic for the formation and stabilization of microstructures and relaxation processes in these materials, with the aim to unambiguously establish the distinct response of local dynamics as consequence of matrix heterogeneity and changes in environment. We highlight how the different morphology results in different matrix heterogeneities with very different dynamic responses at the nanoscale.

2. Materials and Methods

2.1. Materials

Diblock copolymers of the nematogenic 3-methyl-4-[6-(methylacryloyloxy)-hexyloxy]-4’-pentyloxy azobenzene MA4 monomer and methyl methacrylate MMA, (Figure 1, Table 1) were prepared according to reported procedures [27,53].
The MA4 repeat unit has a molar mass of 468 g mol–1 and a side-chain length of about 30 Å (evaluated with ChemSketch). The MMA repeat unit has a molar mass of 100 g mol–1 and a side-chain length of about 2.5 Å (evaluated with ChemSketch). Diblock copolymers with well defined structure and low molar mass dispersion were obtained by atom transfer radical polymerization (ATRP), according a two step procedure. In particular, in the first step a PMMA macroinitiator (Table 1, average degree of polymerization 200 and standard microstructure as 60% syndiotactic, 35% atactic and 5% isotactic) was synthesized and then used for the polymerization of MMA.
Blends of the copolymers with a PMMA homopolymer, the same used as macroinitiator, were prepared by codissolution of the corresponding amounts of both components in dry dichloromethane. The final content of the azobenzene units in the blends was 5% by weight.
A conventional nomenclature was adopted in order to refer to diblock copolymers, Bx, where the index x denotes the 20% or 10% mole fraction of MA4 co-units in the copolymer, (Figure 1). The 5% blends are indicated by adding b5 prefix to the diblock copolymer names, so blends will be referred to as b5B10 and b5B20.
Average molar masses and molar mass distributions of diblock copolymers (Table 1) B10 and B20 were determined by size-exclusion chromatography (SEC) [27]. However, the absolute values of the molar masses in the distribution of these copolymer samples may differ by 10% from the respective SEC values [55]. DSC curves of diblock copolymers were recorded with a Mettler Toledo DSC30 calorimeter on heating from about 225 K at 10 K min−1 after cooling at 20 K min−1 from about 473 K.
The copolymers were liquid crystalline and a nematic-to-isotropic transition temperature TNI was found. Also, they exhibited two Tgs: TgPMMA and TgPMA4 as expected for microphase separated block copolymers [56].
Investigations in diblock copolymers by means of atomic force microscopy showed that the copolymers were microphase separated up to an order-to-disorder transition (TODT) (Table 1) [27]. In binary blends of an homopolymer with a block copolymer, the phase behaviour is controlled by the lenght of the homopolymer chain in comparison with the copolymer [2] (p. 332). In general, considering the number average degree of polymerization NAh of the homopolymer A, and NAc, the one of the same component in the copolymer, it is found that the homopolymer is selectively solubilized in the A microdomains if NAh ≈ NAc, however with the tendency of remaining in the middle of the A microdomains. As a consequence the conformations of the chain B, namely the one of the other block of the copolymer, are not perturbed significantly. In all the present blends, the ratio between the number average molecular weights (or the degrees of polymerization) of the homopolymer and the corresponding block in the copolymer ρ = MAh/MAc = NAh/NAc = 1, so we expect the permanence of the microphase separation in the blends [2].

2.2. Rheological characterization

The viscoelastic characterization of diblock copolymers was carried out with an Anton Paar Physica MCR301 rheometer by means of a plane-plate sensor system (25 mm diameter). The temperature of the samples was stable within 0.1 K (CTD450 temperature unit). Oscillatory and creep-recovery experiments were performed, all the measurements being gap-independent. The applied stress intensities were chosen to perform measurements in the linear viscoelastic regime response. Creep and creep-recovery experiments were carried out without breaking the linear viscoelastic limit and performed in order to evaluate zero-shear viscosity [57] (pp. 419−464), [58]. In oscillatory experiments, isothermal frequency sweeps were usually performed in the range from 10–3 Hz to 24.4 Hz. However, on approaching Tg, the lower limit was extended down to 10−4 Hz.
Rheological material functions were investigated in the copolymers, from temperature above Tg PMA4 up to high temperatures, in the flow region for B10 and B20.
No discontinuity was observed in the investigated temperature range [59], not even across TNI and TODT. However, the different chemical and structural arrangement of the block copolymers led to the failure of the time temperature superposition (TTS) principle [57] (pp. 486−491), [58].
The viscosity was evaluated by creep-recovery experiments, its temperature dependence was profitably fitted by a Vogel-Fulcher-Tamman (VFT) law [60]
η (T) = η ∞ exp [Tb/T-T0]
Pseudoactivation temperatures Tb and Vogel temperatures T0 are given in Table 2 [61].
In spite of the thermorheological complexity of B20 and B10 samples, in oscillatory experiments it was possible to collapse to a single master curve the G' component of the complex shear modulus G*, by superimposing isothermal frequency sweeps. This could be ascribed to the blocky nature of the copolymers for which the different temperature dependence of the monomeric friction coefficients affects to a greater extent the viscous properties rather than the elastic ones [59].
In Table 2, the fitting parameters according to a VFT dependence are also reported for the shift factors a(T) [62] of G' .
The presence of different mechanisms driving elastic and viscous behavior in these di-block copolymers is confirmed by non-coincident values of the VFT parameters for η and a(T) of Table 2 [61].
Data of the rheological behaviour of a PMMA sample of similar molecular tacticity were taken from literature [54].
Because of the tiny amount of available sample it was not possible to carry out rheology measurements over blends.

2.3. ESR - Apparatus and Experimental Technique

ESR measurements were carried out by means of a continuous wave Bruker ER200D-SRC spectrometer operating in the X-band, equipped with an X band bridge (Bruker ER042-MRH) and a NMR gaussmeter ER035M. The temperature was controlled (Bruker BVT100 gas-flow unit) with nominal accuracy of ± 0.1 K.
ESR studies were performed on samples in which the paramagnetic molecular tracer cholestane was dissolved. All samples were prepared at room temperature by mixing two chloroform solutions, each of them containing a predetermined amount of copolymer or related blend and molecular probe. The resulting solutions had a concentration of about 10-3 cholestane/repeat unit molar ratio. The samples were then evaporated to complete dryness by being heated under vacuum at a proper temperature, and finally sealed in a standard ESR tube.
The structure of cholestane (3 β-doxyl-5 α-cholestane, 98%, Aldrich) nitroxide spin probe is shown in Figure 2. It was adopted because of good thermal stability and because its stiffness and shape make it suitable to probe anisotropic media [36,50,51,61,63,64].
It can be sketched as a prolate ellipsoid with semiaxes of about 0.99 nm and 0.29 nm [65]. Its size selects the sensitivity of the ESR experiment at the nanometer scale [36,50,51], relevant to detect heterogeneous morphology and dynamics of cooperative processes in materials [66]. Moreover, the ESR lineshapes of cholestane tracer are determined by rotational correlation times falling in the nanosecond time scale of molecular motion, characteristic of dynamics of complex systems [51,67,68].
The cholestane rotational dynamics is described in terms of the diffusion model under cylindrical symmetry [49,69,70]. Accordingly, a spinning diffusion coefficient D|| characterizes the rotation along the symmetry axis of the molecule and a tumbling diffusion coefficient D⊥ accounts for the rotation of the axis itself [71,72]. The ratio D||/D⊥ resulted to be close to 15 for cholestane in all the investigated copolymers and blends. For comparison purposes with the results of rotational dynamics reported in literature [36,46,61], [44] (pp.60-63), in this work the reorientation of cholestane is discussed in terms of a spinning correlation time, defined as τ||=1/(6D||) [44] (pp.60-63), [73,74].
The values of the cholestane principal components of the Zeeman and hyperfine magnetic tensors, in the molecular frame [44,75], are reported in Table 3, where for completeness the principal component of PMA4 homopolymer (Figure 1, x = 100 mol%) [36] and a PMMA (Figure 1, y = 100 mol%) homopolymer sample are reported [76].
They were obtained by simulation of ESR lineshape in the ultraslow motion regime [77], according to a procedure detailed elsewhere [69].
More details about the experimental procedure and the ESR technique can be found elsewere (see for example: [48] and references therein, SI of [61]).

3. Results and discussion

3.1. ESR lineshapes

As a first step, ESR experiments were carried out to check the presence of memory effects related to the thermal history of the samples. Figure 3 (a) shows the experimental ESR spectra for B10, recorded at the beginning and at the end of annealing at the temperature Ta=387 K, set in the isotropic state of the liquid-crystalline copolymer. The lineshapes for b5B10 blend at the start and end of annealing at Ta = 400 K are also shown on the Figure 3 (b). None of the copolymers and blends of this work exhibited any thermal history dependence [36,61], therefore the study was carried out recording the spectra at the selected temperatures without any thermal treatment.
These findings differred from what reported in previous studies [36,46,61] on liquid-crystalline PMA4 random copolymers and homopolymer (x = 100 mol% in Figure 1), where memory effects affected the stability of the ESR lineshape, with a redistribution of the spin probe between different local environments.
The stability of the site in diblock copolymers and blends is probably owed to the small perturbation induced by the ordering of mesogenic units in the liquid-crystalline phase . This results seems to confirm the literature results [78] on polymers similar to the ones of the present study, where it was found that the morphology of the microphase of the block copolymers containing side-chain liquid-crystalline units was not influenced by liquid-crystalline order.
The lineshapes of Figure 3, while referring to a sample with a relatively small amount of mesogenic MA4 counit, signal the presence of two sites, a slow and a fast one, for the probe reorientation in the polymer matrix, as pointed out by the vertical dotted lines reported on the left side of Figure 3.
All recorded lineshapes were carefully simulated. The procedure quantitatively confirmed the bimodal character of the distribution function of the spin probe sites. In particular, the best simulation of the ESR spectra [36,79] was provided by a two δ - like distribution function, with a fast and a slow dynamic component.
The ESR study in samples with B20 or B10 copolymer as minor component in the PMMA-based blends showed that the experimental lineshapes of blends were coincident at same temperature, within the experimental errors. Accordingly, the lineshapes and dynamic results presented in this work refer to both b5B10 and b5B20 blend samples.
With respect to experiments on diblock copolymers recorded at the same temperature, ESR lineshapes of blends turned out mostly dominated by the properties of PMMA major component, exhibiting spectra shifted towards the slow motion dynamics.
This is seen by comparing the lineshapes of B20, B10 and blend samples recorded at the same temperature T= 415 K (Figure 4), where the blends present a lineshape pertinent to a dynamics slower than the one of both diblock copolymers. This is recognizable by the structures at high and low values of the magnetic field uppermost on the overall lineshape. In particular, at temperatures less that 353 K, blend lineshapes were characterized by the time-scale of ultraslow motion, where the ESR spectroscopy is insensitive to details of molecular motion [51] (and references therein); then the study of their rotational dynamics was investigated from temperatures greater than about 350 K.
So it appears clearly that ESR spectroscopy is able to reveal features of dynamics at a time-scale where local heterogeneity develops, as a consequence of the polymer architecture and microstructure.

3.2. Rotational dynamics

3.2.1. Behaviour with temperature

The spinning correlation times of cholestane in diblock copolymers were investigated in a range of temperatures that exceeds TNI, and are shown in Figure 5. The presence of fast and slow sites for the probe reorientation indicates that the probe dynamics experiences the presence of the MA4 blocks, independently of their concentration [46,61]. In particular, the dynamic heterogeneity was attributable to the actual microphase separation of these diblock copolymers, and to submicron/nanoscale domains formed by the nematogenic MA4 blocks, also at low concentrations. They favor the segregation of a part of molecular tracers into the domains of the minority phase or provide a probe redistribution among the block components above TODT.
This analysis is supported by the comparison with results of ESR dynamics in random copolymers of same co-units and comparable molar concentration [46,61]. In these experiments, ESR evidenced instead a homogeneous reorientation, as a consequence of the different architecture of the environment at nanometer scale.
The rotational dynamics shown in Figure 5 attests the similar behavior, both in shape and in magnitude, of the correlation times with temperature in the two copolymers.
For the investigated temperatures, greater than TgPMA4 (Table 1), the reorientational dynamics in the different separated microphases was characterized. For slow and fast sites, two dynamic regions were identified that were referred to as the intermediate (IT) and the low (LT) temperature regimes (Table 4), in analogy with a nomenclature adopted in previous studies on random copolymers [61]. IT and LT dynamic regions are separated by a dynamic anomaly.
The Arrhenius plot of ESR correlation times in blends is reported in Figure 6 and accounts for their heterogeneous dynamics with two sites available for the cholestane reorientation in the whole investigated range of temperatures. Note that the simulation of the blend lineshapes provided a population of fast sites tiny and active in the whole investigated temperature range, always maintaining itself almost constant at a mean percentage of about 13%.
Figure 6 shows that, unlike diblock copolymers, fast and slow dynamic sites exhibit different temperature behaviors in the whole investigated range.
It appears that no dynamic anomaly was detected for the fast correlation times of the tracer rotation. Interestingly enough, an eye-guide in the figure suggests a trend toward a collapse to a homogeneous dynamics at the temperature TNI (Table 1), somewhat establishing a correlation of the fast site dynamics with the LC co-units as the minor component in the blend.
The slow sites presents a dynamic trend that parallels the one of diblocks copolymers, with a dynamic anomaly separating different behaviours of the rotational correlation with temperature.
As already noted on Figure 4, these correlation times are slower than the ones of diblock copolymers. A comparison with ESR correlation times of neat PMMA component of the blends is not available, because its lineshapes fall in the ESR ultraslow motion regime, where dynamical information are not accessed by the spectroscopy. However, in Figure 7 the slow blend dynamics is confronted with correlation times by ESR experiments carried out for the same temperatures in a PMMA4900 polymer [76] with lower mass and identical standard structure composition.
The figure shows, for comparison purposes, also the slow dynamics of B10 and B20. It appears that correlation times of PMMA4900 and blends fall in the same range of values, suggesting that the mechanisms of relaxation of the PMMA, as major component of the blends, drives the slow correlation loss of molecular probe, while the presence of a minor component in the blends makes the information of the dynamics available to the spectroscopy, by fastening the overall relaxation of the material.
The simulation of the heterogeneous ESR lineshape of diblock copolymers also provided the behaviour of the population of dynamic sites over the measuring temperature range. An example is shown for B10 in Figure 8, where one can appreciate that, differently from blends for which a constant population was found, different regimes can be detected. At temperatures well above both TODT and TNI, the mean percentages of fast sites level off at plateau values, dependent on the percentage of MA4 co-units. In particular, it is found 60% for B20 and 50% for B10, so the higher the content of mesogenic co-units, the higher the amount of percentage of fast sites in the sample. On lowering temperature, an increase in the percentage of fast sites is detected at TODT temperatures, suggesting that the ordering process, taking place in nonmesogenic constituent of the block copolymers, makes available more free volume for its mesogenic part, where most molecular tracers are placed [61], at these temperatures. Then, as temperature further decreases towards TNI, the population of fast dynamic component decreases smoothly and progressively indicating that the increasing tendency towards the nematic ordering in the LC block of copolymer reduces the available free volume at the mesogenic units and pushes the molecular probe to move away from it.

3.2.2. Discussion

As a first step, let's consider the presence of dynamic anomalies observed in Figure 5 and Figure 6, that separate different temperature dependences of correlation times (Table 4). As far that, crossover temperatures between different dynamic regimes are not an unusual finding in complex systems. For example, they were also detected by ESR studies in random copolymers of the same co-units [61] at a temperature about 1.2 TgPMA4 , as a signature of different dynamical regimes. Also literature studies have provided evidence [67,80] that the temperature 1.2 Tg signals dynamic anomaly in molecular glass formers and linear homopolymers [76] (and references therein), and it is usually related to the onset of cooperative processes in materials.
In the case of the diblock copolymers under investigation, the dynamic anomaly locates at about 1.2 TgPMA4, in the interval between TgPMMA and the order-to-disorder transition temperature TODT of block copolymers (Table 1).
This finding suggests that a collection of different interactions can play a synergistic role in setting the crossover temperature of diblock copolymers, such as, on heating, the emergence of the collective processes of polymeric relaxation at temperatures above the PMMA glass transition of copolymer and the onset of cooperative processes related to the softening of the supramolecular structure and of nanodomains of minority phase.
Regarding blends, the dynamic anomaly in slow sites is observed at about the temperature TgPMMA as detected in B10 and B20 copolymers and in PMMA (Table 1 and [54,81]). This indicates that slow dynamics in blends is mainly driven by the coupling of the molecular probe to the α relaxation of the main chain, and confirms what was argued with reference to Figure 7.
Crossover temperatures separate intermediate (IT) and the low (LT) temperature regimes.
At temperatures below the crossover, the dynamics follows an activated Arrhenius regime (Table 4)
τ||(T) = τ|| ∞ exp [ΔE/(kBT)],
The presence of a thermally activated regime seems to indicate that collective relaxation has become too slow to drive the rotational diffusion of the probe molecule, and that, instead, at this stage a coupling is expected [82,83] with less cooperative and more closely localized relaxation mechanisms. In the present case, they equally affect and drive both dynamic sites in diblock copolymers as well as slow sites in blends.
The activation energies ΔE are about 13 kJ mol−1 (Table 4), and result similar to the ΔE values found in random copolymers [61] of same co-units. Interestingly enough, ΔE shows values characteristic of the cholestane or other molecular tracers in molecular glasses [84,85,86] or oligomers [51,87], for which local segmental processes drive the activation regime of the "cage" where the probe is located and for which ΔE ranges from 10 kJ mol−1 to 22 kJ mol−1.
The activation energy of the present copolymers and their blends do not agree with values reported for low polymers of PMMA investigated either by ESR [76], or for studies on PMMA by dielectric or mechanical methods [82] (p.258), [83]. However, it has to be noted that an ESR literature study carried out on a spin labeled PMMA detected activation energies of values comparable with the findings of this work [88] for measurements carried out in the same range of temperature.
Therefore, considering the values of activated processes of a label chemically attached to PMMA and the ones of random copolymers of same co-units but with a small or an absent amount of fast population [61], one can argue that these localized mechanisms pertaining to LT regions of slow relaxation are to be drawn back to the cage stiffness and constraints affecting the molecular tracers in PMMA regions of the copolymers and blends. Moreover, a possible signature of the effects of the supramolecular order constraining the phase separated nanodomains of the diblock copolymers can be recognized by noting that these relaxation mechanisms mantain equally effective also on fast time scale of probe dynamics of block copolymers.
In diblock copolymers, as the temperature increases, the ordered microstructure softens and then vanishes, so that, at temperatures higher than TODT >TgPMMA, the dynamics has become somewhat sensitive to a less localized collective relaxation of the polymer matrix. Then, a VFT (equation 3) temperature dependence of correlation times is observed:
τ||(T) = τ|| ∞ exp [Tb/T-T0],
VFT dynamic regions, Vogel temperatures T0 and activation pseudo-activation temperatures Tb are reported in Table 4.
In the eventuality of virtual coincidence of T0 from ESR measurements and viscosity, the degree of coupling between macroviscosity and microviscosity, at the level of segmental friction, namely between rotation and viscosity, can be evaluated by expressing the spinning correlation time as a power law of the viscosity:
τ||(T) ∝ [η (T)]ξ,
where ξ, the fractional exponent, may vary between 0 and 1, with ξ = 1 corresponding to a complete coupling of the probe dynamics to the terminal relaxation of the host matrix. ξ resorts to be the ratio of the Tb of the VFT law relevant to the dynamics of the rotational dynamic component over the value of the pseudo-activation temperature pertinent to the sample viscosity.
The occurrence of complete coupling between the spin probe reorientational dynamics and structural relaxation processes or viscosity in the polymeric matrix has been demonstrated just in a very few cases [47,51,76]. In the IT dynamic range with liquid crystalline units, the decoupling, manifesting itself by an exponent ξ lesser than the unity, was interpreted as outcome of coexistence of steric and cooperative effects [36,61].
In the present case, B10 and B20 diblock copolymers show thermorheological complexity [89] and viscosity η and shift factor a(T) may not present coincident values of the T0 values pertaining to the two different material functions (Table 2).
Comparing T0 temperatures from ESR (Table 4) and the ones from rheology (Table 2), it is seen that both dynamic sites of B10 follow a VTF where T0 temperatures of molecular reorientation agree with the Vogel temperatures of shift factor a(T) [61]. This finding indicates that the structural relaxation or the modes of very low index, pertinent to very long-time dynamics of the chain, are not effective over the rotational relaxation, while modes generated by subunits of the chain itself take on relevance.
A rescaling procedure with respect to these relaxation mechanisms may be carried out according to:
τ||(T) ∝ [a (T)]ξ,
and the values of exponents ξ of the power law are reported in Table 4.
It has been demostrated [61,76] that in the IT region the degree of decoupling of the rotational dynamics of cholestane tracer with respect to viscosity should be ascribed in polymers both to the presence of cooperative processes and to steric hindrance effects, related to the polymer connectivity or to the presence of side groups mediating the interaction between tracer diffusion and chain dynamics. Here, a comparison between the decoupling parameter of the rotational relaxation obtained for both copolymers with respect to the respective shift factors could be carried out, since steric hindrance of both copolymers refer to the presence of blocks of same co-units.
The ξ values of fast and slow component for B10 and B20 diblock copolymers result comparable and slighlty diminishing as the percentage of MA4 units increases. Thermoreologically simple random copolymers of same co-units were previously investigated [61]. With respect to diblock copolymers, their fast sites in IT regions exhibited a similar ξ dependence on MA4 percentage; in that case, however, a greater coupling of fast dynamics was found with respect to the slow one. On the other hand, diblock copolymers show a comparable coupling over the two time scales of molecular relaxation. Accordingly to the discussion regarding their activation energies, also this outcome could be interpreted as a marker of tendency to form the ordered supramolecular structures proper of the block copolymers.
Referring to the blends, the VTF parameters characterizing their dynamic response in the proper intervals of temperatures are also reported in Table 4. For slow sites, the VLF regime, set at temperatures higher than the crossover at TgPMMA, exhibits the Vogel temperature T0 in the range of values of PMMA neat samples, either suggested as a trend by ESR literature study on PMMA samples on lower masses or obtained by viscosity measurements [54,76], and found at around 285 K. This provides a nice support to the discussion of Figure 7 regarding the coupling of the slow relaxation of blends to α relaxation of the neat PMMA main chain.
It has already been noted that fast relaxation of blends only shows a unique dynamic trend without any dynamic anomaly. It is describable as a VTF behaviour, that starts above the TNI of PMA4 co-units, as detected in the neat diblock copolymers, then passes smoothly through the TgPMMA and extends up to about 430K, indicating that on this fast timescale the rotational correlation tracks segmental relaxation modes not yet frozen below TgPMMA. Vogel temperature T0 in Table 4 allows to relate relaxation of fast sites to relaxation driven by large subunits of PMMA (as indicated by the T0 value of the fast collective relaxation), but neverthless strongly connected to the presence of a LC block, aiming to acquire an ordered texture at TNI, as suggested by the ideal merging of slow and fast dynamics just at T NI (Figure 6).
With this respect, it has to be noted that ESR investigations have already manifested the ability to detect similar peculiarities of the dynamics, manifesting at nanometer lenght-scale and on a time-scale where local heterogeneity, concentration and self-concentration fluctuations interplay, as a consequence of the polymer architecture or its dynamics. In fact, a study carried out on a random copolymer of MMA-MA4 (40% MA4) co-units revealed the presence of a TNI temperature of the polymer, after extrapolating the fast sites curve, although the nematic-isotropic phase was not detected macroscopically [90]. The analysis of this result, together with the results on mesogenic random copolymers composed by the same co-units [61] (and discussions therein) and with the results on B10/B20 diblock copolymers, located the fast sites at the mesogenic groups/blocks of the polymers for an amount dependent on the percentage of MA4 units in the copolymers.
Collecting all this information, a possible identification of site, where these fast relaxation mechanisms in blends are active, is found in the few available regions of MA4, as also corroborated by the tiny amount of fast population.
More dynamic insight might be provided on the overall rotational relaxation in blends by considering a scaling procedure of correlation times with respect to macroscopic relaxation properties. To this aim, due to the lack of viscosity and rheological measurements on the blend samples, a PMMA sample of literature [54] with comparable tacticity and molecular weight to that used as the major component in the blends was considered (referred to as PMMA22R in Table 2).
The virtual coincidence of the pertinent T0 values of VLF trends from ESR (Table 4) and rheology (Table 2) allowed a rescaling procedure and the calculation of the ξ exponent with respect to viscosity according to eq. 4.
For the slow sites, the ξ exponent denotes a poor coupling to the main polymer relaxation. The fractional exponent of slow dynamics of blends compares with the ξ plateau value found in a study on a PMMA series in the IT region [76] and also with the one pertinent to the IT region of the dynamic rotation of the random MA4-MMA copolymer R10, containing only the 10% of MA4 co-units [61]. Both samples exhibited a homogeneous dynamics with only one site found for the probe rotation, so that the present value for ξ would confirm that the dynamic behaviour of slow sites should be mainly related to α relaxation processes present in a neat PMMA polymer and in the amorphous regions of diblock polymers of blend.
As far as the fast dynamics is concerned, greater values are found for ξ exponent. That behaviour parallels the greater coupling exhibited by fast sites in MA4 homopolymers [36], in random copolymers of same MA4-MMA co-units with high liquid cristallinity [61,91] or in a closely related nematic polyacrylate [70].
In agreement with those results [61,91], a further effective indication is obtained on the location in blends of the probe undergoing the fast reorientation, among/at the mesogenic side groups of the diblock counit.
As a final remark, it appears that the adopted rescaling procedure of fast dynamics in blends with respect to VTF behaviour of PMMA [54] provides a consistent interpretative support for dynamics behaviour at the nanometer length-scale and for the nanosecond times of blends.

4. Conclusions

Due to the sensitivity of the ESR spectroscopy, the present study provided a valuable scenario on dynamics of both diblock copolymers and their blends at nanometer and nanosecond scales.
Fast and slow molecular sites with different relative populations over large temperature ranges were detected for the reorientation of the cholestane molecular tracer, as a consequence of the heterogeneous morphology and dynamics of these materials at nanoscale. In particular the persistent presence of fast sites provided a signature of phenomena of microphase separation and/or confinement in submicrometer-/nanometer-domains even at low content of MA4 co-units in both diblock copolymers and their blends, in which the copolymers containing azobenzene LC blocks are the minority component.
The ability of self-assembling in supramolecular structures of diblock copolymers led to almost parallel trends for the temperature dependence of fast and slow correlation times, with a dynamic crossover recalling dynamic crossovers observed in the literature for polymers and glass formers as the onset of cooperative processes, and located at 1.2Tg. The crossover was detected at a temperature about 1.2 TgPMA4, however, in a dynamic interval where also TODT and TgPMMA contribute synergistically.
In blends fast and slow sites of rotational relaxation characteristcs seemed connetted selectively to their different morphological properties. Slow sites temperature behaviour was similar in shape to diblock copolymers, nevertheless the dynamic change was found at TgPMMA, mostly recalling an α-β relaxation splitting driven by PMMA component, as major component of the blends. Fast sites, free from dynamic anomalies in the investigated temperature range, suggested the presence of a merging at TNI, and were related to molecular probes at the LC block of the copolymer component of the blend.
The evaluation of decoupling degrees of the rotational correlation times from the structural relaxation dynamics or from the viscosity provided more insight, shining a light on the mechanisms of relaxation. In particular, the rotational dynamics in block copolymers is driven by and coupled to more local relaxation processes of the copolymer, due to the monomeric friction coefficients of the two blocks and to the thermorheological complexity of the resultant polymer. In blends, the cooperativity was related to properties of the polymer chain of the majority component, that also determined the overall relaxation trend of fast sites dynamics.
Lastly, the analysis of the dynamics signatures and the coupling data provided in all cases a convenient characterization and a location of the sites available for the molecular reorientation.

Author Contributions

Conceptualization, L.A.; methodology, L.A; software, L.A and E.M.; validation, L.A and E.M.; formal analysis, L.A.; investigation, L.A and E.M.; resources, E.M.; data curation, L.A and E.M.; writing—original draft preparation, L.A.; writing—review and editing, L.A and E.M.; visualization, L.A. and E.M.; project administration, L.A and E.M..; funding acquisition, L.A and E.M. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in the present article.

Acknowledgments

The authors acknowledge Prof. Giancarlo Galli and Prof. Marco Giordano for valuable help and discussions. L.A. acknowledges Dott. Ciro Autiero for help in ESR measurements.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Abetz, V. Preface. In Block Copolymers II; Abetz, V., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2005; pp. IX–X. ISBN 978-3-540-26902-1. [Google Scholar]
  2. Hamley, I.W. The physics of block copolymers; Oxford University Press: Oxford, New York, 1998; ISBN 978-0-19-850218-0. [Google Scholar]
  3. Bates, F.S.; Fredrickson, G.H. Block Copolymers—Designer Soft Materials. Physics Today 1999, 52, 32–38. [Google Scholar] [CrossRef]
  4. Abetz, V.; Simon, P.F.W. Phase Behaviour and Morphologies of Block Copolymers. In Block Copolymers I; Abetz, V., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2005; pp. 125–212. [Google Scholar] [CrossRef]
  5. Li, M.; Coenjarts, C.A.; ·Ober, C. K. Patternable Block Copolymers. In Block Copolymers II; Abetz, V., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2005; pp. 183–226. [Google Scholar] [CrossRef]
  6. Bates, F.S.; Fredrickson, G.H. Block Copolymer Thermodynamics: Theory and Experiment. Annu. Rev. Phys. Chem. 1990, 41, 525–557. [Google Scholar] [CrossRef] [PubMed]
  7. Hu, X.H.; Xiong, S. Fabrication of Nanodevices Through Block Copolymer Self-Assembly. Front. Nanotechnol. 2022, 4, 762996. [Google Scholar] [CrossRef]
  8. Karayianni, M.; Pispas, S. Block copolymer solution self-assembly: Recent advances, emerging trends, and applications. J Polym Sci. 2021, 59, 1874–1898. [Google Scholar] [CrossRef]
  9. Wang, R.Y.; Park, M. J. Self-Assembly of Block Copolymers with Tailored Functionality: From the Perspective of Intermolecular Interactions. Annu. Rev. Mater. Res. 2020, 50, 521–549. [Google Scholar] [CrossRef]
  10. Feng, H.; Lu, X.; Wang, W.; Kang, N.-G.; Mays, J. ; Block Copolymers: Synthesis, Self-Assembly, and Applications. Polymers 2017, 9, 494–525. [Google Scholar] [CrossRef]
  11. Almdal, K. Recent Developments in Synthesis of Model Block Copolymers using Ionic Polymerization. In Developments in Block Copolymer Science and Technology; Hamley, I.W., Ed.; John Wiley: Chichester, West Sussex, 2004; pp. 31–70. ISBN 0-470-84335-7. [Google Scholar]
  12. Cai-yuan, P.; Chun-yan, H. Syntheses and Characterizations of Block Copolymers Prepared via Controlled Radical Polymerization Methods. In Developments in Block Copolymer Science and Technology; Hamley, I. W., Ed.; John Wiley: Chichester, West Sussex, 2004; pp. 71–126. ISBN 0-470-84335-7. [Google Scholar]
  13. Karayianni, M.; Pispas, S. Block copolymer solution self-assembly: Recent advances, emerging trends, and applications. J. Polym. Sci. 2021, 59, 1874–1898. [Google Scholar] [CrossRef]
  14. Yu, H.; Kobayashi, T.; Yang, H. Liquid-Crystalline Ordering Helps Block Copolymer Self-Assembly. Adv. Mater. 2011, 23, 3337–3344. [Google Scholar] [CrossRef]
  15. Zhao, Y.; He, J. Azobenzene-containing block copolymers: the interplay of light and morphology enables new functions. Soft Matter 2009, 5, 2686–2693. [Google Scholar] [CrossRef]
  16. Yu, H.F.; Kobayashi, T. Photoresponsive Block Copolymers Containing Azobenzenes and Other Chromophores. Molecules 2010, 15, 570–603. [Google Scholar] [CrossRef]
  17. Shishido, A. Rewritable holograms based on azobenzene-containing liquid-crystalline polymers. Polym. J. 2010, 42, 525–533. [Google Scholar] [CrossRef]
  18. Seki, T.; Nagano, S. Light-directed Dynamic Structure Formation and Alignment in Photoresponsive Thin Films. Chem. Lett. 2008, 37, 484–489. [Google Scholar] [CrossRef]
  19. Aoki, K.; Iwata, T.; Nagano, S.; Seki, T. Light-Directed Anisotropic Reorientation of Mesopatterns in Block Copolymer Monolayers. Macromol. Chem. Phys. 2010, 211, 2484–2489. [Google Scholar] [CrossRef]
  20. Yu, H. Photoresponsive liquid crystalline block copolymers: From photonics to nanotechnology. Progress in Polymer Science 2014, 39, 781–815. [Google Scholar] [CrossRef]
  21. Homocianu, M.; Fifere, N.; Airinei, A. Azobenzene: research progress and its reflections in applications. In Azobenzene aspects, applications and research; Watson, L.E., Ed.; Nova Science Publishers: Hauppauge, New York, 2017; pp. 1–27. ISBN 9781536106732. [Google Scholar]
  22. Yager, K. G.; Barrett, C. J. Azobenzene Polymers for Photonic Applications. In Smart light responsive materials: azobenzene containing polymers and liquid crystals; Zhao, Y., Ikeda, T., Eds.; John Wiley: Hoboken, New Jersey, 2009; pp. 1–46. ISBN 978 0 470 17578. [Google Scholar]
  23. Natansohn, A.; Rochon, P. Photoinduced Motions in Azo-Containing Polymers. Chem. Rev. 2002, 102, 4139–4175. [Google Scholar] [CrossRef] [PubMed]
  24. Bieringer, T. Photoaddressable Polymers. In Holographic data storage; Coufal, H.J., Psaltis, D., Sincerbox, G.T., Eds.; Springer: New York, 2000; Volume 76, pp. 209–228. ISBN 978-3-642-53680-9. [Google Scholar]
  25. Hvilsted, S.; Sanchez, C.; Alcala, R. The volume holographic optical storage potential in azobenzene containing polymers. J. Mater. Chem. 2009, 19, 6641–6648. [Google Scholar] [CrossRef]
  26. Patanè, S.; Arena, A.; Allegrini, M.; Andreozzi, L.; Faetti, M.; Giordano, M. Near-field optical writing on azo-polymethacrylate spin-coated films. Optics Communications 2002, 210, 37–41. [Google Scholar] [CrossRef]
  27. Menghetti, S.; Alderighi, M.; Galli, G.; Tantussi, F.; Morandini, M.; Fuso, F.; Allegrini, M. All-optical pulsed writing in azobenzene copolymer films in the sub-millisecond regime. J. Mater. Chem. 2012, 22, 14510–14517. [Google Scholar] [CrossRef]
  28. Tantussi, F.; Menghetti, S.; Caldi, E.; Fuso, F.; Allegrini, M.; Galli, G. Pure optical and reversible optically driven nanowriting of azobenzene block copolymers. Appl. Phys. Lett. 2012, 100, 083103. [Google Scholar] [CrossRef]
  29. Yu, H.; Iyoda, T.; Ikeda, T. Photoinduced Alignment of Nanocylinders by Supramolecular Cooperative Motions. J. Am. Chem. Soc. 2006, 128, 11010–11011. [Google Scholar] [CrossRef]
  30. Robeson, L.M. Polymer Blends a Comprehensive Review; Carl Hanser Verlag: Munich, Germany, 2007; pp. 1–6. ISBN 978-1-56990-408-4. [Google Scholar]
  31. Sionkowska, A. Current research on the blends of natural and synthetic polymers as new biomaterials: Review. Progress in Polymer Science 2011, 36, 1254–1276. [Google Scholar] [CrossRef]
  32. Utracki, L.A. , P., Gupta, R.K. Polymer Blends: Introduction. In Polymer Blends Handbook, 2nd ed.; Utracki, L., Wilkie, C., Eds.; Springer: Dordrecht, Netherlands, 2014; pp. 3–170. [Google Scholar] [CrossRef]
  33. Breiner, T.; Kreger, K.; Hagen, R.; Häckel, M.; Kador, L.; Müller, A.H.E.; Kramer, E.J.; Schmidt, H.W. Blends of Poly(methacrylate) Block Copolymers with Photoaddressable Segments. Macromolecules 2007, 40, 2100–2108. [Google Scholar] [CrossRef]
  34. Forcén, P.; Oriol, L.; Sánchez, C.; Rodríguez, F.J.; Alcalá, R.; Hvilsted, S.; Jankova, K. Volume holographic storage and multiplexing in blends of PMMA and a block methacrylic azopolymer, using 488 nm light pulses in the range of 100 ms to 1 s. European Polymer Journal 2008, 44, 72–78. [Google Scholar] [CrossRef]
  35. Andreozzi, L.; Faetti, M.; Galli, G.; Giordano, M.; Palazzuoli, D. Nanoscale Heterogeneities in Nematic Azobenzene Polymethacrylates for Optical Nanowriting. Macromol. Symp. 2004, 218, 323–332. [Google Scholar] [CrossRef]
  36. Andreozzi, L.; Faetti, M.; Galli, G.; Giordano, M.; Palazzuoli, D. An ESR Study on the Heterogeneity of Dynamics in a Nematic Polymer Induced by Thermal Annealing in the Isotropic Melt. Macromolecules 2001, 34, 7325–7330. [Google Scholar] [CrossRef]
  37. Assenheim, H.M. Introduction to Electron Spin Resonance; Springer: Berlin Heidelberg, 1966; pp. 140–162. ISBN 978-1-4899-5504-3. [Google Scholar]
  38. Weil, J.A.; Bolton, J.R. Electron paramagnetic resonance spectroscopy Elementary Theory and Practical Applications, 2nd ed.; John Wiley & Sons: Hoboken, New Jersey, 2007; pp. 414–421. ISBN 978-0471-75496-1. [Google Scholar]
  39. Bercu, V.; Massa, C.A.; Pizzanelli, S.; Pardi, L. , Leporini, D.; Martinelli, M. Glassforming Liquids, Amorphous and Semicrystalline Polymers: Exploring their Energy Landscape and Dynamical Heterogeneity by Multi-frequency High-Field EPR. Appl. Magn. Reson. 2020, 51, 1591–1605. [Google Scholar] [CrossRef]
  40. Pitt, C.G.; Wang, J.; Shah, S.S.; Sik, R.; Chignell, C.F. ESR spectroscopy as a probe of the morphology of hydrogels and polymer-polymer blends. Macromolecules 1993, 26, 2159–2164. [Google Scholar] [CrossRef]
  41. Uddin, M.A.; Yu, H.; Wang, L.; Naveed, K.R.; Haq, F.; Amin, B. U.; Mehmood, S.; Nazir, A.; Xing, Y.; Shen, D. Recent progress in EPR study of spin labeled polymers and spin probed polymer systems. Journal of Polymer Science 2020, 58, 1924–1948. [Google Scholar] [CrossRef]
  42. Veksli, Z.; Andreis, M.; Rakvin, B. ESR spectroscopy for the study of polymer heterogeneity. Progress in Polymer Science 2000, 25, 949–986. [Google Scholar] [CrossRef]
  43. Valić, S.; Andreis, M.; Klepac, D. ESR Spectroscopy of Multiphase Polymer Systems. In Handbook of Multiphase Polymer Systems, 1st ed.; Boudenne, A., Ibos, L., Candau, Y., Thomas, S., Eds.; John Wiley & Sons, 2011; pp. 551–584. ISBN 978-0-470-71420-1. [Google Scholar]
  44. Freed, H.J. Theory of Slow Tumbling ESR Spectra for Nitroxides. In Spin Labeling: Theory and Application I; Berliner, L.J., Ed.; Academic Press: New York, 1976; pp. 53–132. ISBN 0-12-092350-5. [Google Scholar]
  45. Miller, W.G. Spin-Labeled Synthetic Polymers. In Spin Labelling II: Theory and Applications; Berliner, L.J., Ed.; Academic Press: New York, 1976; pp. 173–221. ISBN 0-12-092352-1. [Google Scholar]
  46. Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F.; Galli, G. Heterogeneities in the Dynamics of a Molecular Tracer in Mesogenic and Nonmesogenic Azobenzene Copolymers. Mol. Cryst. Liq. Cryst. 2006, 450, 363–371. [Google Scholar] [CrossRef]
  47. Faetti, M.; Giordano, M.; Leporini, D.; Pardi, L. Scaling Analysis and Distribution of the Rotational Correlation Times of a Tracer in Rubbery and Glassy Poly(vinyl acetate): An Electron Spin Resonance Investigation. Macromolecules 1999, 32, 1876–1882. [Google Scholar] [CrossRef]
  48. Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F. Dynamic crossovers and activated regimes in a narrow distribution poly(n-butyl acrylate): an ESR study. J. Phys.: Condens. Matter 2006, 18, 6481–6492. [Google Scholar] [CrossRef] [PubMed]
  49. Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F. J. J. Non-Cryst. Solids 2006, 352, 5050–5054. [CrossRef]
  50. Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F. Probing the cooperative dynamics varying the side-chain length of poly(alkyl acrylate)s: ESR experiments. Philosophical Magazine 2007, 87, 799–810. [Google Scholar] [CrossRef]
  51. Andreozzi, L.; Faetti, M.; Giordano, M.; Zulli, F. Length Scales and Dynamics in the Reorientational Relaxation of Tracers in Molecular and Polymeric Glass Formers via Electron Spin Resonance Spectroscopy. J. Phys. Chem. B 2010, 114, 12833–12839. [Google Scholar] [CrossRef]
  52. Bartoš, J.; Andreozzi, L.; Faetti, M.; Šauša, O.; Račko, D.; Krištiak, J. Free volume in poly(propylene glycol) and its relationships to spin probe reorientation. J. Non-Cryst. Solids 2006, 352, 4785–4789. [Google Scholar] [CrossRef]
  53. Angeloni, A.S.; Caretti, D.; Laus, M.; Chiellini, E.; Galli, G. Mesomorphic Polyacrylates Containing Isomeric Methyl-Substituted Azobenzene Mesogens. J. Polym. Sci., Part A: Polym. Chem. 1991, 29, 1865–1873. [Google Scholar] [CrossRef]
  54. Fuchs, K.; Friedrich, C.; Weese, J. Viscoelastic Properties of Narrow-Distribution Poly(methyl methacrylates). Macromolecules 1996, 29, 5893–5910. [Google Scholar] [CrossRef]
  55. Andreozzi, L.; Galli, G.; Giordano, M.; Zulli, F. A Rheological Investigation of Entanglement in Side-Chain Liquid-Crystalline Azobenzene Polymethacrylates. Macromolecules 2013, 46, 5003–5017. [Google Scholar] [CrossRef]
  56. Wunderlich, B. The nature of the glass transition and its determination by thermal analysis. In Assignment of the Glass Transition; Seyler, R.J., Ed.; Am. Soc. Testing and Materials: West Conshohocken, PA, 1994; pp. 17–31. ISBN -13. [Google Scholar]
  57. Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; Taylor & Francis: Boca Raton, FL, 2007; ISBN 978-1-57444-779-8. [Google Scholar]
  58. Lim, C.K.; Cohen, R.E.; Tschoegl, N.W. Time-temperature superposition in block copolymers. In Multicomponent Polymer Systems; Platzer, N.A.J., Ed.; American Chemical Society: Washington, DC, 1971; pp. 397–417. ISBN 978-0-8412-0113-2. [Google Scholar] [CrossRef]
  59. Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F.; Galli, G.; Menghetti, S. Linear Viscoelastic Behavior of an Azobenzene Nematic Block Copolymer. Mol. Cryst. Liq. Cryst. 2011, 549, 133–139. [Google Scholar] [CrossRef]
  60. Leuzzi, L.; Nieuwenhuizen, T.M. Thermodynamics of the Glassy State; Taylor & Francis: Boca Raton, FL, 2008; pp. 23–26. ISBN 978-0-7503-0997-4. [Google Scholar]
  61. Andreozzi, L.; Galli, G.; Giordano, M.; Martinelli, E.; Zulli, F. Heterogeneity and Dynamics in Azobenzene Methacrylate Random and Block Copolymers: A Nanometer–Nanosecond Study by Electron Spin Resonance Spectroscopy. Macromolecules 2015, 48, 6541–6552. [Google Scholar] [CrossRef]
  62. Honerkamp, J.; Weese, J. A nonlinear regularization method for the calculation of relaxation spectra. Rheol. Acta 1993, 32, 57–64. [Google Scholar] [CrossRef]
  63. Smith, I.C.P.; Burler, K. W. Oriented Lipid Systems as Model Membranes. In Spin Labeling: Theory and Application I; Berliner, L.J., Ed.; Academic Press: New York, 1976; ISBN 0-12-092350-5. [Google Scholar]
  64. Carr, S.G.; Kao, S.K.; Luckhurst, G.R.; Zannoni, C. On the Ordering Matrix for the Spin Probe (3-spiro [2′- N- oxyl-3′,3′-dimethyloxazolidine])-5α-cholestane, in the Nematic Mesophase of 4,4′-dimethoxyazoxybenzene. Mol. Cryst. Liq. Cryst. 1976, 35, 7–13. [Google Scholar] [CrossRef]
  65. Andreozzi, L.; Di Schino, A.; Giordano, M.; Leporini, D. Evidence of a fractional Debye-Stokes-Einstein law in supercooled o-terphenyl. Europhys. Lett. 1997, 38, 669–674. [Google Scholar] [CrossRef]
  66. Likhtenshtein, G.I. Nitroxide Spin Probes for Studies of Molecular Dynamics and Microstructure. In Nitric Oxide Donors: For Pharmaceutical and Biological Applications; Wang, P.G., Cai, T.B., Taniguchi, N., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, 2005; pp. 205–232. ISBN 978-3-527-31015-9. [Google Scholar]
  67. Beiner, M.; Huth, H.; Schroter, K. Crossover region of dynamic glass transition: general trends and individual aspects. J. Non-Cryst. Solids 2001, 279, 126–135. [Google Scholar] [CrossRef]
  68. Khodadadi, S.; Sokolov, A.P. Protein dynamics: from rattling in a cage to structural relaxation. Soft Matter 2015, 11, 4984–4998. [Google Scholar] [CrossRef]
  69. Andreozzi, L.; Giordano, M.; Leporini, D. Efficient characterizationof the orientational ordering of ESR-active probes in supermolecular fluids. Appl. Magn. Reson. 1993, 4, 279–295. [Google Scholar] [CrossRef]
  70. Andreozzi, L.; Giordano, M.; Leporini, D. Electron Spin Resonance in polymeric liquid crystals. In Structure and Transport Properties in Organized Materials; Chiellini, E., Giordano, M., Leporini, D., Eds.; World Scientific: Singapore, 1997; pp. 207–242. ISBN 981-02-1894-X. [Google Scholar]
  71. Perrin, J. Mouvement brownien d'un ellipsoide - I. Dispersion diélectrique pour des molécules ellipsoidales. J. Phys. Radium 1934, 5, 497–511. [Google Scholar] [CrossRef]
  72. Favro, L.D. Theory of the Rotational Brownian Motion of a Free Rigid Body. Phys. Rev. 1960, 119, 53–62. [Google Scholar] [CrossRef]
  73. Polnaszek, C. F.; Marsh, D.; Smith, I. C. P. Simulation of the EPR spectra of the cholestane spin probe under conditions of slow axial rotation. Application to gel phase dipalmitoyl phosphatidyl choline. J. Magn. Reson. 1981, 43, 54–64. [Google Scholar] [CrossRef]
  74. Robinson, G.H.; Dalton, L.R. Approximate Methods for the Fast Computation of EPR and ST-EPR Spectra. V. Application of the Perturbation Approach to the Problem of Anisotropic Motion. Chem. Phys. 1981, 54, 253–259. [Google Scholar] [CrossRef]
  75. Nordio, P.L. General Magnetic Resonance Theory. In Spin Labeling: Theory and Application I; Berliner, L.J., Ed.; Academic Press: New York, 1976; pp. 5–52. ISBN 0-12-092350-5. [Google Scholar]
  76. Zulli, F.; Giordano, M.; Andreozzi, L. Chain-Length Dependence of Relaxation and Dynamics in Poly(methyl methacrylate) from Oligomers to Polymers. Macromolecules 2018, 51, 1798–1810. [Google Scholar] [CrossRef]
  77. Siderer, Y.; Luz, Z. Analytical Expressions for Magnetic Resonance Lineshapes of Powder Samples. J. Magn. Reson. 1980, 37, 449–463. [Google Scholar] [CrossRef]
  78. Shah, M.; Pryamitsyn, V.; Ganesan, V. A Model for Self-Assembly in Side Chain Liquid Crystalline Block Copolymers. Macromolecules 2008, 41, 218–229. [Google Scholar] [CrossRef]
  79. Andreozzi, L.; Giordano, M.; Faetti, M.; Palazzuoli, D. On the Simulation of Inhomogeneous ESR Lineshape of a Spin Probe in a Liquid Crystalline Polymer. Appl. Magn. Reson. 2002, 22, 71–87. [Google Scholar] [CrossRef]
  80. Donth, E. J. The Glass Transition:Relaxation Dynamics in Liquids and Disordered Materials, 1st ed.; Springer: Berlin, Heidelberg, Germany, 2001; pp. 11–225. [Google Scholar] [CrossRef]
  81. Wunderlich, W. Physical Constants of Poly(methylmethacrylate). In Polymer handbook, 4th ed.; Brandrup, J., Immergut, E.H., Grulke, E.A., Eds.; Wiley: New York, 1999; pp. 87–90. ISBN 0-471-16628-6. [Google Scholar]
  82. McCrum, N.G.; Read, B.E.; Williams, G. Anelastic and Dielectric Effects in Polymeric Solids; Dover Publications: New York, 1991; ISBN 978-0486667522. [Google Scholar]
  83. Hayakawa,T. ; Adachi, K. Dielectric Relaxation of Poly(n-butyl acrylate). Polym. J. 2000, 32, 845–848. [Google Scholar] [CrossRef]
  84. Andreozzi, L.; Faetti, M.; Giordano, M.; Leporini, D. Scaling of the Rotational Relaxation of Tracers in O-Terphenyl: A Linear and Nonlinear ESR Study. J. Phys. Chem. B 1999, 103, 4097–4103. [Google Scholar] [CrossRef]
  85. Andreozzi, L.; Bagnoli, M.; Faetti, M.; Giordano, M. Jump Rotation in a Molecular Glass Former. Philos. Mag. B 2002, 82, 409–419. [Google Scholar] [CrossRef]
  86. Andreozzi, L.; Di Schino, A.; Giordano, M.; Leporini, D. A study of the Debye -Stokes -Einstein Law in Supercooled Fluids. J. Phys.:Condens. Matter 1996, 8, 9605–9608. [Google Scholar] [CrossRef]
  87. Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F.; Szanka, I.; Galli, G. On the Dynamics of the Cholestane Spin Probe in a Nematic Azobenzene Side Group Oligomer. Mol. Cryst. Liq. Cryst. 2007, 465, 25–35. [Google Scholar] [CrossRef]
  88. Shiotani, M.; Sohma, J. ESR Studies of Molecular Motion of Spin Labelled Poly(methyl methacrylate). Polymer Journal 1977, 9, 283–291. [Google Scholar] [CrossRef]
  89. Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: New York, 2011; pp. 754–758. ISBN 978-1-4419-7648-2. [Google Scholar]
  90. Galli, G.; Szanka, I.; Andreozzi, L.; Autiero, C.; Faetti, M.; Giordano, M.; Zulli, F. Nanoscale Heterogeneities in Nematic Azobenzene Polymethacrylates for Optical Nanowriting. Macromol. Symp. 2006, 245-246, 463–469. [Google Scholar] [CrossRef]
  91. Andreozzi, L.; Faetti, M.; Giordano, M.; Palazzuoli, D.; Galli, G. Heterogeneity in the dynamics of a molecular tracer dissolved in liquid crystal homopolymer and copolymer. Mol. Cryst. Liq. Cryst. 2004, 411, 515–523. [Google Scholar] [CrossRef]
Preprints 85426 g001
Figure 1. Diblock copolymer structure. Bx (x=20, 10 mol%, y=100–x).
Figure 1. Diblock copolymer structure. Bx (x=20, 10 mol%, y=100–x).
Preprints 85426 g001
Preprints 85426 g002
Figure 2. Structure of the cholestane molecular tracer.
Figure 2. Structure of the cholestane molecular tracer.
Preprints 85426 g002
Preprints 85426 g003
Figure 3. (a) ESR lineshape of B10 at the start and the end of annealing at Ta = 387 K [61]. (b) ESR lineshape of b5B10 at the start and the end of annealing at Ta = 400 K.
Figure 3. (a) ESR lineshape of B10 at the start and the end of annealing at Ta = 387 K [61]. (b) ESR lineshape of b5B10 at the start and the end of annealing at Ta = 400 K.
Preprints 85426 g003
Preprints 85426 g004
Figure 4. Comparison of ESR lineshapes of B20, B10 diblock copolymers and blends recorded at the same temperature T = 415K.
Figure 4. Comparison of ESR lineshapes of B20, B10 diblock copolymers and blends recorded at the same temperature T = 415K.
Preprints 85426 g004
Preprints 85426 g005
Figure 5. Temperature dependence of fast and slow rotational correlation times in B20 and B10 copolymers [61].
Figure 5. Temperature dependence of fast and slow rotational correlation times in B20 and B10 copolymers [61].
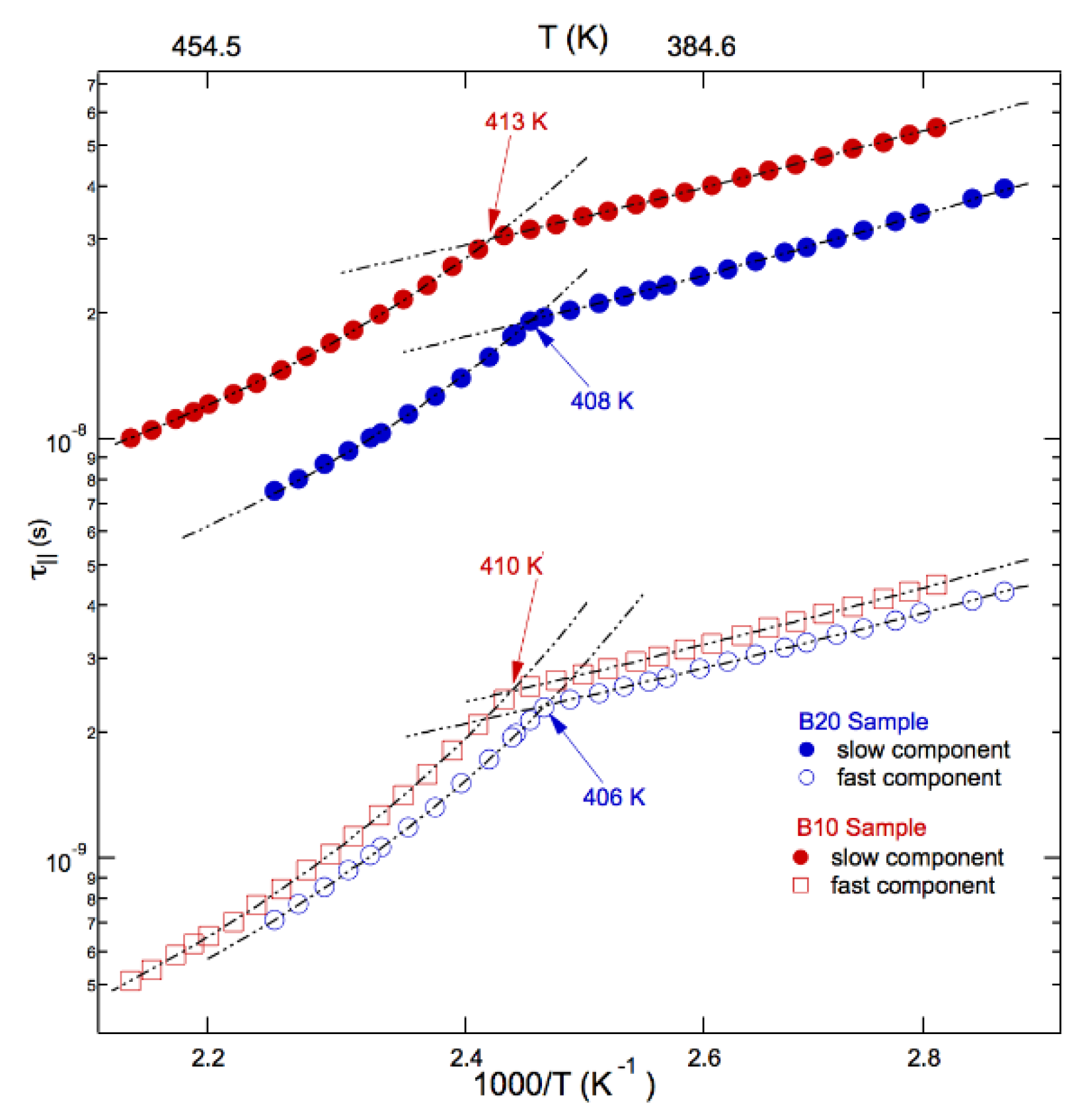
Preprints 85426 g005
Preprints 85426 g006
Figure 6. Arrhenius plot of rotational correlation times in blends.
Figure 6. Arrhenius plot of rotational correlation times in blends.
Preprints 85426 g006
Preprints 85426 g007
Figure 7. Comparison of the temperature dependence of slow rotational correlation times in B10, B20 and blend. In figure the temperature dependence of rotational correlation times in PMMA4900 [76] are also reported.
Figure 7. Comparison of the temperature dependence of slow rotational correlation times in B10, B20 and blend. In figure the temperature dependence of rotational correlation times in PMMA4900 [76] are also reported.
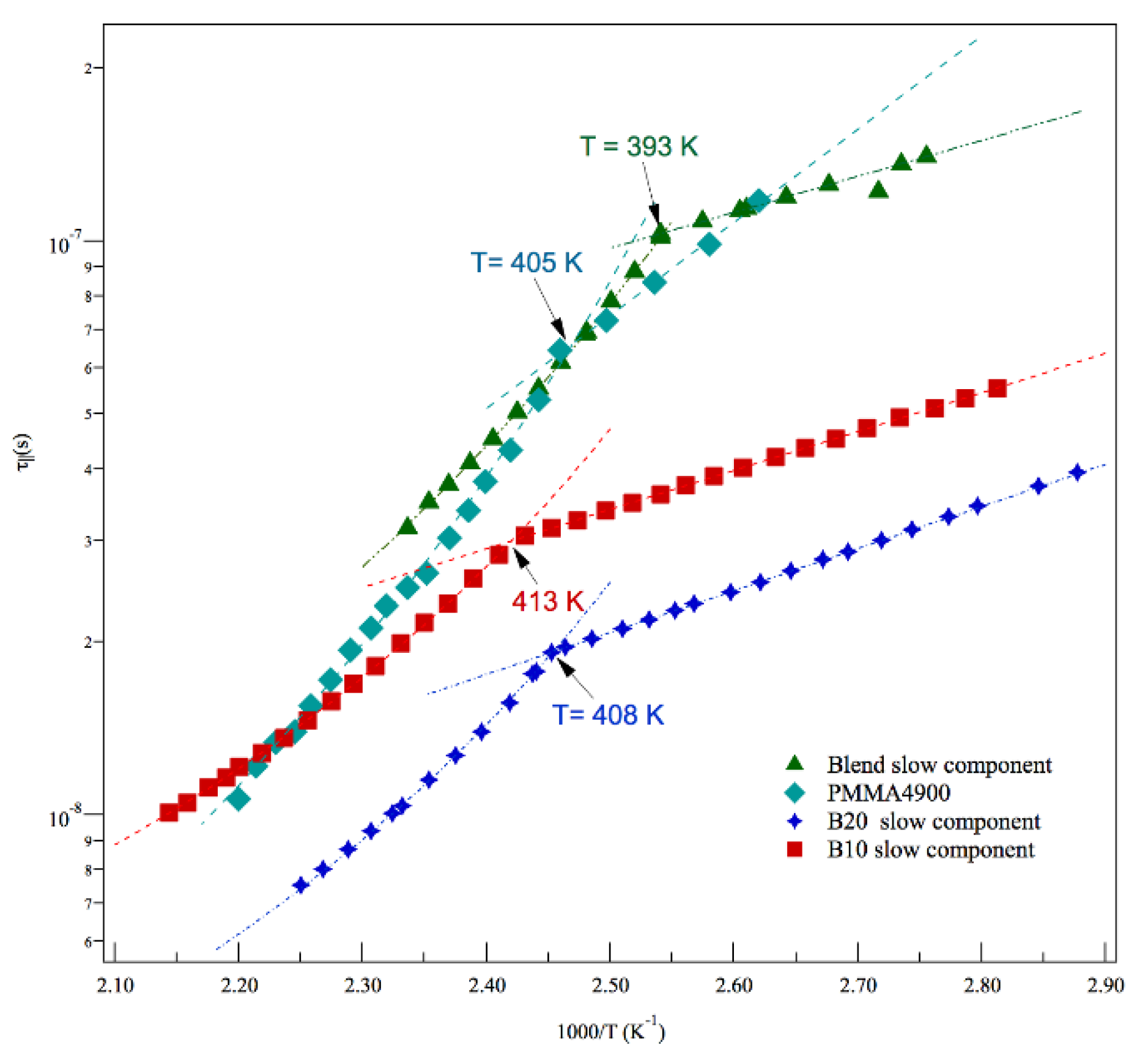
Preprints 85426 g007
Preprints 85426 g008
Figure 8. Population of fast dynamic component in B10 [61].
Figure 8. Population of fast dynamic component in B10 [61].
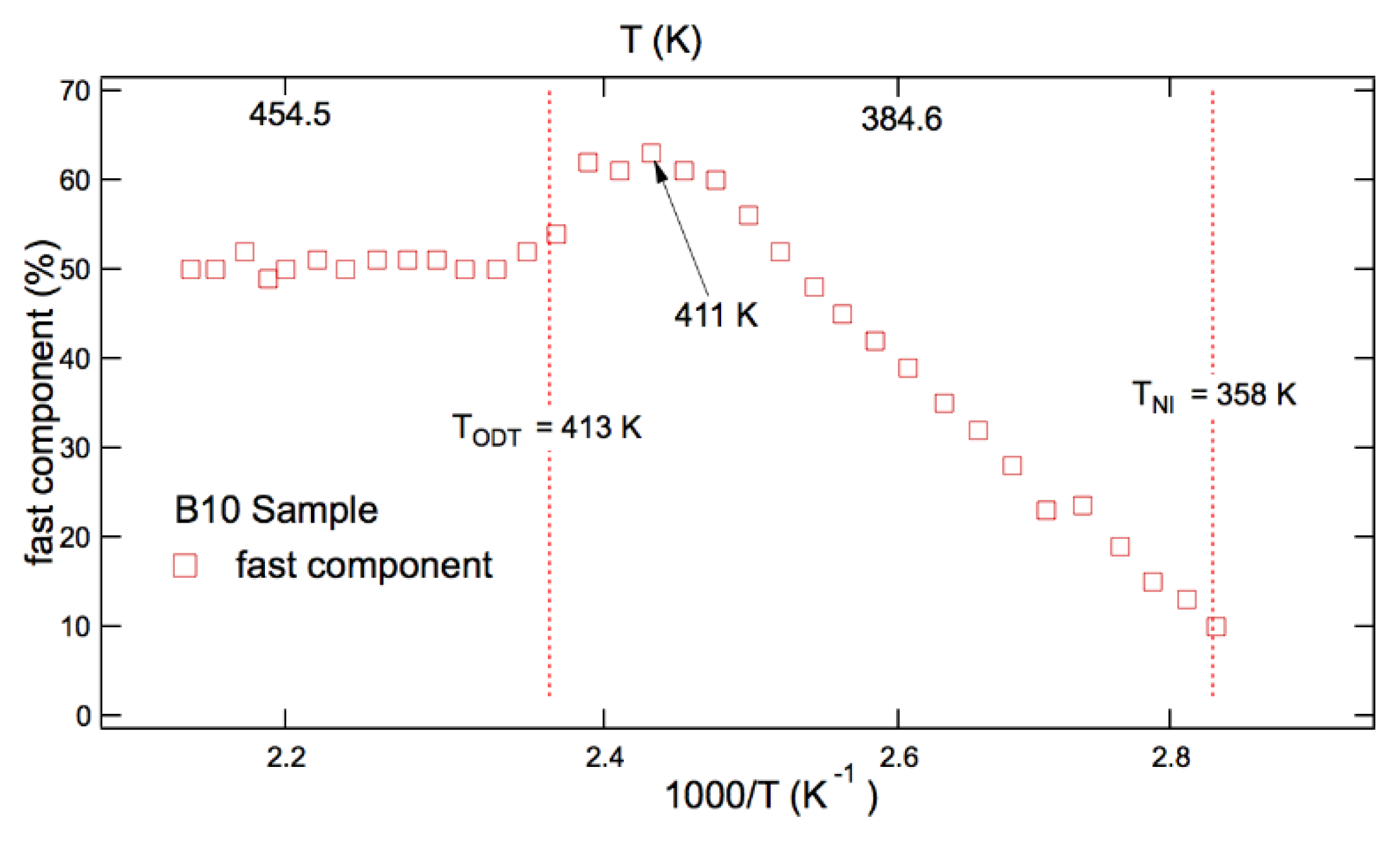
Preprints 85426 g008
Table 1. Chemical and Physical Characterization of the Copolymers and Blends.
Table 1. Chemical and Physical Characterization of the Copolymers and Blends.
Sample x
(mol%)		 Mn
(kg mol–1)		 Mw/Mn TgPMA4
(K)		 TgPMMA
(K)		 TNI
(K)		 TODT
(K)
PMMA 0 21 1.27 --- 385 --- ---
B20 20 34 1.31 324 394 358 413
B10 10 27 1.27 328 397 353 423
PMA4 100 29.9 2.43 305 --- 357 ---
PMMA22R1 0 24 1.04 --- 392 --- ---
1Data of sample PMMA22R are reported from literature [54]. PMMA22R presents the same standard microstructure as the PMMA polymer of this work.
Table 2. VFT Parameters of B20 and B10 copolymers.
Table 2. VFT Parameters of B20 and B10 copolymers.
Sample Variable η ∞ (Pa s) Tb (K) T0 (K)
B20 η (T) (3.00±0.05)102 210±30 330±30
a(T) - 1450±50 340±4
B10 η (T) (7.24±0.05)10-2 1800±250 240±20
a(T) - 1950±50 323±3
PMMA22R 1 η (T) - 3530±50 286±3
1Data of PMMA22R sample from literature [54].
Table 3. Values of the magnetic tensor components in the molecular frame.
Table 3. Values of the magnetic tensor components in the molecular frame.
Samples gxx gyy gzz axx (gauss) ayy (gauss) azz (gauss)
PMMA49001 2.0026 2.0093 2.0066 32.3 6.0 5.0
HomoPMA42 2.0026 2.0092 2.0069 32.6 5.5 5.0
B203, B10 3 2.0026 2.0092 2.0069 32.9 5.5 5.0
Blends 2.0026 2.0092 2.0069 32.9 5.5 5.0
Data from: 1 [76], 2 [36], 3 [61].
Table 4. Dynamics details and parameters of the block copolymers and blends.
Table 4. Dynamics details and parameters of the block copolymers and blends.
Sample T range (K) T region1 Law2 τ||∞ (s) T0 (K) Tb (K) ξ3 ΔE (kJ mol–1)
B20 445–406 IT(F) VFT (2.5±0.2)x10−11 340±7 200±20 0.14±0.01 ---
406–347 LT(F) Arr (5.5±0.2)x10−11 --- --- --- 14±1
445–408 IT(S) VFT (4.7±0.2)x10−10 340±7 180±25 0.12±0.02 ---
408–347 LT(S) Arr (3.1±0.2)x10−10 --- --- --- 15±1
B10 467–410 IT(F) VFT (2.2±0.2)x10−11 323±7 350±30 0.18±0.02 ---
410–357 LT(F) Arr (5.5±0.2)x10−11 --- --- --- 13±1
467–413 IT(S) VFT (9.8±0.2)x10−10 323±7 260±25 0.13±0.01 ---
413–357 LT(S) Arr (2.4±0.2)x10−8 --- --- --- 13±1
b5B20
and
b5B10		 428-363 (F) VFT (4.3±0.3)x10−12 276±5 795±20 0.23c±0.01 ---
428-393 IT(S) VFT (6.0±0.2)x10−10 276±6 604±20 0.17c±0.01 ---
393-363 LT(S) Arr (2.6±0.2)x10−9 --- --- --- 12±1
1 Key: intermediate-temperature (IT); low-temperature (LT) region. Slow (S) or fast (F) dynamic component is also specified. 2 Arrhenius or VFT (equation 2) behavior. 3 The ξ coefficient for blends was calculated with respect to Tb value of literature PMMA of comparable molar mass (sample PMMA22R in [54]).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
An ESR Study Comparing Nanometer-Nanosecond Dynamics in Diblock Copolymers and Their PMMA Binary Blends

Laura Andreozzi

et al.

,

2023

Thermodynamic and Dynamic Transitions and Interaction Aspects in Reorientation Dynamics of Molecular Probe in Organic Compounds: A Series 1-Alkanols with TEMPO

Josef Bartoš

et al.

,

2023

Rotation Dynamics of Star Block Copolymers under Shear Flow

Diego Jaramillo-Cano

et al.

,

2018

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated