Prerpints.org logo
Preprint
Article

An Optimal Switching Sequence Model Predictive Control Scheme for the 3L-NPC with Output LC Filter

Altmetrics

Downloads

118

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 December 2023

Posted:

14 December 2023

You are already at the latest version

Alerts
Abstract
In some applications of microgrid and distributed generation, it is required to feed islanded or stand-alone loads with high-quality voltage to provide low total harmonic distortion (THD). To fulfil these demands, an LC filter is connected to the output terminals of power electronics converters. A cascaded voltage and current control loop with pulse-width modulation schemes are used to regulate the voltage and current in these systems. However, these strategies have some drawbacks, particularly when multiple-input multiple-output plants (MIMO) are controlled using single-input single-output (SISO) design methods. This methodology usually produces a sluggish transient response and cross-coupling between different control loops. In this paper, a model predictive control (MPC) strategy based on the concept of optimal switching sequences (OSS) is designed to control voltage and current in an LC filter connected to a three-level neutral-point clamped converter. The strategy solves two well-formulated optimisation problems to achieve control of the LC filter variables and the voltages of the DC-link capacitors. Hardware-in-the-Loop (HIL) results are obtained to validate the feasibility of the proposed strategy, using a PLECS-RT HIL platform and a DSP Microlab Box controller. In addition to the good dynamic performance of the proposed OSS-MPC, it is demonstrated by the HIL results that the control algorithm is capable of obtaining low total harmonic distortion (THD) in the output voltage for different conditions.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

When power converters are utilised to supply electrical energy to islanded loads, in microgrids or distributed generation applications, typically an L C filter is connected at the converter outputs [1,2,3]. For instance, converters augmented by L C filters are used in applications such as uninterruptible power supplies (UPS) [4], energy storage systems [5], motor drives [6], microgrids [7], etc.
When SISO control tools are utilised, to design the control systems of power converters equipped with L C filters, typically two cascaded PI or PR control loops are required: an outer voltage control loop, and an inner current control loop [3,8]. The voltage loop computes the reference for the inner current loop, and the current loop computes the desired converter voltage to be synthesized by a pulse-width modulation (PWM) scheme. However, as discussed in [7], the cascaded interconnection of the voltage and current control loops has some drawbacks. First, because SISO design tools are used, the inner and outer loops are separately designed with different bandwidths to avoid cross-couplings between the dynamics of the voltage and current control loops (usually, the outer loop is one order of magnitude slower than the inner loop). This produces a relatively slower transient response. Second, the controllers must be carefully tuned because their parameters affect the system’s stability. To overcome the drawbacks of cascaded linear controllers, model predictive control schemes, which are MIMO systems have been recently proposed.
Model Predictive Control (MPC) has been garnering growing interest in the realm of power electronics converter applications. Most common applications include grid-connected converters, inverters with RL load, inverters with output LC filter, and high-performance drives [9]. MPC has several advantages such as simplicity for the inclusion of nonlinearities, simple treatment of constraints, the multivariable case can be easily considered, dead times can be compensated, etc [10]. On the other hand, the disadvantage of MPC is its relatively high computational load, particularly in power converter topologies where a large number of vectors are available. However, the exponential development in the processing power of microprocessors (such as digital signal processors and field-programmable gate arrays) has allowed the implementation of MPC algorithms in real-time platforms [11].
A wide variety of MPC algorithms for power electronics converters exist. An MPC algorithm can be considered, in general terms, as any algorithm that uses a model of the system to predict its future behaviour and select the most appropriate control action based on the solution to an optimal criterion [12]. The optimal criterion is evaluated in a cost function and can be, for example, tracking of the system state variables, minimising common-mode voltage, or reducing the converter switching frequency [12,13]. After the optimal criterion has been reached, and consequently the best possible solution to the optimisation problem has been obtained, the algorithm sends it to the converter to be synthesised.
MPC algorithms are classified according to the nature of the optimisation variable in the control problem. In broad terms, these algorithms for power electronics are classified as Direct MPC or Indirect MPC methods [13]. In direct MPC methods, the optimisation variable is an integer-valued vector representing the state of the converter switching devices. Conversely, in indirect MPC the optimisation variable is a real-valued vector representing the fundamental component of the converter output voltage or duty cycles.
Direct MPC methods are subdivided into three categories: optimal switching vector MPC (OSV-MPC), MPC with hysteresis bounds, and MPC with an implicit modulator. OSV-MPC, commonly named as Finite Control Set MPC (FCS-MPC) in the literature, was firstly proposed to control the output current of a two-level inverter connected to an RL load [14]. Since then, it has been applied to many converter topologies [9]. In this strategy, the converter switches are directly computed and sent to the converter. Thus, allowing direct manipulation of the controlled variables. The advantages of OSV-MPC are an intuitive design procedure, straightforward implementation and fast transient response [13]. However, they come at the cost of high computational complexity, particularly for multilevel power converters, and variable switching frequency due to the absence of a modulator [15].
Direct MPC methods with implicit modulator have been proposed to overcome the issue of variable switching frequency introduced by OSV-MPC while maintaining its advantages [16,17]. These strategies attempt to emulate the behaviour of pulse-width modulation techniques. In particular, Optimal Switching Sequence MPC (OSS-MPC) and Modulated MPC (M2PC) introduce the concept of variable switching time instants [13]. According to the concept of variable switching time instants, the position of the converter switches can change at any moment during a sampling interval. Then, the strategies compute a sequence of switch positions and their corresponding duty cycles to be applied during the next sampling interval. Thus, a fixed switching frequency is achieved resulting in a reduction of harmonic distortion [13]. However, M2PC is prone to suboptimality because the optimisation problem is solved in two stages: the first stage is to find the optimal switch positions and the second stage is to compute the duty cycles [18].
OSS-MPC avoid suboptimal solutions by computing the optimal sequence of switch positions and their corresponding duty cycles in one stage. The strategy was first introduced for power control of a grid-connected two-level inverter [17]. Then, the strategy was modified to be used in other converter topologies such as a three-level neutral-point-clamped (3L-NPC) inverter and vienna rectifier [19,20,21,22]. In [23], OSS-MPC was used for voltage control of an LC-filtered two-level inverter achieving low output voltage ripple and reduced harmonic content compared against other MPC methods (such as OSV-MPC). In this paper, the OSS-MPC presented in [22] is extended to three-level neutral-point-clamped (3L-NPC) inverters with output LC filter in standalone operation (such as UPS). The strategy uses a prediction model based on the improved Euler method to compute the future value of the load output voltage and inductor filter current. The predicted values are compared against the desired reference values in the cost function of an optimisation problem. The cost function penalizes the deviation between the measured values and the reference values, and also the control effort of the converter. The optimisation problem is solved offline to compute an optimal switching sequence to be applied by the converter. The optimal switching sequence is then transformed into a three-phase reference signal which is used in an optimisation problem to compute an optimal common-mode voltage to balance the DC-link capacitors of the converter. The common-mode voltage is then added to the three-phase reference signal and the resulting optimal three-phase reference is sent to an In-Phase Disposition PWM scheme to generate the pulses of the switching devices.

2. The 3L-NPC Inverter

The 3L-NPC was the first multilevel converter topology, proposed by the group of Akagi in [24]. It was introduced around 1980 to reduce the pulsating torque and harmonic losses on AC drives; thus, improving the efficiency and reducing the cost of the system. Nowadays, this converter topology is the standard for medium and high-voltage applications [25,26]. In the mining industry, for example, 3L-NPC converters are used in variable frequency drives (VFD) for long belt-conveyor systems carrying ore [27].
As shown in the circuit diagram in Figure 1(a), the 3L-NPC converter is composed of four switches and two clamped diodes per leg, producing a total of 27 three-phase switching states u abc for the whole converter, where u abc ∈ U ≜ { − 1 , 0 , 1 } 3 . As depicted in Figure 1(b), these switching states produce 19 non-redundant and 8 redundant switching vectors (SVs) u s in the α β frame, where u s = T α β u abc , and T α β is the amplitude invariant a b c -to- α β transformation [28].
According to the circuit diagram depicted in Figure 1(a), the inverter voltages v abc = v ao v bo v co ⊺ are given by
v abc = 1 2 V dc u abc + ( 1 − | u abc | ) v n
where | u abc | = | u a | | u b | | u c | ⊺ , and v n = 1 2 ( v C 2 − v C 1 ) is the NP-voltage. Using the transformation T α β , the inverter voltages (1) in the stationary α β frame can be expressed as:
v s = 1 2 V dc u s − T α β | u abc | v n .
On the other hand, for a three-phase load with a floating neutral, the NP-voltage evolves as a function of the NP-current i n according to:
( C 1 + C 2 ) d v n d t = i n , i n = | u abc | ⊺ i abc
Therefore, for a given output current i abc = i s a i s b i s c ⊺ , as shown in (3), only small- and medium-size SVs, u S and u M in fig:NPC1](b) respectively, can affect the NP-voltage [29]. However, to balance the NP voltage, small SVs play a significant role because the redundancy of each SV drives an NP-current of the same amplitude but in the opposite direction. This tendency impacts v n but not v s when the capacitors are balanced with a negligible voltage ripple, i.e., v n ≈ 0 .
To synthesize a desired inverter output voltage, the three nearest SVs are typically employed in carrier-based and space vector PWM techniques [29,30]. Due to the presence of redundancies, several switching sequences (or switching patterns) can synthesize the desired output voltage. Therefore, the generation of switching sequences can be used for several purposes, such as to reduce the switching frequency and to minimize the NP-voltage ripple [29].
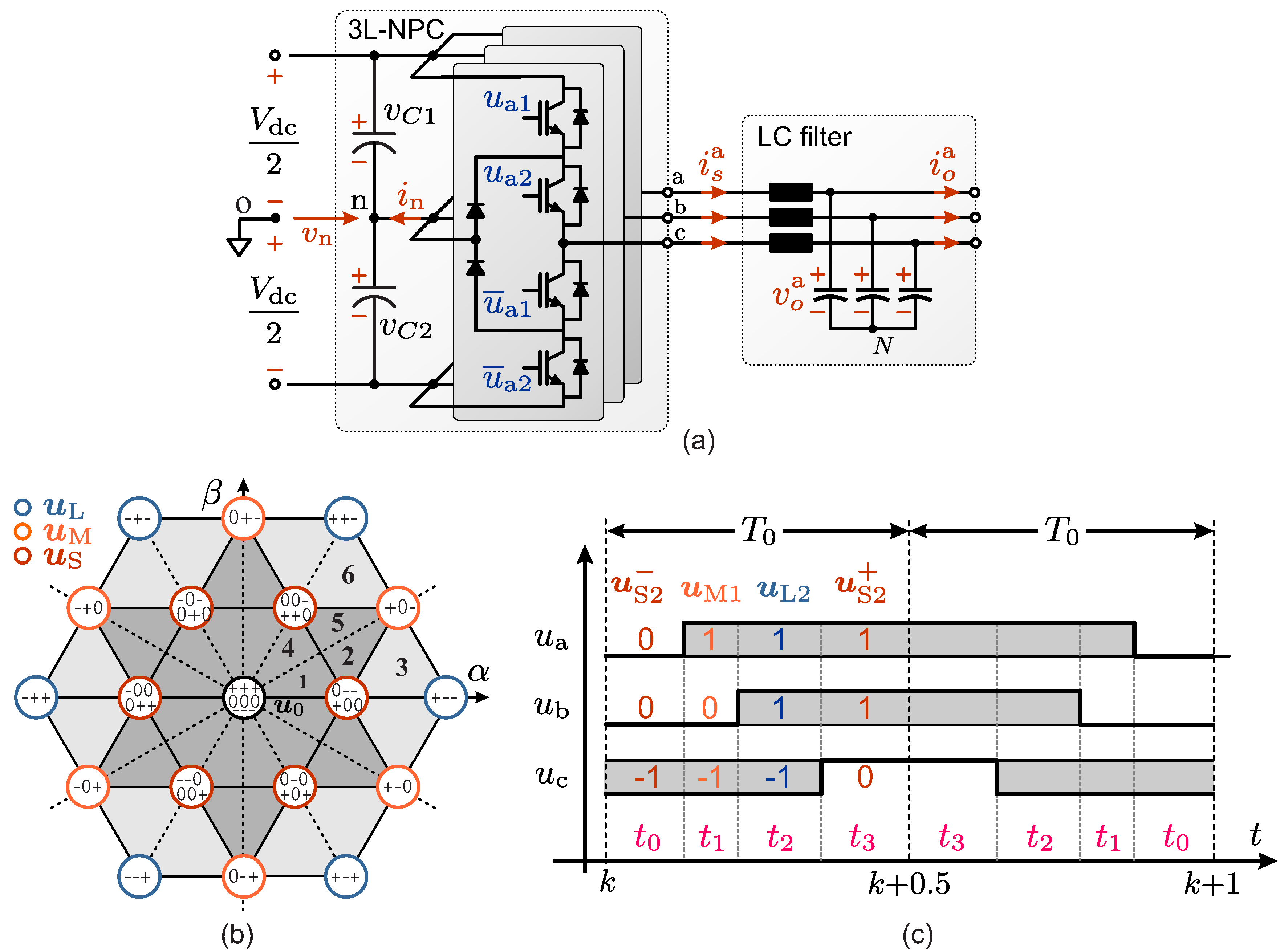
Preprints 93006 g001
Figure 1. 3L-NPC converter: (a) topology; (b) space of switching vectors; (c) 7S-SS for the region R 6 .
Figure 1. 3L-NPC converter: (a) topology; (b) space of switching vectors; (c) 7S-SS for the region R 6 .
Preprints 93006 g001
Based on the above analysis, the seven-segment switching sequence (7S-SS) [29] will be adopted in this work to implement the OSS-MPC strategy for voltage and current control. This switching pattern consists of four SVs, which are arranged in such a way that the transition between two adjacent switching states demands only one switching action. Additionally, each switching period is split into two sub-cycles of duration T 0 = T s / 2 , in which the disposition of the second sub-cycle is a reversal of the arrangement of the first [29], as shown in the example in fig:NPC1](c). Furthermore, the first sub-cycle starts with an N-type small-size SV ( u S − ) and ends with the P-type redundancy ( u S + ). Therefore, each 7S-SS candidate can be defined accordingly as:
S ≜ u S − [ t 0 ] , u 1 [ t 1 ] , u 2 [ t 2 ] , u S + [ 2 t 3 ] , u 2 [ t 2 ] , u 1 [ t 1 ] , u S − [ t 0 ]
where t i is the time in which the ith switching vector is synthesized by the converter, as depicted in Figure 1(c).
Since the twelve internal regions [highlighted in grey in fig:NPC1](b)] have two N-type small-size SVs, each of them is further partitioned in two subregions to reduce the NP-voltage ripple [29]. Thus, to determine which dominant N-type small-size SV should be utilised to assemble the desired switching sequence, the space of SVs is divided in 36 regions as shown in fig:NPC1](b). Then, according to the OSS-MPC principles, a 7S-SS candidate is denoted as S j , where j ∈ R ≜ { 1 , … , 36 } .

3. Cascaded OSS-MPC Strategy for Voltage and Current Control

In this work, a cascaded OSS-MPC scheme will be employed to simultaneously control the voltage and current at an LC filter, while maintaining balanced voltages at the capacitors of the DC-link in a 3L-NPC converter. The overall controller is a predictive control scheme based on the solution to two cascaded optimisation problems.
The proposed control scheme is shown in Figure 2. The first optimisation problem —hereinafter called the outer optimisation loop— computes the optimal switching vectors sequence and duty cycles that minimize a cost function. The cost function is designed to track the desired values of the state vector and minimize the control effort of the converter. The second optimisation problem —hereinafter called the inner optimisation loop— computes an optimal common-mode injection signal (see bottom left-hand side of Figure 2). The common-mode injection signal is designed to balance the neutral-point voltage between the DC-link capacitors.

3.1. Continuous-time model

Let us consider a three-phase 3L-NPC connected to an LC filter, as shown in Figure 1(a). The system of differential equations describing the dynamics of the LC filter can be written as:
L f d i s α β d t + R f i s α β = v s − v o α β
C f d v o α β d t = i s α β − i o α β
Assuming that the DC-link NP-voltage is balanced (i.e., v n = 0 ), the converter output voltage in (2) is equal to v s = V dc 2 u s . Moreover, by rearranging the equations and define the state, input and disturbance vectors as x s = [ i s α i s β v o α v o β ] ⊺ , u s = [ u s α u s β ] ⊺ , and i o = [ i o α i o β ] ⊺ (The superscripts α β in the vectors will be avoided to simplify the notation). The state-space model of the AC side dynamics is then:
x ˙ s = A x s + B u s + E i o
y = C x s
Matrices A , B , and E contain the parameters of the filter and matrix C is the identity matrix.
A = − L − 1 R − L − 1 C f − 1 0 B = V d c 2 L − 1 0 E = 0 − C f − 1
The resistance, inductance, and capacitance matrices are defined as follows:
R = R f I 2 L = L f I 2 C f = C f I 2
The dimensions of the system matrices are A ∈ R 4 × 4 , B ∈ R 4 × 2 , E ∈ R 4 × 2 , x s ( t ) ∈ R 4 × 1 , u s ( t ) ∈ R 2 × 1 , and i o ( t ) ∈ R 2 × 1 .

3.2. Discrete-time model

MPC algorithms use the discrete-time mathematical model of the system, to make predictions of the state vector trajectory, then utilise the predicted values in an optimisation problem and compute the best control action that fulfils the control objectives.
Typically, for the discrete implementation of the continuous-time model, the forward-Euler method is applied. However, as extensively discussed in [31,32], the forward Euler methodology is suitable for implementing nested control loops when two MPC stages are used. For this sort of application an outer MPC algorithm is implemented to regulate the voltages and an inner MPC is utilised to regulate the converter’s output currents [31]. Nevertheless, when nested MPC loops are used, two cost functions are required and a global optimum is not necessarily reached (see [32]).
To reach a global optimum, a single cost function for the load voltage and converter’s output current is required; therefore, with this approach, a single MPC algorithm is required to regulate the voltage and currents in a single optimisation stage (see Figure 2). However, as extensively discussed in [32], when nested voltage-current control loops are implemented in a single stage, the discrete model implemented using the forward Euler method may produce a lack of causality and controllability in the MPC controller; therefore, other continuous to discrete approximations, for instance, the improved Euler method [33] or a two-steps control horizon [32] are recommended. In this work, the discretization of the continuous-time model is performed using the improved Euler method [33]. This is further discussed in this section.

3.2.1. Forward Euler-Based Discrete Time Model

It is assumed in this work that a 7S-SS is applied to the converter during every switching cycle. Considering the forward Euler method, the instantaneous trajectory of the state vector when a switching vector is applied can be computed as:
x s ( l + 1 ) = x s l + T 0 f x s l , u s l , i o l d l
where l ∈ { 0 , 1 , 2 , 3 } is the index for the switching vectors of the sequence. The instantaneous evolution of the state vector prediction at the end of the sub-cycle corresponds to its average trajectory when the seven-segment SS defined by (4) (see [20]) is applied to the system:
x ¯ s [ k + 1 ] = x s [ k ] + T 0 ∑ l = 0 3 d x s d t | t = l d l
To simplify the analysis, every subinterval slope m l = f ( x s l , u s l , i o l ) is approximated using the values of the state and disturbance vector at the sampling instant k as m l ≈ f ( x s [ k ] , u s l , i o [ k ] ) . Therefore, the prediction of the average trajectory can be expressed as:
x ¯ s [ k + 1 ] = A d x s [ k ] + E d i o [ k ] + B d ∑ l = 0 3 u s l d l
where A d = I 4 + T 0 A , E d = T 0 E , and B d = T 0 B . Because for any N-type seven-segment SS, u s 0 = u S − , and u s 3 = u S + , the duty cycles d 0 and d 3 can be combined as d s = d 0 + d 3 which is the duty cycle for the small vectors of the sequence [20]. Then, the following linear representation of the average trajectory can be stated as:
x ¯ s [ k + 1 ] = A d x s [ k ] + E d i o [ k ] + B d U d
where the dwell-time vector d and switching matrix U are defined as:
d = d s d 1 d 2 ∈ D ≜ 0 , 1 3
U = u s u 1 u 2

3.2.2. Improved Euler-Based Discrete Time Model

The improved Euler method is a second-order Runge-Kutta method to compute the solution of ordinary differential equations [33]. In this method, the weighted average of the approximations to the derivative at intermediate points on the solution curve is computed. Specifically, the improved Euler method uses the extreme points of the solution interval (i.e., kth and ( k + 1 )th points). Higher-order Runge-Kutta methods use more intermediate points to increase the accuracy of the solution.
Once again, it is assumed that a 7S-SS is applied by the converter during the complete switching cycle. Considering the improved Euler method, the instantaneous evolution of the state vector is given by the following equation:
x s l + 1 = x s l + T s 2 f x s l , u s l , i o l + f x s l [ k + 1 ] , u s l [ k + 1 ] , i o l [ k + 1 ] d l
The average slope is multiplied by T s because it is the time length between predictions in the interval [ k , k + 1 ] and predictions in the interval [ k + 1 , k + 2 ] . To simplify (14), some assumptions about the states and inputs used for computational purposes are required. Firstly, the slope of the system at the kth time instant is computed with the values measured at the time instant k (i.e., f x s l , u s l , i o l ≈ f x s [ k ] , u s l , i o [ k ] ). Secondly, the slope at the ( k + 1 )th time is computed with the predicted state vector x ¯ s [ k + 1 ] using the forward Euler approximation defined by (12). The switching sequence applied is the same of time instant k (i.e., f x s l [ k + 1 ] , u s l [ k + 1 ] , i o l [ k + 1 ] ≈ f x ¯ s [ k + 1 ] , u s l , i o [ k + 1 ] ). The disturbance vector is assumed to be constant during the switching cycle, but different between switching cycles (i.e., i o [ k ] ≠ i o [ k + 1 ] ). Considering these assumptions, the state vector trajectory is described by:
x s l + 1 = x s l + T s 2 f x s [ k ] , u s l , i o [ k ] + f x s [ k + 1 ] , u s l , i o [ k + 1 ] d l
The slopes m l [ k ] = f x s [ k ] , u s l , i o [ k ] and m l [ k + 1 ] = f x ¯ s [ k + 1 ] , u s l , i o [ k + 1 ] are described by the following equations:
m l [ k ] = A x s [ k ] + B u s l + E i o [ k ]
m l [ k + 1 ] = A x ¯ s [ k + 1 ] + B u s l + E i o [ k + 1 ]
Replacing x ¯ s [ k + 1 ] in (16b), the expression for the slope m l [ k + 1 ] is obtained as follows:
m l [ k + 1 ] = A + 1 2 T s A 2 x s [ k ] + 1 2 T s A B U d + 1 2 T s A E i o [ k ] + B u s l + E i o [ k + 1 ]
Then, the average trajectory of the state vector, using the improved Euler method, is computed as:
x ¯ s [ k + 1 ] = x s [ k ] + T s 2 ∑ l = 0 3 [ m l [ k ] + m l [ k + 1 ] ] d l
Replacing (16a) and (17) into (18), and after some algebraic manipulations, the following expression is obtained:
x ¯ s [ k + 1 ] = I + T s A + 1 4 T s 2 A 2 x s + I + 1 4 T s A T s B U d + 1 2 I + 1 2 T s A T s E i o [ k ] + 1 2 T s E i o [ k + 1 ]
Equation (19) is useful when an observer-predictor computes i o [ k + 1 ] , and the difference between i o [ k ] and i o [ k + 1 ] is sufficiently large. However, if it is assumed that i o [ k ] ≈ i o [ k + 1 ] then the average prediction model is simplified to:
x ¯ s [ k + 1 ] = I + T s A + 1 4 T s 2 A 2 x s + I + 1 4 T s A T s B U d + I + 1 4 T s A T s E i o [ k ]
Discrete-time model in (20) can be written as the linear representation (12) with A d = I + T s A + 1 4 T s 2 A 2 , B d = I + 1 4 T s A T s B , and E d = I + 1 4 T s A T s E . It is straightforward to show that the discrete-time model obtained in (20) is controllable. Thus, the proposed controller can control the converter currents and the capacitor voltages using a single cost function, avoiding a nested control loop structure.

4. C-OSS-MPC formulation

4.1. Reference vector

The objective of the controllers is to keep the voltage of the LC filter capacitors as sinusoidal waveforms. Thus, the reference voltage vector is
v o * [ k + 1 ] = V * e j ω [ k + 1 ] T s
Where V * is the magnitude of the reference voltage vector, and ω is the fundamental frequency of the output voltage ( ω = 2 π f 0 ). The reference current is obtained as a function of the reference voltage. Replacing the reference voltage vector into the dynamic equation of the output voltages yields:
d v o * d t = 1 C f i s * − i o
Solving the equation for i s * we obtain
i s * = ω C f J v o * + i o
where the matrix J is defined as
J = 0 − 1 1 0
It is desirable to constrain the reference current to a maximum value, I m a x . When the amplitude of the reference current is less than the specified limit, the reference current vector is described by equation (23). In the other case, the reference current vector is saturated at I m a x . Therefore, the constrained reference current is represented by the following piece-wise function:
i s * = ω C f J v o * + i o ∥ i s * ∥ 2 < I m a x I m a x ∥ i s * ∥ 2 i s * ∥ i s * ∥ 2 ≥ I m a x
Thus, the reference state vector is
x s * [ k + 1 ] = i s * v o *

4.2. Cost function

At the heart of the MPC strategy lies the cost function. In the cost function, the variables related to the control objectives are weighted to choose the best possible action. In FCS-MPC schemes, the cost function is most commonly designed to minimize the tracking error [34]; however, it has been shown that FCS-MPC strategies without penalization of the control effort are equivalent to quantised dead-beat controllers [15]. Deadbeat controller features fast dynamic response [35] but they have poor robustness against model mismatches, parameter uncertainties, and noise on measured variables [36]. To alleviate the unwanted effects of deadbeat controllers, the control effort is usually penalised in the cost function [35]. In the control proposed in this work, the outer MPC loop has two objectives: minimise the tracking error between the state vector and its reference, and penalize the control effort. Therefore, the following cost function is defined:
J ( U j , d j ) = ∥ x s [ k + 1 ] − x s * [ k + 1 ] ∥ Q 2 + λ u ∥ u [ k + 1 ] − u s s ∥ 2 2
The positive-definite matrix Q = diag( λ i , λ i , λ v , λ v ) is used to trade-off the control objectives of the state vector tracking. Similarly, the weighting factor λ u is used to penalize the control effort. The optimisation variable of the problem is the average switching vector, u ( k ) . The average switching vector is the product between the switching matrix and duty cycle vector as u ( k ) = U d .
Firstly, the term of the cost function used to penalize the reference tracking error will be reformulated as a function of the average switching vector u ( k ) . Replacing (12) in (27), yields:
∥ B d u − x s * [ k + 1 ] − A d x s [ k ] − E d i o [ k ] ︸ κ [ k ] ∥ Q 2
The second term of the cost function in eq. (27) has the vector u s s . Vector u s s is the steady-state control action. The steady-state control action is the input vector needed to drive the system towards the steady-state solution. The expression for this vector is obtained by solving the circuit of Figure 3 for u s s . The steady-state control input u s s is defined as:
u s s = 2 V d c 1 − ω 2 L f C f I 2 + ω R f C f J v o * + R f I 2 + ω L f J i o
Finally, the cost function for the optimisation problem can be written as:
J j ( U j , d j ) = ∥ B d u ( k ) − κ ∥ Q 2 + λ u ∥ u ( k ) − u s s ∥ 2 2

4.3. Optimisation problem

In OSS-MPC, the optimal switching sequence (OSS) is obtained by solving an optimisation problem. The solution must comply with constraints such that the sum of leg duty cycles is equal to one, and each duty cycle must be equal to or greater than zero. Therefore, the optimisation problem to be solved is the following:
{ U ★ , d ★ } = arg min U j { min d j J j ( U j , d j ) }
s . t . 1 ⊺ d = 1
d j ≥ 0
The optimisation problem has the same form as the one solved in [22]. Therefore, the same optimiser will be used. Thus, the usual strategy to solve MPC problems with 3L-NPC converters of evaluating each region R j ∈ { R 1 , … , R 24 } of the space of vectors is avoided.

5. Solution to the outer optimisation problem

In this section, the relaxed optimisation problem will be solved to obtain the optimal switching vector sequence and its corresponding duty cycles to be applied during the next sampling instant. Two cases of the problem are distinguished; First, the linear modulation stage where the duty cycles are positive. Second, the overmodulation stage where the duty cycle of the small switching vectors becomes negative.

5.1. Non-negative duty cycles: the linear modulation stage

5.1.1. Relaxed optimisation problem

To relax the optimisation problem, the inequality constraints are removed from the problem formulation. The relaxed optimisation problem is then stated as
min d J j ( U j , d j )
s . t . 1 ⊺ d = 1
Expanding the cost function yields:
J j = B d u − κ ⊺ Q B d u − κ + λ u u − u s s ⊺ u − u s s
The following expression is obtained,
J j = u ⊺ Q ′ + λ u I 2 u − 2 u ⊺ B d ⊺ Q κ + λ u u s s + λ u u s s ⊺ u s s + κ ⊺ Q κ
where Q ′ is the modified weight matrix, Q ′ = B d ⊺ Q B d . The elements of the switching matrix U j ∈ R 2 × 3 are the vectors of the switching sequence:
U j = u s α u 1 α u 2 α u s β u 1 β u 2 β

5.1.2. Solution of the relaxed optimisation problem

Considering the equality constraint of the relaxed optimisation problem, the duty cycles for the small switching vectors, as a function of the remaining duty cycles, can be written as:
d S j = 1 − d 1 j − d 2 j
An auxiliar variable, d η j , is defined to eliminate the dependent variable d S from the optimisation vector d j :
d η j = d 1 j d 2 j ⊺
The relationship between d j and d η j is the following:
d j = − 1 − 1 1 0 0 1 ︸ M d η j + 1 0 0 ︸ N
Then, u = U d = U M d η j + N = U M d η j + U N and u ⊺ = d ⊺ U ⊺ = M d η j + N ⊺ U ⊺ = d η j ⊺ M ⊺ + N ⊺ U ⊺ . The cost function in terms of d η j is
J = d η j ⊺ M ⊺ U ⊺ Q ′ + λ u I 2 U M d η j + 2 d η j M ⊺ U ⊺ Q ′ + λ u I 2 U N − 2 d η j M ⊺ U ⊺ B d ⊺ Q κ + λ u u s s + N ⊺ U ⊺ Q ′ + λ u I 2 U N − 2 N ⊺ U ⊺ B d ⊺ Q κ + λ u u s s + κ ⊺ Q κ + λ u u s s ⊺ u s s
Computing the gradient of J with respect to d η j and making it equal to zero, yields:
∇ J d η j = 2 M ⊺ U ⊺ Q ′ + λ u I 2 U M d η j + 2 M ⊺ U ⊺ Q ′ + λ u I 2 U N − 2 M ⊺ U ⊺ B d ⊺ Q κ + λ u u s s = 0
Reorganizing (40) to leave the terms related to the duty cycles on the left, (41) is obtained:
M ⊺ U ⊺ Q ′ + λ u I 2 U M d η j = M ⊺ U ⊺ B d ⊺ Q κ + λ u u s s − M ⊺ U ⊺ Q ′ + λ u I 2 U N
Solving the equation for d η j yields:
d η j = U M − 1 u u n c − U M − 1 U N
The unconstrained control action ( u u c ) is defined as:
u u c = Q ′ + λ u I 2 − 1 B d ⊺ Q κ + λ u u s s
Now, it is required to map the solution back to its original variables. Replacing (42) in (38), yields:
d r j = M U M − 1 N − M U M − 1 U N u u c 1
The optimal duty cycles for the linear modulation stage are computed using the ( 3 × 3 ) matrix:
d r j = 1 Δ u 1 β − u 2 β u 2 α − u 1 α u 1 × u 2 u 2 β − u s β u s α − u 2 α u 2 × u s u s β − u 1 β u 1 α − u s α u s × u 1 u u c , α u u c , β 1
where Δ is the determinant of matrix product U M − 1 :
Δ = u S × u 1 + u 2 × u S + u 1 × u 2
Where u x × u y = u x α u y β − u x β u y α denotes the cross product.

6. Optimal Solution

In the previous section, the relaxed solution to the optimisation problem was calculated. The relaxed duty cycles vector d r j is the local solution for each region R j ∈ R of the control hexagon V . The relaxed solution computed with (Section 5.1.1) fulfills the equality constraint 1 ⊺ d = 1 . Thus, all regions can be mapped onto u u c in the α β -plane. However, only one region fulfils the non-negativity constraint [20]. The non-negativity constraint can then be considered in the solution with a simple methodology (as reported in [20,22]). The methodology introduced therein also reduces the computational burden avoiding the search over all 24 regions of the control region V to only four. The methodology will be explained in this section.
Firstly, considering the α β -plane shown in Figure 4(a) with the Space of Vectors of the 3L-NPC is divided into 12 regions. The algorithm seeks the region where u u c is located, and then the three sectors in that region are evaluated in the control algorithm. Given that u u c is the desired solution of the optimisation problem, its angle is used to find the optimal region in the plane. The optimal sector S ★ is obtained from the following equation:
S ★ = floor { 6 π tan − 1 u u c , β u u c , α } + 1
When the optimal sector is calculated, the duty cycles of the switching sequences contained in it are evaluated. The sector whose duty cycles comply with the non-negativity constraint is the optimal sector, and thus, the optimal switching sequence is found.
Preprints 93006 g004
Figure 4. Control region of the 3L-NPC. (a) Hexagon divided into 12 sectors to reduce the computational burden of the OSS-MPC algorithm, and (b) close-up look into sectors S 1 - S 2 .
Figure 4. Control region of the 3L-NPC. (a) Hexagon divided into 12 sectors to reduce the computational burden of the OSS-MPC algorithm, and (b) close-up look into sectors S 1 - S 2 .
Preprints 93006 g004
The conventional enumeration algorithm can be reduced to only 3 regions after the sector has been identified. Each sector has three candidate switching sequences, but only one of them fulfills the non-negativity constraint. Thus, the optimal pair { U ★ , d ★ } is found evaluating the non-negativity condition over the duty cycles vector of each candidate region. However, if u u c falls outside the control region V (e.g., see u u c ( 2 ) in Figure 4(b)) then none of the candidate switching sequences fulfil the non-negativity constraint.
The aforementioned case occurs during a transient operation. The candidate switching sequence is then reduced to one and is built by the medium and large switching vectors belonging to the only outer region that intersects the optimal sector. The case is further analyzed in the next subsection.

6.1. Handling the negative duty cycles: the overmodulation stage

6.1.1. Relaxed optimisation problem

The unconstrained average switching vector goes outside the hexagon, thus the duty cycle for the small switching vector becomes negative. Defining d S j = 0 , the optimisation variable becomes
d j = 0 d 1 j d 2 j
Consider the equality constraint
1 ⊺ 0 d 1 j d 2 j = 1
Notice that one of the two optimisation variables is dependent. Thus, if we set d 2 j to be dependent of d 1 j , we can find an auxiliary vector to reduce the equality-constrained optimisation problem into an unconstrained optimisation problem
d j = 0 1 − 1 ︸ M ′ d 1 j + 0 0 1 ︸ N ′
Then, u = U d = M ′ d j + N ′ = u 1 − u 2 d 1 + u 2 and u ⊺ = d j ⊺ U ⊺ = M ′ d j + N ′ ⊺ U ⊺ = u 1 − u 2 ⊺ d 1 + u 2 ⊺ . The cost function is
J = u 1 − u 2 ⊺ Q ′ + λ u I 2 u 1 − u 2 d 1 2 + 2 u 1 − u 2 ⊺ Q ′ + λ u I 2 u 2 d 1 − 2 u 1 − u 2 ⊺ B d ⊺ Q u d b ′ + λ u u s s d 1 + u 2 ⊺ Q ′ + λ u I 2 u 2 − 2 u 2 ⊺ B d ⊺ Q κ + λ u u s s + κ ⊺ Q κ + λ u u s s ⊺ u s s

6.1.2. Solution of the relaxed optimisation problem

The unconstrained optimisation problem is solved by setting to zero the derivative of the cost function with respect to the optimisation variable
d d ( d 1 j ) J = 2 u 1 − u 2 ⊺ Q ′ + λ u I 2 u 1 − u 2 d 1 + 2 u 1 − u 2 ⊺ Q ′ + λ u I 2 u 2 − 2 u 1 − u 2 ⊺ B d ⊺ Q κ + λ u u s s = 0
Solving it for d 1 yields:
d 1 = u 1 − u 2 ⊺ B d ⊺ Q κ + λ u u s s u 1 − u 2 ⊺ Q ′ + λ u I 2 u 1 − u 2 − u 1 − u 2 ⊺ Q ′ + λ u I 2 u 2 u 1 − u 2 ⊺ Q ′ + λ u I 2 u 1 − u 2
The matrix Q ′ + λ u I 2 corresponds to a scalar multiplied by the identity matrix. Bearing on mind that u u c = Q ′ + λ u I 2 − 1 B d ⊺ Q κ + λ u u s s , the optimal duty cycle d 1 ★ is
d 1 j ★ = ( u 1 − u 2 ) ⊺ ( u u c − u 2 ) ( u 1 − u 2 ) ⊺ ( u 1 − u 2 )
Notice that the denominator of d 1 j ★ is the length between a large and medium vector in the hexagon frontier (see Figure 4(b)), thus:
∥ Δ u ∥ 2 2 = ( u 1 − u 2 ) ⊺ ( u 1 − u 2 ) = 4 9
Then, the optimal solution for the overmodulation stage is:
d 1 j ★ = mid { 0 , 9 4 ( u 1 − u 2 ) ⊺ ( u u n c − u 2 ) , 1 }
d 2 j ★ = 1 − d 1 j

7. Inner optimisation problem

The objective of the inner optimisation loop is to compute an optimal common-mode signal u 0 ★ to balance the DC-link capacitors of the 3L-NPC converter. The strategy assumes that a PWM stage is used to synthesize the solution obtained from the outer optimisation loop. To this end, the optimal SS is mapped into a three-phase reference signal D a b c = [ D a D b D c ] ⊺ ∈ [ − 1 , 1 ] 3 obtained as [22]:
D a b c = d 1 ★ u a b c , 1 ★ + d 2 ★ u a b c , 2 ★ + 1 2 d S ★ u a b c , 0 ★ + u a b c , 3 ★
in which u a b c , l ★ = T α β − 1 u s l ★ are the three-phase switching states that produce the optimal SS. The optimal common-mode signal is the solution to the following optimisation problem:
u o ★ = min u o v n [ k + 1 ] − v n * 2
s . t . u o [ k ] ∈ [ − Δ o , Δ o ]
in which v n * is the reference value of the DC-link NP-voltage, v n [ k + 1 ] is the discrete-time model of the NP voltage and Δ o is a time-varying saturation level which represents the voltage available in the DC-link. The solution to the optimisation problem yields the following equation:
u o ★ = mid { − Δ o , − α [ k ] − v n * − v n [ k ] β [ k ] , Δ o }
where α [ k ] and β [ k ] are determined at each sampling instant according to:
α [ k ] = T s C 1 + C 2 ∑ x ∈ P | D x | i x β [ k ] = T s C 1 + C 2 ∑ x ∈ P sgn { D x } i x
where x ∈ P = { a , b , c } . The time-varying saturation level is defined as:
Δ o [ k ] = min { 1 − | D x [ k ] | }
Finally, the three-phase reference signals sent to the PWM modulator are:
D a b c ★ = D a b c + u 0 ★
For a more throughout explanation of the inner optimisation loop, the reader is referred to [22].

8. Hardware-in-the-Loop (HIL) Results

In this section, Hardware-in-the-Loop (HIL) results are shown to validate the proposed controller. The 3L-NPC converter, LC filter and loads are emulated using PLECS-RT box 1 HIL platforms with a time-step of 5 μ s. The control system is separately implemented using a dSPACE MicroLabBox platform. This dSpace controller is equipped with a Freescale QorIQ P5020 dual-core 2 GHz processor, for number crunching, and a Kintex-7 XC7K325-T FPGA. The FPGA handles the AD conversion, performs an In-Phase Disposition PWM strategy and implements a dead time of 1 μ s for each switching device; the HIL system is shown in Figure 5(a). The processor computes the Clark transform of the measured three-phase variables, executes the optimisation algorithm, and computes the appropriate three-phase reference signals for the modulator. The loads considered for the study are a three-phase resistive load bank and a nonlinear load implemented using a three-phase diode rectifier with a capacitor and resistor connected in parallel at the DC side, as shown in Figure 5(b). The parameters of the system are shown in Table 1 and are similar to those used in a previous work (see [23]).
The performance of the controllers is evaluated using the following goodness factors: RMS error (RMSE), percentage of voltage error (Ev) and total harmonic distortion (THD). The percentage of error is defined as follows:
E v [ % ] = 100 ∥ v * ∥ 1 N p ∑ k ∈ P ∥ v ( k ) − v * ( k ) ∥ 2 2
where P = { 1 , 2 , … , N p } is the set of indices of the measurements vector, and N p = T 1 / T s is the total number of elements in the vector. T 1 is the period of the fundamental frequency, and T s is the period of the sampling frequency. Whenever the desired reference amplitude is unknown, the root-mean-square error (RMSE) will be used. The RMS error is defined as follows:
RMSE ( x − x * ) = 1 N p ∑ k ∈ P ∥ x ( k ) − x * ( k ) ∥ 2 2
A one-step delay compensation is carried out to compensate for the computational delay introduced by the digital platform. The state vector x s [ k + 1 ] is computed using (20) with the values measured at the k t h instant, and the switching sequence applied during the previous switching interval. The voltage reference v o [ k + 1 ] is computed shifting the phase of the reference signal one step ahead. The load output current i o [ k + 1 ] is estimated using the Lagrange extrapolation technique. The Lagrange extrapolation technique uses the actual and past measurements of the signal to estimate its future value. The load output current i o [ k + 1 ] is computed as follows [37]:
i o [ k + 1 ] = 4 i o [ k ] − 6 i o [ k − 1 ] + 4 i o [ k − 2 ] − i o [ k − 3 ]
The estimated load output current has an RMS error of 0.0603 [A] in the α -component, and 0.0640 [A] in the β -component for the worst-case scenario (nonlinear load). The estimated and measured load output current are shown in Figure 6. As shown in this figure, the estimated current tracks relatively well the measured current.
In Figure 7(a), the output voltages when the system operates without load are shown. The reference voltage has an amplitude of 300 [V] with a frequency of 50[Hz]. For this condition, the load output voltages have a voltage error of 2.04% and a THD of 1.74%. Then, a three-phase resistive load is connected as in Figure 7(d). In this condition, the voltage error is 2.05% and the THD is 1.03%. When a nonlinear load is connected, as in Figure 7(g), the voltage error is 2.83%. The harmonic spectrum for the load output voltage and load output current are shown in Figure 8(a)-(b). The voltage THD in this case is 2.73% with the presence of 5th and 7th harmonics, which are produced by the bridge rectifier. In Figure 7(b)-(h) the load output current is shown for the three aforementioned cases. Finally, in Figure 7(c)-(i), the DC-link capacitor voltages are shown. The control strategy is capable of maintaining the DC-link voltages balanced and well regulated, for all operating conditions with very small oscillations.
The transient operation of the controlled system is studied in Figure 9 considering changes in the reference voltage amplitude. The variables are presented in the synchronous reference frame to verify the settling time of the load output voltage.
The settling time is computed as the time required by the output voltage to reach and stay within 5% of the desired voltage. In Figure 9(a) the reference voltage receives a step variation from 300 [V] to 100 [V] at t = 0.2 [s]. The voltage error amounts to 5.98% under steady-state conditions. The rise in voltage error results from the reduction in the amplitude of the reference voltage. In Figure 9(b), the reference voltage varies from 100 [V] to 300 [V] at t = 0.2 [s]. In this case, the load output voltage manages to stay within the band of 5% around the desired voltage. Thus, the settling time is 1.03 [ms] approximately.
Notice that a relatively low steady-state error is presented in the HIL results shown in Figure 9 a and b. This small steady-state error is produced because there is not an integrator in the MPC algorithm [38,39]. If steady state error is a must, then the state space matrix A [see (7)] must be augmented with additional states to represent the integrator [38]; however, this topic is considered outside the scope of this work.
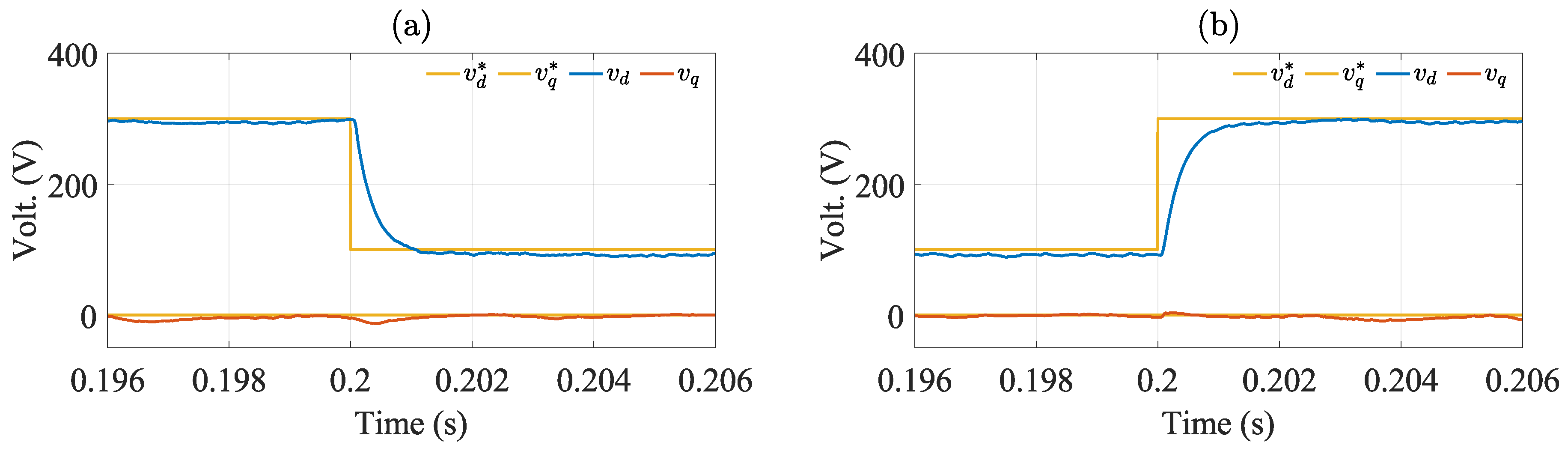
Preprints 93006 g009
Figure 9. Transient operation of the system for reference voltage step. (a) voltage step from 300 [V] to 100 [V], (b) voltage step from 100 [V] to 300 [V].
Figure 9. Transient operation of the system for reference voltage step. (a) voltage step from 300 [V] to 100 [V], (b) voltage step from 100 [V] to 300 [V].
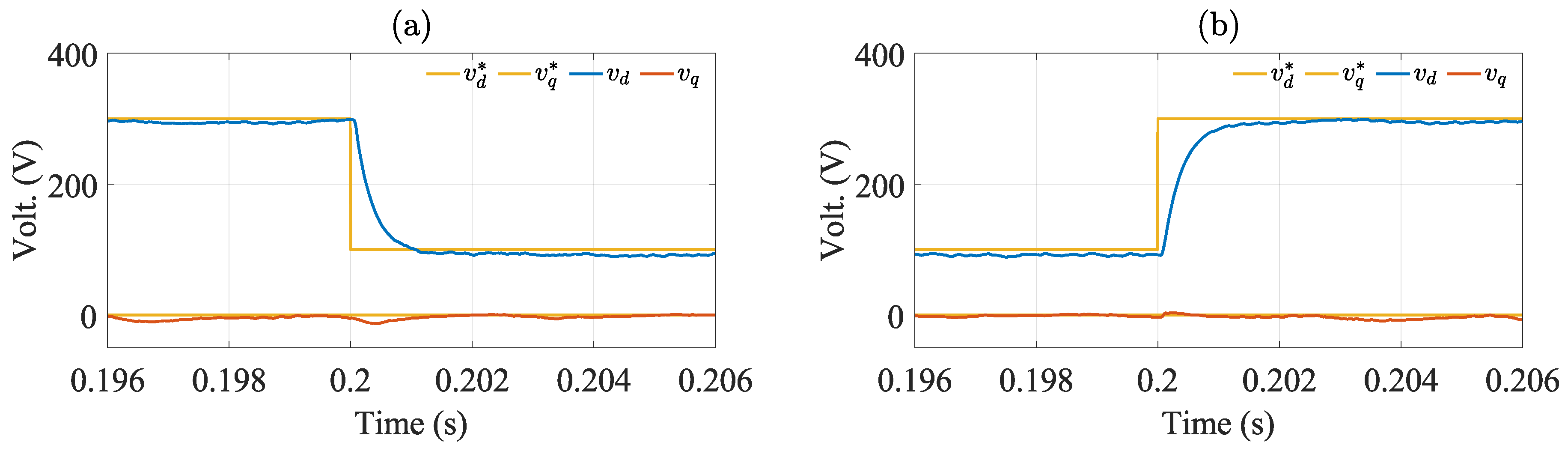
Preprints 93006 g009
Figure 10 shows the operation of the system for a load step. A dip occurs in the load output voltage, as shown in Figure 10(a), and takes 1 [ms] approximately to recover. Notice that there is a sudden increase in the inductor reference current to 10 A approximately, and the current features a fast dynamic response to the step change.
The cost function of (30) has two terms: the first term penalizes the deviation of the system states from a reference vector and the second term penalizes the control effort of the converter. The control effort is penalized in the cost function by the deviation between the optimisation variable u ( k ) and the steady-state control action u s s . The weight of this deviation on the optimisation problem is set by the parameter λ u . Increasing λ u will lead the converter’s response to move closer to open-loop operation since u s s depends only on the load reference voltage and load output current. The system’s performance with a logarithmic variation of the parameter λ u is shown in Figure 11. The results are obtained considering a three-phase resistive load at the LC filter terminals. The best trade-off in terms of voltage error between open-loop and closed-loop operation of the converter is achieved when λ u = 10 , as shown in Figure 11(a). When λ u is increased, the response of the system tends toward u s s which does not penalize the voltage error. Thus, the voltage error increases.
As shown in Figure 11(b), the voltage THD presents slight variations around 1%, as shown in Figure 11(b). The system’s transient response is also dependent on the value of λ u . A trade-off between settling time and overshoot must be reached, as shown in Figure 12. Increasing λ u up to 100 will reduce the settling time of the system but increase the voltage overshoot. However, for λ u > > 100 , the system response will present a damped sinusoidal oscillation which increases the settling time.
Preprints 93006 g011
Figure 11. System performance over variation of λ u .
Figure 11. System performance over variation of λ u .
Preprints 93006 g011
Preprints 93006 g012
Figure 12. Transient operation of the system for different values of λ u .
Figure 12. Transient operation of the system for different values of λ u .
Preprints 93006 g012

9. Conclusions

In this paper, an Optimal Switching Sequence MPC algorithm was proposed for the three-level neutral-point-clamped inverter with an output LC filter. The strategy is an extension of the Cascaded Optimal Switching Sequence MPC proposed in the literature for current and direct power control of active front-end 3L-NPC inverters. The control objectives of the algorithm were two: (1) achieve good tracking performance for the LC filter variables, and (2) maintain balanced the neutral-point voltage between the DC-link capacitors of the converter. To achieve the objectives, the strategy solves two cascaded optimisation problems. The first optimisation problem -called the outer optimisation loop- computes the optimal sequence of switching vectors and their corresponding duty cycles to achieve the objectives related to tracking the AC side variables. Then, the optimal solution of the outer optimisation loop is used by an inner optimisation loop to compute an optimal common-mode signal designed to balance the neutral-point voltage between the DC-link capacitors. A discrete-time model based on the improved Euler discretization method was used to predict the future values of the state vector trajectory. Notice that this methodology allows the implementation of a single-stage MPC algorithm to regulate the load voltage and the converter output current.
Experimental results are provided to validate the performance of the proposed strategy using PLEXIM Hardware-in-the-Loop (HIL) platform RT Box 1 to emulate the power electronics stage, and the control algorithm was executed by the dSPACE MicroLabBox control platform. Three cases were considered in steady-state operation: (1) system performance without load, (2) system performance with linear load, and (3) system performance with nonlinear load. In all cases, the MPC algorithm is capable of achieving good tracking of the load voltage reference with a small error and low THD. Also, the strategy is capable of maintaining well-balanced voltages at the DC-link capacitors.

Author Contributions

Conceptualization, Felipe Herrera, Andrés Mora, Roberto Cárdenas and Jose Rodriguez; Formal analysis, Felipe Herrera, Andrés Mora, Roberto Cárdenas, Matías Díaz and Marco Rivera; Funding acquisition, Roberto Cárdenas, Matías Díaz and Jose Rodriguez; Investigation, Felipe Herrera, Jose Rodriguez and Marco Rivera; Methodology, Andrés Mora and Roberto Cárdenas; Project administration, Roberto Cárdenas; Resources, Matías Díaz; Software, Felipe Herrera, Matías Díaz and Marco Rivera; Supervision, Andrés Mora and Roberto Cárdenas; Validation, Felipe Herrera, Andrés Mora and Roberto Cárdenas; Writing – original draft, Felipe Herrera and Andrés Mora; Writing – review & editing, Andrés Mora, Roberto Cárdenas, Matías Díaz, Jose Rodriguez and Marco Rivera. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Fondecyt grants numbers 1221392 and 1231030. The support of Fondequip EQM210117 and Basal grant FB0008 is kindly acknowledged.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
7S-SS Seven Segments Switching Sequence
DC Direct Current
AC Alternate Current
FPGA Field Programmable Gate Array
FCS-MPC Finite Control Set Model Predictive Control
M 2 P C Modulated Model Predictive Control
HIL Hardware in the Loop
LC-filter Inductance Capacitor Filter
MIMO Multiple-Input Multiple-Output
MPC Model Predictive Control
NPC Neutral Point Clamped
OSS Optimal Switching Sequence
OSV Optimal Switching Vector
PWM Pulse Width Modulation
RT Real Time
SISO Single-Input Single-Output
THD Total Harmonic Distortion
UPS Uninterruptible Power Supply
VFD Variable Frequency Drives

References

  1. Cárdenas, R.; Espina, E.; Clare, J.; Wheeler, P. Self-Tuning Resonant Control of a Seven-Leg Back-to-Back Converter for Interfacing Variable-Speed Generators to Four-Wire Loads. IEEE Transactions on Industrial Electronics 2015, 62, 4618–4629. [Google Scholar] [CrossRef]
  2. Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cárdenas-Dobson, R.; Martínez-Gómez, M.; Sáez, D. Distributed Control Strategies for Microgrids: An Overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
  3. Loh, P.C.; Newman, M.; Zmood, D.; Holmes, D. A comparative analysis of multiloop voltage regulation strategies for single and three-phase UPS systems. IEEE Transactions on Power Electronics 2003, 18, 1176–1185. [Google Scholar] [CrossRef]
  4. Cortes, P.; Ortiz, G.; Yuz, J.I.; Rodriguez, J.; Vazquez, S.; Franquelo, L.G. Model Predictive Control of an Inverter With Output LC Filter for UPS Applications. IEEE Transactions on Industrial Electronics 2009, 56, 1875–1883. [Google Scholar] [CrossRef]
  5. Alhosaini, W.; Zhao, Y. A Model Predictive Voltage Control using Virtual Space Vectors for Grid-Forming Energy Storage Converters. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC); 2019; pp. 1466–1471. [Google Scholar] [CrossRef]
  6. Xue, C.; Zhou, D.; Li, Y. Finite-Control-Set Model Predictive Control for Three-Level NPC Inverter-Fed PMSM Drives With LC Filter. IEEE Transactions on Industrial Electronics 2021, 68, 11980–11991. [Google Scholar] [CrossRef]
  7. Dragičević, T. Model Predictive Control of Power Converters for Robust and Fast Operation of AC Microgrids. IEEE Transactions on Power Electronics 2018, 33, 6304–6317. [Google Scholar] [CrossRef]
  8. Diaz, M.; Cardenas, R.; Espinoza, M.; Rojas, F.; Mora, A.; Clare, J.C.; Wheeler, P. Control of Wind Energy Conversion Systems Based on the Modular Multilevel Matrix Converter. IEEE Transactions on Industrial Electronics 2017, 64, 8799–8810. [Google Scholar] [CrossRef]
  9. Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Industrial Electronics Magazine 2014, 8, 16–31. [Google Scholar] [CrossRef]
  10. Rodriguez, J.; Cortes, P. Model Predictive Control. Predictive Control of Power Converters and Electrical Drives, 2012; 31–39. [Google Scholar] [CrossRef]
  11. Kouro, S.; Perez, M.A.; Rodriguez, J.; Llor, A.M.; Young, H.A. Model Predictive Control: MPC’s Role in the Evolution of Power Electronics. IEEE Industrial Electronics Magazine 2015, 9, 8–21. [Google Scholar] [CrossRef]
  12. Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control-A Simple and Powerful Method to Control Power Converters. IEEE Transactions on Industrial Electronics 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
  13. Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model Predictive Control of Power Electronic Systems: Methods, Results, and Challenges. IEEE Open Journal of Industry Applications 2020, 1, 95–114. [Google Scholar] [CrossRef]
  14. Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortes, P.; Ammann, U. Predictive Current Control of a Voltage Source Inverter. IEEE Transactions on Industrial Electronics 2007, 54, 495–503. [Google Scholar] [CrossRef]
  15. Karamanakos, P.; Geyer, T. Guidelines for the Design of Finite Control Set Model Predictive Controllers. IEEE Transactions on Power Electronics 2020, 35, 7434–7450. [Google Scholar] [CrossRef]
  16. Tarisciotti, L.; Zanchetta, P.; Watson, A.; Clare, J.; Degano, M.; Bifaretti, S. Modulated model predictive control (M2PC) for a 3-phase active front-end. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition; 2013; pp. 1062–1069. [Google Scholar] [CrossRef]
  17. Vazquez, S.; Marquez, A.; Aguilera, R.; Quevedo, D.; Leon, J.I.; Franquelo, L.G. Predictive Optimal Switching Sequence Direct Power Control for Grid-Connected Power Converters. IEEE Transactions on Industrial Electronics 2015, 62, 2010–2020. [Google Scholar] [CrossRef]
  18. Karamanakos, P.; Nahalparvari, M.; Geyer, T. Fixed Switching Frequency Direct Model Predictive Control With Continuous and Discontinuous Modulation for Grid-Tied Converters With LCL Filters. IEEE Transactions on Control Systems Technology, 2020; 1–16. [Google Scholar]
  19. Xu, B.; Liu, K.; Ran, X. Computationally Efficient Optimal Switching Sequence Model Predictive Control for Three-Phase Vienna Rectifier Under Balanced and Unbalanced DC Links. IEEE Transactions on Power Electronics 2021, 36, 12268–12280. [Google Scholar] [CrossRef]
  20. Mora, A.; Cárdenas-Dobson, R.; Aguilera, R.P.; Angulo, A.; Donoso, F.; Rodriguez, J. Computationally Efficient Cascaded Optimal Switching Sequence MPC for Grid-Connected Three-Level NPC Converters. IEEE Transactions on Power Electronics 2019, 34, 12464–12475. [Google Scholar] [CrossRef]
  21. Vazquez, S.; Acuna, P.; Aguilera, R.P.; Pou, J.; Leon, J.I.; Franquelo, L.G. DC-Link Voltage-Balancing Strategy Based on Optimal Switching Sequence Model Predictive Control for Single-Phase H-NPC Converters. IEEE Transactions on Industrial Electronics 2020, 67, 7410–7420. [Google Scholar] [CrossRef]
  22. Mora, A.; Cardenas, R.; Aguilera, R.P.; Angulo, A.; Lezana, P.; Lu, D.D.C. Predictive Optimal Switching Sequence Direct Power Control for Grid-Tied 3L-NPC Converters. IEEE Transactions on Industrial Electronics 2021, 68, 8561–8571. [Google Scholar] [CrossRef]
  23. Zheng, C.; Dragičević, T.; Zhang, Z.; Rodriguez, J.; Blaabjerg, F. Model Predictive Control of LC-Filtered Voltage Source Inverters With Optimal Switching Sequence. IEEE Transactions on Power Electronics 2021, 36, 3422–3436. [Google Scholar] [CrossRef]
  24. Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Transactions on Industry Applications 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
  25. Rodriguez, J.; Bernet, S.; Wu, B.; Pontt, J.O.; Kouro, S. Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives. IEEE Transactions on Industrial Electronics 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
  26. Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A Survey on Neutral-Point-Clamped Inverters. IEEE Transactions on Industrial Electronics 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
  27. Rocha, A.V.; de Paula, H.; dos Santos, M.E.; Filho, B.J.C. Increasing long belt-conveyors availability by using fault-resilient medium voltage AC drives: Part II - Reliability and maintenance assessment. In Proceedings of the 2012 IEEE Industry Applications Society Annual Meeting; 2012; pp. 1–8. [Google Scholar]
  28. Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous power theory and applications to power conditioning; Wiley, 2007; p. 379.
  29. Wu, B. High-Power Converters and AC Drives; Wiley-IEEE Press, 2006.
  30. Leon, J.I.; Kouro, S.; Franquelo, L.G.; Rodriguez, J.; Wu, B. The Essential Role and the Continuous Evolution of Modulation Techniques for Voltage-Source Inverters in the Past, Present, and Future Power Electronics. IEEE Transactions on Industrial Electronics 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
  31. Arias-Esquivel, Y.; Cárdenas, R.; Urrutia, M.; Diaz, M.; Tarisciotti, L.; Clare, J.C. Continuous Control Set Model Predictive Control of a Modular Multilevel Converter for Drive Applications. IEEE Transactions on Industrial Electronics 2023, 70, 8723–8733. [Google Scholar] [CrossRef]
  32. Arias-Esquivel, Y.; Cárdenas, R.; Tarisciotti, L.; Díaz, M.; Mora, A. A Two-Step Continuous-Control-Set MPC for Modular Multilevel Converters Operating With Variable Output Voltage and Frequency. IEEE Transactions on Power Electronics 2023, 38, 12091–12103. [Google Scholar] [CrossRef]
  33. Süli, E.; Mayers, D. An Introduction to Numerical Analysis;; Cambridge University Press, 2003.
  34. Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Transactions on Industrial Electronics 2017, 64, 935–947. [Google Scholar] [CrossRef]
  35. Quevedo, D.E.; Aguilera, R.P.; Geyer, T. Predictive Control in Power Electronics and Drives: Basic Concepts, Theory, and Methods. In Advanced and Intelligent Control in Power Electronics and Drives; Orłowska-Kowalska, T., Blaabjerg, F., Rodríguez, J., Eds.; Studies in Computational Intelligence, Springer International Publishing: Cham, 2014; pp. 181–226. [Google Scholar] [CrossRef]
  36. Mattavelli, P. An improved deadbeat control for UPS using disturbance observers. IEEE Transactions on Industrial Electronics 2005, 52, 206–212. [Google Scholar] [CrossRef]
  37. Yaramasu, V.; Wu, B. Fundamentals of Model Predictive Control. In Model Predictive Control of Wind Energy Conversion Systems; 2017; pp. 117–148. [Google Scholar] [CrossRef]
  38. Hackl, C. MPC with analytical solution and integral error feedback for LTI MIMO systems and its application to current control of grid-connected power converters with LCL-filter. In Proceedings of the 2015 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE); 2015; pp. 61–66. [Google Scholar] [CrossRef]
  39. Norambuena, M.; Lezana, P.; Rodriguez, J. A Method to Eliminate Steady-State Error of Model Predictive Control in Power Electronics. IEEE Journal of Emerging and Selected Topics in Power Electronics 2019, 7, 2525–2530. [Google Scholar] [CrossRef]
Preprints 93006 g002
Figure 2. Proposed control system, composed of an MPC where the load- voltage and the converter’s output current are controlled in a single-stage MPC. Notice that the common mode voltage is obtained using a second MPC algorithm.
Figure 2. Proposed control system, composed of an MPC where the load- voltage and the converter’s output current are controlled in a single-stage MPC. Notice that the common mode voltage is obtained using a second MPC algorithm.
Preprints 93006 g002
Preprints 93006 g003
Figure 3. Circuit diagram to obtain the steady-state control action.
Figure 3. Circuit diagram to obtain the steady-state control action.
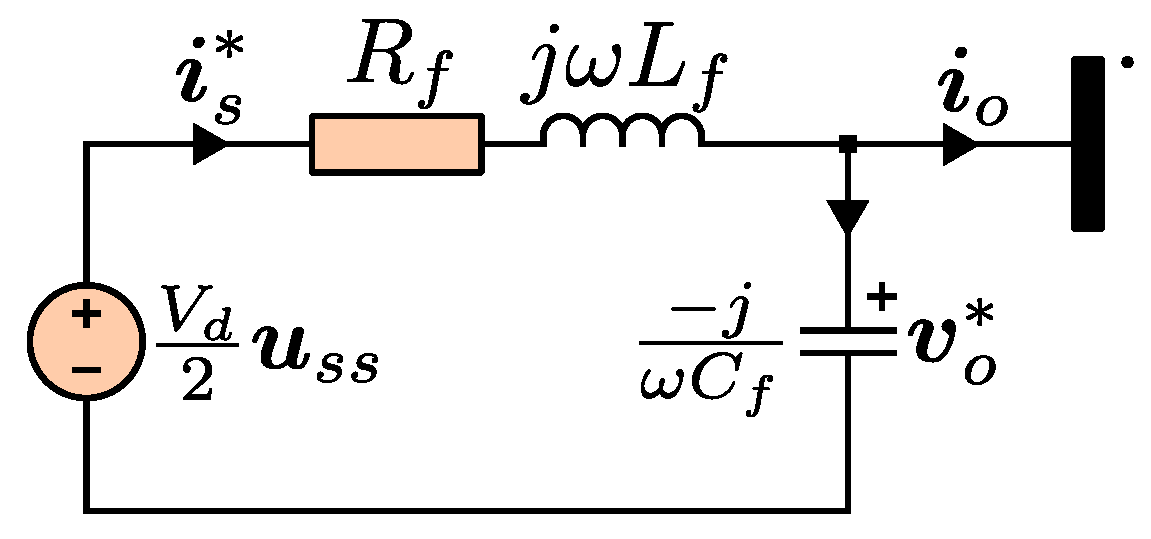
Preprints 93006 g003
Preprints 93006 g005
Figure 5. (a) HIL platform used to perform the experiments, and (b) topology of the nonlinear load.
Figure 5. (a) HIL platform used to perform the experiments, and (b) topology of the nonlinear load.
Preprints 93006 g005
Preprints 93006 g006
Figure 6. Estimated and measured current when a nonlinear load is connected. (a) α -component of the load current, and (b) β -component of the load current.
Figure 6. Estimated and measured current when a nonlinear load is connected. (a) α -component of the load current, and (b) β -component of the load current.
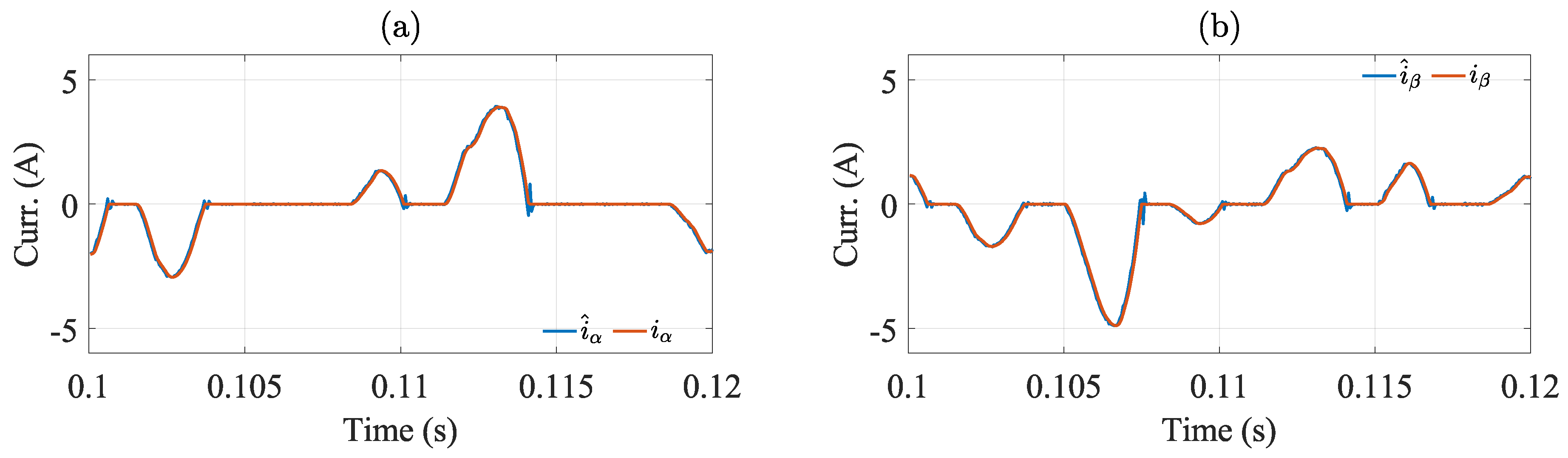
Preprints 93006 g006
Preprints 93006 g007
Figure 7. Steady-state results for different load conditions. (a,d,g) Load output voltage without load, with resistive load and with nonlinear load, (b,e,h) load output current without load, with resistive load and with nonlinear load, and (c,f,i) DC-link capacitor voltages without load, with a resistive linear load and nonlinear load.
Figure 7. Steady-state results for different load conditions. (a,d,g) Load output voltage without load, with resistive load and with nonlinear load, (b,e,h) load output current without load, with resistive load and with nonlinear load, and (c,f,i) DC-link capacitor voltages without load, with a resistive linear load and nonlinear load.
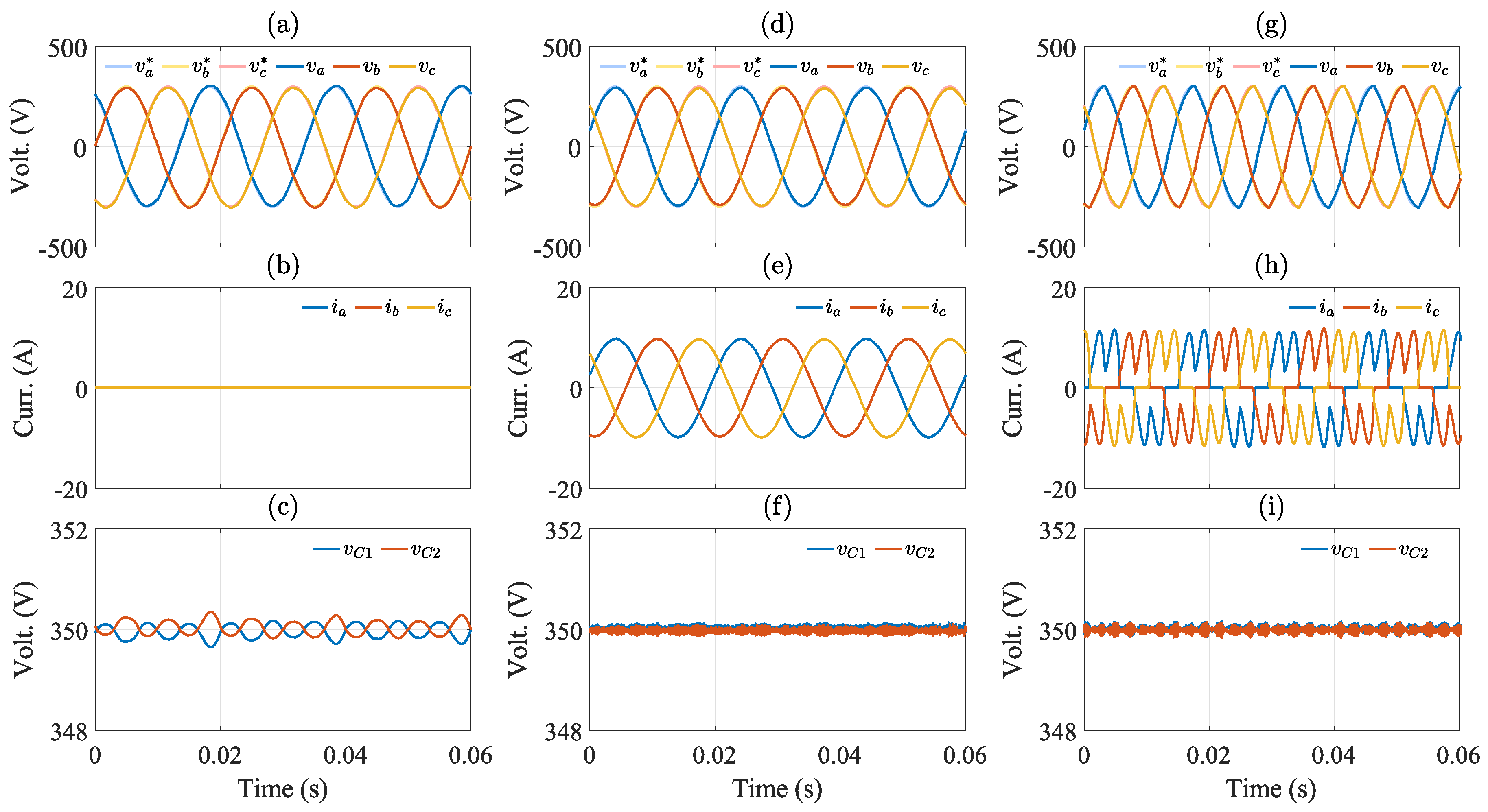
Preprints 93006 g007
Preprints 93006 g008
Figure 8. Harmonic spectrum of (a) load output voltage, and (b) load output current when a nonlinear load is connected.
Figure 8. Harmonic spectrum of (a) load output voltage, and (b) load output current when a nonlinear load is connected.
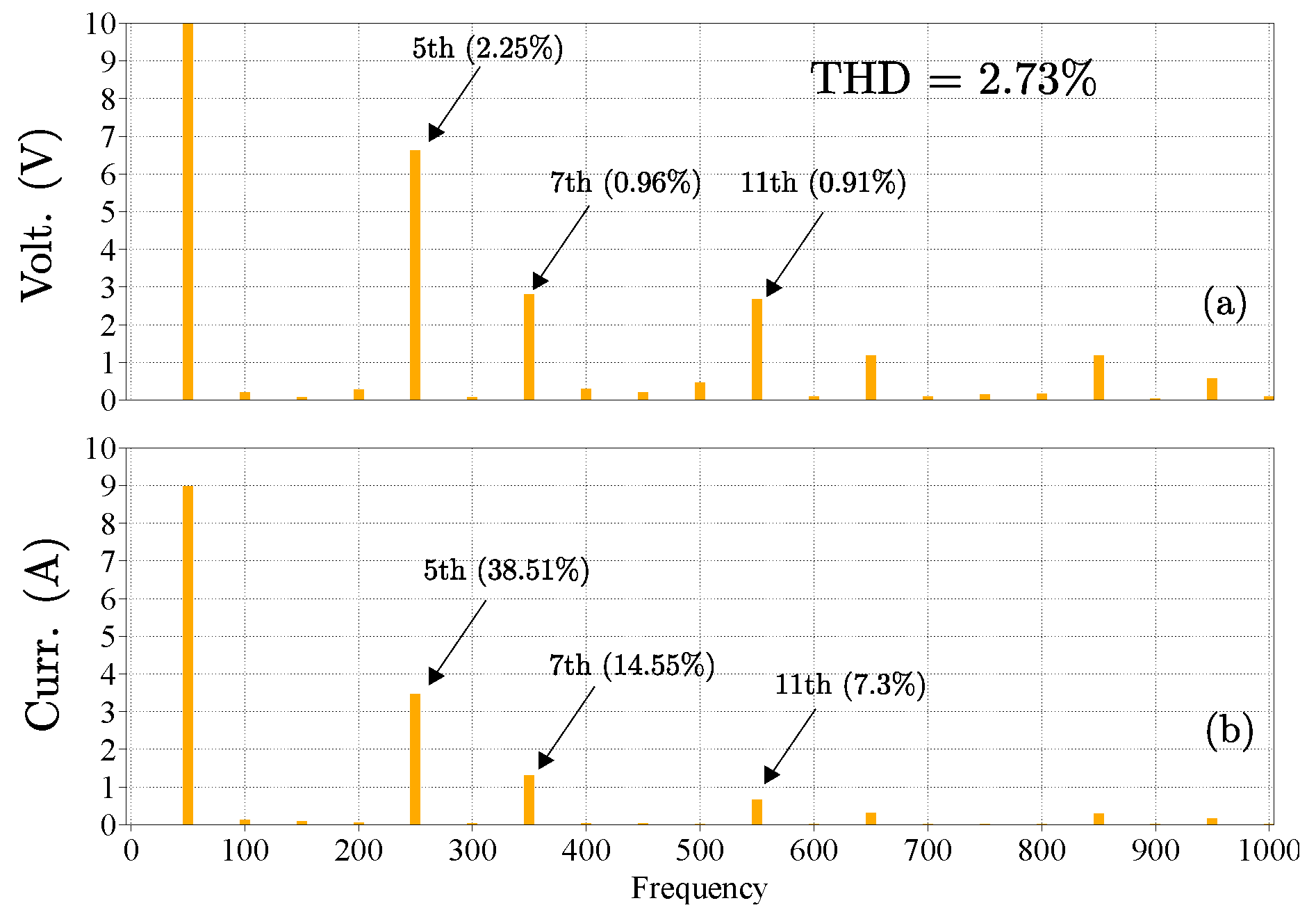
Preprints 93006 g008
Preprints 93006 g010
Figure 10. Transient operation of the system for a load step. (a) Load output voltage, and (b) Filter inductor current.
Figure 10. Transient operation of the system for a load step. (a) Load output voltage, and (b) Filter inductor current.
Preprints 93006 g010
Table 1. System Parameters.
Table 1. System Parameters.
Parameter Value
Switching and Sampling frequency f s = 20 [kHz]
DC-link voltage V d c = 700 V
LC Filter R f = 1 m Ω L f = 2.4 mH C f = 15 μ F
Load resistance R L = 30 Ω
Non-linear load L n = 1.8 mH C n = 2.2 mF R n = 60 Ω
Filter current weight factor λ i = 0.25
Load voltage weight factor λ v = 0.02
Control effort weight factor λ u = 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
An Optimal Switching Sequence Model Predictive Control Scheme for the 3L-NPC with Output LC Filter

Felipe Herrera

et al.

,

2023

Microgrids Power Quality Enhancement Using Model Predictive Control

Félix Garcia-Torres

et al.

,

2021

A Robust Control of Two-Stage Grid-Tied PV Systems Employing Integral Sliding Mode Theory

Abbas Kihal

et al.

,

2018

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated