The loads generated inside agricultural silos under static and dynamic conditions depend on the mechanical properties of the materials stored inside them. The silo calculation methodologies are based on these mechanical properties. Although it is known that moisture content greatly influences the values reached by these mechanical properties, just few studies have been conducted to determine them. The present work determines the angle of internal friction, the apparent cohesion, the dilatancy angle and the apparent specific weight of wheat when subjected to different moisture contents. Direct shear and oedometer assay devices were used. In addition, a climatic chamber was used to moisten the wheat samples used in this work. The moisture content applied to the samples ranged from 7.5% to 15.5%. From the different assays carried out it could be observed that the values of the angle of internal friction and apparent cohesion obtained from direct shear assays, as well as those related to the apparent specific weight obtained from oedometer assays were like those found in the literature. The apparent specific weight increased as moisture content increased, reaching a peak value at a moisture content of 13.4%, followed by a drop at a moisture content of 15.5%. The values here provided can be used in silo load calculations involving numerical methods.

Keywords:

Subject: Engineering - Architecture, Building and Construction

1. Introduction

The loads generated inside agricultural silos can be calculated using both classical and numerical methodologies. Classical theories are suitable for determining these loads under static conditions, being the Janssen formula [1] the world´s most widely used. However, numerical methods began to be applied to silo calculation in the 1970s [2] and, since then, they have experimented a great surge especially during the 21^st Century thanks to advances in computing [3,4,5,6,7,8,9,10,11,12]. With these techniques, it is possible to accurately predict dynamic loads occurred during both the filling and the emptying of silos, in addition to model the static conditions. Any case, with all these methodologies, it is necessary to consider different mechanical properties of the materials stored inside agricultural silos, such as the angle of internal friction, the apparent cohesion, the bulk density, or the Young´s modulus, among others. Values of these parameters can be found within the literature for both granular and powdered materials [13,14,15,16,17,18,19,20,21,22,23]. These data are referred to dry samples, i.e., materials with an ambient humidity. Nevertheless, it has been well known for a long time that these material properties, the loads as well as the type of flow they generate inside silos are greatly influenced by moisture content as shown in some works [13,24,25,26,27,28,29,30,31,32,33,34].

Notwithstanding the above, to date there are not many works reported at the literature focused on the study of the influence of humidity when intermediate liquid contents are considered. They are mainly referred to the pendular state but rarely to the funicular state [35,36,37]. Under humidity effects, capillary forces appear when water molecules are placed between the grains. Under these circumstances both, the cohesion and the friction of the material are affected [29,38,39]. The amount of liquid present in the granular medium allows the establishment of capillary bridges between the grains and it determines the pendular, funicular or capillary states. These liquid bridges and/or capillary bridges can be created or destroyed as a material passes from a dry state to a wet one, or vice versa. This affects the shear strength, the friction between particles, the lubricating role of water or the cohesive behavior of the material, among other factors [37,40,41,42,43,44,45].

The aim of the present work was to provide values of the following mechanical properties: the angle of internal friction, the apparent cohesion, the apparent specific weight and the dilatancy angle. The material tested was wheat subjected to different moisture contents. The results add to those already reported in the literature for the first three and provides the first information of this kind for the fourth. In addition, these values could be useful to study the mechanical behavior of wheat when its moisture content is varied.

2. Materials and Methods

The assays conducted were all performed at the Geotechnical Laboratory of the Centro Universitario de Plasencia (University of Extremadura). The material used in this work was wheat.

The properties determined for this material were: the angle of internal friction (ϕ), the apparent cohesion (C), the dilatancy angle (ψ) and the apparent specific weight (γ).

A description of the different assays carried out to determine the values or these parameters has been provided in detail elsewhere [21,22]. However, information regarding particular conditions is provided below.

2.1. Climatic chamber

Wheat samples were subjected to different moisture contents and temperatures by means of a climatic chamber available at the laboratory. The temperatures ranged from 20 °C to 55 °C, whereas the relative humidity ranged from 25% to 90%. Different combinations of temperature and relative humidity allowed to reach the desired humidity values in the samples used. Each combination of temperature and humidity was maintained for a minimum of 72 hours to achieve homogeneity of moisture content in the samples used before beginning the corresponding assays. Figure 1 shows the climatic chamber used in this work:

2.2. Determination of the moisture content

Wheat samples were dried in an oven at 105-110°C, adhering to Part 1 of Standard UNE-EN ISO 17892 [46]. Each of them was weighed every 24 hours until a constant weight was reached. An electronic balance with a precision of 0.01 kg was used. Figure 2 shows the electronic balances used for determining the moisture content of the samples (right) and the weight of the oedometric cell (left). This last one had a precision of 0.1 kg.

2.3. Direct shear assays

The assays conducted in this work adhered to the procedure established in part 10 of Standard UNE-EN ISO 17892 [47]. The parameters determined with this device were the angle of internal friction, the apparent cohesion and the dilatancy angle. The main characteristics of the semi-automatic direct shear test device were reported in earlier work [23]. In this research work the normal stresses applied to the wheat samples were 10, 20, 50, 100, 200 and 300 kPa. The assay speed was 0.4 mm/min. This speed was high enough to prevent the sample from losing humidity while the test was performed. The assay was replicated twice at each stress.

2.4. Oedometric assays

The oedometric assays were performed according to the procedure described in Part 5 of Standard UNE-EN ISO 17892 [48]. The parameter determined with this device was the apparent specific weight of the material. The main characteristics of this device were also provided in earlier work [23]. The assay modality carried out on this occasion was the abbreviated one. It consisted of conducting an automatic increase or a decrease in the load applied just when a maximum deformation of 0.1 mm was reached for three consecutive hours. In that case, primary consolidation is assumed to have occurred. Faster assays could be conducted this way compared to the traditional ones considering that the samples had specific humidity conditions. Normal stresses of 8, 16, 32, 64, 128 and 256 kPa were applied. All assays were performed in triplicate.

The apparent specific weight of the material could be obtained as follows: The amount of sample placed within the oedometric cell was weighed right before beginning the assay. As the cells used in these assays are standardized, their volume is known. The height of the sample within the corresponding oedometric cell could be measured every time with the help of a displacement transducer. This way, the volume occupied by the sample after each loading step could be calculated and so the apparent specific weight of the material could be determined. Figure 3 shows the procedure described:

3. Results

3.1. Moisture content

Wheat samples were subjected to different combinations of temperature and relative humidity within the climatic chamber. A small amount of sample was chosen to determine its moisture content prior to beginning the assays. The moisture content of the sample was determined by drying it at the oven, as described in the previous section. Thus, the real moisture content of the sample could be determined. Table 1 shows the different combinations of temperature and relative humidity and their corresponding real moisture content expressed as dry basis (d.b.).

From the previous table it can be seen that moisture content of wheat samples ranged from 7,5 to 15,5%. This range of values is within that reported in other works [13,28,49].

3.2. Direct shear assays

3.2.1. Angle of internal friction and apparent cohesion

Strain-strain curves showing the relationship between the shear stress and the horizontal displacement at six different normal stresses (10, 20, 50, 100, 200 and 300 kPa) are plotted at Figure 4 for the two replications carried out at moisture contents of 15.5% and 7.5% d.b., respectively:

As expected, the higher the normal stress applied, the higher the shear stress reached. The peak value obtained for the lateral stress at a normal stress of 300 kPa and a moisture content of 15.5% was 175 kPa, which was a 29% higher than that reached when a moisture content of 7.5% was applied (136 kPa). However, lower differences (6.8 and 8.6%, respectively) were observed when normal stresses of 200 and 100 kPa were applied at both moisture contents. It should be noted that, in this case, at lower normal stresses applied (10, 20 and 50 kPa), the highest value obtained for the shear stress was higher at lower moisture content. This difference was 2.7%, 5.6% and 8.1% at 50, 20 and 10 kPa, respectively. Nevertheless, this trend could not be confirmed at intermediate moisture contents (10, 10.5 and 13.4%, respectively), where at lower normal stresses, the lateral stress was higher as moisture content increased. Finally, the shape of the curves was like those shown in Figure 4 for samples assayed at moisture contents of 10, 10.5 and 13.4%, respectively.

The regression lines for the Mohr-Coulomb strength envelopes obtained in the assays conducted at the different normal stresses and moisture contents considered are shown in Figure 5. The slope of these lines provides the value of the angle of internal friction, whereas the intersection with the ordinate axis provides that of the apparent cohesion.

As it can be seen, the regression line formula corresponding to each of the moisture contents applied to wheat samples is provided next to the legend of the previous figure.

Table 2 shows the mean ± standard deviation results obtained for the angle of internal friction (f) and the apparent cohesion (C) from the direct shear assays conducted at the different moisture contents selected:

From the above table it could be seen that a moisture content of 15.5% returned the highest value for the angle of internal friction. Therefore, the greatest resistance to shearing was reached at the highest moisture content tested. As for the apparent cohesion, no great values were returned in all cases, decreasing this value as the moisture content increased.

When comparing the regression lines for the Mohr-Coulomb strength envelopes obtained at low (10, 20 and 50 kPa) and high normal stresses (100, 200 and 300 kPa) it could be observed that both curves intersect in one point at moisture contents of 7.5, 10.0 and 13.4%, as shown in Figure 6. Nevertheless, no intersection could be observed at normal stresses of 10.5 and 15.5%, as shown in Figure 7.

Obviously, the differences observed between the Mohr-Coulomb strength envelopes plotted in Figure 6 provided different values for the angle of internal friction and the apparent cohesion depending on the range of normal stresses applied (low or high). Table 3 shows the mean ± standard deviation for the internal angle of friction and the apparent cohesion at low and high normal stresses:

With respect to the results obtained at low normal stresses, tests conducted at the highest moisture content (15.5%) returned the greatest value for the internal angle of friction, whereas those conducted at the lowest moisture content (7.5%) provided the lowest value for this parameter. Any case, these values were of the same order at low normal stresses, with a difference of 3% between the extreme values obtained, except at 10.5% moisture content. The value obtained at 10.5% was significantly lower (21%) compared with that obtained at a moisture content of 10.0%. When analyzing the values obtained for this parameter when high normal stresses were applied it could be observed that, in general, the higher the moisture content of the samples, the higher the corresponding values for the internal angle of friction. Therefore, wheat samples offered greater resistance to shearing as moisture content increased. The only exception was the value recorded at 13.4%, which was like that obtained at 10.5% moisture content.

As for the apparent cohesion values, those obtained at low normal stresses were lower than those recorded at high normal stresses. The only exception was the value returned at high normal stresses at a moisture content of 15.5%, though in this case the standard deviation could not be neglected.

3.2.2. Dilatancy angle

Figure 8 shows the deformation curves obtained via direct shear assays at moisture contents of 13.4% (Figure 8a) and 7.5% (Figure 8b) at the different normal stresses applied (10, 20, 50, 100, 200 and 300 kPa). The vertical deformation (e_V), needed for determining the dilatancy angle, is plotted on the ordinate axis, whereas the horizontal displacement (e_H) is plotted on the abscissa. Each curve represents the mean values from the two repetitions.

The different repetitions at each moisture content returned similar results. Immediately after beginning the assay, an initial compression of the samples took place as the particles adjusted their positions. The shearing stress was reached once the resistance they offered to shear was exceeded, then causing the displacement of the particles as they were less imbricated. This displacement increased the height of the vessel they occupied inside the shear box depending on the normal stress applied in each case. Thus, for normal stresses up to 200 kPa it was easy to observe this behavior. However, at the highest normal stress applied (300 kPa) it was not always possible to return a positive dilatancy since the thrust of the sample was not able to overcome that vertical stress. As expected, the vertical deformation values and, therefore, the dilatancy angle values, were higher as normal stresses applied decreased because the particles are freer to move. This is the reason why the difference in the vertical deformation recorded at 300 kPa and 10 kPa is significant.

Table 4 shows the mean ± standard deviation for the dilatancy angles obtained under the different normal stresses tested.

At lower normal stresses (10, 20 and 50 kPa), the assays conducted at a moisture content of 10.0% returned the highest dilatancy angles with the maximum value (17.0°) recorded at 10 kPa. From these results it was not possible to obtain a correlation between the values of this parameter and the moisture content applied to the samples. For the different moisture contents assayed, the dilatancy angle values fell as the normal stress exerted increased, though some exceptions occurred, such as those obtained at 10.0% and 10.5% moisture contents (4.7° and 1.2°, respectively) under a normal stress of 300 kPa, and that recorded at 13.4% moisture content at a normal stress of 200 kPa (8.3°).

When analyzing the fall of the dilatancy angles when comparing the highest and the lowest values recorded at each moisture content assayed, the greatest percentage change was registered at 10.5% moisture content (99%) between the minimum value (0.1°) and the maximum one (14.8°). This percentage change was 95% at 13.4% and 15.5% moisture contents, it achieved a value of 88% at 10.0% moisture content and the smallest percentage change (80%) was registered at 7.5% moisture content (the minimum value was 2.8° and the maximum one 14.2°).

3.3. Oedometric assays

Figure 9 shows the curves obtained from the oedometric assays carried out for determining the change in apparent specific weight of the material with changing the normal stress applied. As shown below, the normal stress applied (s) is plotted on the abscissa, whereas the apparent specific weight (g) is plotted on the ordinate axis. In this type of assays, the moisture contents applied to wheat samples were the same selected for the direct shear tests, i.e., 7.5, 10.0, 10.5, 13.4% and 15.5% (d.b.), respectively.

The curves plotted on the previous figure correspond to the mean values obtained from the three repetitions carried out with wheat samples at each of the moisture contents applied. The general trend was that the higher the moisture content of the sample, the higher the value of the apparent specific weight recorded except for the assays conducted at a moisture content of 15.5% since the corresponding curve is below that of 13.4%. As it was expected, in all cases the peak value obtained for this parameter was achieved at the highest normal stress applied (256 kPa). Finally, during the unloading cycle the slope of the curves is quite similar, with a slight and progressive fall in the values of this parameter as the normal stress applied decreased, too. This trend was also followed but not so clear as for the remaining cases at a moisture content of 15.5%.

Curves plotted in Figure 10 show the change in apparent specific weight with the moisture content under the different normal stresses applied. The apparent specific weight is plotted on the ordinate axis, whereas the moisture content is plotted on the abscissa.

The higher the normal stress applied to the samples, the higher the values of the apparent specific weight achieved. The shape of these curves was like that obtained in Proctor compaction tests with soils to determine the maximum density that a particular type of soil can be compacted to at an optimum water content.

Table 5 shows the mean ± standard deviation for the apparent specific weight values obtained under the different normal stresses and moisture contents tested.

Assays conducted at a moisture content of 13.4% returned the highest apparent specific weight, with values always close to 8.0 kN/m³. At this humidity, the apparent specific weight increased by some 9% at the highest normal stress compared to 0 kPa. However, this percentage fluctuated around 6% at moisture content of 15.5%, around 5% at moisture contents of 10.0 and 10.5% and around 3% at a moisture content of 7.5%.

4. Discussion

4.1. Moisture content

The moisture contents selected in this work were within the range reported by other authors [13,34,49,50]. Therefore, the results provided from the assays conducted can be discussed with those found in the literature in case they exist.

4.2. Direct shear assays

4.2.1. Angle of internal friction and apparent cohesion

The shape of the curves obtained when the shear stress is plotted vs. the horizontal displacement is like those reported in previous works for other granular agricultural materials [20,23]. When comparing the results here obtained for the internal angle of friction with those reported by Moya et al. [23] under ambient humidity (9.76% moisture content) using the same material in both works, the minimum value recorded (22.9°) at a moisture content of 7.5% was 16% higher than that recommended in that work. In addition, this minimum value was up to 36% higher than that reported when triaxial assays were conducted at 10% axial deformation. However, the value provided for this parameter at 10.0% moisture content (24.9°) was 3.7% higher than that recorded by these authors from direct shear assays (24.0°). Any case, the range of values lies over those reported by some authors, with values from 5% to 12% smaller [13,14,22,51], to around 10% to 16% higher [19,20,21]. Similar differences were found for the range of values returned at low and high normal stress levels.

The differences might be attributed to differences in the moisture content, the arrangement of the particles, the bulk density, the orientation of the particles within the shear box, the formation of shear bands, the consolidation time (in some of those works cited samples were previously consolidated) and the shape of the particles [13].

As commented, the wheat sample used in this work was the same assayed at Moya et al. [23] under ambient humidity. The values obtained for the apparent cohesion lies over the range of values reported by these authors. On the other hand, the values here provided were notably higher than those reported in other works [13,19,20,22] considering that they ranged between 6.47 and 12.50 kPa, which were not too high values. Similar differences were found for the values obtained for this parameter at low normal stresses, whereas at high normal stresses the maximum value (19.11 kPa) increased its difference with respect to those reported in the referred literature.

4.2.2. Dilatancy angle

The range of dilatancy angle values lies within that reported in the literature by some authors [19,20,21,22,23,52,53]. It was not possible to find within the literature information related to the influence of moisture content on this parameter since all documents accessed were referred to dry samples, i.e. under ambient humidity. The general trend showed that the dilatancy angle decreases as the normal stress raises, confirming that stated by Zeng et al. [53].

4.3. Oedometric assays

The apparent specific weight values ranged from 7.35 to 8.02 kN/m³, which lied over those reported in numerous studies within the literature [14,15,17,20,21,22,23,34,54,55,56], although is 3% smaller than those reported in other works [57,58] and 6% higher than the minimum value provided in other one [13]. In this latter case, the values provided by authors varied between 6.94 and 7.73 kN/m³, depending on the moisture content applied. In fact, that minimum value reported corresponded to a moisture content of 15.0%, whereas those corresponding to moisture contents of 10.0% and 12.5% achieved 7.73 kN/m³ and 7.65 kN/m³, respectively, i.e., they were within the range of values here recorded from the assays conducted.

Higher apparent specific weight values were returned as moisture content increased from 7.5 to 13.4%, then decreasing at a moisture content of 15.5%. This was not expected according to that reported in some studies [49,59,60,61], who stated that bulk density decreased with an increase in moisture content. Moreover, some numerical models have been developed to predict the decrease of bulk density as moisture content increased [50,62]. These studies consider that wheat is more compressible at higher moisture content than at lower moisture content [63]. Despite of this, some studies have reported values of bulk density as moisture dependent showing a similar tendency to that provided in this work, with values increasing up to a moisture content of 13.3% and decreasing at higher moisture contents [34] and with values at 17.5 and 20.0% moisture contents higher than those obtained at 15% moisture content [13]. Maybe the presence of water could affect the orientation and the arrangement of the particles in the oedometer cells.

5. Conclusions

From the direct shear assays, it could be checked that the values of the internal angle of friction lied over those reported in the literature. Nevertheless, the apparent cohesion values obtained here were not too high, although they were mostly higher than those found in the literature.

The range of dilatancy angle values was within that reported in the literature. It could be confirmed that, as general trend, the values of this parameter decreased as the normal stress applied raised.

In general, the apparent specific weight values recorded were similar or very close to those reported in the literature. The values of this parameter increased up to a moisture content of 13.4%, then decreasing at higher moisture contents. This trend was inconsistent with what was observed and modeled in other works, although it coincided with what was published in some other works.

Author Contributions

Conceptualization, M.M.; methodology, M.M. and J.R.V.; software, M.M.; validation, M.M., J.R.V., D.S. and J.A.R.; formal analysis, M.M., D.S. and J.A.R.; investigation, M.M., J.R.V., D.S. and J.A.R.; data curation, M.M., D.S. and J.A.R.; writing—original draft preparation, M.M.; writing—review and editing, M.M., J.R.V., D.S. and J.A.R.; supervision, M.M., J.R.V., D.S. and J.A.R.; funding acquisition, M.M. and J.R.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research and APC was funded by the Spanish “Agencia Estatal de Investigación” via the research project “Study of the structural behavior of corrugated wall silos using Discrete Element Models (SILODEM)”, grant number PID2019-107051GB-I00/AEI/10.13039/501100011033.

Data Availability Statement

Not applicable.

Acknowledgments

The authors thank Leonesa Astur de Piensos, S.A. (LESA) company for providing the wheat used in this research.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

Janssen, H. Versuche Über Getreidebruck in Silozellen. Zeitschrift des Vereines deutscher Ingenieure 1895, 1045–1049. [Google Scholar]
Jofriet, J.C.; Lelievre, B.; Fwa, T.F. Friction Model for Finite Element Analyses of Silos. Transactions of the American Society of Agricultural Engineers 1977, 735–740. [Google Scholar] [CrossRef]
Ayuga, F.; Guaita, M.; Aguado, P. Static and Dynamic Silo Loads Using Finite Element Models. Journal of Agricultural and Engineering Research 2001, 78, 299–308. [Google Scholar] [CrossRef]
Patwa, A.; Ambrose, R.P.K.; Casada, M.E. Discrete Element Method as an Approach to Model the Wheat Milling Process. Powder Technol 2016, 302, 350–356. [Google Scholar] [CrossRef]
Ai, J.; Chen, J.F.; Rotter, J.M.; Ooi, J.Y. Finite Element Prediction of Progressively Formed Conical Stockpiles. 1–13.
Wang, Y.; Lu, Y.; Ooi, J.Y. A Numerical Study of Wall Pressure and Granular Flow in a Flat-Bottomed Silo. Powder Technol 2015, 282, 43–54. [Google Scholar] [CrossRef]
Rotter, J.M.; Holst, J.M.F.G.; Ooi, J.Y.; Sanad, A.M. Silo Pressure Predictions Using Discrete-Element and Finite-Element Analyses. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 1998, 356, 2685–2712. [Google Scholar] [CrossRef]
Kobyłka, R.; Molenda, M.; Horabik, J. Loads on Grain Silo Insert Discs, Cones, and Cylinders: Experiment and DEM Analysis. Powder Technol 2019, 343, 521–532. [Google Scholar] [CrossRef]
Madrid, M.A.; Fuentes, J.M.; Ayuga, F.; Gallego, E. Determination of the Angle of Repose and Coefficient of Rolling Friction for Wood Pellets. Agronomy 2022, 12. [Google Scholar] [CrossRef]
González-Montellano, C.; Gallego, E.; Ramírez-Gómez, Á.; Ayuga, F. Three Dimensional Discrete Element Models for Simulating the Filling and Emptying of Silos: Analysis of Numerical Results. Comput Chem Eng 2012, 40, 22–32. [Google Scholar] [CrossRef]
Briassoulis, D. Finite Element Analysis of a Cylindrical Silo Shell under Unsymmetrical Pressure Distributions. Comput Struct 2000, 78, 271–281. [Google Scholar] [CrossRef]
Horabik, J.; Parafiniuk, P.; Molenda, M. Stress Profile in Bulk of Seeds in a Shallow Model Silo as Influenced by Mobilisation of Particle-Particle and Particle-Wall Friction: Experiments and DEM Simulations. Powder Technol 2018, 327, 320–334. [Google Scholar] [CrossRef]
Molenda, M.; Horabik, J. Mechanical Properties of Granular Agro-Materials and Food Powders for Industrial Practice. Part I: Characterization of Mechanical Properties of Particulate Solids for Storage and Handling; Horabik, J., Laskowski, J., Eds.; Institute of Agrophysics Polish Academy of Science: Lublin (Poland), 2005. [Google Scholar]
Lebègue, Y.; Boudakian, A. Bases Des Règles « Silos » Du SNBATI—Essais Sur Les Produits et Principes Des Formules « Silos ». Ann. ITBTP 1989, 69–113. [Google Scholar]
Bucklin, R.A.; Molenda, M.; Bridges, T.C.; Ross, I.J. Slip-Stick Frictional Behavior of Wheat on Galvanized Steel. Transactions of the American Society of Agricultural Engineers 1996, 39, 649–653. [Google Scholar] [CrossRef]
Bucklin, R.A.; Thompson, S.A.; Ross, I.J.; Biggs, R.H. Apparent Dynamic Coefficient of Friction of Corn on Galvanized Steel Bin Wall Material. Transactions of the American Society of Agricultural Engineers 1993, 36, 1915–1918. [Google Scholar] [CrossRef]
Thompson, S.A.; Bucklin, R.A.; Batich, C.D.; Ross, I.J. Variation in the Apparent Coefficient of Friction of Wheat on Galvanized Steel. Transactions of the ASAE 1988, 31, 1518–1524. [Google Scholar] [CrossRef]
Ramírez, A.; Moya, M.; Ayuga, F. Determination of the Mechanical Properties of Powdered Agricultural Products and Sugar. Particle and Particle Systems Characterization 2010, 26, 220–230. [Google Scholar] [CrossRef]
Molenda, M.; Stasiak, M.; Moya, M.; Ramirez, A.; Horabik, J.; Ayuga, F. Testing Mechanical Properties of Food Powders in Two Laboratories - Degree of Consistency of Results. Int Agrophys 2006, 20, 37–45. [Google Scholar]
Moya, M.; Aguado, P.J.; Ayuga, F. Mechanical Properties of Some Granular Agricultural Materials Used in Silo Design. Int Agrophys 2013, 27, 181–193. [Google Scholar] [CrossRef]
Moya, M.; Ayuga, F.; Guaita, M.; Aguado, P.J. Mechanical Properties of Granular Agricultural Materials. Transactions of the ASAE 2002, 45, 1569–1577. [Google Scholar] [CrossRef]
Moya, M.; Guaita, M.; Aguado, P.; Ayuga, F. Mechanical Properties of Granular Agricultural Materials, Part 2. Trans ASABE 2006, 49, 479–489. [Google Scholar] [CrossRef]
Moya, M.; Sánchez, D.; Villar-García, J.R. Values for the Mechanical Properties of Wheat, Maize and Wood Pellets for Use in Silo Load Calculations Involving Numerical Methods. Agronomy 2022, 12. [Google Scholar] [CrossRef]
Kibar, H.; Öztürk, T.; Esen, B. The Effect of Moisture Content on Physical and Mechanical Properties of Rice (Oryza Sativa L.). Spanish Journal of Agricultural Research 2010, 8, 741–749. [Google Scholar] [CrossRef]
Mattsson, J.E.; Kofman, P.D. Influence of Particle Size and Moisture Content on Tendency to Bridge in Biofuels Made from Willow Shoots. Biomass Bioenergy 2003, 24, 429–435. [Google Scholar] [CrossRef]
Ponce-García, N.; Ramírez-Wong, B.; Torres-Chávez, P.I.; De Dios Figueroa-Cárdenas, J.; Serna-Saldívar, S.O.; Cortez-Rocha, M.O. Effect of Moisture Content on the Viscoelastic Properties of Individual Wheat Kernels Evaluated by the Uniaxial Compression Test under Small Strain. Cereal Chem 2013, 90, 558–563. [Google Scholar] [CrossRef]
Brar, H.S.; Sidhu, G.K.; Singh, A. Effect of Moisture Content on Engineering Properties of Oats (Avena Sativa L.). Agricultural Engineering International: CIGR Journal 2016, 18, 186–193. [Google Scholar]
Zaalouk, A.K.; Zabady, F.I. Effect of Moisture Content on Angle of Repose and Friction Coefficient of Wheat Grain. Misr Journal of Agricultural Engineering 2009, 26, 418–427. [Google Scholar] [CrossRef]
Davies, R.M.; El-Okene, A.M. Moisture-Dependent Physical Properties of Soybeans. Int Agrophys 2009, 23, 299–303. [Google Scholar]
Lancaster, J.K. A Review of the Influence of Environmental Humidity and Water on Friction, Lubrication and Wear. Tribol Int 1990, 23, 371–389. [Google Scholar] [CrossRef]
Wiacek, J.; Molenda, M. Moisture-Dependent Physical Properties of Rapeseed - Experimental and DEM Modeling. Int Agrophys 2011, 25, 59–65. [Google Scholar]
Wandkar, S.V.; Ukey, P.D.; Pawar, D.A. Determination of Physical Properties of Soybean at Different Moisture Levels. Agricultural Engineering International: CIGR Journal 2012, 14, 138–142. [Google Scholar]
Teunou, E.; Fitzpatrick, J.J. Effect of Relative Humidity and Temperature on Food Powder Flowability. J Food Eng 1999, 42, 109–116. [Google Scholar] [CrossRef]
Cheng, X.; Zhang, Q.; Shi, C.; Yan, X. Model for the Prediction of Grain Density and Pressure Distribution in Hopper-Bottom Silos. Biosyst Eng 2017, 163, 159–166. [Google Scholar] [CrossRef]
Gorji, A.; Rajabipour, A.; Tavakoli, H. Fracture Resistance of Wheat Grain as a Function of Moisture Content, Loading Rate and Grain Orientation. Aust J Crop Sci 2010, 4, 448–452. [Google Scholar]
Landi, G.; Barletta, D.; Poletto, M. Modelling and Experiments on the Effect of Air Humidity on the Flow Properties of Glass Powders. Powder Technol 2011, 207, 437–443. [Google Scholar] [CrossRef]
Louati, H.; Oulahna, D.; de Ryck, A. Effect of the Particle Size and the Liquid Content on the Shear Behaviour of Wet Granular Material. Powder Technol 2017, 315, 398–409. [Google Scholar] [CrossRef]
Frye, K.M.; Marone, C. Effect of Humidity on Granular Friction at Room Temperature. J Geophys Res Solid Earth 2002, 107, ETG 11-1–ETG 11-13. [Google Scholar] [CrossRef]
Nokhodchi, A. An Overview of the Effect of Moisture on Compaction and Compression. Pharmaceutical Technology 2005, 29, 46–66. [Google Scholar]
Delenne, J.Y.; Soulié, F.; El Youssoufi, M.S.; Radjai, F. From Liquid to Solid Bonding in Cohesive Granular Media. Mechanics of Materials 2011, 43, 529–537. [Google Scholar] [CrossRef]
Delenne, J.; El Youssoufi, M.; Cherblanc, F.; Bénet, J. Mechanical Behavior and Failure of Cohesive Granular Materials. Int J Numer Anal Methods Geomech 2004, 1577–1594. [Google Scholar] [CrossRef]
Jiang, M.J.; Yu, H.S.; Harris, D. Bond Rolling Resistance and Its Effect on Yielding of Bonded Granulates by DEM Analyses. Int J Numer Anal Methods Geomech 2006, 30, 723–761. [Google Scholar] [CrossRef]
Louati, H.; Oulahna, D.; de Ryck, A. Apparent Friction and Cohesion of a Partially Wet Granular Material in Steady-State Shear. Powder Technol 2015, 278, 65–71. [Google Scholar] [CrossRef]
Richefeu, V.; Youssoufi, M.S. El; Radjaï, F. Shear Strength of Unsaturated Soils: Experiments, DEM Simulations, and Micromechanical Analysis. In Theoretical and Numerical Unsaturated Soil Mechanics; Springer Berlin Heidelberg, 2007; pp. 83–91.
Richefeu, V.; Saïd, M.; Youssoufi, E.; Radjai, F.; Farhang, R.; Sa¨ıd, M.; Youssoufi, S. El; Radja¨ı, F.R. Shear Strength Properties of Wet Granular Materials. Phys Rev E Stat Nonlin Soft Matter Phys 2006, 73. [Google Scholar] [CrossRef] [PubMed]
UNE-EN ISO 17892-1 Geotechnical Investigation and Testing. Laboratory Testing of Soil. Part 1: Determination of Water Content. 2015.
UNE-EN ISO 17892-10 Geotechnical Investigation and Testing. Laboratory Testing of Soil. Part 10: Direct Shear Tests 2018.
UNE-EN ISO 17892-5 Geotechnical Investigation and Testing. Laboratory Testing of Soil. Part 5: Incremental Loading Oedometer Test 2017.
Tabatabaeefar, A. Moisture-Dependent Physical Properties of Wheat. Int Agrophys 2003, 17, 207–211. [Google Scholar]
Gao, M.; Cheng, X.; Du, X. Simulation of Bulk Density Distribution of Wheat in Silos by Finite Element Analysis. J Stored Prod Res 2018, 77, 1–8. [Google Scholar] [CrossRef]
Moysey, E.; Lambert, E.; Wang, Z. Flow Rates of Grains and Oilseeds through Sharp-Edged Orifices. Transactions of the American Society of Agricultural Engineers 1988, 31, 226–231. [Google Scholar] [CrossRef]
Zeng, C.; Wang, Y. The Shear Strength and Dilatancy Behavior of Wheat Stored in Silos. Complexity 2019, 2019. [Google Scholar] [CrossRef]
Zeng, C.; Gu, H.; Wang, Y. Stress-Strain Response of Sheared Wheat Granular Material Stored in Silos Using Triaxial Compression Tests. Int Agrophys 2020, 34, 103–114. [Google Scholar] [CrossRef]
Zhang, Q.; Britton, M.G. A Micromechanics Model for Predicting Dynamic Loads during Discharge in Bulk Solids Storage Structures. Canadian Biosystems Engineering / Le Genie des biosystems au Canada 2003, 45, 5.21–5.27. [Google Scholar]
Zhang, Q.; Li, Y.; Puri, V.M.; Manbeck, H.B. Physical Properties Effect on Stress-Strain Behavior of Wheat En Masse - Part II. Constitutive Elastoplastic Parameter Dependence on Initial Bulk Density and Moisture Content. Transactions of the American Society of Agricultural Engineers 1989, 32, 203–209. [Google Scholar] [CrossRef]
Reimbert, M.; Reimbert, A. Silos.Theory and Practice; Lavoisier, 1987; ISBN 9782852063655.
Zeng, C.; Wang, Y. Compressive Behaviour of Wheat from Confined Uniaxial Compression Tests. Int Agrophys 2019, 33, 347–354. [Google Scholar] [CrossRef]
R. N. Sinha; W.E. Muir Grain Storage: Part of a, System, Sinha, R.N., Muir, W.E., Eds.; Avi Publishing Company: Wisconsin - Madison, 1973. [Google Scholar]
Carman, K. Some Physical Properties of Lentil Seeds. J. agric. Engng Res 1996, 63, 87–92. [Google Scholar] [CrossRef]
Dutta, S.K.; Nema, ; V K; Bhardwaj, ; R K Physical Properties of Gram; 1988; Vol. 39.
Shepherd·, H.; Bhardwaj·, ; R K Moisture-Dependent Physical Properties of Pigeon Pea; 1986; Vol. 35.
Turner, A.P.; Montross, M.D.; McNeill, S.G.; Sama, M.P.; Casada, M.C.; Boac, J.M.; Bhadra, R.E.; Maghirang, R.G.; Thompson, S.A. Modeling the Compressibility Behavior of Hard Red Wheat Varieties. Trans ASABE 2016, 59, 1029–1038. [Google Scholar]
Thompson, S.A.; Ross, I.J. Compressibility and Frictional Coefficients of Wheat. Transactions of the ASAE 1983, 26, 1171–1176. [Google Scholar] [CrossRef]

Figure 1. Climatic chamber device.

Figure 2. Electronic balances used in this work.

Figure 3. Scheme of the oedometric assay conducted to determine the apparent specific weight.

Figure 4. Stress-strain curves obtained for wheat samples at normal stresses of 10, 50 and 200 kPa for the two replications conducted at moisture contents of 15.5% (a) and 7.5% (b), respectively.

Figure 5. Regression lines for the Mohr-Coulomb strength envelopes obtained from direct shear assays conducted at different moisture contents.

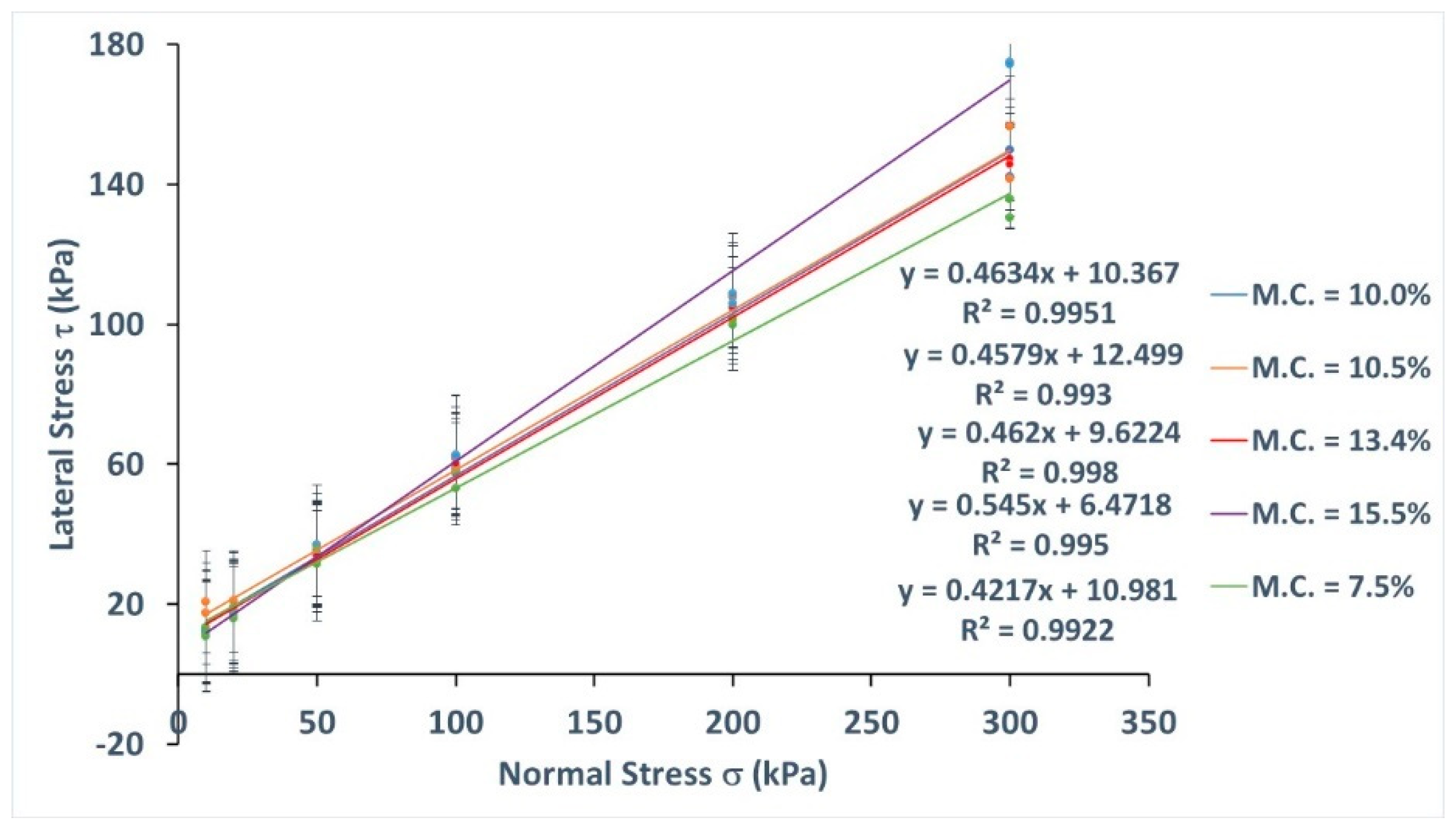
Figure 6. Regression lines for the Mohr-Coulomb strength envelopes obtained from direct shear assays conducted at low (10, 20 and 50 kPa) and high (100, 200 and 300 kPa) normal stresses and moisture contents of 13.4% (a) and 10.0% (b), respectively.

Figure 7. Regression lines for the Mohr-Coulomb strength envelopes obtained from direct shear assays conducted at low (10, 20 and 50 kPa) and high (100, 200 and 300 kPa) normal stresses and moisture contents of 15.5% (a) and 10.5% (b), respectively.

Figure 8. Deformation curves for wheat samples at (a) 13.4% moisture content and (b) 7.5% moisture content.

Figure 9. Variation of the apparent specific weight with the normal stress at different moisture contents.

Figure 10. Variation of the apparent specific weight with the moisture content at different normal stresses applied.

Table 1. Combinations of temperature and relative humidity used in this work and their corresponding real moisture content (d.b.) determined by drying the samples in an oven at 105-110°C.

Climatic chamber conditions		Moisture content (d.b.) (%)
Temperature (°C)	Relative humidity (%)	Moisture content (d.b.) (%)
55	25	7.5
20	35	10
20	45	10.5
20	65	13.4
20	90	15.5

Table 2. Mean ± standard deviation for the angle of internal friction and the apparent cohesion at the different moisture contents assayed.

Moisture content (%) (d.b.)	Angle of internal friction (f)	Apparent cohesion (C, kPa)
7.5	22.9° ± 0.6	10.98 ± 1.82
10.0	24.9° ± 0.5	10.37 ± 1.59
10.5	24.6° ± 0.6	12.50 ± 1.88
13.4	24.8° ± 0.3	9.62 ± 1.01
15.5	28.6° ± 0.5	6.47± 1.88

Table 3. Mean ± standard deviation for the internal angle of friction and the apparent cohesion at the different moisture contents tested (d.b.) for ranges of low (10, 20 and 50 kPa) and high (100, 200 and 300 kPa) normal stresses.

Moisture Content (%) (d.b.)	Angle of internal friction (f)		Apparent cohesion (C, kPa)
Moisture Content (%) (d.b.)	Low normal stresses	High normal stresses	Low normal stresses	High normal stresses
7.5	28.2° ± 2.2	21.2° ± 1.1	6.81 ± 1.56	18.98 ± 4.88
10.0	29.0° ± 0.7	23.1° ± 0.8	6.66 ± 0.53	19.11 ± 3.76
10.5	22.9° ± 4.0	23.9° ± 1.4	12.83 ± 2.61	15.88 ± 6.26
13.4	29.0° ± 0.4	23.7° ± 0.4	6.37 ± 0.26	15.18 ± 1.81
15.5	29.2° ± 1.7	29.3° ± 1.4	6.71 ± 1.20	2.74± 7.06

Table 4. Mean ± standard deviation for the dilatancy angle under the normal stresses assayed.

Normal stress (kPa)	Dilatancy angle (Y)
	Moisture content (d.b.)
	7.5%	10.0%	10.5%	13.4%	15.5%
10	14.2° ± 1.4	17.0° ± 2.2	14.8° ± 2.0	15.3° ± 1.2	12.4° ± 2.6
20	11.6° ± 1.1	15.9° ± 3.8	13.4° ± 1.6	13.2° ± 1.0	8.5° ± 0.1
50	6.5° ± 2.2	8.0° ± 5.7	7.3° ± 0.1	8.2° ± 5.4	8.5° ± 2.3
100	3.6° ± 2.1	5.5° ± 4.0	5.9° ± 0.2	3.6° ± 5.0	7.4° ± 0.6
200	7.0° ± 2.0	2.1° ± 2.9	0.1° ± 0.0	8.3°± 2.1	3.9°± 2.6
300	2.8° ± 0.8	4.7° ± 1.4	1.2° ± 1.5	0.8° ± 0.9	0.8° ± 1.0

Table 5. Mean ± standard deviation for the dilatancy angle under the normal stresses assayed.

Normal stress (kPa)	Apparent specific weight (g) (kN/m3)
	Moisture content
	7.5%	10.0%	10.5%	13.4%	15.5%
0	7.36 ± 0.00	7.37 ± 0.00	7.35 ± 0.00	7.35 ± 0.00	7.36 ± 0.00
8	7.38 ± 0.00	7.41 ± 0.02	7.42 ± 0.02	7.50 ± 0.01	7.41 ± 0.01
16	7.39 ± 0.01	7.45 ± 0.02	7.46 ± 0.02	7.59 ± 0.02	7.46 ± 0.01
32	7.43 ± 0.01	7.51 ± 0.03	7.52 ± 0.02	7.70 ± 0.02	7.53 ± 0.00
64	7.47 ± 0.01	7.58 ± 0.04	7.58 ± 0.02	7.78± 0.02	7.62 ± 0.02
128	7.53 ± 0.02	7.66 ± 0.04	7.65 ± 0.02	7.88 ± 0.02	7.73 ± 0.05
256	7.61 ± 0.04	7.75 ± 0.06	7.75 ± 0.02	8.02 ± 0.04	7.81 ± 0.06
128	7.59 ± 0.03	7.75 ± 0.06	7.73 ± 0.02	8.01 ± 0.03	7.81 ± 0.06
64	7.58 ± 0.03	7.74 ± 0.06	7.72 ± 0.02	8.00 ± 0.02	7.81 ± 0.06
32	7.55 ± 0.01	7.72 ± 0.07	7.70 ± 0.02	7.99 ± 0.02	7.81 ± 0.06
16	7.55 ± 0.02	7.71 ± 0.07	7.69 ± 0.01	7.98 ± 0.01	7.80 ± 0.07
8	7.55 ± 0.02	7.70 ± 0.07	7.68 ± 0.01	7.98 ± 0.01	7.80 ± 0.07

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Influence of Moisture Content on Some Mechanical Properties of Wheat

Abstract