Prerpints.org logo
Preprint
Article

Determination of Variable Humidity Profile for Lactic Acid Maximization in Fungal Solid-State Fermentation

Altmetrics

Downloads

84

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 March 2024

Posted:

22 March 2024

You are already at the latest version

Alerts
Abstract
Solid-state fermentation (SSF) is the bioprocess where microorganisms are cultivated in the absence of free water under control conditions. Lactic acid can be produced by fermenting grape stalks with Rhizopus oryzae in SSF. During the microorganism growth, the temperature and water content of the solid bed fluctuate, leading to areas of either dry or excessive moisture in the solid substrate. Therefore, it's crucial to control the supply of water to the matrix. In this work, we obtain lactic acid through SSF of grape stalks using Rhizopus oryzae NCIM 1299. The SSF was conducted at a fixed temperature of 35 °C, with three constant relative humidity levels: 50, 65, and 80 %RH. Mathematical models, including the Logistic and First Order Plus Dead Time models for fungal biomass growth and the Luedeking and Piret with Delay Time model for lactic acid production, were adjusted to kinetic curves. Growth kinetic parameters (Xmax, μmax, Tp, T0, Yp/x and td) were determined for all conditions. These kinetic parameters were then correlated with relative humidity using a second-degree polynomial relationship. We observed a decrease in Xmax with increasing %RH, while the value of Yp/x increased at higher %RH. Finally, the optimal variable relative humidity profile was obtained by applying the Dynamic Optimization Technique, resulting in a 15.30% increase in lactic acid production.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

The transition towards an eco-friendly world has been a topic of discussion for many years. However, efficient strategies must be implemented for a sustainable planet to become a reality in the short term. Based on this, the bioeconomy suggests the development of green technologies for a sustainable production of bioproducts from agricultural wastes, emerging as a sustainable alternative to traditional linear production [1]. Agricultural wastes are the residues from the growing and processing of raw material such as fruits, vegetables, meat, poultry, dairy products and crops [2]. They can be solid, liquid or slurries and their characteristics define the type of processing to be applied: energy production (by incineration), composting, animal feed, extraction of added value compound (bio-compounds) or inoculation with appropriate microorganisms (bacteria, yeasts or fungi) to obtain metabolite by biotransformation [3].
As can be observed, from the vast majority of alternatives that can be applied to the valorization of agro-industrial waste, bioprocesses are part of a promising, profitable, and viable alternative to obtain a wide variety of biobased products. The development of biobased products promotes a sustainable economy without dependence on petrochemical-derived fuels, representing an estimated market volume of USD 429.5 billion in 2024, with a compound annual growth rate (CAGR) of 6.96% (2024-2029) [4]. Despite the growth trend of this market, it is considered that it has not yet taken off due to the difficulty in: obtaining affordable and sustainable raw materials from reliable sources, ensuring good yields at larger scales, and having a concrete demand from consumers [5]. Therefore, biotechnological advances are crucial to reducing production costs, improving yields, and making this market attractive to future investors.
A significant contribution that would enhance the biotechnological advances is the implementation of optimization and control strategies for bioprocesses. Process control is a necessary tool to ensure the stability of any system, including bioprocesses, as they are regulated by a complex interaction between the physical, chemical, and biological conditions of the fermentation environment and the biochemical processes that occur within microorganisms [6]. Bioprocesses can take place in liquid phase (submerged fermentation, SmF) or solid phase (Solid State Fermentation, SSF), with SmF being more widely used because different large-scale operations are easier to carry out in liquids: such as pumping, sterilization and parameter control [7]. However, SSF has advantages that make it a tempting bioprocess: the use of a small amount of water in the process and high metabolite volumetric productivity [8].
Lactic acid (LA) is one of the few biobased organic acids that can be produced by fungal SSF from different inexpensive agricultural residues and food waste, such as sugarcane bagasse and juice, corn grain, among others [9]. Since a few years ago, various biotech companies have been actively investing in the commercialization of bio-based LA, such as: NatureWorks LLC (United States), Corbion-Purac (The Netherlands) and Galactic S.S (Belgium). The most significant demands for LA in the global market come from the food industry, cosmetics, and pharmaceuticals, having gained great importance in recent years its use as a precursor of the biopolymer polylactic acid (PLA), and also its use as a fundamental part of Natural Deep Eutectic Solvents (NADES) being a type of green solvents [10].
The performance of SSF can be affected by biological factors (type of microorganism, inoculum concentration, type solid substrate type), physicochemical factors (moisture content of the solid bed, pH, temperature, aeration, particle size, gas composition), and mechanical factors (application or absence of mixing and type of bioreactor employed) [11]. Based on this, it is necessary to ensure that the temperature and moisture of the solid bed are maintained within an operational range that favors the growth of the microorganism and the production of the bioproduct [12].
Temperature and relative humidity (or moisture of solid substrate) tend to fluctuate significantly in SSF due to the heterogeneity present in the system (characterized by the existence of gas phase, low moisture phase and agro-industrial solid). This complexity adds difficulty to the phenomena of heat and matter transfer, resulting in localized temperature increases and humidity decreases (due to water evaporation and microbial consumption), which negatively influences the growth of the microorganism and the productivity of the bioproduct [13]. Therefore, matrix water supply should be controlled.
In SSF bioreactors, it is most common to control the conditions of the inlet air, including flow rate, relative humidity (RH), and temperature, to manage the conditions within the solid bed. This can be done in two ways: either controlling the humidity of the air while keeping its temperature constant, or controlling the temperature of the air while keeping its humidity constant [14]. However, in most fungal SSF studies, the variation of the moisture solid substrate was manually studied, conditioning its humidity at the beginning of fermentation, and then keeping a constant relative humidity airflow [15,16,17,18,19].
The air conditioning configurations can vary from simple systems where air enters through a blower, to a system with an air filter, followed by a humidification tank with porous plate (humidifier); to alternatives where humidification columns are used, along with hot and cold water tanks with solenoid valves that allow mixing these water streams to condition the air temperature. The choice between one configuration or another will depend on criteria such as economic performance, capital cost of the devices, and operational costs (blowing the air, heating or cooling the air, producing steam, and heating water) [14]. Based on this, it would be feasible and simple to use air with a variable relative humidity percentage throughout the SSF.
In this study, we proposed a simple and innovative method aimed at maximizing LA production derived from solid state fermentation of grape stalk (a byproduct of the wine industry in San Juan, Argentina), employing Rhizopus oryzae NCIM 1299 (from Centro de Referencia de Micología, Facultad de Ciencias Bioquímicas y Farmacéuticas, Universidad Nacional de Rosario, Rosario, Argentina).

2. Materials and Methods

The general procedure for obtaining a variable relative humidity profile that maximizes LA production is described in Figure 1:

2.1. Experimental Data of SSF

As shown in Figure 1, the workflow diagram of the study was based on experimental data from the growth kinetics of R. oryzae NCIM 1299 1299 on grape stalk. Growth experiments were conducted in Petri dishes by membrane filter culture system, using grape stalk (as solid substrate) and agar agar (as gelling agent), methodology detailed in [20]. This system was used because it mimics the conditions in SSF and it is a simple manner to collect the biomass off the filter without penetrating through the structure of the grape stalk. Samples were taken every 12 h, and the dry biomass of R. oryzae was quantified by gravimetry [16] and the concentration of LA by spectrophotometric technique [21].
It was chosen to work by manipulating the ambient relative humidity (RH) and not the moisture substrate, because RH is the manipulable parameter in a bioreactor through the injection of saturated air into the bioprocess, whereas moisture substrate can be conditioned at the beginning of the SSF and maintained at an optimal level using humidified air [22]. Therefore, it can be assumed that the solid substrate and the fungus are at the ambient temperature and relative humidity of the air in the incubation chamber due to the following considerations:
(a)
To avoid the effect of the moisture gradient that may occur in the substrate of SSF, agar was chosen as it is a strong gelling agent with a high water retention capacity (up to 20 times its own weight) [23]. Additionally, a sufficient layer of culture medium (Agar+GS) was placed to ensure that it does not influence mass transfer effects.
(b)
The nylon filter (0.2 µm porosity) placed between the culture medium and the fungus allows the fungus to grow under the existing ambient conditions above the nylon filter. However, at the same time, the fungus is in indirect contact with the culture medium, which contains retained water for the proper metabolic development of the fungus.
Three experiments were carried out in an incubator (SEMEDIC, L-291PH) with temperature and humidity control, using a fixed temperature of 35 °C following three constant relative humidity values: 50, 65, and 80 %RH. These conditions were chosen based on others fungal SSF works. Firstly, a study on the effect of humidity (45 to 85% w/w) on the production of LA produced by R. oryzae in pineapple residues was taken as a basis [18]. Also, in [19], the influence of wheat moisture on cellulase production by Aspergillus oryzae was studied using four moisture levels, 50, 60, 70, and 80 %, while maintaining the temperature constant at 35 °C. Another study utilized moisture levels of 30, 40, 50, and 60 %, but also varying the temperature by 20, 30, 40 and 50 °C, to evaluate the effect of humidity on enzyme production by Aspergillus niger [16].

2.2. Mathematical Modeling and Parametric Identification

Once the experimental data from the bioprocess were obtained, mathematical models were chosen to adequately represent the kinetic behavior of fungal biomass production and lactic acid production. Mathematical models were adjusted to these kinetic curves: on the one hand, the Logistic (see equation 1 from Figure 1) and First Order Plus Dead Time (FOPDT) model (see equation 2 from Figure 1) models were used to describe biomass generation, and on the other hand, the Luedeking and Piret with Delay Time model (LPwDT) model (see equation 3 from Figure 1) was applied to describe LA production [24,25].
In equations 1 to 3 of Figure 1, the kinetic parameters highlighted in yellow are those that need to be optimized to obtain the best value of the coefficient of determination R2 for each model: Xmax, μmax, tp, t0, Yp/x, and td. To achieve this objective, a hybrid algorithm [26] was applied, which combines a probabilistic method, Monte Carlo Method, that generates an initial population of parameters randomly through a random algorithm and selects the best ones. Then, this group of parameters is refined using an evolutionary optimization technique, Genetic Algorithm Method, which solves search and optimization problems based on the genetic process of living organisms.
The mathematical models for each kinetic growth and LA production were fitting with Matlab R2015a software.

2.3. Humidity Polynomial Relationship with the Kinetic Parameters

Once the values of the kinetic parameters that maximized the R2 value of each mathematical model were elucidated, they were related to the relative humidity using a second-degree polynomial relationship:
f R H = a 1 R H 2 + a 2 R H + a 3
where f is the kinetic parameter (μmax, Xmax, tp, t0, and Yp/x), a1, a2, and a3 are the adjustment parameters, and RH is the relative humidity. The Matlab R2015a curve fitting tool was used to obtain the graphs, by applying a grade 2 polynomic regression.
Mathematically, polynomials can be applied to different systems under study, with no limitation on application whether the substrate is liquid or solid. Our team has been working on polynomial fitting in other systems, such as the biocontrol of wine spoilage yeasts and the study of the variation of kinetic parameters obtained at different pH levels [27].
Regarding SSF, the use of polynomials was implemented to establish a relationship between the kinetic parameters of mathematical models and relative humidity, rather than to describe the kinetics of the fermentation process.

2.4. Optimal Control Problem Statement and Lactic Acid Maximization Using Dynamic Optimization

The statement of the optimal control problem (OCP) was established in Figure 1. The OCP consists of setting the objective function, in our case, maximizing the concentration of lactic acid at the end of the fermentation (120 h), by finding the optimal profile of relative humidity over time. To do this, clear initial conditions, equality constraints, and inequality constraints of the bioprocess were outlined (see Figure 1).
The set of kinetic parameters polynomials obtained previously, were the input data to obtain the variable relative humidity profile. This profile was obtained applying the Dynamic Optimization Technique, based on Fourier Series and Orthogonal Polynomials. The basis of this technique is to use the first terms of the Fourier series to obtain a polynomial with a minimal number of parameters to optimize. Then, a transformation is performed from the Fourier polynomial basis to an Orthonormal basis. This results in a smooth relative humidity (RH) profile with low frequency (from a mathematical perspective), providing a good representation of the system with a minimum number of parameters to optimize. The complete mathematical description of this technique is sufficiently detailed in [28].
Programming was carried out using Matlab R2015a software to obtain the variable relative humidity profile.

3. Results and Discussion

3.1. Experimental Data of SSF, Mathematical Modeling and Parametric Identification

The Figure 2 presents the averages with their error bar of the R. oryzae experimental results at the three % RH carried out:
It can be observed that there was not a significant difference in the growth kinetics carried out at 65 %RH and 80 %RH levels, but a clear difference was observed at 50 %RH. This confirms that R. oryzae NCIM 1299 preferred lower humidity levels for its proper development, indicating that SSF is a suitable bioprocess for lactic acid production with this type of microorganism. This is further confirmed by the values of the optimal kinetic parameters of the fitted models, as shown in Figure 2 and Table 1:
Regarding the adjustment of microbial growth models with the variation of RH, it is observed that the R2 values were similar for the Logistic model and FOPDT model, with a slight improvement in R2 when applying the FOPDT model. With these results, it is only reaffirming the convenience of using the FOPDT model in the modeling of bioprocesses, due to the simplicity and wide knowledge of this model in other branches of engineering, such as chemical or electronic processes, among others.
It is important to note that in the present study, no growth morphology variation was observed in R. oryzae NCIM 1299 was observed, as it always grew in a mycelial form. In contrast, in the previous study on the effect of temperature [25], there was a change in the morphology of the fungus, with pellet growth observed at 40 °C and 50 %RH. This could indicate that there is no direct effect of RH on fungal metabolism related to morphological changes, as is the case with temperature. Therefore, it can be said that RH would not be a parameter to manipulate when studying the improvement in LA productivity through the use of R. oryzae pellets.
Next, the Figure 3 presents the averages with their error bar of the LA experimental results at the three RH carried out:
It can be seen that SSF carried out at 50 %RH and 65 %RH did not show significant differences between them, while at 80 %RH, a considerable increase in LA production was observed. This could be due to the fact that, at an 80 %RH, the fungus exhibited the lowest amount of biomass produced (Xmax) compared to 50 %RH and 65 %RH (see Figure 2). This could be attributed to mycelium compaction due to the high humidity content. Therefore, as biomass production was restricted, the fungus dedicated itself to producing a greater quantity of the metabolite LA. This behavior was also observed in [17], where the effect of humidity on the production of antioxidant naphtho-gamma-pyrones and hydroxycinnamic acids by Aspergillus tubingensis in SSF was studied. Here, biomass production decreased with increasing humidity, while metabolite production increased.
In Table 2, the models and parameters adjusted at each %RH worked on are presented:
In all three conditions, there is an improvement in the R2 values when using the FOPDT model with LPwDT. The Yp/x values of both models clearly reflect the aforementioned suitability of working at higher %RH to achieve higher AL productions, as shown in Figure 7.12. It is interesting to note that at 80 %RH (see Table 2), there is a delay of td = 5 h, which reflects the difficult adaptation of the fungus to high humidities, but which it later compensates with high LA yields.

3.2. Humidity Polynomial Relationship with the Kinetic Parameters

On page 237 of [29], Theorem 5.1.4 is found, which states that if a system is subjected to presenting small variations in parameters, then the responses should not be very different from each other. In this sense, if the RH changes very little, it is expected that the results will be very similar to the original experience. This suggests that if the parameters change following a certain function, this function must be continuous with continuous derivatives. While the exact form of the function representing the parameter variation is unknown by us, we can know that it will have the aforementioned properties. Furthermore, it is possible to apply the Stone-Weierstrass Theorem (Theorem 5.6, page 21, from [30]). This theorem states that real continuous functions defined on a closed and bounded interval can be approximated as closely as desired by a polynomial. Additionally, real-coefficient polynomials are dense in the set of continuous functions over a closed interval.
Based on this, a second-degree polynomial was chosen since the considered RH interval is 30 % (from 50 to 80 %RH). In this interval, it is not expected that the parameters exhibit multiple local maximum and minimum. What is expected is that the parameters show a maximum, a minimum, or exhibit monotonic behavior, in which case the maxima or minima will be at the limits of the considered interval. For all these reasons, a second-degree polynomial was used to fit the kinetic parameters with temperature.
The need to use a higher order polynomial would be because we expect to obtain multiple maxima and minima. It can be seen that the P3 polynomial of Legendre polynomials, for example, has 3 roots in the considered interval; the P4 polynomial has 4 roots, and so on (Section 4.5, pages 226 to 230, from [31]). If we use more points to fit a higher order polynomial, it means that the parameter could present, for example, two maxima and one minimum in the case of a 4th-order approximation, which does not align with the assumptions of our work.
Therefore, Figure 4 shows the second-degree polynomials that related the variation of each parameter versus relative humidity:
As shown in Figure 4, a decrease in the value of Xmax can be observed with the increase in RH, which is consistent with what was reported in work [32], where they established that a higher water activity in the solid bed favors fungal sporulation, while a lower water activity favors mycelial growth. This could be due to an excess dissolution of the nutrients present in the SSF, which could affect the amount of biomass obtained. Additionally, as reported in [33], in the case of aerobic fungi, the increase in water content in the substrate hinders the stretching of the mycelium in the pores of the solid substrate, since the oxygen diffusion rate in water is only 1/200,000 compared to that in air, making the water film tension a limiting factor that affects mycelial extension. However, in [16] and [34], the value of Xmax increases with the increase in RH, although the humidity ranges studied were from 30 to 60 % and from 45 to 65 %, respectively, considerably lower than those studied in the present thesis, which ranged from 50 % to 80 % RH.
Regarding the FOPDT model kinetic parameters, it is observed that in relation to the parameter tp, the best value (3.22 h) was obtained at 60.37 %RH, with the RH value being very close to that obtained with the µmax in Logistic model. In addition, a decrease in the value of t0 is observed with the increase in %RH, reflecting a better adaptation of the microorganism with RH increases. Despite Xmax decreasing with increasing RH, contrary to the increase in t0, it can be said that these are parameters characterizing the behavior of the microorganism in different growth stages of the fungus, with t0 representing the adaptation phase of the fungus and Xmax representing the stationary phase. Therefore, these relationships may be valid.

3.3. Lactic acid Maximization Using Dynamic Optimization

Once all the steps mentioned in Figure 1 have been applied, it is now possible to determine whether the application of Dynamic Optimization technique achieves higher LA yields compared to those obtained in the experimental phase. The variable RH profile obtained and the LA maximized are shown in Figure 5:
It can be clearly observed in Figure 5(a) that applying a variable RH profile results in savings in terms of the amount of water required to humidify the SSF system. This can be estimated by graphically calculating the area under the curve for both treatments, with 50 %RH as the lower limit and 80 %RH as the upper limit, over the duration of the 120 h bioprocess. Thus, a 33 % decrease in the amount of water required is obtained when applying the variable HR profile compared to the constant profile (80 %RH). Therefore, the process with a variable RH profile would be more environmentally friendly compared to the constant RH process.
It is important to note that most of the fungal SSF studies found so far have focused on the effect of varying the initial moisture content of the solid substrate while keeping the humidified air flow static throughout the bioprocess [15,16,17,18,19]. Furthermore, one study was proposed a humidity control strategies based in capillary-water supply to control temperature and RH in SSF tray bioreactor [14]. No SSF studies with RH control strategies applying a variable RH profile were found. In this regard, the present study is innovative as it proposes an alternative approach with a variable RH profile, a biotechnological aspect that has not been extensively explored so far.
Figure 5(b) shows the LA production obtained after applying the dynamic optimization technique compared to the LA production obtained at 80 %RH. It can be observed that the optimized LA production accelerates from the beginning of the fermentation, with the parameter td = 0. This result indicates that the variable RH profile had a direct influence on the parameter td, evidencing the disappearance of a delay time between fungal biomass and LA production. Then, there is a clear presence of an increasing ramp of LA production from 50 h, reaching 120 h with a 15.30% increase in yield compared to the LA production curve at 80 %RH.
As mentioned earlier, manipulating the RH parameter is relatively easy, as the procedure for injecting humid air is a simple technological process to implement [12]. Additionally, the humidified air injection system allows for cooling of the system and provides oxygen in the case of aerobic SSF [14]. Furthermore, implementing smooth and continuous variations of bioprocess parameters is more suitable than applying step changes, as they can affect the final yield of the metabolite under study.

4. Conclusions

In this work, we presented a dynamic optimization strategy based on Fourier Series and Orthogonal Polynomials, which allowed us to obtain a variable RH profile (smooth, continuous, and differentiable) that maximized LA production. Under experimental conditions, the highest LA production was 0.181 gLA/gGS at 80% RH and 35°C, while applying the variable RH profile resulted in 0.2087 gLA/gGS at the end of the bioprocess, representing a 15.30 % increase. This optimized result could not have been achieved without a methodologically appropriate approach in the experimental stage, as it allowed us to fit mathematical models to the data obtained. The versatility of these models lies in their ability to accurately represent reality, with intuitive and easy to calculate parameters. The use of the hybrid parametric identification technique reduced the convergence time of the Matlab R2015 software compared to traditional methods. The application of second-order polynomials to relate the variation of kinetic parameters to relative humidity was appropriate and confirmed the versatility of polynomials in describing the variability of kinetic parameters in a wide range of biological systems. The strategy proposed in this work is considered to have great potential for application in other bioprocesses, as they are generally nonlinear, highly variable, and complex systems, as is the case of SSF. Based on the results obtained, our group intends to investigate in future work the behavior of fungal bioprocesses for LA production by applying a variable profile of both relative humidity and temperature. The objective will be to correlate the system's response to the time variation of both parameters.

Author Contributions

Conceptualization, M.C.G., S.E.N., and G.S.; methodology, M.C.G. and L.R.; software, G.S. and B.K.; formal analysis, M.C.G. and S.E.N.; investigation, M.C.G.; writing—original draft preparation, M.C.G.; writing—review and editing, M.C.G., S.E.N. and G.S.; supervision, S.E.N. and G.S. All authors have read and agreed to the published version of the manuscript.

Funding

This article was financially supported by Universidad Católica de Cuyo (UCCuyo; CAM-5-2015; Res. No. 0289-CS-2017) and Secretaría de Ciencia, Tecnología e Innovación (SECITI, SECITI-UCCuyo-2017; Res. No. 0656-CS-2019).

Institutional Review Board Statement

This article does not contain studies with human participants or animals performed by any of the authors.

Informed Consent Statement

Informed consent was obtained from all individual participants included in the study.

Data Availability Statement

All the data are provided in this manuscript.

Acknowledgments

The authors are grateful to the staff of the Laboratorio de Control de Calidad Alberto Graffigna of the Universidad Católica de Cuyo for their collaboration and predisposition; they allowed us access to their facilities for the development of different laboratory techniques. The companies SolFrut Alimentos and the winery Tierra del Huarpe S.A. contributed by facilitating the use of some equipment and donated raw material for this research. Likewise, the authors thank the Consejo Nacional de Investigaciones Científicas y Técnicas de Argentina (CONICET), the Universidad Católica de Cuyo, the Universidad Nacional de San Juan, and the Secretaría de Ciencia, Tecnología e Innovación (SECITI, San Juan) for the financial support provided to the doctoral fellow María Carla Groff.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Alves De Oliveira, R.; Komesu, A.; Vaz Rossell, C.E.; Filho, R.M. Challenges and Opportunities in Lactic Acid Bioprocess Design—From Economic to Production Aspects. Biochem. Eng. J. 2018, 133, 219–239. [Google Scholar] [CrossRef]
  2. Obi, F.; Ugwuishiwu, B.; Nwakaire, J. Agricultural Waste Concept, Generation, Utilization and Management. Niger. J. Technol. 2016, 35, 957. [Google Scholar] [CrossRef]
  3. Papaioannou, E.H.; Mazzei, R.; Bazzarelli, F.; Piacentini, E.; Giannakopoulos, V.; Roberts, M.R.; Giorno, L. Agri-Food Industry Waste as Resource of Chemicals: The Role of Membrane Technology in Their Sustainable Recycling. Sustain. 2022, 14, 1–21. [Google Scholar] [CrossRef]
  4. MordorIntelligence Análisis de Participación y Tamaño Del Mercado de Productos Biológicos Tendencias de Crecimiento y Pronósticos (2024-2029) Available online: https://www.mordorintelligence.com/es/industry-reports/biologics-market.
  5. Arthur, D. Little Why Bio-Based Materials Market Finally Poised Growth? Available online: https://www.adlittle.com/en/insights/prism/why-bio-based-materials-market-finally-poised-growth.
  6. Baeza, J.A. Principles of Bioprocess Control. In Current Developments in Biotechnology and Bioengineering: Bioprocesses, Bioreactors and Controls; Elsevier B.V., 2017; pp. 527–561 ISBN 9780444636744.
  7. Ge, X.; Vasco-Correa, J.; Li, Y. Solid-State Fermentation Bioreactors and Fundamentals. In Current Developments in Biotechnology and Bioengineering: Bioprocesses, Bioreactors and Controls; 2017; pp. 381–402 ISBN 9780444636744.
  8. Pandey, A. Solid-State Fermentation. Biochem. Eng. J. 2003, 13, 81–84. [Google Scholar] [CrossRef]
  9. Utilizing, P.; Grain, C.; Manandhar, A.; Shah, A. Techno-Economic Analysis of Bio-Based Lactic Acid. 2020.
  10. Rahim, N.A.; Luthfi, A.A.I.; Abdul, P.M.; Jahim, J.M.; Bukhari, N.A. Towards Sustainable Production of Bio-Based Lactic Acid via a Bio-Based Technical Route: Recent Developments and the Use of Palm Kernel Cakes in the Bioconversion. BioResources 2022, 17, 3781–3809. [Google Scholar] [CrossRef]
  11. Webb, C.; Manan, M.A. Design Aspects of Solid State Fermentation as Applied to Microbial Bioprocessing. J. Appl. Biotechnol. Bioeng. 2017, 4, 511–532. [Google Scholar] [CrossRef]
  12. Mitchell, D.A.; Berovič, M.; Krieger, N. Solid-State Fermentation Bioreactors; Springer: Berlin, Heidelberg, 2006; ISBN 9783540312857. [Google Scholar]
  13. He, Q.; Peng, H.; Sheng, M.; Hu, S.; Qiu, J.; Gu, J. Humidity Control Strategies for Solid-State Fermentation: Capillary Water Supply by Water-Retention Materials and Negative-Pressure Auto-Controlled Irrigation. Front. Bioeng. Biotechnol. 2019, 7, 1–13. [Google Scholar] [CrossRef]
  14. Sentís-Moré, P.; Romero-Fabregat, M.P.; Rodríguez-Marca, C.; Guerra-Sánchez, A.J.; Ortega-Olivé, N. Design Optimization of a Tray Bioreactor for Solid-State Fermentation: Study of Process Parameters through Protein Modification of By-Products. Fermentation 2023, 9. [Google Scholar] [CrossRef]
  15. Wang, H.; Sun, C.; Yang, S.; Ruan, Y.; Lyu, L.; Guo, X.; Wu, X.; Chen, Y. Exploring the Impact of Initial Moisture Content on Microbial Community and Flavor Generation in Xiaoqu Baijiu Fermentation. Food Chem. X 2023, 20, 100981. [Google Scholar] [CrossRef]
  16. Saithi, S.; Borg, J.; Nopharatana, M.; Tongta, A. Mathematical Modeling of Biomass and Enzyme Production Kinetics by Aspergillus Niger in Solid-State Fermentation at Various Temperatures and Moisture Contents. J. Microb. Biochem. Technol. 2016, 08, 123–130. [Google Scholar] [CrossRef]
  17. Carboué, Q.; Rébufa, C.; Hamrouni, R.; Roussos, S.; Bombarda, I. Statistical Approach to Evaluate Effect of Temperature and Moisture Content on the Production of Antioxidant Naphtho-Gamma-Pyrones and Hydroxycinnamic Acids by Aspergillus Tubingensis in Solid-State Fermentation. Bioprocess Biosyst. Eng. 2020, 43, 2283–2294. [Google Scholar] [CrossRef]
  18. Zain, N.A.M.; Aziman, S.N.; Suhaimi, M.S.; Idris, A. Optimization of L(+) Lactic Acid Production from Solid Pineapple Waste (SPW) by Rhizopus Oryzae NRRL 395. J. Polym. Environ. 2021, 29, 230–249. [Google Scholar] [CrossRef]
  19. Pirota, R.D.P.B.; Tonelotto, M.; Delabona, P.S.; Fonseca, R.F.; Paixão, D.A.A.; Baleeiro, F.C.F.; Bertucci Neto, V.; Farinas, C.S. Bioprocess Developments for Cellulase Production by Aspergillus Oryzae Cultivated under Solid-State Fermentation. Brazilian J. Chem. Eng. 2016, 33, 21–31. [Google Scholar] [CrossRef]
  20. Groff, M.C.; Scaglia, G.; Gaido, M.; Kassuha, D.; Ortiz, O.A.; Noriega, S.E. Kinetic Modeling of Fungal Biomass Growth and Lactic Acid Production in Rhizopus Oryzae Fermentation by Using Grape Stalk as a Solid Substrate. Biocatal. Agric. Biotechnol. 2022, 39. [Google Scholar] [CrossRef]
  21. Borshchevskaya, L.N.; Gordeeva, T.L.; Kalinina, A.N.; Sineokii, S.P. Spectrophotometric Determination of Lactic Acid. J. Anal. Chem. 2016, 71, 755–758. [Google Scholar] [CrossRef]
  22. Webb, C. Design Aspects of Solid State Fermentation as Applied to Microbial Bioprocessing. J. Appl. Biotechnol. Bioeng. 2017, 4, 511–532. [Google Scholar] [CrossRef]
  23. Bermudez, A. AGAR-AGAR, La Versatilidad de Un Ingrediente En Expansión Available online: https://granotec.com.ar/agar-agar-la-versatilidad-de-un-ingrediente-en-expansion/#:~:text=La funcionalidad del agar radica,resistentes que la gelatina común.
  24. Groff, M.C.; Scaglia, G.; Ortiz, O.A.; Noriega, S.E. Modification of the Luedeking and Piret Model with a Delay Time Parameter for Biotechnological Lactic Acid Production. Biotechnol. Lett. 2022, 0. [Google Scholar] [CrossRef]
  25. Groff, M.C.; Noriega, S.E.; Gil, R.M.; Pantano, N.; Scaglia, G. Dynamic Optimization of Lactic Acid Production from Grape Stalk Solid-State Fermentation with Rhizopus Oryzae Applying a Variable Temperature Profile. Fermentation 2024, 10, 101. [Google Scholar] [CrossRef]
  26. Fernández, C.; Pantano, N.; Godoy, S.; Serrano, E.; Scaglia, G. Optimización de Parámetros Utilizando Los Métodos de Monte Carlo y Algoritmos Evolutivos. Aplicación a Un Controlador de Seguimiento de Trayectoria En Sistemas No Lineales. Rev. Iberoam. Automática e Informática Ind. 2018, 00, 1–4. [Google Scholar] [CrossRef]
  27. Kuchen, B.; Garay, S.A.; Gil, R.M.; Vazquez, F.; Scaglia, G.J.E. Optimization of Batch Reactors : Application to the Biocontrol of Spoilage Yeasts in Wines. IEEE Lat. Am. Trans. 2022; 100. [Google Scholar]
  28. Pantano, M.N.; Fernández, M.C.; Ortiz, O.A.; Scaglia, G.J.E.; Vega, J.R. A Fourier-Based Control Vector Parameterization for the Optimization of Nonlinear Dynamic Processes with a Finite Terminal Time. Comput. Chem. Eng. 2020, 134, 106721. [Google Scholar] [CrossRef]
  29. Agarwal, R.P. Difference Equations and Inequalities: Theory, Methods, and Applications; CRC Press. 2000. [Google Scholar]
  30. John, B. Conway A Course in Functional Analysis; second; Springer: New York, NY, USA, 2007; volume 5, ISBN 9788578110796. [Google Scholar]
  31. Oliver, P.J.; Shakiban, C. Applied Linear Algebra; Springer International Publishing AG, 2018; ISBN 9783319910406.
  32. Manpreet, S.; Sawraj, S.; Sachin, D.; Pankaj, S.; Banerjee, U.C. Influence of Process Parameters on the Production of Metabolites in Solid-State Fermentation. Malalaysian Jounal Microbiol. 2005, 1, 1–9. [Google Scholar] [CrossRef]
  33. Chen, H. Modern Solid State Fermentation Theory and Practice; Springer.: Netherlands, 2013; ISBN 9789400760424. [Google Scholar]
  34. Hamidi-Esfahani, Z.; Shojaosadati, S.A.; Rinzema, A. Modelling of Simultaneous Effect of Moisture and Temperature on A. Niger Growth in Solid-State Fermentation. Biochem. Eng. J. 2004, 21, 265–272. [Google Scholar] [CrossRef]
Preprints 101953 g001
Figure 1. Procedure applied to obtain the variable relative humidity profile of the SSF to maximize LA production. Where: dX/dt: R. oryzae growth rate [g dry biomass/g dry grape stalk·h, g DB/g GS·h], X: fungal biomass concentration obtained for a specific amount of time [g DB/g GS]; μmax: maximum specific growth rate [1/h]; Xmax: maximum biomass concentration [g DB/g GS]; X0: R. oryzae inoculum [g DB/g GS], t0: the time range in which there is no fungal biomass growth (latency phase) [h]; tp: the parameter of the bioprocess that provides information on the speed of growth up to Xmax [h]; dP/dt: the LA production rate [g LA/g GS·h]; Yp/x: the LA yield [g LA/g DB]; P0: the initial LA concentration [g LA/g GS]; td: the time difference between when LA production and biomass generation starts [h] and t: time [h].
Figure 1. Procedure applied to obtain the variable relative humidity profile of the SSF to maximize LA production. Where: dX/dt: R. oryzae growth rate [g dry biomass/g dry grape stalk·h, g DB/g GS·h], X: fungal biomass concentration obtained for a specific amount of time [g DB/g GS]; μmax: maximum specific growth rate [1/h]; Xmax: maximum biomass concentration [g DB/g GS]; X0: R. oryzae inoculum [g DB/g GS], t0: the time range in which there is no fungal biomass growth (latency phase) [h]; tp: the parameter of the bioprocess that provides information on the speed of growth up to Xmax [h]; dP/dt: the LA production rate [g LA/g GS·h]; Yp/x: the LA yield [g LA/g DB]; P0: the initial LA concentration [g LA/g GS]; td: the time difference between when LA production and biomass generation starts [h] and t: time [h].
Preprints 101953 g001
Preprints 101953 g002
Figure 2. Mathematical models adjusted to R. oryzae growth kinetic curves at 50, 65 and 80 %RH.
Figure 2. Mathematical models adjusted to R. oryzae growth kinetic curves at 50, 65 and 80 %RH.
Preprints 101953 g002
Preprints 101953 g003
Figure 3. Mathematical models adjusted to lactic acid production kinetic curves at 50, 65 and 80 %RH.
Figure 3. Mathematical models adjusted to lactic acid production kinetic curves at 50, 65 and 80 %RH.
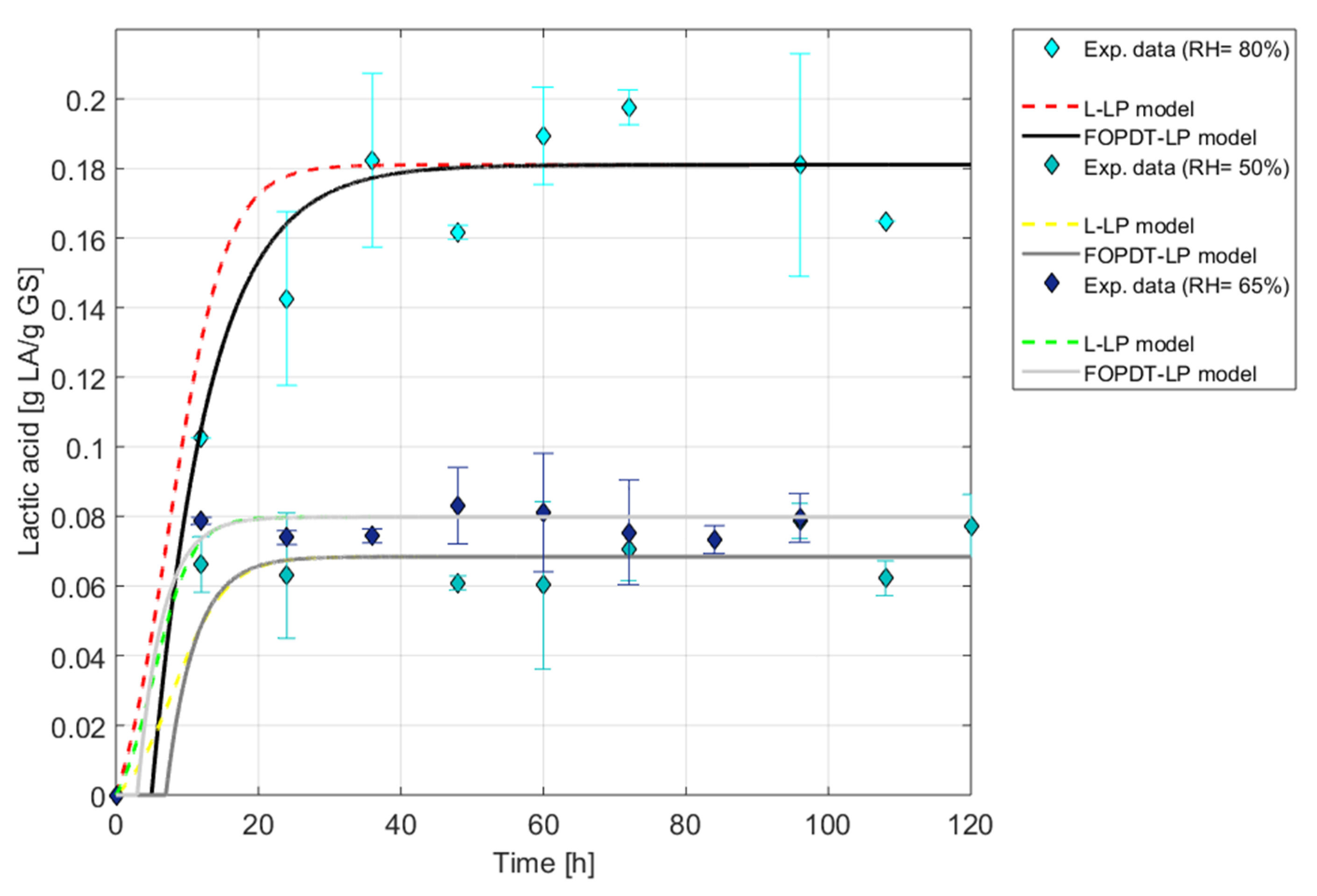
Preprints 101953 g003
Preprints 101953 g004aPreprints 101953 g004b
Figure 4. Polynomial relation between the kinetic parameters and relative humidity.
Figure 4. Polynomial relation between the kinetic parameters and relative humidity.
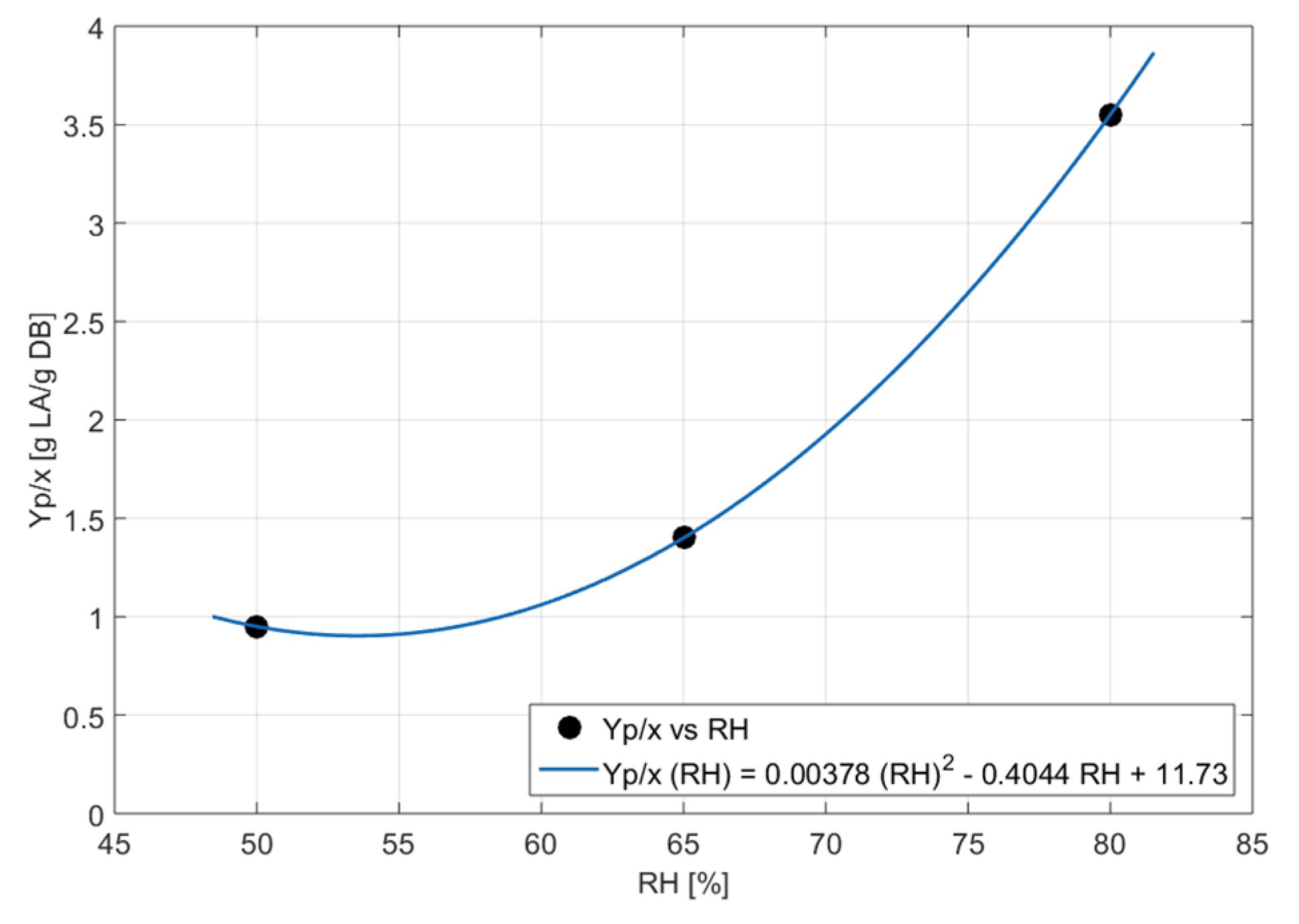
Preprints 101953 g004aPreprints 101953 g004b
Preprints 101953 g005
Figure 5. Effect of RH profile application on LA production. (a) RH vs time (b) LA obtained at 80 % RH and by applying a variable RH profile.
Figure 5. Effect of RH profile application on LA production. (a) RH vs time (b) LA obtained at 80 % RH and by applying a variable RH profile.
Preprints 101953 g005
Table 1. Fungal growth kinetic parameters of mathematical models obtained at different constant relative humidity.
Table 1. Fungal growth kinetic parameters of mathematical models obtained at different constant relative humidity.
Experimental Conditions R. oryzae Growth
Logistic Model FOPDT Model
T RH X0 Xmax µmax R2 tp t0 R2
35 50 0.008 ± 0.002 0.080 ± 0.002 0.270 ± 0.008 82.77 4.50 ± 0.12 7.00 ± 0.23 83.55
65 0.065 ± 0.002 0.370 ± 0.011 91.68 3.50 ± 0.11 3.00 ± 0.08 91.67
80 0.059 ± 0.002 0.250 ± 0.008 98.13 8.00 ± 0.25 2.00 ± 0.05 98.31
Table 2. Lactic acid production kinetic parameters of mathematical models obtained at different constant relative humidity.
Table 2. Lactic acid production kinetic parameters of mathematical models obtained at different constant relative humidity.
Experimental Conditions Lactic Acid Production
Luedeking and Piret with Delay Time model
Logistic Model FOPDT Model
T RH X0 Yp/x R2 Yp/x td R2
35 50 0.008 ± 0.002 0.95 ± 0.027 82.45 0.95 ± 0.027 0 81.09
65 1.40 ± 0.040 83.76 1.40 ± 0.040 0 96.89
80 3.55 ± 0.370 84.33 3.55 ± 0.370 5 ± 0.16 94.52
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Determination of Variable Humidity Profile for Lactic Acid Maximization in Fungal Solid-State Fermentation

María Carla Groff

et al.

,

2024

Development of a Novel Approach for Controlling and Predicting Residual Sugars in Wines

Ronit Yaa’ri

et al.

,

2024

Nucleation Triggering of Highly Undercooled Xylitol Using an Air Lift Reactor for Seasonal Thermal Energy Storage

Marie Duquesne

et al.

,

2019

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated