Preprint

Article

Pulsed Propulsion of Unmanned Aerial Vehicles by Centrifugal Force Modulation - First-Order Theory and Practicability

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Wolfgang Holzapfel Dr.^*

This version is not peer-reviewed

Submitted:

12 March 2024

Posted:

28 March 2024

You are already at the latest version

Alerts

Abstract

A novel technique suitable for propulsion of small unmanned aerial vehicles (UAV) is discussed in this paper. This approach utilizes the rotational energy of airborne gyro rotors and converts it into translational propulsion for the vehicle. The energy conversion is achieved by generating precisely directed centrifugal force pulses through short-duration rotor unbalances. The accurate control of the timing and magnitude of these unbalances is crucial for successful propulsion generation. Our first-order theory of controlled unbalance propulsion (CUP) predicts the potential for achieving high translational accelerations and vehicle velocities up to orbital levels. Power saving levitation of UAVs can be attained. In this paper, we provide traceable evidence that pulsed centrifugal propulsion is based on well-established laws of physics and can be realized using state-of-the-art technologies.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

The idea of generating propulsion through rotating unbalance is by no means new. There is nothing told about this inertial technology in actual publications [1,2,3], which are reviewing the state of the art in different propulsion technologies for unmanned aerial vehicles (UAV). Contrary, in the patent literature, there are already various approaches for so-called centrifugal force drives that propose the use of rotors with asymmetric mass distribution, e.g., [4,5,6,7], However, these have so far not led to any functional realizations. The proposed methods are controversial in the scientific community, not least because they seem to violate the physical law of conservation of momentum and because the rotating centrifugal force, as a pseudo force, could not cause a lasting translation of the rotor's center of mass. Currently, there are apparently no contributions or discussions on this topic in reputable scientific journals. On the other hand, it is well known that the rotational energy of masses can be successfully utilized for energy storage purposes, as seen in the online article [8] on Wikipedia, as well as the online contribution [9] by the Max Planck Institute for Plasma Physics, 2021. An up-to-date overview of the design and optimization of flywheel energy storage systems in automotive engineering is available in reference [10].

This paper presents the first demonstration of quantitative designing a centrifugal force drive that utilizes (1st) flywheel energy storage and (2nd) transfers that energy into vehicle movement. It is based completely on known laws of physics and therefore such drive will work in principle. It is shown that a basic prerequisite for a functional drive is the precise spatial rectification of the vector of the resulting centrifugal force. This, in turn, can be achieved by a rapid temporal impulse modulation of the unbalance-induced force amplitude. Furthermore, we state here, that this novel kind of drive could be technically effective for small UAVs.

2. First Order Theory of Propulsion Generation by Means of Rotation Energy

Assume a stiff rotor disc (radius R, thickness D<R, homogenic material distribution, total mass M) equipped with fixed unbalance mass m_u at its periphery (Figure 1). The disc rotation axis A should be perpendicularly centered in a planar system with orthogonal axes (x; y), fixed in an inertial reference frame. We apply in the following discussion the equivalent circuit mass point diagram of Figure 1 (right).

Due to disc rotation the generated centrifugal force vector written in polar coordinates is

\begin{array}{l} {\vec{F}}_{u} = \vec{R} m_{u} ω^{2} \\ \vec{R} = R e^{i (ω t + φ_{0})} \end{array}

(1)

with magnitudes

\vec{R}

radius vector (i = imaginary unit) pointing from axis A to unbalance mass m_u

φ₀ rotor fixed azimuth of unbalance mass point m_u

R radius of rotor disc

ω = 2πf (angular) revolution frequency

T = 1/f cycle time of rotor disc

Eq.1 says centrifugal force vector

{\vec{F}}_{u}

is always pointing in direction of instantaneous

\vec{R}

. Its magnitude F_u increases proportional with m_u and proportional with rotor radius R, furthermore F_u is increasing quadratic with applied rotor rotation frequency f.

It is useful to introduce unbalance vector

\vec{U}

that is vector

{\vec{F}}_{u}

divided by square of angular rotation frequency ω:

\vec{U} = U_{0} e^{i (ω t + φ_{0})} = m_{u} R e^{i (ω t + φ_{0})}

(2)

Note, unbalance magnitude U₀ = m_u R is independent of ω.

Due to peripheric unbalance mass m_u there is small displacement r of disc gravity center M arises, away from rotor rotation axis A. Note, this displacement is caused due to static balancing of the rigged disc. Additionally, elasticity and strain of real rotor materials may contribute to real displacement, but we will not take this effect into account here.

In case of very small unbalance mass m_u (i.e. M = M₀ + m_u , m_u << M₀ ≅ M) the following vector equation results:

M \vec{r} = m_{u} \vec{R}

(3)

respectively, for the magnitudes

M r = m_{u} R .

According to Eq. 3 the displacement r points always towards peripheric unbalance mass m_u. Thus, rotation axis A, disc mass M and unbalance mass point m_u are located on the same radius vector R (azimuth φ₀). Considering this we draw the conclusion: Vectorial displacement r of gravity center M can be controlled in principle via choosing magnitude and azimuth of the peripheric unbalance mass m_u !

Now the question arises: Is this mass displacement effect insignificant small or can it be used to the best advantage in propulsion technology?

To give the answer in Figure 2 the centrifugal force F_u is represented in in two orthogonal components:

F_ux = F_u cosφ_x (effective centrifugal force component, see below)

(4)

F_uy = F_u sinφ_x (noneffective centrifugal force component, see below)

(5)

φ_x = ωt ± mod2π instantaneous phase angle

t = 0: φ_x = 0
t = T: φ_x = 2π

Both components describe strictly harmonic forces having zero averages over each rotation period, i.e.

F_{x} = \frac{1}{2 π} \int_{0}^{2 π} F_{u x} d φ = 0

F_{y} = \frac{1}{2 π} \int_{0}^{2 π} F_{u y} d φ = 0

F_u instantaneous centrifugal vector symmetric to thrust direction x

F_x effective x-component of F_u

F_y noneffective-component of F_u

φ instantaneous rotation angle of F_u against x

Our approach to solve the problem how to get a non-zero resulting translatoric propulsion of the rotating disc: (partial) rectification of centrifugal force must be realized. For explaining need of force rectifikation let us assume here that wanted propulsion should appear in x-direction. Consequently, we habe to modulate unbalance during each rotation in following way (Figure 3): In an azimutal angle region 2α_x highly synnetric to the x-axis, i.e. the wanted propulsion direction, we generate non zero unbalance. Otherwise, outside of this region i.e. in the remaining region 2π -2α_x this unbalance is always compensated. Thus, within time period τ, which is only small fraction of cycle time T

τ/T = 2α_x / 2π

we have to switch on and off the rotor unbalance. If we succeed in managing this ultrafast modulation due to rotation we get a train of force impulses, each pulse of duration τ and separated by cycle time T from each other. This impulse train will result in significant change of the translational state of rotor mass M: According to Newton force F acting on mass point M equals the first derivate of its translational impulse P = Mv (v = translational velocity), thus

dP/dt = F(t)

(6)

ΔP = MΔv = F(t)Δt

The resulting impulse change during each rotation follows from

P = \int_{- τ / 2}^{τ / 2} F (t) d t = 2 \int_{0}^{τ / 2} F (t) d t

We get effective impulse component (x-component} of centrifugal force:

F(t) = F_ux (t) = F_u cos ωt

Δ P_{x} = \int_{0}^{T} F_{u} \cos ω t d t = \int_{- τ / 2}^{τ / 2} F_{u} \cos ω t d t

Δ P_{x} = \int_{0}^{τ / 2} F_{u} \cos ω t d t = 2 (F_{u} / ω) \sin ω τ / 2

(7)

Otherwise, due to the (ineffective) y-component of centrifugal force, zero average of impulse change is confirmed:

F_uy = F_u sinφ_x

Δ P_{y} = \int_{- τ / 2}^{τ / 2} F_{u y} d φ = 0

(8)

Let us assume for the angle of unbalance activity (Figure 3)

α_x ≤ π/2, sinα_x ≤ 1

we can rewrite (1.7) to get the non-zero force magnitude in x-direction

F_x = 4πm_uRf² sinα_x = m_uRω² sinα_x/_π resp. F_x = (4/π) Rω²m_u sinα_x

(9)

Based on Eq..7 - 9 above we conclude in summary:

Magnitude of propulsion force depends linearly on rotor radius R and on unbalance mass m_u and increases with square of rotational frequency f. For fixed values of unbalance mass m_u, rotor radius R and rotation frequency f propulsion force F_x will become its maximum if the unbalance is present in an angle range of 2α_x = 180°. Furthermore: Due to our intermitted operation of rotor unbalance only the wanted outward force component F_x (propulsion force) occurs in rotation plane. Propulsion force F_x , is orthogonal to rotation axis A and points exactly in wanted direction x, which is in symmetrical position within unbalance activity angle 2 α_x. On the other hand orthogonal force component F_y is extinguished over each rotation period. If there is no other restriction the unchained rotor will move exactly in direction x of the only acting force F_x. Its start point is x = 0 at time t = 0.

Here follows our description of takeoff scenario:

The UAV containing the well-balanced rotor on board is initially fixed in a constraining device at start position. After electrical loading the rotor spins with high rotation frequency. Translational energy of the fixed rotor is zero at the beginning of start phase because all kinetic energy is stored rotation energy. If we now would generate a permanent unbalance mass on the spinning rotor it will produce only rotating centrifugal force and unwanted vibrations of the cell and constraining device. But by controlled on/off-unbalance activation always in the same selected angle range during each revolution a sequence of force pulses in the wanted direction is generated due to permanent rotation which can be used now to produce directed propulsion of the vehicle cell. Thus, after opening the constraining device, the directed force pulse sequence will produce translational acceleration and causes movement of the UAV away from its start position.

3. Conversion of Rotational Energy into Translational Vehicle Energy

Pulsed propulsion by centrifugal force modulation can be applied in two modes of rotor energy management:

(1) The rotor could be used with an integrated onboard drive, able to deliver high and sustained electrical power output during the complete mission. Low weight and compact design of such combined power/propulsion system well suited onboard of a small UAV must be achieved here, which is not even an easy engineering task.

(2) Alternatively, the rotor will be brought to operating speed before takeoff through temporary mechanical coupling with a powerful external electric motor. The advantage of this pure inertial solution is much lower weight and more simplicity of the onboard propulsion system. But here the question arises, is there enough energy onboard of such UAV and how much is its flight performance and maneuverability limited?

We will focus here on management of this second energy mode because it seems better suited for small UAVs, at least in present state of technology. Furthermore, if successful combination of (1) and (2) would be feasible in future, our focus will deliver advanced performance.

When discussing the conversion of rotational energy (E_rot) into translational energy (E_trans) in the context of a UAV, it is important to consider the conservation of total kinetic energy (E₀) onboard the vehicle. According to the energy theorem, the total kinetic energy must remain constant. Therefore, we can express this conservation using the equation:

E₀ = E_rot + E_trans = const.

(10)

At the beginning of the takeoff scenario, when the UAV is at the starting point (x = 0), the maximum rotational energy is available. This can be represented as:

m a x E_{r o t} = \frac{1}{2} {θ ω_{0}}^{2} = E_{0}

(11)

with moment of disc inertia

θ = \frac{1}{2} {M R}^{2}

and maximum of rotation frequency:

ω₀ = 2πf₀

According (11), storable rotation energy increases proportional with rotor mass M and with square of disk radius R and square of rotation frequency f₀. Thus, for given size and material of the rotor disk a doubling of its rotation frequency f₀ will result in quadruple of mechanically stored airborne energy. Our conclusion: The store parameter f₀ is of high importance in flight performance evaluation. As per equation (11), the amount of storable rotational energy increases proportionally with the rotor mass (M), the square of the disk radius (R²), and the square of the rotation frequency f_{0 .}Therefore, if the rotation frequency f₀ is doubled while keeping the size and material of the rotor disk constant, the mechanically stored airborne energy will quadruple. This highlights the significance of the rotation frequency (f₀) as a parameter in evaluating flight performance (refer to chapter 4 for more details).

On the other hand, assuming ideal conditions in energy conversion i.e., friction free disc rotation and vehicle translation) and zero gravity space, the potential maximum of translational energy appearing at end of energy conversion is given by

m a x E_{t r a n s} = E_{0} = \frac{1}{2} {M' v}_{m a x}^{2} = M R^{2} {π^2 f}_{0}^{2}

(12)

This assumption is equivalent with 100 % efficiency in the conversion of the rotational energy to translational propulsion. It is also important to note that M' is larger than M, as M' represents the total mass of the UAV while M only represents the smaller mass of the rotor disc. The vehicle construction factor C, which is the ratio of M´ to M, can be assumed to be between 1 and 2 in realistic scenarios.

Thus, maximum translational velocity follows:

v_{m a x}^{2} = (\frac{1}{2}) R^{2} {ω o}^{2} M / M'

v_{m a x} = \frac{1}{\sqrt{2}} R ω o {(M / M')}^{1 / 2}

(13)

Maximum velocity v_max depends on radius R, angular velocity ω₀ and construction factor C = M´/M however, v_max is independent from unbalance mass m_u.

We are looking now on intermediate states of energy transformation: Energy theorem postulates that each increase of translational energy asks for equal decrease of rotational energy, i.e.

−dErot = dEtrans

(14)

E_rot = (1/4) M R² ω²

(15)

dE_rot = (1/4) MR²2ωdω = (1/2) MR²ωdω

(16)

E_trans = (1/2) M’ v2

(17)

(−1/2) MR²ω(dω/dt) = M' v (dv/dt)

(18)

(−1/2C) R²ω (dω/dt) = v a

(19)

Equation (19) teams our rotational magnitudes with the translational ones of interests, i.e. vehicle velocity v and its translational acceleration a.

Third axiom of Newton (actio = reactio) tells us about acceleration a of mass: Centrifugal force F = m_u R ω² caused by unbalance and inertial force F = M' a = M' d²x /dt² acting on vehicle mass M´ must be in equilibrium, i.e

M' a = m_u R ω²

(20)

Thus, we get the acceleration (a = dx²/dt² = dv/dt) of vehicle mass M':

a = (m_u /M') Rω²

(21)

From (19) follows time dependent change of rotation frequency:

dω/dt = −2 C v a /R²ω = −2(m_u /M R) vω

dω/ω = −2(m_u /M R) vdt

(22)

After integration we have:

\ln ω - \ln ω_{0} = - 2 (m_{u} / M R) \int_{0}^{x} v d t

(23)

ln ω/ω₀ = ln f/f0 = −2(m_u /M R) x

(24)

We get instantaneous rotation frequency in dependence of x = x(t), which is the trajectory length depending on trust duration time t:

ω = ω₀ exp {(-2m_u/M R) x}, resp. ω² = ω²₀ exp {(-4mu/M R) x}.

(25)

Rotation frequency decreases exponentially with increasing x(t). This follows from increasing of translational energy and instantaneous velocity v (see Figure 4):

E_trans = E₀ – E_rot

With (11) and (25) we get via E₀ = max E_rot = (1/4)M R² ω₀²

E_trans = (1/2) M'v² = (¼)M'R² ω₀² (1- exp {(-4mu/M R) x})

(26)

v² = (1/2)R² ω₀² (1- exp {(-4mu/M R) x})).

(27)

v = (1/2) ^½ R ω₀ (1- exp {(-4mu/M R) x}))^1/2

(28)

v(x) is instantaneous velocity in dependence of trajectory length x. Setting x = 0 delivers initial velocity v = 0 in accordance with our takeoff scenario above. From (28) we get by differentiation the instantaneous translational acceleration of the rotor:

a = (m_u /M´) R ω² = (m_u /M´)R ω₀² exp {(-4mu/M R) x})

(29)

Initial acceleration a ₀ follows from (29) by setting starting point condition x = 0:

a₀ = (m_u /M´) R ω₀²

(30)

Both, instantaneous acceleration a and velocity x, depend on mass quotient m_u /M´, which presents main steering magnitude for propulsion control. Acceleration increases proportional with m_u /M´.

4. Evaluation of UAV Flight Performance Data

Our theory above applies to the five parameters M, R, f, m_u, and C = M´/M. The radius R and masses M and M´ are assumed to be fixed parameters during flight which cannot be changed. The flight performance can be controlled by precisely adjusting the active unbalance mass m_u (or m_u/M) and/or by adjusting the initial rotation rate f₀ at the start (or the actual rotation rate f during flight). In most cases, a high initial rotation frequency f₀ is desired to store a large amount of energy on board, making the key steering parameter m_u/M.

Following formulas, derived above, are applied here for flight performance calculations:

# Energy mechanically stored E_rot = MR²ω₀²/4

(31)

This formula calculates the amount of pure mechanical energy stored in the system. Energy storable on board depends on square of radius R and square of rotation frequency f₀ and is proportional to mass M of the rotor. Any electrical power supply on board is ignored here.

There is no influence of construction factor C on magnitude of storable rotation energy.

# Initial thrust F'₀ = M' a'₀

(32)

This formula calculates the initial thrust generated by product of the mass of the vehicle (M') and its initial acceleration (a'₀)

# Initial acceleration a'₀ = (m_u /M') Rω₀².

(33)

determined by magnitude of m_u and/or rotation frequencyf₀. Typical values of

m_u = M´10^-4- M'^.10^-6 are assumed in calculation here, while f₀ is variable and R fixed by design.

# Height of vertex h_max = R²ω₀² g_E^-1.

(34)

Horizontal spin orientation of rotor disk has to be assumed here. Hight of vertex is independent from rotor mass M and m_u.

# Max. velocity v_max = R ω₀/2^1/2

(35)

Vertical spin orientation of rotor disk is assumed here. Maximum velocity is independent from rotor mass M and m_u.

For preliminary evaluation of potential in flight performance, we take here three hypothetical UAV´s of different size and mass and calculate height of vertex, initial thrust, initial acceleration and maximum velocity in dependance of initial rotation rate (Tables 1–4).

Tables 1–4: Flight performance data of different UAVs, calculated according Eq. (31)-(35) by means of hp 15C.

All data calculated here are obtained under the simplifying assumption M = M´, thus C = 1. For evaluation of a specific vehicle, we have to set its specific C >1. Thus, initial acceleration a' and initial trust F'₀ of the complete vehicle will be reduced, because of bigger vehicle mass M' compared to rotor mass M. This is according equation a M = a' M'= m_u R ω². For instance, assuming C = 2 the height of vertex as well as initial thrust of the vehicle are smaller, namely half value of the corresponding rotor data. Additionally, the way back to the earth surface and managing save landing needs energy, too. However, we see no serious limitation of the flight performance. Even the minirotor should reach considerable peak heights of several kilometers and more, depending on the starting rotational frequency f₀.

The medium-sized rotor should already reach flight altitudes of commercial aircraft at rotational speeds of 100 per second. With the heavy-sized rotor, heights and speeds should be achievable that promise orbital capabilities!

Increase of acceleration and inertial thrust is proportional to growing ω². In most cases the UAV user will not need really such high accelerations Thus, steering parameter mu/M can be reduced during start phase (for instance to 10^-6, see above the heavy sized rotor in human sized flight mode) and herewith rotational energy onboard can be saved for later maneuvers.

The performance increase of the bigger rotors is easy explained: The maximum height h_max of the rotor depends on the product of the squared radius R and the squared rotation frequency f₀, but h_max is independent of rotor mass M and steering parameter mu/M. Therefore, our theory says for instance, the vertex height of the heavy rotor will be about 256 times larger than the vertex height of the mini rotor, assuming same parameter values (m_u/M and f₀) for both rotors. Note, translational velocity depends also on the product R f₀, but linearly. Here, maximum velocity increases from 570 m/s (mini rotor) over 2,2 km/s (medium rotor) to 8,5 km/s (heavy rotor), all values calculated for top frequency 10³ /s.

We conclude here that controlled unbalance propulsion (CUP) of UAV´s could provide excellent flight performance data. Our calculations let us hope that high thrusts and vehicle velocities up to orbital levels could be achieved. Thus, working range of CUP-drones could be extended to near earth space and is not limited to earth atmosphere.

5. Maneuverability of the Rotor and Levitation in a Gravitational Field

Here, a distinction is made between two states: horizontal flight and vertical flight. The orientation of the rotor's axis of rotation at takeoff determines the flight state. Due to the principle of propulsion, the axis of rotation must always be perpendicular to the future plane of movement in which the translational displacement of the rotor will occur. Within this plane of movement, the flight direction is determined by the position of the rotor sector in which the unbalance is activated, specifically by the bisector of this rotor sector. This position can be adjusted through the electrical control of the unbalance and can therefore be easily changed. The new position of the bisector can be set within a single rotation of the rotor, if necessary, potentially in milliseconds. This allows for rapid changes in direction of the UAV within the x, y plane of movement (e.g., horizontal curved flight with a constant vertical axis direction). By reversing thrust, the aircraft can also decelerate (potentially with a subsequent change in flight direction) by electrically rotating the active rotor sector by 180 degrees relative to the previous direction of propulsion. In principle, no aerodynamic actuators are required to initiate these yaw and braking maneuvers.

During changes in attitude of a rotor-driven aircraft, gyroscopic forces can occur, which couple the movements around the aircraft's axes and their influence on the flight motion must be taken into account. Here is an example: After takeoff and before landing, it is necessary to tilt the rotor's axis of rotation by 90⁰ to transition from horizontal flight to vertical flight (or vice versa). This requires a rotation around the pitch axis, which is oriented perpendicular to the direction of propulsion and the vertical axis of rotation. In this transition phase, gyroscopic forces occur because the law of conservation of angular momentum opposes the change in direction. This also applies to rolling. Only in yawing (as described above) does the angular momentum remain directionally stable and disruptive gyroscopic forces cannot occur.

There are generally two methods for maneuvering under the influence of gyroscopic forces:

Utilization of gyroscopic forces
Compensation of gyroscopic forces.

The utilization of gyroscopic forces refers to the exploitation of the UAV's inertia moments to perform maneuvers. By deliberately changing the rotational speeds of the rotors, the UAV can be rotated around its longitudinal, lateral, and vertical axes. This allows for rolling, pitching, and yawing of the UAV. The compensation of gyroscopic forces refers to the mitigation of the undesirable effects of gyroscopic forces to ensure a stable flight attitude. This can be achieved through the use of sensors and control systems that adjust the rotational speeds of the rotors accordingly to compensate for unwanted rotations or vibrations. In our patent pending /10/, it is shown in detail how the maneuverability around all three axes of the UAV can be optimized. The patent specification demonstrates how these two methods can be combined to optimize the maneuverability of the UAV. By strategically utilizing gyroscopic forces and compensating for the undesirable effects, precise and stable maneuvers can be performed.

To find the rotational speed at which the centrifugal force compensates for the weight, we set:

m_u R (2πf) ² = M g_E

This leads to the hovering rotational speed:

f * = {(M g_E) / (4π² m_u R)}^1/2.

(36)

To calculate the specific frequency f*, let's substitute the given values for the medium rotor into the formula:

M = 10 kg, M = 10⁴ m_u (thus m_u = 1g), g_E = 9.81 m/s², R = 0.5 m

Substituting these values, we get:

f* = sqrt {(10⁴ m_u) 9.81m/s²) / (m_u^.0,5m ^.4π²)}

Calculating this, we obtain:

f* ≈ 70.5 Hz

Therefore, the desired frequency f* is approximately 70.5 Hz (or 4243 rpm).

We need to consider that even during the hovering of the rotor, its rotational energy is consumed because at least the center of mass M is displaced from the axis of rotation by the amount:

r = R m_u / M = 0.5m (10^-4) = 0.05 mm.

(37)

This displacement occurs exactly f* times per second during rotor operation.

To calculate the power consumed during the hovering of the rotor, we use the formula:

P = f * dE_rot.

(38)

With the energy loss dE_rot = M g_E r, we have:

P = f * M g_E r.

(39)

We substitute the given parameter values for the hovering medium rotor.

With 1 W = 1 kgm²/s³, the formula gives the power consumption in watts:

P = (70,5 Hz) (10 kg) (9.81 m/s² ) (0,05 10^-3 m) = 0,346 W

To calculate the time that the rotor can hover, we need to calculate the rotational energy reserve. The rotational energy E of a rigid body is given by the formula:

E = (1/2) θ ω²,

(40)

where θ is the moment of inertia and ω is the angular velocity. The moment of inertia of a cylinder (which is typically what a rotor is) is calculated using the formula:

θ = \frac{1}{2} M R^{2}

(41)

where M is the mass and R is the radius.

The angular velocity ω₀ is equal to 2πf₀, where f₀ = 400 Hz is the assumed starting frequency. Substituting the given values into the formulas:

θ = (1/2) 10 kg (0.5 m) ² = 1.25 kg m²

ω₀ = 2π 400 /s = 800π /s = 2,512 /s

Now we calculate the rotational energy:

E = (1/2) 1.25 kgm² (2512 /s)² = 3, 943, 840 J.

The time that the rotor can hover is then the stored rotational energy divided by the power:

t = E / P = 3,943,840 J/0,346 W = 11,398,381s. That's approximately 132 days.

(42)

This calculation is a strong simplification. In real rotor systems, additional factors such as friction, air resistance, and other losses can dominate and need to be taken into account, too.

6. Precise Control in Activating and Deactivating Rotor Unbalances

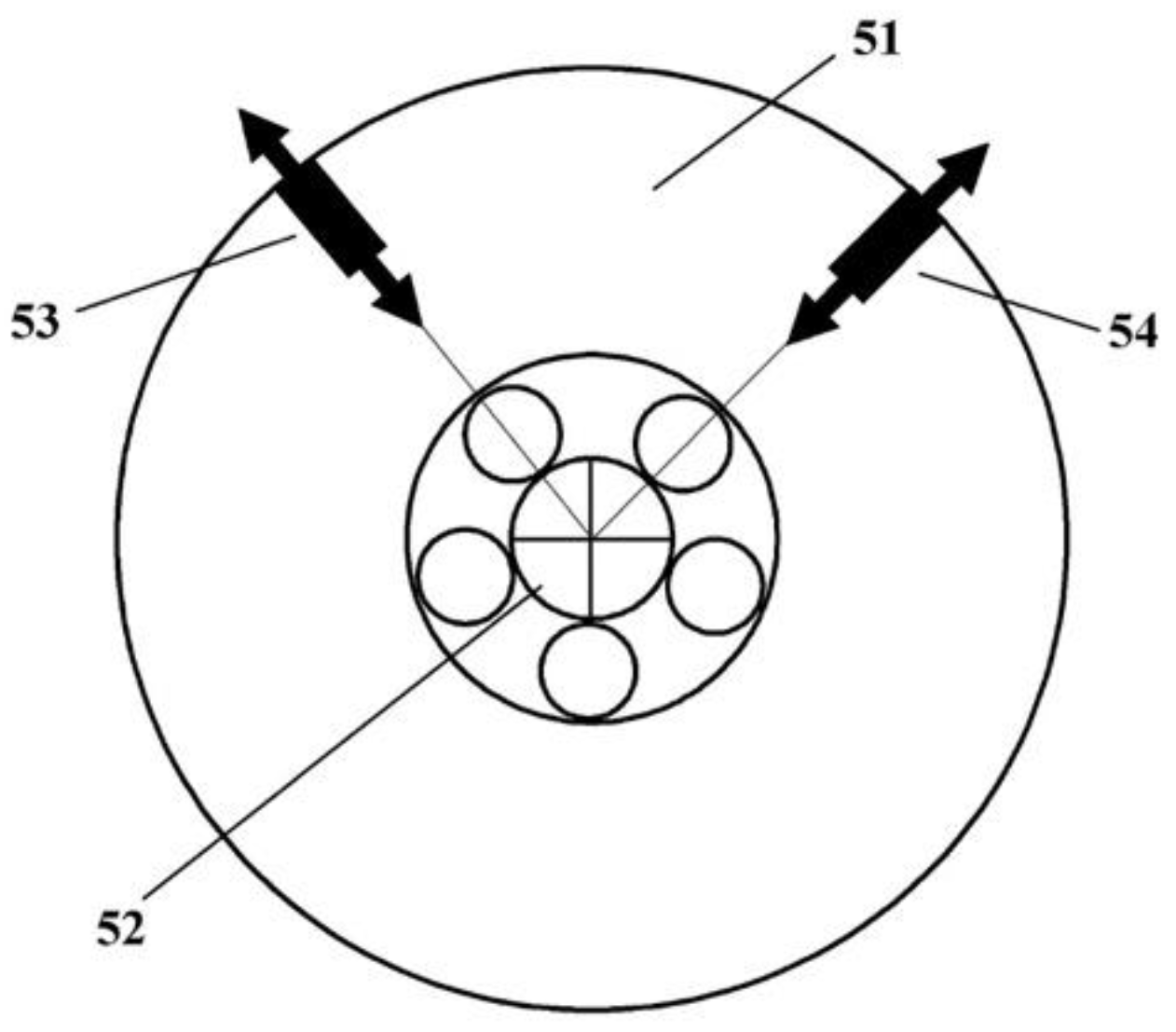
The timing and magnitude of the unbalance mass must be adjusted to optimize the propulsion generation. To achieve precise control of the unbalance mass, advanced control systems can be used. These systems monitor the rotational position of the rotor and activate electromechanical actuators to release or adjust the unbalance mass at the desired time and magnitude [11]. Electrically controllable actuators are fixed on the rotor which apply the piezoceramic length expansion effect (PCT) or the magnetostriktive length expansion effect. The local direction of the length expansion effect must be aligned with the local radial direction of the rotor, causing controlled mass displacement effects towards the rotor periphery and thus causing unbalance (Figure 5).

The characteristic feature in applying PCT is that the energy requirement for the permanent modulation of the piezoelectric unbalance generator is low because the generator can work highly powerless due to the high PCT internal resistance. Furthermore, the piezoelectric effect allows for rapid changes in unbalance. Possible PCT length changes are in the order of a few 100 µm, with mechanical response times of only 10^-4 s or less. The characteristic feature of the piezoelectric unbalance generator is that rotations with frequencies of 10 kHz and higher becomes technically possible. Therefore, we conclude that applying rotors equipped with current bearing technology the unbalance control could be realized up to rotor speeds of about 1000 rps, and even higher speeds are possible for magnetically levitated rotors. Note that during accelerated flight, only unbalance-induced inertial forces act on the rotor bearing, as the elastic support forces are eliminated when the rotor fixation is released. As a result, the load on the bearings due to unbalance is significantly smaller during flight compared to the operation of a tethered rotor. This is expected to have a favorable effect on the service life, especially for roller bearings.

7. High - Strength Rotor Materials

For highspeed rotors high tensile strength and low material density of the rotor material applied are essential. Designing a propulsion system, the following criterion of strength theory must be considered: In a high-speed rotating rotor (balanced), the tangential component of the surface stress s_t must not exceed the tensile strength of the rotor material:

s_t = ρ v²_R < maximum tensile strength s_max

(43)

The component of the surface stress s_t itself is proportional to the material density ρ and the square of the circumferential velocity v_R of the rotor. This is determined by:

v_R = 2πRf

(44)

Therefore, we have:

4π²f²R² < s_max

f R < (1/2π)(s_max/ρ) ^(1/2)

(45)

This formula says the optimized rotor material should have tensile strength s_max as large as possible and its density ρ should be as low as possible. Rotors build by using this optimized material allow large magnitudes of the critical product f R, i.e., high rotation frequencies f in combination with the large radius R of big sized rotors. Permissible tensile strength should include additional stresses by the centrifugal force of the unbalanced mass.

Our calculation results for some metallic materials and for carbon nanomaterials are shown in Figure 8. We draw following conclusion: Using present metallic rotor materials, radii in the sub-meter range can be achieved for speeds of 100-1000 rps, especially with carbon-fiber-reinforced polymer (CFRP) wrapped steel rotors, like described in [11]. Furthermore, based on some success in younger experiments with nano materials [11,12,13], single walled carbon nanotubes theoretically possess ultimate intrinsic tensile strengths in the 100 - 200 GPa range, among the highest in existing materials. We are so free to state here: The highest rotor speeds (1000 rps) could be achieved when using ultra-stabile carbon nanomaterial structures because this technology could be combined with allowable rotor radii in the order of several meters. Let us compare these demands to the state-of-the-art rotor equipment: CNC tool machine spindles (80 mm) make 250 rps, standard commercial high speed ball bearings perform 350 rps and magnetic bearings work up to 500.000 rpm and more, see [11,14].

Of course, there is always an alternative way in creating high thrust by means of pulse modulated force propulsion: Instead of a single super rotor with a large radius, a battery of several smaller rotors (mounted on a common vehicle platform) can be applied, operated with synchronous unbalance control so that the individual propulsion forces add up.

8. Final Conclusion

Pulsed centrifugal propulsion is based on well-established laws of physics, i.e., energy theorem, principle of linear and rotational momentum, and Newton´s axioms. We provide with traceable evidence that propulsion of small vehicles (UAV) can be generated by conversion of the rotational energy of airborne rotors. By precise setting/resetting unbalances during each rotor rotation short centrifugal force pulses can be induced and exactly directed. Thus, by controlled unbalance propulsion (CUP) the rotational energy of a rotor can be transformed into translational energy of the rotor carrying vehicle.

Furthermore, we conclude that controlled unbalance propulsion could provide excellent flight performance data of small UAV´s. Our calculations indicate that high thrusts and vehicle velocities up to orbital levels could be achieved. Thus, working range of high-performance CUP-drones could be extended to near earth space and seems not limited to earth atmosphere. Additionally, exceptional maneuverability and levitation can be attained making these UAVs superior to conventional drones. Targeted action in the design and performance dimensioning of centrifugal force drives is possible based on this information. This paper allows for specific actions to be taken when designing and determining the performance of centrifugal force drives.

Last but not least, a second CUP generation applying combined inertial/electric propulsion of vehicles appears to be feasible. Here the unbalance-controlled rotor is part of an electric motor drive/generator circuit. Initially, additional electrical power is stored in (low weight) onboard batteries during the prestart phase. This process occurs in parallel with the electrical loading of the rotor to its maximum rotation frequency, ω₀. Later, during flight, the stored electrical energy can be used to compensate for the decrease in rotational energy during the vehicle's thrust phases. This allows the rotor to maintain a constant frequency, ω₀, during vehicle operation, which should simplify the guidance software and energy management. Furthermore, due to the increase in total onboard energy, the operational range of the vehicle should be expanded.

Funding

This research received no external funding.

References

Bowen Zhang, Zaixin Song, Fai Zhao, Chunhua Liu "Overview of Propulsion Systems for Unmanned Aerial Vehicles" Energies 2022, 15(2),455; Published: 10 January 2022. [CrossRef]
Dhawal Joshi, Dipankar Deb, SM Muyeen "Comprehensive Review on Electric Propulsion System of Unmanned Aerial Vehicles" Front. Energy Res., 14 May 2022 Sec. Smart Grids Volume 10 - 2022 | . [CrossRef]
2020; 3. "Drone - Unmanned Aerial Vehicle (UAV)" 2020-2023 Safe Drones over Save Environment Tempus Foundation Erasmus + 2020-1-RS01-KA202-065370 HANDBOOK.
US Patent 2018 000551A1: "Impulse Momentum Propulsion Apparatus and Method" by James F. Woodward (2018).
": 4,663,932, 1987; 4, 5. US-Patent 4,663,932: "Gyroscopic Propulsion" by Henry William Wallace (1987).
": 4,238,968, 1980; 4, 6. US-Patent 4,238,968: "Gyroscopic Propulsion Device" by Sandy Kidd (1980).
US-Patent 3,182,517: "Propulsion System" by Norman L. Dean (1965).
Wikipedia contributors. (2024, January 5). "Flywheel energy storage". In Wikipedia, The Free Encyclopedia. Retrieved 09:46, March 10, 2024, from https://en.wikipedia.org/w/index.php?title=Flywheel_energy_storage&oldid=1193758748.
"Flywheel -Generators" Max Planck Institute for Plasma Physics, 2021. https://www.ipp.mpg.de ›generator.
Buchroithner A. "Flywheel Energy Storage in Automotive Engineering" Springer 2023 p. 327 ISBN-10 ‏: 3658353414 ISBN-13 ‏: 978-3658353414.
Bai,Y., Zhang, R.,et al. "Carbon nanotube bundles with tensile strength over 80 GPa" Nature Nanotech. 13, 589-595 (2018). [CrossRef]
Takakura, A., Beppu, K., Nishihara, T. et al. "Strength of carbon nanotubes depends on their chemical structures". Nat. Commun. 10, 3040 (2019). [CrossRef]
Ruoff, R.S." Strong bundles based on carbon nanotubes". Nature Nanotech 13, 533-534 (2018). [CrossRef]
Schuck, M.; Steinert D.; Nussbaumer T.; Kolar J. "Ultrafast rotation of magnetically levitated macroscopic steel spheres" Science Advances Vol 4, No.1 (2018). [CrossRef]
Cambridge Engineering Selector software (CES 4.1), 2003, Granta Design Limited, Rustat House, 62 Clifton Rd, Cambridge, CB1 7EG (Materials Data).
"Verfahren zur Vortriebserzeugung" Wolfgang Holzapfel Patent pending DE 10 2021 004 170 A1 2023.02.16, Deutsches Patent- und Markenamt.

Figure 1. left: Unbalanced rotor due to asymmetric mass distribution. right: equivalent circuit mass point diagram with A rotation axis, perpendicular to paper plane (x;y), m_u point of unbalance mass, M point of rotor disc mass, R rotor radius, r translation of M due to m_u.

Figure 2. Components of centrifugal force vector.

Figure 3. Active angle interval 2α_x.

Figure 4. Decrease of rotational energy E_rot and increase of translational energy E_trans in dependence of flight path length x(t). E₀, E_1/2 max and half-max of rotation energy, A* Point of energetic equivalence.

Figure 5. Actuatoric generation of rotor unbalance (application example) 51 rotor disc, 52 rotor bearing, 53 and 54 unbalance actuators, both rotor fixed.

Figure 8. Highest rotation frequencies f₀/s in dependence of radius R and parameter s_max/ ρ for selected materials according to Eq. (45), material data according [11,12,13,14,15,16].

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.