Preprint

Article

Enhanced Linear and Vision Transformer-Based Architectures for Time Series Forecasting

Altmetrics

Downloads

180

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 April 2024

Posted:

16 April 2024

You are already at the latest version

Alerts

Abstract

Time series forecasting has been a challenging area in the field of Artificial Intel-ligence. Various approaches such as linear Neural Networks, Recurrent Linear Neural Networks, Convolutional Neural Networks and recently Transformers have been attempted for the time series forecasting domain. Although, Trans-former-based architectures have been outstanding in the Natural Language Pro-cessing domain, especially in autoregressive language modeling, the initial at-tempts to use transformers in the time series arena have met with mixed success. One of the recent papers demonstrated that modeling the multi-variate time se-ries problem as independent channels on a transformer architecture produced lower mean square and mean absolute errors on benchmarks, however, another recent paper claimed that a simple linear neural network out-performs previous approaches including transformer-based designs. We investigate this paradox in detail comparing the linear Neural Network and Transformer based designs, provide insights to why a certain approach may be better for a particular type of problem. We also improve upon the recently proposed simple linear Neural Network based architecture by using dual pipelines with batch normalization and reversible instance normalization. Our enhanced architecture outperforms all existing architectures for time series forecasting on majority of the popular benchmarks.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The goal of time series forecasting is to predict future values based on patterns observed in historical data. It has been an active area of research with applications in many diverse fields such as weather, financial markets, electricity consumption, health care, and market demand among others. Over the last few decades, different approaches have been developed for time series prediction involving classical statistics, mathematical regression, machine learning, and deep learning-based models. Both univariate and multivariate models have been developed for different application domains. The classical statistics and mathematics based approaches include moving average filters, exponential smoothing, Autoregressive Integrated Moving Average (ARIMA), SARIMA [1] and TBATs [2]. SARIMA improves upon ARIMA by also taking into account any seasonality patterns and usually performs better in forecasting complex data containing cycles. TBATs further refines SARIMA by including multiple seasonal periods.

With the advent of machine learning where the foundational concept is to develop the model that learns from data, several approaches to time series forecasting have been explored including Linear Regression, XGBoost, and Random Forests. Using Random forests or XGBoost for time series forecasting requires the data to be transformed into a supervised learning problem using a sliding window approach. When the training data is relatively small, the statistical approaches tend to yield better results. However, it has been shown that for larger data, machine learning approaches tend to outperform the classical mathematical techniques of SARIMA and TBATs [3].

In the last decade, deep learning-based approaches to time series forecasting have drawn considerable research interest starting from designs based on Recurrent Neural Networks (RNNs) [4,5]. A detailed study comparing the ARIMA based architectures and RNNs [5] concluded that RNNs can model seasonality patterns directly if the data has homogeneous seasonal patterns; otherwise, a deseasonalization step was recommended. It was also concluded that (semi-) automatic RNN models are no silver bullets but can be competitive in some situations. The work in [5] compared different RNN designs and indicated that Long Short Term Memory (LSTM) cell with peephole connections performed relatively better, the Elmann Recurrent Neural Network (ERNN) cell performed the worst, and the performance of the Gated Recurrent Unit (GRU) was in between.

LSTM and Convolutional Neural Networks (CNNs) have been combined together to address the long term and short term patterns arising in data. One notable design was proposed in [6] termed by the authors as Long- and Short-term Time-series network (LSTNet). It uses the CNN and RNN to extract short-term local dependency patterns among variables and to discover long-term patterns for time series trend. Recently, use of RNNs and CNNs is being replaced by Transformer-based architectures in many applications such as Natural Language Processing (NLP) and Computer Vision. Transformer [7] which uses attention mechanism to determine the similarity in the input sequence is one of the best models for NLP applications as demonstrated by the success of Large Language Models such as ChatGPT. Some time series forecasting implementations using Transformers have achieved good performances [8,9,10]. However, the Transformer has some inherent challenges and some limitations with respect to time series forecasting in current implementations due to the following reasons:

Temporal Dynamics vs. Semantic Correlations: Transformers excel in identifying semantic correlations but struggle with the complex, non-linear temporal dynamics crucial in time series forecasting [11,13]. To address this , an auto-correlation mechanism is used in Autoformer [9].
Order Insensitivity: The self attention mechanism in Transformers treats inputs as an unsequenced collection, which is problematic for time series prediction where order is important. Even though, positional encodings used in Transformers partially addresses this but may not fully incorporate the temporal information. Some transformer-based models try to solve this problem using enhancements in architecture, e.g., Autoformer [9] uses series decomposition blocks that enhance the system's ability to learn from intricate temporal patterns [9,13,14]
Complexity Trade-offs: The attention mechanism in Transformers has high computational costs for long sequences due to its quadratic complexity $O (L^{2})$ , and while modifications of sparse attention mechanisms e.g., Informer [8] reduces this to $O (L \times l o g (L))$ by using a ProbSparse technique. Some models reduce this complexity to $O (L)$ e.g., FEDformer [15] that uses Fourier enhanced structure, and Pyraformer [16] which incorporates pyramidal attention module with inter-scale and intra-scale connections to accomplish the linear complexity. These reductions in complexity come at the cost of some information loss in the time series prediction.
Noise Susceptibility: Transformers with many parameters are prone to overfitting noise, a significant issue in volatile data like financial time series where the actual signal is often subtle [13].
Long-Term Dependency Challenge: Transformers, despite their theoretical potential, often find it challenging to handle very long sequences typical in time series forecasting, largely due to training complexities and gradient dilution. For example, PatchTST [11] used disassembling a time series into smaller segments and used it as patches to address this issue. This may cause some segment fragmentation issues at the boundaries of the patches in input data.
Interpretation Challenge: Transformers' complex architecture with layers of self-attention and feed-forward networks complicates understanding their decision-making, a notable limitation in time series forecasting where rationale clarity is crucial. An attempt has been made in LTS-Linear [13] to address this by using a simple linear network instead of a complex architecture. However, this may be unable to exploit the intricate multivariate relationships between data.

2. Related Work

Some of the recent works related to time series forecasting include models based on simple linear networks, transformers and state space models. One of the important works related to Long Term Time Series Forecasting (LTSF) termed as LTSF-Linear was presented in [13]. It uses the most fundamental Direct Multi-Step DMS [17] model through a temporal linear layer. The core approach of LTSF-Linear involves predicting future time series data by directly applying a weighted sum to historical data as shown in Figure 1.

The output of LTSF-Linear is described as:

{\hat{X}}_{i} = {W X}_{i}

, where

W \in R^{T \times L}

is a temporal linear layer and

X_{i}

is the input for the

i^{t h}

variable. This model applies uniform weights across various variables without considering spatial correlations between the variates. Besides LTSF-Linear, a few variations termed as NLinear and DLinear were also introduced in [13]. NLinear processes the input sequence through a linear layer with normalization by subtracting and re-adding the last sequence value before predicting. DLinear decomposes raw data into trend and seasonal components using a moving average kernel, processes each with a linear layer, and sums the outputs for the final prediction [13]. This concept has been borrowed from the AutoFormer and FedFormer models [9,10].

Although some research indicated success of the transformer-based models for time series forecasting e.g., [8,9,10,16], the LTSF-Linear work in [13] questioned the use of transformers due to the fact that the permutation-invariant self-attention mechanism may result in temporal information loss. The work in [13] also presented better forecasting results than the previous transformer-based approaches. However, an important research later presented in [11] proposed a transformer-based architecture called PatchTST showing better results than [13] in some cases. PatchTST segments the time series into subseries-level patches and maintains channel independence between variates. Each channel contains a single univariate time series that shares the same embedding and transformer weights across all the series. Figure 2 depicts the architecture of PatchTST.

In PatchTST, the i_th series for L time steps is treated as a univariate

x_{1 : L}^{i} = (x_{1}^{(i)}, \dots, x_{L}^{(i)})

. Each of these is fed independently to the Transformer backbone after converting to patches, which provides prediction results

\hat{x} = ({\hat{x}}_{L + 1}^{(i)}, \dots, {\hat{x}}_{L + T}^{(i)}) \in R^{1 \times T}

for T future steps. For a patch length P and stride S, the patching process generates a sequence of N patches

x_{p}^{(i)} \in R^{P \times N}

where

N = ⌊\frac{(L - P)}{S}⌋ + 2

. With the use of patches, the number of input tokens can reduce to approximately

L / S

Recently State Space Models (SSMs) have received considerable attention in the NLP and Computer Vision domain [18,19]. For time series forecasting, it has been reported that SSM representations cannot express autoregressive processes effectively. An important recent work using SSM is presented in [20] (termed as SpaceTimeSSM) that enhances the traditional SSM model by employing a companion matrix which enables SpaceTime’s SSM layers to learn desirable autoregressive processes. The time series forecasting represents the input series for p past samples as:

u_{k} = \emptyset_{1} u_{k - 1} + \emptyset_{2} u_{k - 2} + \dots . \emptyset_{p} u_{k - p}

(1)

Then the state space formulation is given as:

x_{k + 1} = {A x}_{k} + {B u}_{k}

(2)

y_{k + 1} = {C x}_{k + 1} + {D u}_{k}

(3)

y_{k + 1} = u_{k + 1} = C ({A x}_{k} + {B u}_{k})

(4)

The SpaceTimeSSM composes the companion matrix A as a dxd square matrix:

A = [\begin{matrix} \begin{matrix} 0 0 \dots 0 a_{0} \\ 1 0 \dots 0 a_{1} \\ 0 1 \dots 0 a_{2} \end{matrix} \\ ⋮ ⋱ ⋮ ⋮ \\ 0 1 \dots 0 a_{d - 1} \end{matrix}]

(5)

where

a : = {[a_{0} a_{1} \dots a_{d - 1}]}^{T} = 0, B = {[1 0 \dots 0]}^{T}, C

[\emptyset_{1} \dots \emptyset_{p}]

We provide comparison of different time series benchmarks on the SpaceTimeSSM approach in the results section.

3. Methodology

3.1. Proposed Models for Time Series Forecasting

As explained in the previous related works section, there are three competing approaches for time series forecasting: one based on simple linear networks, the second based on transformers where the input series is converted to patches and channel independence is claimed to be a better scheme, and the third approach based on state space models with additional enhancements to incorporate autoregressive behavior. We investigate these approaches further to see if better models for time series can be created in at least the first two categories. In the next subsections, we elaborate our enhancements on existing linear and transformer-based approaches.

3.2. Enhanced Linear Models for Time Series Forecasting (ELM)

We enhance the LTSF-Linear approach presented in [13] by performing a batch normalization and reversible instance normalization. We further combine the information in a novel way using a dual pipeline design as shown in Figure 2. The recent important works e.g., LTSF-Linear [13] that is based on simple linear networks, and the PatchTST work in [19] based on transformers emphasized channel independence produces better results. We maintain this attribute but further augment the linear architecture with batch normalization. This stabilizes the distribution of input data by normalizing the activations in each layer. It also allows for higher learning rates and reduces the need for strict initialization and some forms of regularization such as dropout. By addressing the internal covariate shift, batch normalization improves network stability and performance across various tasks.

While one of the enhancements in [13] termed as NLinear accommodated for distribution shift in the dataset by subtracting the last value of the sequence, and then adding it back after the linear layer, before doing the final prediction, we incorporate a similar idea in our architecture as a separate stream as shown in Figure 3.

One difference in our implementation for the distribution shift is that we further add a batch normalization to combine temporal information more effectively. From Figure 3, it can be seen that there are two distinct pipelines operating on the input sequence in the beginning. These two streams are then merged together with the values being averaged, and after passing through a non-linearity (GeLU) and another batch normalization layer, we pass through a final Reversible Instance Normalization layer (RevIn). The RevIn originally proposed in [21] operates on each channel of each variate independently. It applies a learnable transformation to normalize the data during training, such that it can be reversed to its original scale during prediction.

We also use a custom loss function that combines the L2 (MSE) and L1 (MAE) losses together in a weighted manner as described below.

L o s s = α \times {‖y - \hat{y}‖}_{2} + (1 - α) {‖y - \hat{y}‖}_{1}

(6)

where α is a weighting factor between 0 and 1. MSE (input, target) calculates the mean squared error between the input and target values. L1(input, target) calculates the mean absolute difference between the input and target values. As demonstrated in our results section, our enhanced linear networks-based architecture produces better results than existing approaches in many cases on different benchmarks.

3.3. Adaptation of Vision Transformers to Time Series Forecasting

While one of the recent works on time series forecasting used simple transformer-based architecture (PatchTST [11] ) with channel independence, we explore a more intricate transformer architecture i.e., Swin transformer [22]. The Swin Transformer presents an innovative and streamlined structure for vision-related tasks through the utilization of shifted windows to compute representations. This method tackles the scalability issues inherent to transformers in vision applications by ensuring a linear computational complexity that correlates with the size of the image. It has the additional advantage of overcoming the information loss in the patching process by the use of hierarchical overlapping windows. As a result, it has demonstrated superior results across various computer vision applications. Due to these inherent advantages of the Swin architecture, we adapt it to the time series forecasting domain. We treat the multivariate input series

\in R^{L \times d}

with

L

past steps and d channels as an

L \times d

image and convert it to appropriate number of patches that are then fed to the Swin model. Due to the use of overlapping, shifted and hierarchical windows, it has the potential for learning better cross-channel information in predicting the future time series data. The architecture of our Swin-based time series model is shown in Figure 4.

For feeding the multivariate time series

\in R^{d \times L}

with

L

time steps and d variates to the Swin transformer, the input data needs to be converted to

n^{2}

patches where

n

is a power of 2. We accomplish this by creating

n^{2} = \frac{(d \times L) - r}{k}

number of patches where

r

and

k

are integers which are selected to convert the input data to

n^{2}

patches. For example, if the input series data has 512 time steps with 7 channels, then

k = 14

and

r = 0

. This results in 256 patches i.e.,

n = 256

. We present the evaluation results on different benchmarks in the next section.

4. Results

We test our architectures and perform analyses on nine widely used datasets from real-world applications. These datasets consist of the Electricity Transformer Temperature (ETT) series, which include ETTh1 and ETTh2 (hourly intervals), and ETTm1 and ETTm2 (5-minute intervals), along with datasets pertaining to Traffic (hourly), Electricity (hourly), Weather (10-minute intervals), Influenza-Like Illness (ILI) (weekly), and Exchange Rate (daily). The characteristics of the different datasets used are summarized in Table 1.

The architecture types of models that we compare to our approach are listed in Table 2.

Table 3 shows the detailed results for our Enhanced Linear Model (ELM) on different datasets and compares it with other recent popular models.

As can be seen from Table 3, our ELM model surpasses most established baseline methods in majority of the test cases (indicated by bold values). The underline values in Table 3 indicate the second best results for a given category. Our model is either the best or the second best in most categories. Note that each model in Table 3 follows a consistent experimental setup, with prediction lengths T of {96, 192, 336, 720} for all datasets except for the ILI dataset. For the ILI dataset, we use prediction lengths of {24, 36, 48, 60}. For our ELM model, the look-back window L is 512 for all datasets except Exchange and Illness which use L= 96. For the other models that we compare to, we select their best prediction based on look-back window size from either of the (96, 192, 336, 720) [11,13]. Metrics used for evaluation are MSE (Mean Squared Error) and MAE (Mean Absolute Error).

Figure 5 and Figure 6 show the graphs of predicted vs. actual data for two of the datasets with different prediction lengths using a context length of 512 for our ELM model for the first channel (pressure for the weather dataset, and HUFL - high useful load for the ettm1 dataset). As can be seen, if the data is more cyclical in nature (e.g., HUFL in ettm1), our model is able to learn the patterns nicely as shown in Figure 6. For complex data such as pressure feature in weather, the prediction is less accurate as indicated in Figure 5.

Table 4 presents our results on the Swin transformer-based implementation for time series. As explained earlier, we divide the input multivariate time series data into 16x16 i.e., 256 patches before feeding it to a Swin model with three transformer layers. The embeddings used in the three layers are [128, 128, 256]. As can be seen that the Swin transformer-based approach which has inherent capability to combine information between different channels as well as between different time-steps does not perform as well as our linear model (ELM). Only, on the traffic dataset, it produces the best result. This could be attributed to the fact that this dataset has the most number of features that Swin can effectively use more cross-channel information. Comparing our Swin transformer-based model to the PatchTST model [11] (also transformer based), the PatchTST that uses channel independence performs better than our Swin-based model. Note that the PatchTST performs worse than our ELM model that is based on linear network.

We also compare our ELM model to the newly proposed State Space Model based time series prediction [20]. State Space Models such as Mamba [18] , VMamba [19] and Time-Machine Mamba [23] are drawing significant attention for modeling temporal data such as time series, and therefore we compare our ELM model with the recently published work of [20] and [23] that are based on State Space models. Table 5 shows the results of our ELM model with the work in [20,23]. In one case, the SpaceTime model is better but for most of the time, our ELM model performs better than both the State Space and the previous DLinear models. The context length in Table 5 is 720, and the prediction is also 720 time steps.

5. Discussion

One of the recent unanswered questions in time series forecasting has been as to which architecture is best suited for this task. Some earlier research papers have indicated better results with transformer-based models than previous approaches e.g., Informer [8], Autoformer [9] and Fedformer [10], Pyraformer [16]. Of these models, FedFormer demonstrated much better results as it uses Fourier enhanced blocks and Wavelet enhanced blocks in the transformer structure that can learn important patterns in series through frequency domain mapping. A simpler transformer-based architecture yielding even better results was proposed in [11]. This architecture termed as PatchTST used independent channels where an input channel is divided into patches. All channels share the same embedding and transformer weights. Since PatchTST is a simple transformer design with a simple independent channel architecture, we explored replacing this design with a Swin transformer with patching across channels. The Swin transformer has the capability to combine information across patches due to its hierarchical overlapping window design. Our detailed experimental results on the Swin architecture-based design did not produce better results as compared to the channel independent design of PatchTST, however, compared with other transformer-based designs, it did yield improved results in many cases.

To answer the question of the best architecture for time series forecasting, we improve the recently proposed simple linear network based model in [13] by creating dual pipelines with batch and reversible instance normalizations. We maintain channel independence and our results on the benchmarks show the best results obtained so far as compared to existing approaches in majority of the standard datasets used in time series forecasting.

6. Conclusions

We perform a detailed investigation as to the best architecture for time series forecasting. We have implemented time series forecasting on the Swin transformer to see if aggregated channel information is useful. We also analyzed and improved an existing simpler model based on linear networks. Our study highlights the significant potential of simpler models, challenging the prevailing emphasis on complex transformer-based architectures. The ELM model developed in this work, with its straightforward design, has demonstrated superior performance across various datasets, underscoring the importance of re-evaluating the effectiveness of simpler models in time series analysis. Only when the number of variates in the dataset is large, the Swin transformer-based design seem to be effective.

Our future work involves the development of hybrid models that leverage both linear and transformer elements such that each contributes to the effective learning of the time series behavior. For example, the frequency domain component as used in FedFormer could aid a linear model when past periodicity pattern is more complex.

References

G. E. Box, G. M. Jenkins, G. C. Reinsel, and G. M. Ljung, “Time series analysis: forecasting and control,” John Wiley & Sons, 2015.
De Livera, A.M., Hyndman, R.J., & Snyder, R. D. (2011), Forecasting time series with complex seasonal patterns using exponential smoothing, Journal of the American Statistical Association, 106(496), 1513-1527. [CrossRef]
Vitor Cerqueira1,, Luis Torgo1, and Carlos Soares1, "Machine Learning vs Statistical Methods for Time Series Forecasting: Size Matters," arXiv:1909.13316v1 [stat.ML] 29 Sep 2019.
David Salinas, Valentin Flunkert, Jan Gasthaus, Tim Januschowski, “DeepAR: Probabilistic forecasting with autoregressive recurrent networks,” International Journal of Forecasting, Volume 36, Issue 3, 2020, Pages 1181-1191, ISSN 0169-2070. [CrossRef]
Hansika Hewamalage, Christoph Bergmeir, Kasun Bandara, “Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions,” International Journal of Forecasting Volume 37, Issue 1, January–March 2021, Pages 388-427.
Guokun Lai, Wei-Cheng Chang, Yiming Yang, Hanxiao Liu, "Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks," SIGIR 18, July 2018.
Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. "Attention is all you need." Advances in neural information processing systems 30 (2017).
Zhou, Haoyi, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, and Wancai Zhang. "Informer: Beyond efficient transformer for long sequence time-series forecasting." In Proceedings of the AAAI conference on artificial intelligence, vol. 35, no. 12, pp. 11106-11115. 2021.
Wu, Haixu, Jiehui Xu, Jianmin Wang, and Mingsheng Long. "Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting," Advances in Neural Information Processing Systems 34 (2021): 22419-22430.
Zhou, Tian, Ziqing Ma, Qingsong Wen, Xue Wang, Liang Sun, and Rong Jin. "Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting." In International Conference on Machine Learning, pp. 27268-27286. PMLR, 2022.
Nie, Yuqi, Nam H. Nguyen, Phanwadee Sinthong, and Jayant Kalagnanam. "A Time Series is worth 64 words: Long-term forecasting with Transformers," arXiv preprint arXiv:2211.14730 (2022).
Zhou, Haoyi, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, and Wancai Zhang. "Informer: Beyond efficient transformer for long sequence time-series forecasting." In Proceedings of the AAAI conference on artificial intelligence, vol. 35, no. 12, pp. 11106-11115. 2021.
Zeng, Ailing, Muxi Chen, Lei Zhang, and Qiang Xu. "Are Transformers effective for Time Series Forecasting?." In Proceedings of the AAAI conference on artificial intelligence, vol. 37, no. 9, pp. 11121-11128. 2023.
Li, Shiyang, Xiaoyong Jin, Yao Xuan, Xiyou Zhou, Wenhu Chen, Yu-Xiang Wang, and Xifeng Yan. "Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting." Advances in neural information processing systems 32 (2019).
Zhou, Tian, Ziqing Ma, Qingsong Wen, Xue Wang, Liang Sun, and Rong Jin. "Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting." In International Conference on Machine Learning, pp. 27268-27286. PMLR, 2022.
Shizhan Liu, Hang Yu, Cong Liao, Jianguo Li, Weiyao Lin, Alex X Liu, and Schahram Dustdar, “Pyraformer: Low-complexity pyramidal attention for long-range time series modeling and forecasting,” International Conference on Learning Representations, 2022.
Chevillon, Guillaume. "Direct multi-step estimation and forecasting," Journal of Economic Surveys 21, no. 4 (2007): 746-785.
Gu, Albert, and Tri Dao. "Mamba: Linear-time sequence modeling with selective state spaces." arXiv preprint arXiv:2312.00752 (2023).
Liu, Yue, Yunjie Tian, Yuzhong Zhao, Hongtian Yu, Lingxi Xie, Yaowei Wang, Qixiang Ye, and Yunfan Liu. "Vmamba: Visual state space model." arXiv preprint arXiv:2401.10166 (2024).
Michael Zhang, Khaled Saab, Michael Poli, Tri Dao, Karan Goel, and Christopher Ré, "Effectively Modeling Time Series with Simple Discrete State Spaces," arXiv:2303.09489v1 [cs.LG] 16 Mar 2023.
Kim, Taesung, Jinhee Kim, Yunwon Tae, Cheonbok Park, Jang-Ho Choi, and Jaegul Choo. "Reversible instance normalization for accurate time-series forecasting against distribution shift," International Conference on Learning Representations, 2021.
Liu, Ze, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and Baining Guo," Swin transformer: Hierarchical vision transformer using shifted windows," Proceedings of the IEEE/CVF international conference on computer vision, pp. 10012-10022. 2021.
Ahamed, Md Atik, and Qiang Cheng. "TimeMachine: A Time Series is Worth 4 Mambas for Long-term Forecasting." arXiv preprint arXiv:2403.09898 (2024).

Figure 1. Temporal Linear Network in LTSF-Linear [13].

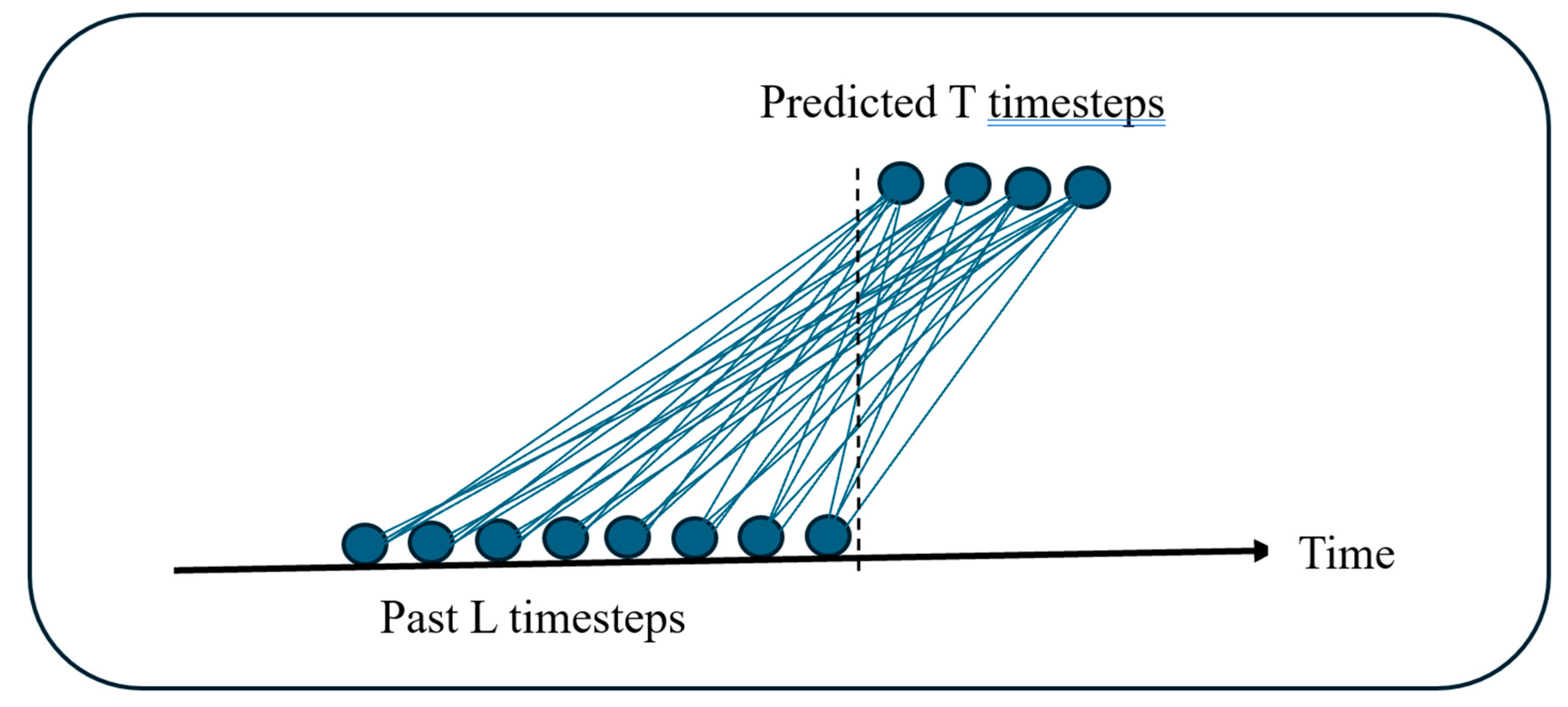
Figure 2. Architecture of PatchTST [13].

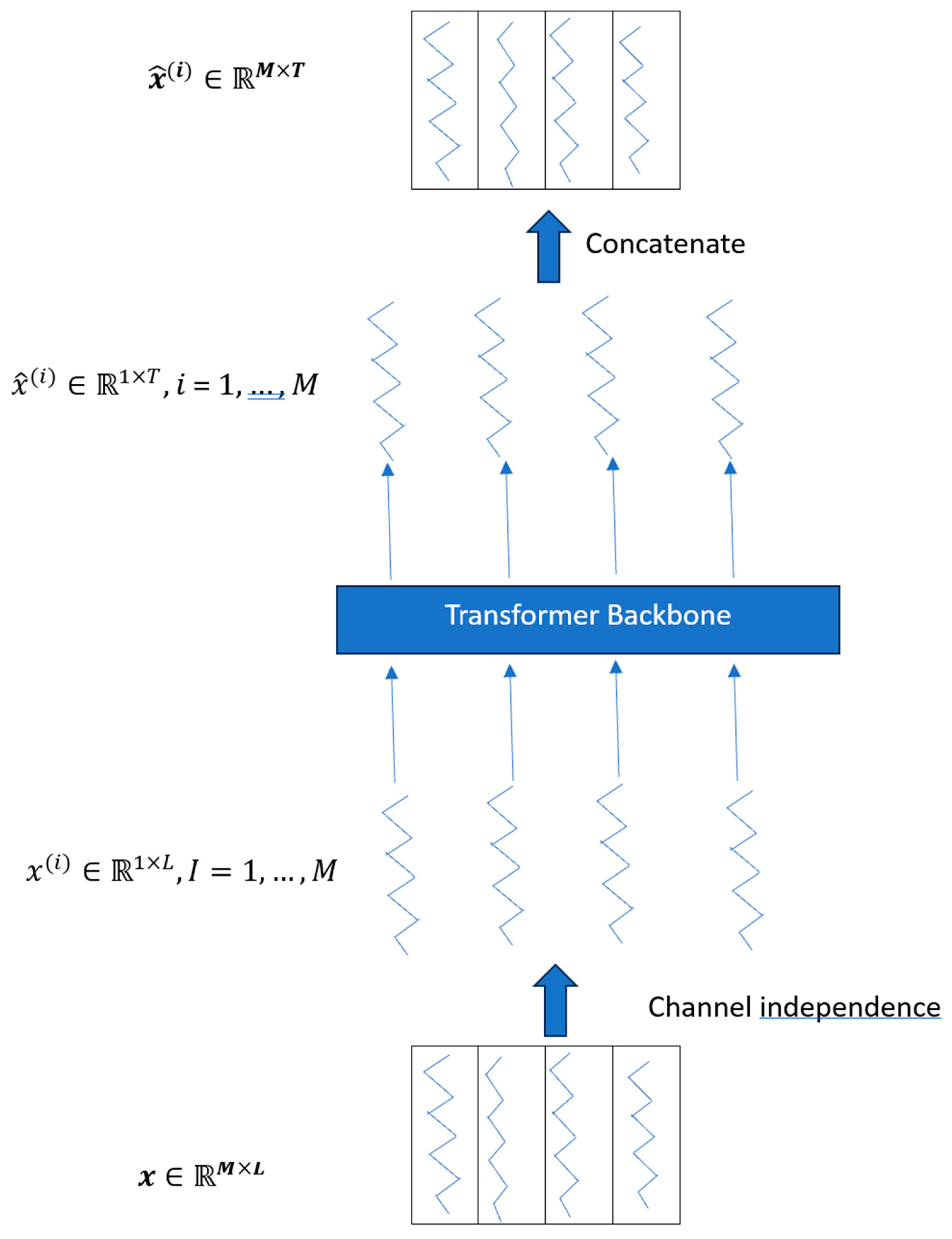
Figure 3. Our Enhanced Linear Model (ELM).

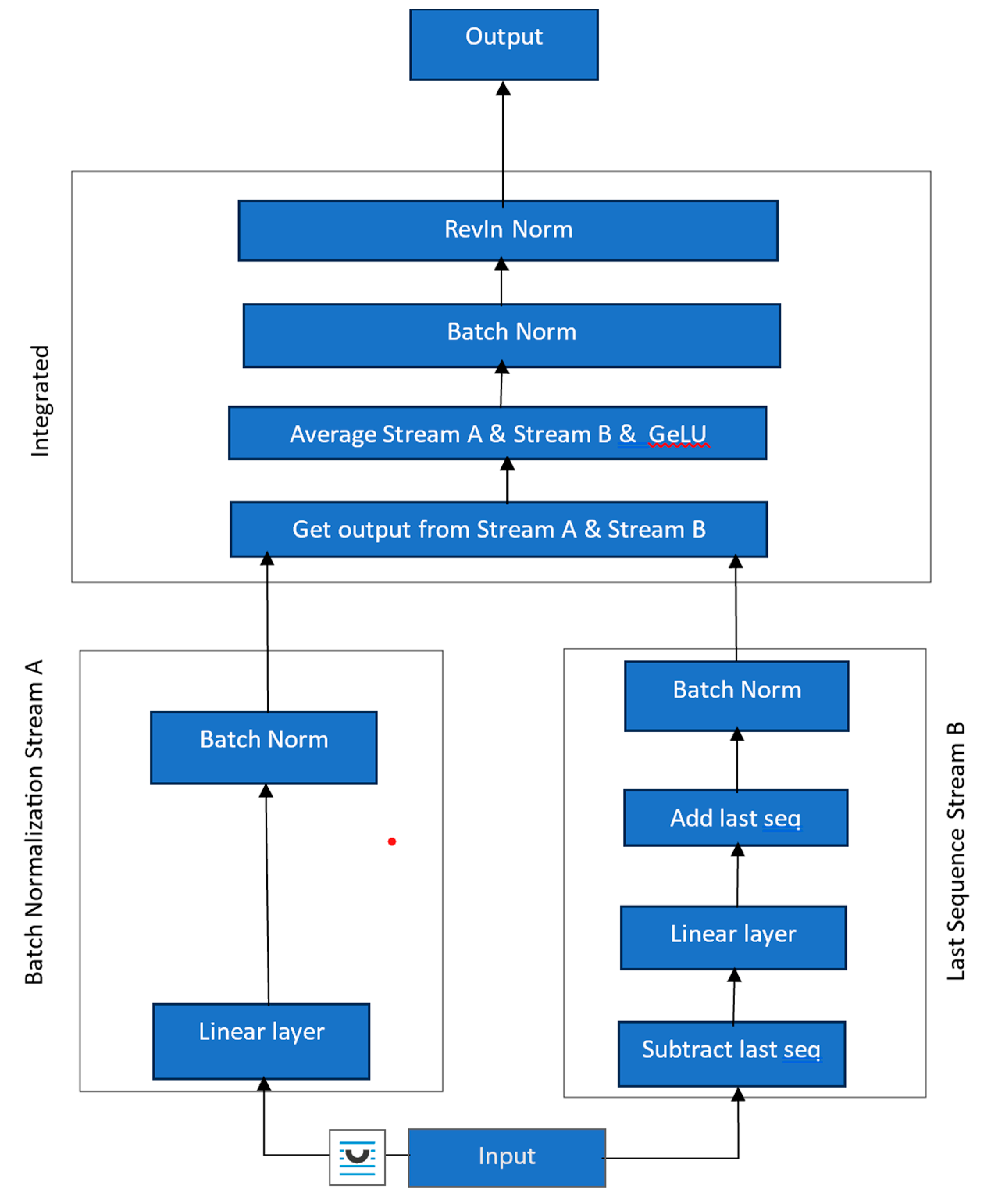
Figure 4. Adaptation of Swin Transformer Architecture for Time Series Forecasting.

Figure 5. Predicted vs. Actual forecasting using ELM Model with L= 512 and T = {96, 720} for weather dataset.

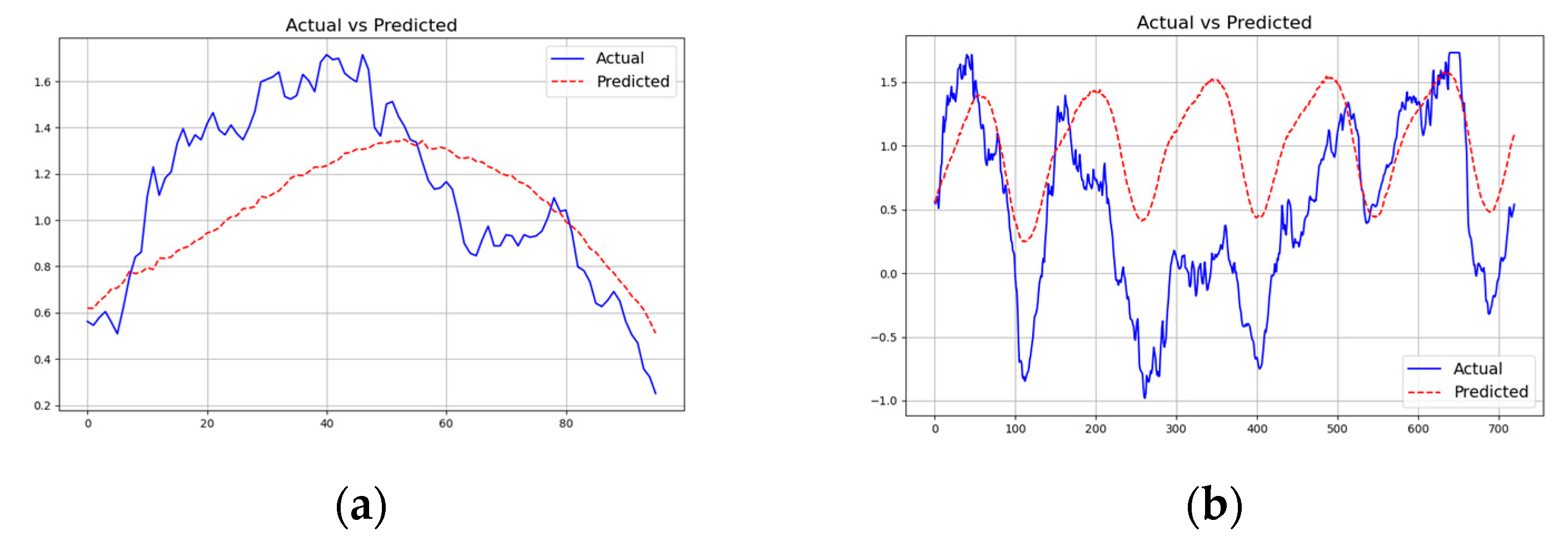
Figure 6. Predicted vs. Actual forecasting using ELM Model with L= 512 and T = {96, 720} for ettm1 dataset.

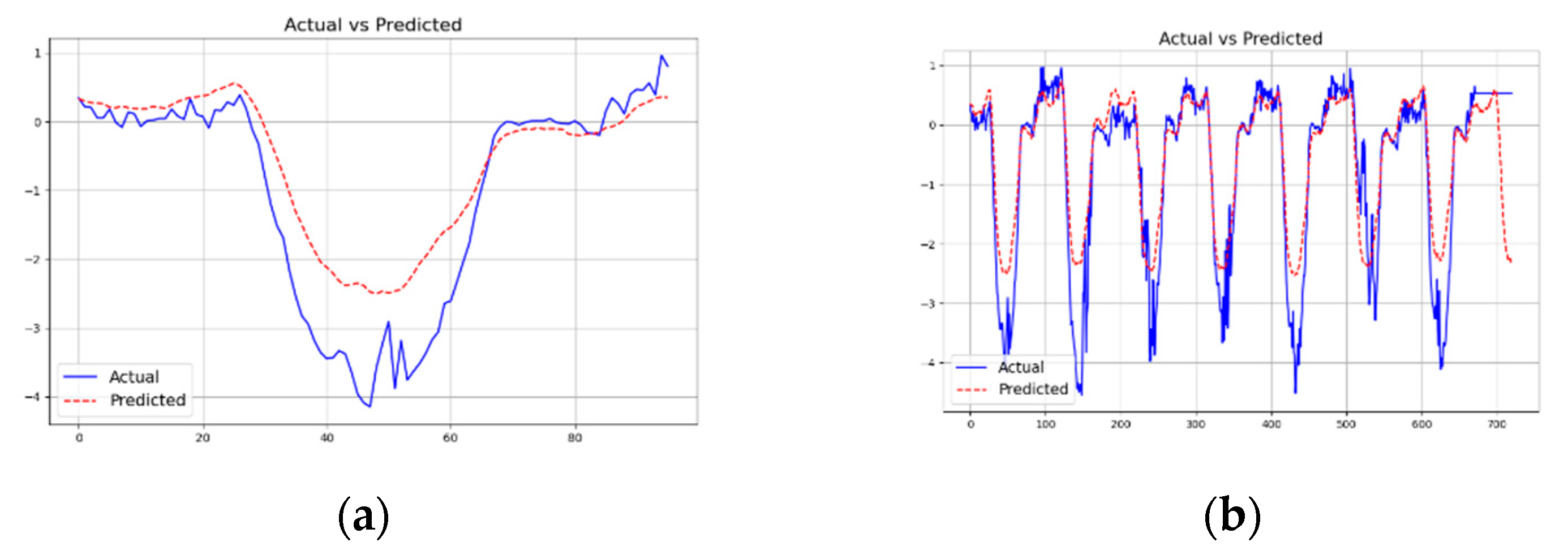
Table 1. Characteristics of the Different Datasets Used.

Table 2. Architecture Type of Different Models Used for Comparison.

Model	Type
FEDformer 1	Transformer-based
Autoformer	Transformer-based
Informer	Transformer-based
Pyraformer	Transformer-based
LogTrans	Transformer-based
DLinear	Non-Transformer
PatchTST	Transformer-based

Table 3. Comparison of Our ELM Model with Other Models on the Time Series Datasets.

Models		(our model) ELM		PatchTST/64		DLinear		FEDformer		Autoformer		Informer		Pyraformer
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
Weather	96	0.140	0.184	0.149	0.198	0.176	0.237	0.238	0.314	0.249	0.329	0.354	0.405	0.896	0.556
	192	0.183	0.226	0.194	0.241	0.22	0.282	0.275	0.329	0.325	0.37	0.419	0.434	0.622	0.624
	336	0.233	0.266	0.245	0.282	0.265	0.319	0.339	0.377	0.351	0.391	0.583	0.543	0.739	0.753
	720	0.306	0.319	0.314	0.334	0.323	0.362	0.389	0.409	0.415	0.426	0.916	0.705	1.004	0.934
Traffic	96	0.398	0.265	0.360	0.249	0.41	0.282	0.576	0.359	0.597	0.371	0.733	0.41	2.085	0.468
	192	0.408	0.269	0.379	0.256	0.423	0.287	0.61	0.38	0.607	0.382	0.777	0.435	0.867	0.467
	336	0.417	0.274	0.392	0.264	0.436	0.296	0.608	0.375	0.623	0.387	0.776	0.434	0.869	0.469
	720	0.456	0.299	0.432	0.286	0.466	0.315	0.621	0.375	0.639	0.395	0.827	0.466	0.881	0.473
Electricity	96	0.131	0.223	0.129	0.222	0.14	0.237	0.186	0.302	0.196	0.313	0.304	0.393	0.386	0.449
	192	0.146	0.236	0.147	0.240	0.153	0.249	0.197	0.311	0.211	0.324	0.327	0.417	0.386	0.443
	336	0.162	0.253	0.163	0.259	0.169	0.267	0.213	0.328	0.214	0.327	0.333	0.422	0.378	0.443
	720	0.200	0.287	0.197	0.29	0.203	0.301	0.233	0.344	0.236	0.342	0.351	0.427	0.376	0.445
Illness	24	1.820	0.809	1.319	0.754	2.215	1.081	2.624	1.095	2.906	1.182	4.657	1.449	1.42	2.012
	36	1.574	0.775	1.579	0.87	1.963	0.963	2.516	1.021	2.585	1.038	4.65	1.463	7.394	2.031
	48	1.564	0.793	1.553	0.815	2.13	1.024	2.505	1.041	3.024	1.145	5.004	1.542	7.551	2.057
	60	1.512	0.803	1.470	0.788	2.368	1.096	2.742	1.122	2.761	1.114	5.071	1.543	7.662	2.1
ETTh1	96	0.362	0.389	0.370	0.400	0.375	0.399	0.376	0.415	0.435	0.446	0.941	0.769	0.664	0.612
	192	0.398	0.412	0.413	0.429	0.405	0.416	0.423	0.446	0.456	0.457	1.007	0.786	0.79	0.681
	336	0.421	0.427	0.422	0.440	0.439	0.443	0.444	0.462	0.486	0.487	1.038	0.784	0.891	0.738
	720	0.437	0.453	0.447	0.468	0.472	0.490	0.469	0.492	0.515	0.517	1.144	0.857	0.963	0.782
ETTh2	96	0.263	0.331	0.274	0.337	0.289	0.353	0.332	0.374	0.332	0.368	1.549	0.952	0.645	0.597
	192	0.318	0.369	0.341	0.382	0.383	0.418	0.407	0.446	0.426	0.434	3.792	1.542	0.788	0.683
	336	0.348	0.399	0.329	0.384	0.448	0.465	0.4	0.447	0.477	0.479	4.215	1.642	0.907	0.747
	720	0.409	0.444	0.379	0.422	0.605	0.551	0.412	0.469	0.453	0.49	3.656	1.619	0.963	0.783
ETTm1	96	0.291	0.338	0.293	0.346	0.299	0.343	0.326	0.39	0.51	0.492	0.626	0.56	0.543	0.51
	192	0.332	0.361	0.333	0.370	0.335	0.365	0.365	0.415	0.514	0.495	0.725	0.619	0.557	0.537
	336	0.362	0.377	0.369	0.392	0.369	0.386	0.392	0.425	0.51	0.492	1.005	0.741	0.754	0.655
	720	0.418	0.409	0.416	0.420	0.425	0.421	0.446	0.458	0.527	0.493	1.133	0.845	0.908	0.724
ETTm2	96	0.160	0.246	0.166	0.256	0.167	0.260	0.18	0.271	0.205	0.293	0.355	0.462	0.435	0.507
	192	0.219	0.288	0.223	0.296	0.224	0.303	0.252	0.318	0.278	0.336	0.595	0.586	0.73	0.673
	336	0.271	0.321	0.274	0.329	0.281	0.342	0.324	0.364	0.343	0.379	1.27	0.871	1.201	0.845
	720	0.360	0.380	0.362	0.385	0.397	0.421	0.41	0.42	0.414	0.419	3.001	1.267	3.625	1.451
Exchange	96	0.084	0.201			0.081	0.203	0.148	0.278	0.197	0.323	0.847	0.752	0.376	1.105
	192	0.156	0.296			0.157	0.293	0.271	0.38	0.3	0.369	1.204	0.895	1.748	1.151
	336	0.266	0.403			0.305	0.414	0.46	0.5	0.509	0.524	1.672	1.036	1.874	1.172
	720	0.665	0.649			0.643	0.601	1.195	0.841	1.447	0.941	2.478	1.31	1.943	1.206

Table 4. Comparison of Our Swin transformer Model with Other Models on the Time Series Datasets. Results highlighted in bold signify the best performance, while those underlined indicate the second-highest achievement.

Models		(our) Swin Transformer		(our model) ELM		PatchTST/64		DLinear		FEDformer
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
Weather	96	0.173	0.224	0.140	0.184	0.149	0.198	0.176	0.237	0.238	0.314
	192	0.227	0.268	0.183	0.226	0.194	0.241	0.22	0.282	0.275	0.329
	336	0.277	0.305	0.233	0.266	0.245	0.282	0.265	0.319	0.339	0.377
	720	0.333	0.345	0.306	0.319	0.314	0.334	0.323	0.362	0.389	0.409
Traffic	96	0.621	0.342	0.398	0.265	0.360	0.249	0.41	0.282	0.576	0.359
	192	0.651	0.359	0.408	0.269	0.379	0.256	0.423	0.287	0.61	0.38
	336	0.648	0.353	0.417	0.274	0.392	0.264	0.436	0.296	0.608	0.375
	720	0.384	0.4509	0.456	0.299	0.432	0.286	0.466	0.315	0.621	0.375
Electricity	96	0.189	0.296	0.131	0.223	0.129	0.222	0.14	0.237	0.186	0.302
	192	0.191	0.296	0.146	0.236	0.147	0.240	0.153	0.249	0.197	0.311
	336	0.205	0.3107	0.162	0.253	0.163	0.259	0.169	0.267	0.213	0.328
	720	0.228	0.327	0.200	0.287	0.197	0.29	0.203	0.301	0.233	0.344
ILI	24	5.806	1,800	1.820	0.809	1.319	0.754	2.215	1.081	2.624	1.095
	36	6.931	1.968	1.574	0.775	1.579	0.87	1.963	0.963	2.516	1.021
	48	6.581	1.904	1.564	0.793	1.553	0.815	2.13	1.024	2.505	1.041
	60	6.901	1.968	1.512	0.803	1.470	0.788	2.368	1.096	2.742	1.122
ETTh1	96	0.592	0.488	0.362	0.389	0.370	0.400	0.375	0.399	0.376	0.415
	192	0.542	0.514	0.398	0.412	0.413	0.429	0.405	0.416	0.423	0.446
	336	0.537	0.518	0.421	0.427	0.422	0.440	0.439	0.443	0.444	0.462
	720	0.614	0.571	0.437	0.453	0.447	0.468	0.472	0.490	0.469	0.492
ETTh2	96	0.360	0.405	0.263	0.331	0.274	0.337	0.289	0.353	0.332	0.374
	192	0.386	0.426	0.318	0.369	0.341	0.382	0.383	0.418	0.407	0.446
	336	0.372	0.421	0.348	0.399	0.329	0.384	0.448	0.465	0.4	0.447
	720	0.424	0.454	0.409	0.444	0.379	0.422	0.605	0.551	0.412	0.469
ETTm1	96	0.400	0.421	0.291	0.338	0.293	0.346	0.299	0.343	0.326	0.39
	192	0.429	0.443	0.332	0.361	0.333	0.370	0.335	0.365	0.365	0.415
	336	0.439	0.447	0.362	0.377	0.369	0.392	0.369	0.386	0.392	0.425
	720	0.477	0.466	0.418	0.409	0.416	0.420	0.425	0.421	0.446	0.458
ETTm2	96	0.210	0.292	0.160	0.246	0.166	0.256	0.167	0.260	0.18	0.271
	192	0.264	0.325	0.219	0.288	0.223	0.296	0.224	0.303	0.252	0.318
	336	0.311	0.356	0.271	0.321	0.274	0.329	0.281	0.342	0.324	0.364
	720	0.408	0.412	0.360	0.380	0.362	0.385	0.397	0.421	0.41	0.42

Table 5. Comparison of our ELM model to Other Recently Published Models. Results highlighted in bold signify the best performance, while those underlined indicate the second-highest achievement.

Models	(our model) ELM		SpaceTime		DLinear		FEDformer		Autoformer		TimeMachine(Mamba)
Metric	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETTh1 720	0.448	0.463	0.499	0.48	0.440	0.453	0.506	0.507	0.514	0.512	0.462	0.475
ETTh2 720	0.387	0.428	0.402	0.434	0.394	0.436	0.463	0.474	0.515	0.511	0.412	0.441
ETTm1 720	0.415	0.409	0.408	0.415	0.433	0.422	0.543	0.49	0.671	0.561	0.430	0.429
ETTm2 720	0.348	0.377	0.358	0.378	0.368	0.384	0.421	0.415	0.433	0.432	0.380	0.396

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.