Preprint
Article
Optimal Investments in the Portfolia Yield Reactives (PYR)‡
Altmetrics
Downloads
106
Views
43
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
17 June 2024
Posted:
18 June 2024
You are already at the latest version
Alerts
Abstract
We evolve our past models PYR, Loukeris, et al. (2016) to provide a competitive system whose infiltration of categorical information and fundamentals into advanced higher moments, supports a more objective Portfolio Selection, aided by Intelligent Computing. The system of Portfolia Yield Reactives (PYR) searches for hidden prototypes into big data of accounting and financial statements, restricting malicious patterns such as hoax, noise, manipulation, incorporated to a novel optimal portfolio selection method.
Keywords:
Subject: Business, Economics and Management - Finance
I. Introduction
The Epicurus measure of Eudaimonia, (serenity), as a dominant characteristic in his philosophy of Hedonism influenced the mathematical thinking two Millennia later. Focusing on the attainment of pleasure that provides tranquility for each individual, should minimize the desires and banish the fear of gods and death. Epicurus agrees with Aristotle that happiness is the highest good, disagreeing to identify happiness with pleasure, because i) pleasure is the only thing that people do, thus Epicurean ethical hedonism is based on the psychological hedonism. ii) fits Epicurus’ empiricism, the introspective experience: pleasure is good and pain is bad. Epicurus claims that all our actions maximise the gain of pleasure for ourselves. Epicurus freedom was much later re-formalized in Economics as the diminishing marginal utility and the marginal propensity to consume. The quadratic investor preferences and the returns distributions of Normal probability as given by the von Neumann-Morgenstern axioms of choice is the main approach in many portfolio selection models that follow Markowitz’s mean-variance criterion. The empirical practice and the academic research clarified that neither of the two conditions hold, as non-quadratic distributions, are more efficient for describing investment patterns, and the returns are non-Normally Independently and Identically Distributed, Merton, (2009). The Power Utility Function demonstrated a slight superior performance towards the Quadratic function, (Loukeris et al., 2013, 2014b). Further extending the use of higher moments than the fourth, establishes new qualities in the utility function behavior. Investors usually select positive skewness, derived of high profits from extreme positive events, Boyle and Ding (2005). Also prefer low kurtosis of low risk caused by extreme losses or profits in both sides of the distribution, (Athayde and Flores, 2003), (Ranaldo and Favre, 2003), (Lai, Yu and Wang, 2006). (Loukeris et al., 2013, 2014b, 2021), and (Loukeris, 2021), (Loukeris et al., ,2021) remarked that advanced modeling is necessary to provide upgraded reliability to investors’ preferences under advanced higher moments. The m10 HyperUltraKurtosis, in the Expected Utility, reflects more detailed forms of risk, eliminating hoax, noise, or manipulation effects. The risk is not fully expressed in the m2 (σ), whilst the m4 (Kurt) includes valuable information on fat tails and leptokurtosis, thus even higher moments add information. The Hypothesis we make at this point is that the noise of systemic risk is provided by biased expectations or manipulation. We have had many cases that support this phenomenon: the Madoff pyramids (Markopolos 2010), the Toxic Bonds, (Antonakakis and Vergos, 2013), the Greek Crisis (Fasianos and Tsoukalis, 2023), and many other cases of varying magnitude, that produce bubbles and instabilities.
Subrahmanyam (2007) rejects the theories of rational utility maximizers as an optimal behavioral tool as they are non-realistic, far from the markets. Thus, we provide a more analytical tool that incorporates critical and hidden information to optimize portfolio and to conclude on the best selection, avoiding imperfect evaluations of the data and assets. The PYR model is the integrated solution on this complicated fractal domain of advanced entropy that requires robust classifiers to support it. It is specialized in:
- [1]
- Incorporating advanced moments, up to the ninth of hyperskewness and the tenth of hyperultracurtosis as the tools to extract behavioral patterns of investors and offering them a customized solution of optimal portfolio
- [2]
- extracting hidden accounting and sentiments data through the fusion of fundamentals and price data
- [3]
- concluding on the best classifier among SVM, RBF and GFF networks to support the complex solution process with Computational Intelligence
- [4]
- demonstrating the novel Portfolio Yield Reactive Model – PYR
- [5]
- removing inferior assets from the solution space (less efficient)
Based on the Markowitz (1952) Portfolio Theory, we propose a more analytical system of integrated portfolio optimisation. After calculating the investors profile in detail, we process the desired assets through the PYR model, the solution space is created, and the best portfolio is selected. The PYR model requires robust classifiers that are determined out of the three families of AI models that are examined here in neural and hybrid neuro-genetic form. High level portfolio optimization methods are used to select the perfect companies that are the best for the particular investor’s portfolio.
The rest of this paper is organized as follows. Section 2 describes the Behavioral theoretical part Section 3 analyses the Higher moments in our model of portfolio selection with the Isoelastic Utility, the innovative limits of fundamentals in Intelligent Computing. Section 4 demonstrated the Methodology. Section 5 the Data. Section 6 supports the discussion of the Results and Section 7 provides the Conclusions.
II. Behavioral Parameters
In actual markets a high level of bias is endogenous on the portfolio, with limited diversification, Fidora, (Fratzscher and Thimann 2006), (Coeurdacier and Rey 2012). The risk differentials on stocks cause a partial effect in the cross-section of expected returns, (Ang, Hodrick Xing, and Zhang 2006), whilst data-mining is a significant aspect of empirical work. The risk effect is nonlinear on returns and needs more analytical tools such as those we develop in this research. This loss avoidance agrees with the Epicouros (306 BC) philosophy of Hδονισμός (Hedonism-pursuit of pleasure), where the main goal of individuals is Hδονή – pleasure, through Aπονία – avoidance of unnecessary pain (risk). The loss-averse investors with lesser emphasis on risk averse is the core of our model, because the emphasis is given on the preservation of current profits and wealth, rejecting extra risk that expose to losses. The non-rational patterns of firm’s proximity to investor, time, period of the year, gender, etc also have an impact on uncertainty and thus complexity.
III. The Free Will Problem under Higher Moments
The returns are non n.i.i.d. as the Efficient Market Hypothesis is insufficient to describe the complex real market phenomena. Subrahmanyam (2007), underlined that investors are interested mainly in their potential losses. The analytical matching of behavioral hedonism to detailed forms of higher moments returns, and pain to detailed forms of loss is significant for a balanced model that optimizes the portfolio to the investors. The investors optimize their utilitarian preferences balancing fears and expectations to their earnings. Loukeris et al. (2014b, 2016), (Loukeris et al. 2021), (Loukeris, 2021) introduced the 5th moment of hyperskewness, the 6th of hyperkyrtosis, the 7th ultraskewness and 8th ultrakurtosis as detailed measures of gain and pain.
The principal problem of Philosophy and Medicine on the free will is tantalizing science since the beginning of civilization. Ordinal perception supposes that we are in full responsibility of our choices, but the limits of freedom and will are complex. On one hand it is believed that the freedom to select and act is produced by the freedom of will. On the other hand, it is believed that our will cannot be managed by us. The Incompatibilists support that determinism is irreconcilable with freedom, although the incompatibilist freedom puts emphasis on randomness replacing determinism. The Compatibilists support that determinism and freedom are consistent. Whilst the Libertarians declare the existence of freedom, on the contrary Sceptics believe that freedom is impossible, (Pink, 2004). Libertarian free will does not exist, (Johnson, 2016). The free will concept, concludes on the impossibility for our free will judgements— on the freedom of our actions—to be systematically false (Latham, 2019). Although (Colsane and Riccetti, 2021) noted that the research stops ordinarily to the fourth moment, because behaviors at higher orders are often the same of making random choices, but they neglect that the patterns of subconscious that are reflected to ego and alter logical thinking should be taken into consideration. Also the unconscious that produces random forms of thinking is reflected hierarchically to the previous levels, so nature follows a random pattern in its essence. Thus, higher order moments reflect these detailed forms of behavior in gain and loss that have non-linear form, to the limits of randomness.
In this paper, we introduce the 9th of hyperultraskewness, and the 10th of the hyperultrakurtosis on the Isoelastic Utility Function. The HARA - Hyperbolic Absolute Risk Aversion family incorporates the Isoelastic as well as the group of utility functions of Constant Relative Risk Aversion, the CRRA, thus our approach can be written as:
where
Where Ut(Rt+1) is the overall utility the investor receives, a proportion of mean return in the overall happiness of the investor, Et(Rt+1) is the expected return, a the proportion of return, b the proportion of risk to the utility measure, Vart(Rt+1) is the variance, c the proportion of skewness in the investor’s happiness, Skewt(Rt+1) the skewness, d the proportion of Kurtosis, Kurtt(Rt+1) the kurtosis of the investment, e the proportion of HyperSkewness, HypSkewt(Rt+1) the HyperSkewness, f the proportion of HyperKurtosis, HypKurtt(Rt+1) the HyperKurtosis of the investment, etc.(2, 3, 4) as a series of higher order moments can be extended to the desired level of analysis. The general form, Loukeris et al. (2016) of the utility function is:
where λν is the accuracy of investors utility preferences to risk, depending on the behavior, aλν a constant on investors’ profile: aλν = 1 for rational risk-averse individuals, aλν ≠ 1 for the non-rational, ri the value of return i in time t, μ the Expected return, n the number of assets in the portfolio, ω the amount of observations on the accuracy of investors utility preferences, according to the examined set. The Isoelastic Utility, of Constant Relative Risk Aversion, is on the risk-averse investors:
where λ a measure of risk aversion, W the wealth.
Ut(Rt+1) = aEt(Rt+1) – bVart(Rt+1) + cSkewt(Rt+1) - dKurtt(Rt+1) + eHypSkewt(Rt+1) – fHypKurtt(Rt+1) + gUltraSkewt(Rt+1) –hUltraKurtt(Rt+1) + iHypUltraSkewt(Rt+1) –kHypUltraKurtt(Rt+1)
Kurtt(Rt+1) = Vart2(Rt+1)
HypKurtt(Rt+1) = Vart(Rt+1) Kurtt(Rt+1) = Vart3(Rt+1)
HypUltraKurtt(Rt+1) = Kurtt2(Rt+1) = Vart4(Rt+1)
(Loukeris et al. 2014b, 2016), (Loukeris,. 2021), (Loukeris et al. 2021), revealed that the Makowitz model can ease its essential assumption on the normally distributed prices.
IV. Methodology
A. Past models
The convex problem of quadratic utility maximization, Markowitz (1952), is a vague approach on the markets. Maringer and Parpas (2009) reformed it to:
where rp portfolio’s p return, Var (r) the variance-risk, E(r) the expected return, λ their proportion.
B. Problem Definition
Loukeris et al. (2014b, 2016), and (Loukeris et al. 2016), noticed the necessity of advanced higher preferences to :
where rp portfolio’s p return, Var(r) the variance, Kurt(r) the Kurtosis, HypKyrt(r) the Hyper-Kurtosis, HypUltra Kurt(r) the Hyper-Ultra-Kurtosis, λ their proportion.
where ri* stock’s i return on the efficient frontier, υγ the company’s financial health (binary: 0 to bankruptcy, 1 healthy), ετ the heuristic model output that is the evaluation result (binary: 0 healthy, 1distressed), xi their weights.
minxf(x)=λυγ[bVart(rp)+dKurtt(rp)+fHypKurtt(rp)+hUltraKurtt
(rp)+kHypUltraKurtt(rp)]
The superiority of the selected stocks in the portfolio is:
i* sup j if and only if Rt(i*)>Rt(j), in:
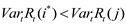
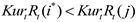

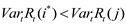
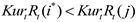

UltraKurtRt(i*) < UltraKurtRt(j)
HypUltraKurtRt(i*) < HypUltraKurtRt(j)
Although high order moments may not be estimated reliably, the use of historical big-data create the behavioural profile of investors. Higher order moments in terms of risk eg. Hyperkurtosis, Ultrakurtosis, Hyperultrakurtosis remark the detailed relative importance of tails as compared to shoulders in contribution to kurtosis, to hyperkurtosis and ultrakurtosis respectively. Thus, the propensity of higher degrees of freedom on risk can be calculated, and depict multidimensionally the risk preferences to the investor. Put simply the sensitivity of risk on the selected portfolio. Similar is the effect of return and its higher moments.
The hoax exposure would have been filtered earlier in the fundamentals and returns fused new Utility function.
Stocks that do not support all these superiority conditions are non-optimal, below the efficient frontier, and removed from the optimal portfolio set. Hence the Utility becomes, (Loukeris et al., 2014b, 2016), (Loukeris et al. 2021):
in
Being identical to
As
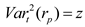 then
then
for 

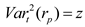
as 

minxf(x) = λυγ Vart(rp)[b+dy+fz +hzy+kz4]
This non-convex problem, requires robust heuristics. Our novel contribution is that we extract hidden accounting and financial prototypes to a more detailed stock’s evaluation. The undetected trends in the asset can provide valuable information to investors. Hoax and manipulation is an important risk to investors. Hidden patterns include cooked accounting, corporate fraud, stock manipulation, hoaxes, undetected critical accounting/financial data. (9) and (22) filter the distressed companies with no significant potential from portfolios. The evaluation υγ, in (9) is more important than the investor’s risk behavior, as they have a reverse influence in υγ/λ. The minx f(x) in (8, 23) remarks a categorical, objective influence of a stock than subjective investors’ behavior. It provides measurable pricing than non-rational expectations and biases. The performance of portfolios is by their risk and return’s detailed performance, but this will be analysed in future papers. The flow chart of processes is in Figure 1.
V. The Portfolio Yield Reactives (Pyr)
The Portfolia Yield Reactives model (PYR) is an advanced form of the integrated PI - Portfolio Intelligence model, Loukeris et al. (2016).
In the first step read the fundamentals, the accounting data, the market prices, and the preferred optimization period t.
Then it proceeds by selecting the initial method to evaluate the companies whose stocks are candidates in the portfolio. On this step the individual investor’s risk profile is given and the λ is selected for the Isoelastic utility, or it is re-calculated depending on the new market data.
If the optimal portfolio is in risk level λ then withhold, end.
Else Calculate new λ, and read new λ.
If the new data on the selected stocks, or rest of the market stocks, and assets are different and include additional value,
Then there is Local Optimal Portfolio.
If the profit of the Local Optimal Portfolio on the current investment time horizon is acceptable
Then withhold, end.
Else re calculate portfolio.
In the next step, the system examines if this is the last firm to be examined and if the condition for the optimal portfolio as an efficient portfolio is satisfied.
Else we proceed to the next of the initial evaluation that uses a Computational Intelligence model, to create two subsets: Subset A of the healthy companies, and Subset B of the distressed firms.
In the specific model we select the best network among the RBFs, the SVMs and the MLP, that is the hybrid SVM of 500 epochs optimized by GAs on the inputs only and Cross Validation, The ετ value is calculated (0, for the healthy and 1 for the distressed firms).
If ετ = 1 then the firm is distressed and it is removed, else if ετ = 0 the firm is healthy being candidate for the optimal efficient portfolio.
On the next step the Ut(Rt(i)) the utility function of (14) is calculated per firm.
Next, firms are ranked according to their utility score.
Then, the Efficient Frontier is calculated.
Next, the firms with the higher utility score are selected into the efficient portfolio.
The sub-optimal firms as well as the non-optimal firms are revaluated with potential new data on step 4 of Neural Nets evaluation, following all the steps.
Next, after the efficient portfolio is created, its Utility Function is calculated UPj(f).
Then, the optimal overall portfolio U*Pj(f) whose utility is the maximum available, is detected, if possible, by all the available efficient portfolio utilities UPj(f) recorded in U*Pj(f)> UPj(f).
The process stops when the time limit is reached and the PYR has the optimal portfolio.
The key idea is to filter fraud and speculative noise that interfere on the price and disorient investors. Thus, examining recent accounting entries and financial indexes we conclude on the realistic financial health of the
firm. Then the actual healthy firms are selected, proceeding to the detection of efficient frontier and the creation of the optimal portfolio.
The Portfolio Yield Reactive (PYR) model seeks to build a robust icon on the investor behavior based on big-data, thus it can reflect the wealth preferences more analytically. Additionally, the introduction of fundamentals as another process can support the filtration of bias in the form of manipulation, hoaxes or other non-ethical actions. Thus, PYR is a novel tool for portfolio optimization with cutting-edge AI classifiers.
VI. The Processing Phase
VII. The Support Vector Machines
The Support Vector Machines-SVM, (Figure 2) produce general regression, and classification functions from a
set of labeled training data, Cortes and Vapnik (1995), on a binary output, as input is categorical. Courtis (1978), noted that for instances xi, i = 1,…l in labels yi {1,−1}, SVM is trained optimising:
under: 0 ≤ αi ≤ C, i= 1,…l, yT α = 0,
where, e the vector of all 1, Q an lXl symmetric matrix of
Qi,j= yi yj K(xi, xj)
K(xi, xj) the kernel function, and C the upper bound of all variables. Unstable patterns are rejected by the SVM,
as overfitted, receiving a statistically acceptable solution. These SVMs use the Adatron kernel algorithm, Friess, Cristianini, and Campbell, (1998), mapping inputs to a high-dimensional feature space, separating data into their respective classes and isolating the inputs which fall close to the data boundaries. The converging system produces a few αi ≠0, the support vectors, interacting with the closest boundary samples among classes. The Adatron kernel adjusts the RBFN in an optimal margin and prunes the RBF net so that its output for testing is for i support vectors:
where G(x, σ2) a Gaussian function, gi and αi a set of multipliers each to a sample, and the input space is augmented by one dimension with a constant value of 1 to provide the bias β.
VIII. The Hybrids Support Vector Machines
All the classifiers, including the SVMs were evaluated in Hybrid neural-genetic modes (Figure 3). The inputs were 16 financial indices and the desired evaluation by executives. None of the 16 inputs has a predefined significance to the hybrid genetic SVMs. The GAs selects important inputs, demanding a multiple training of the network to define the minimum error. In accordance to Min, Lee, and Han, (2006), where optimisation emphasises on the feature subset and the SVM parameters, we move forth examining multiple hybrid SVM models. Specifically, the GAs were elaborated in different hybrids: i) the SVM inputs only, ii) the SVM outputs only, and iii) both the inputs and outputs. Batch learning was preferred on the weights after the presentation of the whole training set. All models were tested on 500 and 1000 epochs respectively, to optimize the iterations number upon convergence. Min, Lee, and Han, (2006), performed the feature selection either on the filter, or the wrapper approach. The filter approach is computationally more efficient, but the wrapper approach, although slower, selects the features more optimally. In the bankruptcy prediction problem, feature subset selection plays an important role in the performance of prediction. Furthermore, its importance increases when the number of features is large.
This paper uses the wrapper approach to select the SVM optimal training. The increase function is selected to terminate training under the Cross Validation set when its MSE increases, avoiding the overtraining, whilst the best training weights are loaded on the test set. The GA solved the optimal values problem in a) number of neurons, b) the Step size, and c) the Momentum Rate, requiring a multiple training of the network to conclude the lowest error mode. In the case of the models with GA on the output layer, they optimized the value of the Step size and the Momentum. The higher number of epochs allowed iterations to provide thorough analysis of the network, the overall classification of these SVM models was excellent taking as a benchmark the bank experts’ initial opinion, with a fine performance in almost all the model parameters, that failed to reduce overtraining hazard in almost all different SVM hybrid or SVM models, questioning the model’s independence, and impartiality.
IX. The Generalised Feedforward Neural Networks
The Generalized feedforward networks (GFF), (Figure 4) extended the Shunting Inhibitory Artificial Neural Network (SIANNs) Bouzerdoum (1999, 2000), consisting a generalization of the MLP such that connections can jump over one or more layers. Although theoretically an MLP can solve any problem undergone by the GFFs, however, the GFFs often solve the problem much more efficiently. A typical MLP requires hundreds of times more training epochs than the generalized feedforward network containing the same number of neurons.
X. The Generalized Feedforward and Hybrid Networks
The Hybrid form of the GFFs (Figure 5), can have Genetic Algorithms, Holland (1992), optimization in various layers, that advance the processing of certain parameters on the core of the neural GFF. On the GFFs the GA optimization took place in different hybrids:
- a)
- the GFF with GAs on inputs only,
- b)
- the GFF with GAs on inputs and outputs only, and
- c)
- the GFFs with with GAs on both the inputs and outputs.
XI. The Radical Basis Functions Neural Networks
The Radial basis Function Neural Networks-RBFs (Figure 6), are linear models of regressions, classifications and time series predictions in supervised learning, consisting a universal approximator, Broomhead and Lowe (1988), as its interpolation and generalization properties are thoroughly investigated. The set of examples contains the independent variable, sensitive to noise, and the dependent one.
XII. The Radical Basis Functions Hybrids
The importance of each financial index out of the 16 inputs in the RBF hybrid nets (Figure 7), is unknown to the model and Genetic Algorithms investigate them. Each model is trained multiple times to define the input combination of the lowest error. Genetic Algorithms were implemented in different RBF hybrid models:
- a)
- on the inputs layer only,
- b)
- on the inputs and outputs layers only,
- c)
- in all the layers and cluster centers,
- d)
- in all the layers and cluster centers with cross-validation,
in different topologies. Batch learning was also selected to update the weights of the hybrid neuro-genetic RBFs, after the entire training set is presented. The competitive rule was the ConscienceFull function in Euclidean metric as the conscience mechanism keeps count on how often a neuron wins the competition, and
enforces a constant wining rate across the neuron s. There were 4 neuron s per hidden layer, using the TanhAxon transfer function, on the Momentum learning rule. Genetic Algorithms resolved the problem of optimal values in a) neurons, b) step size, c) momentum rate, and d) cluster centers.
RBF nets require multiple training to obtain the lowest error. The output layer elaborated Genetic Algorithms in some hybrids optimizing the Step size and the Momentum.
XIII. Data
Data were produced by 1411 companies from the loan department of a Greek commercial bank, with the following 16 financial indices:
1) EBIT/Total Assets,
2) Net Income/Net Worth,
3) Sales/Total Assets,
4) Gross Profit/Total Assets,
5) Net Income/Working Capital,
6)Net Worth/Total Liabilities
7)Total Liabilities/Total assets,
8) Long Term Liabilities/(Long Term Liabilities + Net Worth),
9)Quick Assets/Current Liabilities
10)(Quick Assets-Inventories)/Current Liabilities,
11)Floating Assets/Current Liabilities,
12)Current Liabilities/Net Worth,
13) Cash Flow/Total Assets,
14)Total Liabilities/Working Capital,
15)Working Capital/Total Assets,
16) Inventories/Quick Assets,
and a 17th index with initial classification, done by bank executives. The test set was 50% of the overall data, and the training set was 50%. Multiple combinations were chosen to detect the performance of SVM and RBF Networks:
- SVM of 500 or 1000
- SVM of 500 epochs and GA on inputs
- SVM of 1000 epochs and GA on inputs
- SVM of 500 epochs and GA on outputs
- SVM of 1000 epochs and GA on outputs
- SVM of 500 epochs and GA in all layers
- SVM of 1000 epochs and GA in all layers
- SVM of 500 epochs and GA on inputs, and Cross-Validation
- SVM of 1000 epochs and GA on input, and Cross-Validation
- GFF Neural Nets,
- GFF hybrids in inputs GA,
- GFF hybrids in inputs and outputs GA,
- GFF hybrids of GA in all layers,
- GFF hybrids of GA in all layers and Cross Validation,
- RBF Neural Nets,
- RBF hybrids in inputs GA,
- RBF hybrids in inputs and outputs GA,
- RBF hybrids of GA in all layers,
- RBF hybrids of GA in all layers and Cross Validation,
XIV. Results
A comparison of all the outcomes would rank first among all the SVM, RBF, GFF and MLP models the hybrid
GFF in GAs over the input and output layer only, of 1 layer, 98.9% correct classifications for the healthy and 88.52% the distressed firms, a fine fitness to the data at 0.908, the lowest Akaike at -1907.09 in the best impartiality, low errors at MSE 0.072, NMSE 0.170, and 5.77% in a fast processing of 55 minutes 18 seconds.
All the other models despite of their superior classification and performance they demonstrated very high values of partiality and thus are exposed to overfitting, being lower reliability classifiers for this numerical financial problem.
The second rank is given to the SVM of 500 epochs optimized by GAs on the inputs only and Cross Validation, in a 100% classification of the correct classified assets, a fitness of the model to the data r 0.999 of the lowest error in MSE at 0.023, NMSE 0.045, overall error 4.01% but a significant partiality of Akaike 12044.20, extended training time of 26 hours 56 minutes 14 seconds. Time is not an issue for the trained model, as the cross-validation reduces overfitting. The main vulnerability of partiality shows dependence of its performance by the Desired Classification as given by human experts. But this is of lower significance as the CV set was quite good, with 94.29% correct classifications on the healthy companies, 77.98% on the distressed in a medium error of 0.309 in MSE, 0.591 on NMSE, 12.72% on overall error.
The third rank was taken by the SVM of 500 epochs in excellent classification, performance and a very fast time, exposed to overfitting and partiality.
Fourth was ranked the SVM of 100 epochs in excellent outcomes of classification, performance, and time, in the same weaknesses of overfitting and partiality.
The RBFs underperformed in classification, but with a very high fitness 0.925, in high error and AIC as well. The other RBF models and the MLP significantly underperformed and ranked last than the SVMs (Tables I, Tables II and Tables III). The integrated PYR model thus will have robust classifiers depending the need of the users, the depth of accuracy, the form of the data. As an overall portfolio selection system, it eliminates market manipulation incorporating the fundamentals as comparative parameters to the stock return in the markets, and also introduces more processes of re-evaluation for the optimization of the investment portfolio.
XV. Conclusions
The integrated model Portfolia Yield Reactives - PYR, offers an advanced analytical processing in the Decentralised Finance – De.Fi., supporting the real time portfolio selection problem. The main advantage of this system is that by extracting hidden patterns it tries to avoid manipulation, and speculation games. Although the hybrid SVMs nets have a promising performance of high calibration, their high overfitting abilities make them inappropriate classifiers. Thus, an optimal classification choice will be the GFF of 1 layer with GA oprimisation in the inputs and outputs only with a fine classification, low error and the lowest Akaike, in a computational time of 55 minutes, that can allow them to be a part of this model or its future upgrades, (Table IV). The hybrid SVM of 500 epochs optimized by GAs on the inputs only and Cross Validation although it provides a perfect performance and classification, in a restricted processing time, demonstrates a significantly higher partiality, as the SVM of 500 epochs despite its slight underperformance demonstrates robust qualities that suffer from overfitting and partiality (Table IV). Hence the SVM models despite their perfect classification, on condition for financial data, the RBF that had a quite lower performance with much more weaknesses or even worse some of the GFFs are inferior classifiers. The current research indicated a novel approach on the portfolio optimization problem. The black-box effect however is the usual problem with neural nets and sets limits to the repetition of their superiority. Future work will examine in detail the numerical results of utilities and wealth impact of the current models incorporating the new trends in the bubbles effects.
Funding
Please add: “This research received external funding by the ELKE Fund of the Universities of Macedonia and West Attica”
Conflicts of Interest
“The authors declare no conflict of interest.”
References
- Ang A., Hodrick R., Xing Y., and X., Zhang (2006), The Cross-Section of Volatility and Expected Returns, Journal of Finance, Volume LXI, No1, February. [CrossRef]
- Antonakakis N., and K., Vergos, (2013), Sovereign bond yield spillovers in the Euro zone during the financial and debt crisis, Journal of International Financial Markets, Institutions and Money, Volume 26, Pages 258-272, ISSN 1042-4431. [CrossRef]
- Athayde, G., and R. Flores, (2003), Incorporating skewness and Kurtosis in portfolio optimization: a multidimensional efficient set. In: Satchell, S., Scowcroft, A. (eds.) Advances in Portfolio Construction and Implementation, pp. 243–257. Butterworth-Heinemann, Oxford.
- Bouzerdoum A., (1999), A new class of high-order neural networks with nonlinear decision boundaries, Proceedings of the Sixth International Conference on Neural Information Processing (ICONIP ‘99), Perth, Australia, pp. 1004-1009.
- Bouzerdoum A., (2000), Classification and function approximation using feed-forward shunting inhibitory artificial neural networks, Proceedings of the International Joint Conference on Neural Networks (IJCNN 2000), Como, Italy, pp. 613-618.
- Broomhead S., and D. Lowe, (1988), Multivariable functional interpolation and adaptive networks, Complex Syst., 2, pp. 321-355.
- Coeurdacier N., and H., Rey (2012), Home Bias in Open Economy Financial Macroeconomics, Journal of Economic Literature, 51(1), 63-115, . [CrossRef]
- Colasante, A., and L., Riccetti, (2021), Financial and non-financial risk attitudes: what does it matter? Journal of Behavioral and Experimental Finance, 30, 100494). [CrossRef]
- Cortes C. and Vapnik V. (1995), Support-vector network, Machine Learning, 20:273–297. [CrossRef]
- Courtis, J. K., (1978), Modeling a Financial Ratios Categoric Framework, Journal of Business Finance & Accounting., 5(4): 371-386. [CrossRef]
- Fasianos A., and P., Tsoukalis, (2023), Decomposing wealth inequalities in the wake of the Greek debt crisis, The Journal of Economic Asymmetries, Volume 28, e00307, ISSN 1703-4949. [CrossRef]
- Fidora M., Fratzscher M., and C., Thimann (2006), Home Bias in Global Bond and Equity Markets – The role of real Exchange Rate Volatility, European Central Bank, Working Paper Series 685, October. [CrossRef]
- Friess, T., Cristianini, N., and ICG., Campbell, (1998). The Kernel-Adatron Algorithm: A Fast and Simple Learning Procedure for Support Vector Machines. In J. W. Shavlik (Ed.), ICML ‘98 Proceedings of the Fifteenth International Conference on Machine Learning (pp. 188 - 196). Association for Computing Machinery (ACM). https://dl.acm.org/citation.cfm?id=657470.
- Johnson, D. K., (2015), Does Free Will Exist? Think , Volume 15 , Issue 42, Spring 2016 , pp. 53 - 70.
- Holland, J., (1992), Adaptation in Natural and Artificial System, Cambridge, MA: MIT Press. ISBN 978-0262581110.
- Lai, K.K., Yu, L., and S. Wang, (2006), Mean-variance-skewness-kurtosis-based portfolio optimization, First International Multi-Symposiums on Computer and Computational Sciences (IMSCCS’06) Volume 2, 292–297. [CrossRef]
- Latham, A. J., (2019), The Conceptual Impossibility of Free Will Error Theory, European Journal of Analytic Philosophy, Volume 15 No. 2, . [CrossRef]
- Loukeris N., and I.Eleftheriadis, (2013), A novel Approach on Hybrid Support Vector Machines into Optimal Portfolio Selection, Proceedings of the IEEE International Symposium on Signal Processing and Information Technology, December 12-15, Athens, Greece. [CrossRef]
- Loukeris N., Eleftheriadis I. and E. Livanis (2014), Portfolio Selection into Radial Basis Functions Networks and neuro-genetic RBFN Hybrids, IEEE 5th International Conference on Information, Intelligence, Systems and Applications IISA, July 7-9, Chania Greece,. [CrossRef]
- Loukeris N., Bekiros S., and Eleftheriadis I., (2016), The Portfolio Yield Reactive (PYR) model, IEEE 6th International Conference on Information, Intelligence, Systems and Applications, IISA2016, 13-15 July, Porto Carras Grand Resort Hotel, Halkidiki, Greece,. [CrossRef]
- Loukeris N., (2021), The Evolutional Returns Optimisation System – EROS, IEEE 2021 International Conference on Data Analytics for Business and Industry (ICDABI), 25-26 October, Sakheer, Bahrain. [CrossRef]
- Loukeris N., Eleftheriadis I., (2021), Selecting Optimal Portfolio in Generalised Feed Forward networks and Self Organized Features Maps hybrids, IEEE 2021 International Conference on Computational Science and Computational Intelligence, CSCI 2021, Symposium on Artificial Intelligence (CSCI-ISAI) 15-17, December, Las Vegas, Nevada, USA.
- Maringer D., and P. Parpas, (2009), Global Optimization of Higher Order Moments in Portfolio Selection, Journal of Global Optimization. Volume 43, Numbers 2-3, March, . [CrossRef]
- Markopolos, H., (2010), No One Would Listen: A True Financial Thriller, John Wiley & Sons ISBN 978-0-470-55373 -2.
- Markowitz, H.M., (1952), Portfolio selection, Journal of Finance 7(1), 77–91. [CrossRef]
- Merton, R.C., (2009), Continuous-time finance, revised edition, 1992 ed. Blackwell,.
- Min S. H., Lee, J., and I. Han, (2006), Hybrid genetic algorithms and support vector machines for bankruptcy prediction, Expert Systems with Applications, 31(3), October, pp 652-660. [CrossRef]
- Pink T., (2004), Free Will: A Very Short Introduction, Oxford University Press.
- Ranaldo, A., and L. Favre, (2003), How to price hedge funds: from two- to four-moment CAPM, Technical report, EDHEC Risk and Asset Management Research Centre.
- Subrahmanyam, A., (2007), Behavioral Finance: A Review and Synthesis, European Financial Management, Volume 14, pp. 12–29. [CrossRef]
Figure 1.
The proposed model .
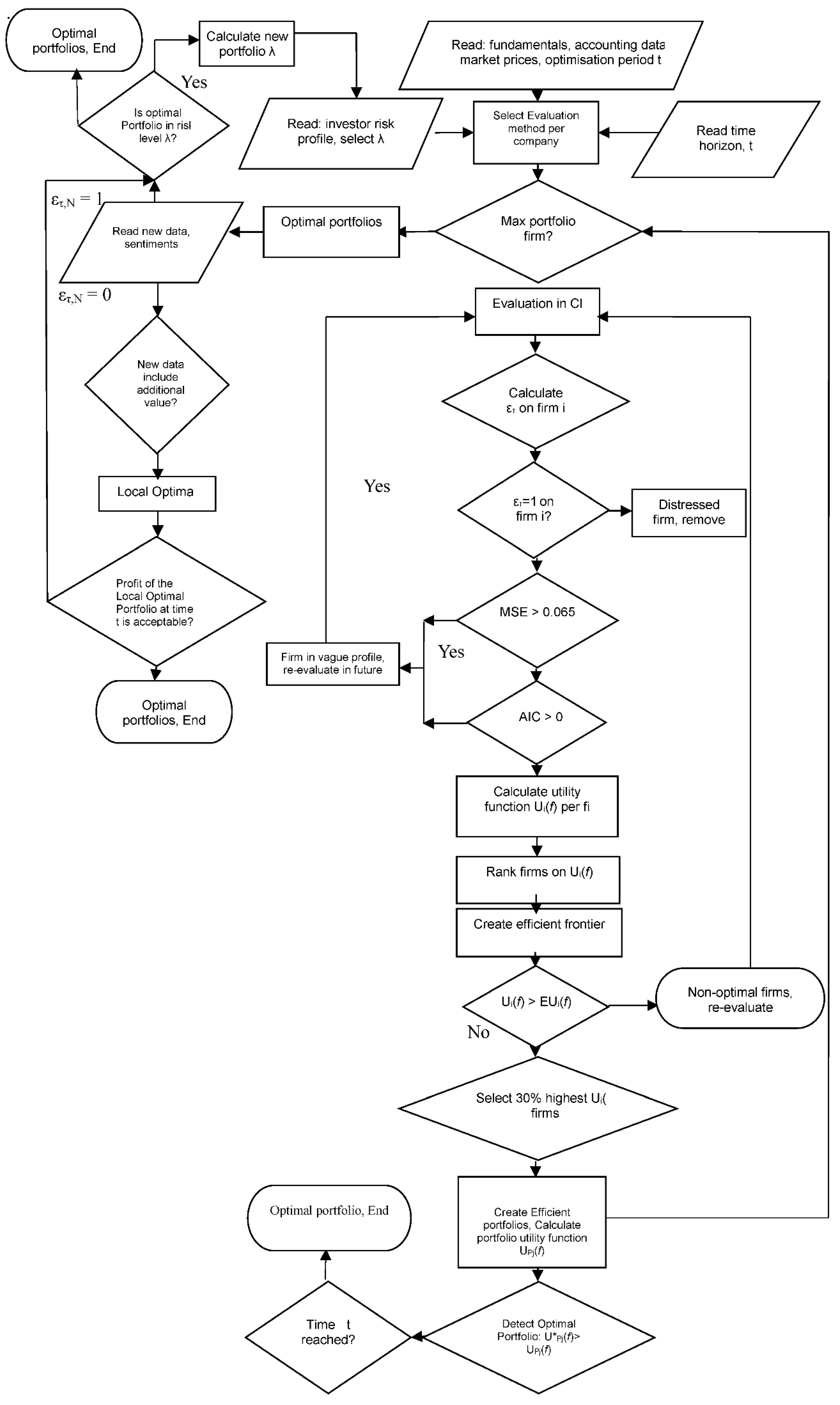
Figure 2.
Support Vector Machines.
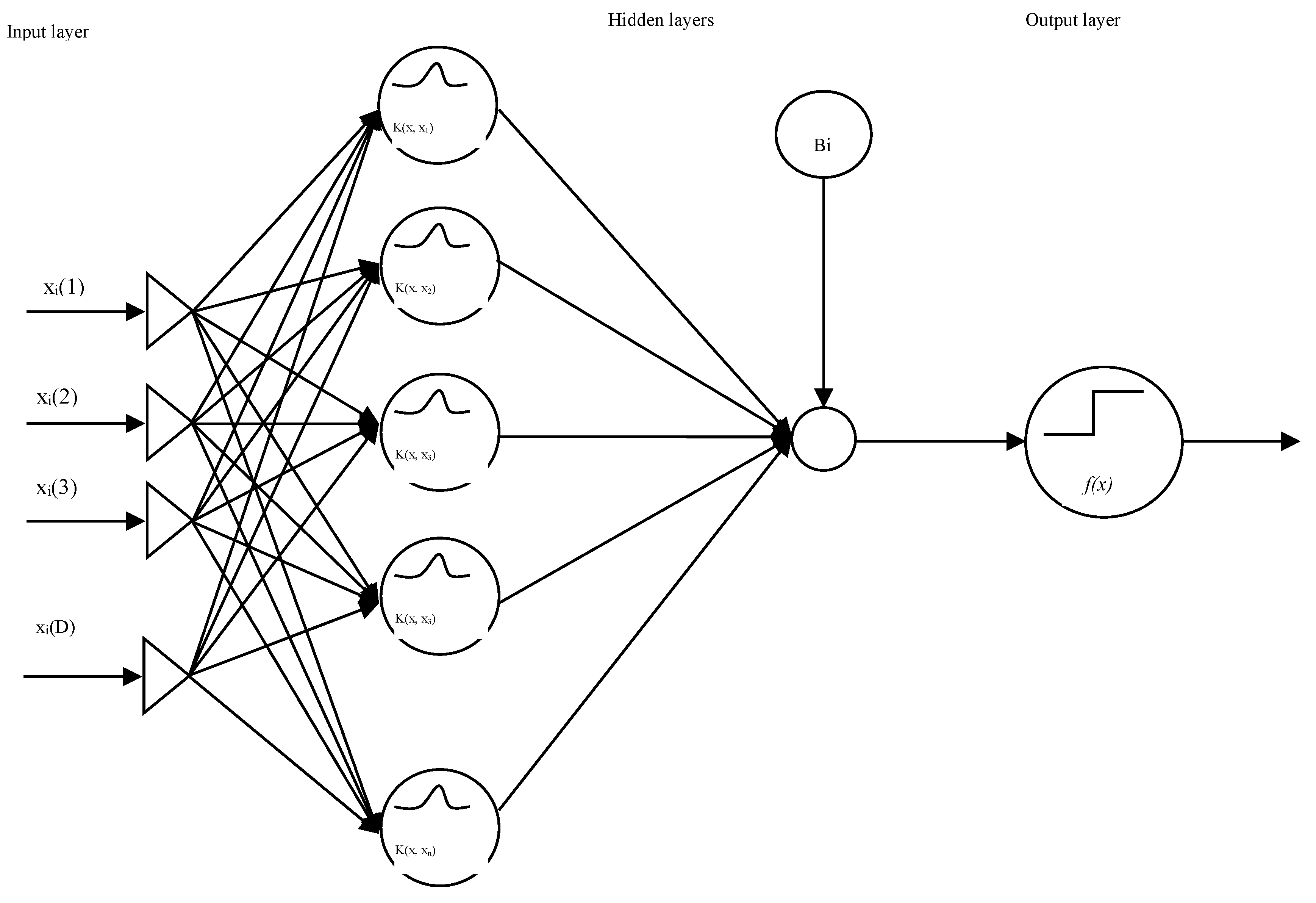
Figure 3.
The Hybrid Genetic Support Vector Machines optimized in GAs on all the layers with or without Cross Validation.
Figure 3.
The Hybrid Genetic Support Vector Machines optimized in GAs on all the layers with or without Cross Validation.
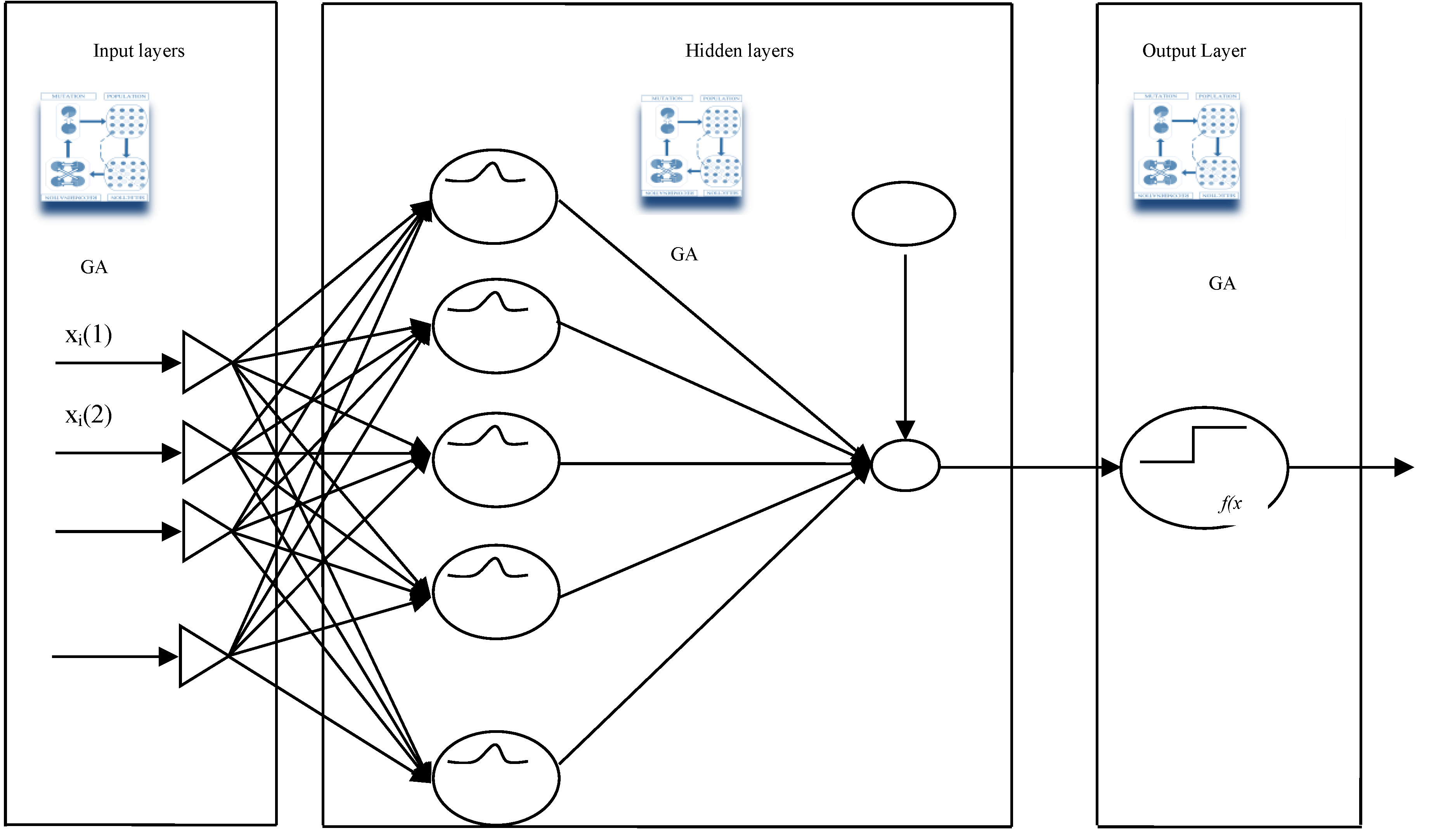
Figure 4.
The Generalised Feed Forward Neural Networks .
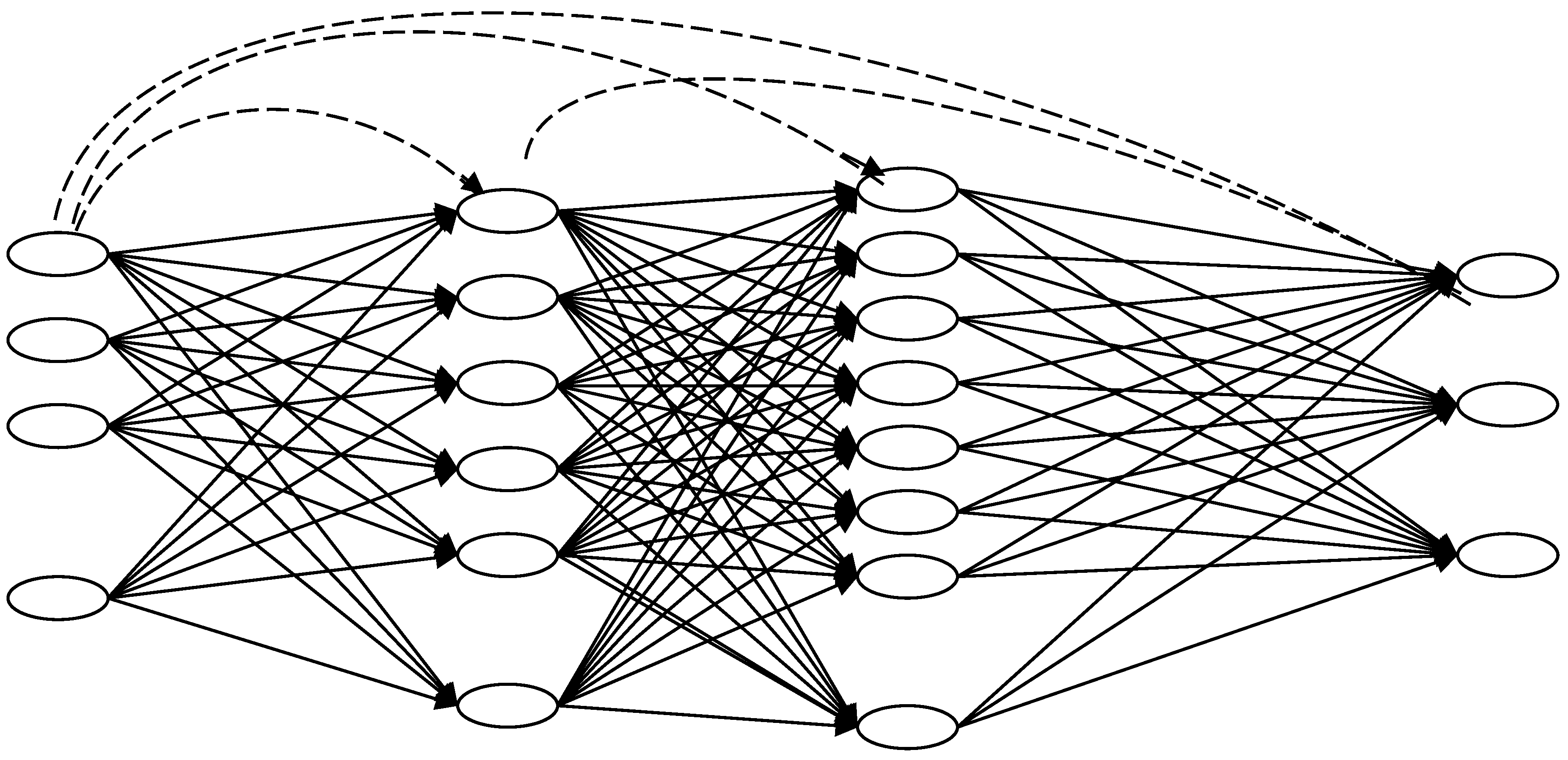
Figure 5.
The Hybrid GFF Net of GA optimization and Cross-Validation in all the layers .
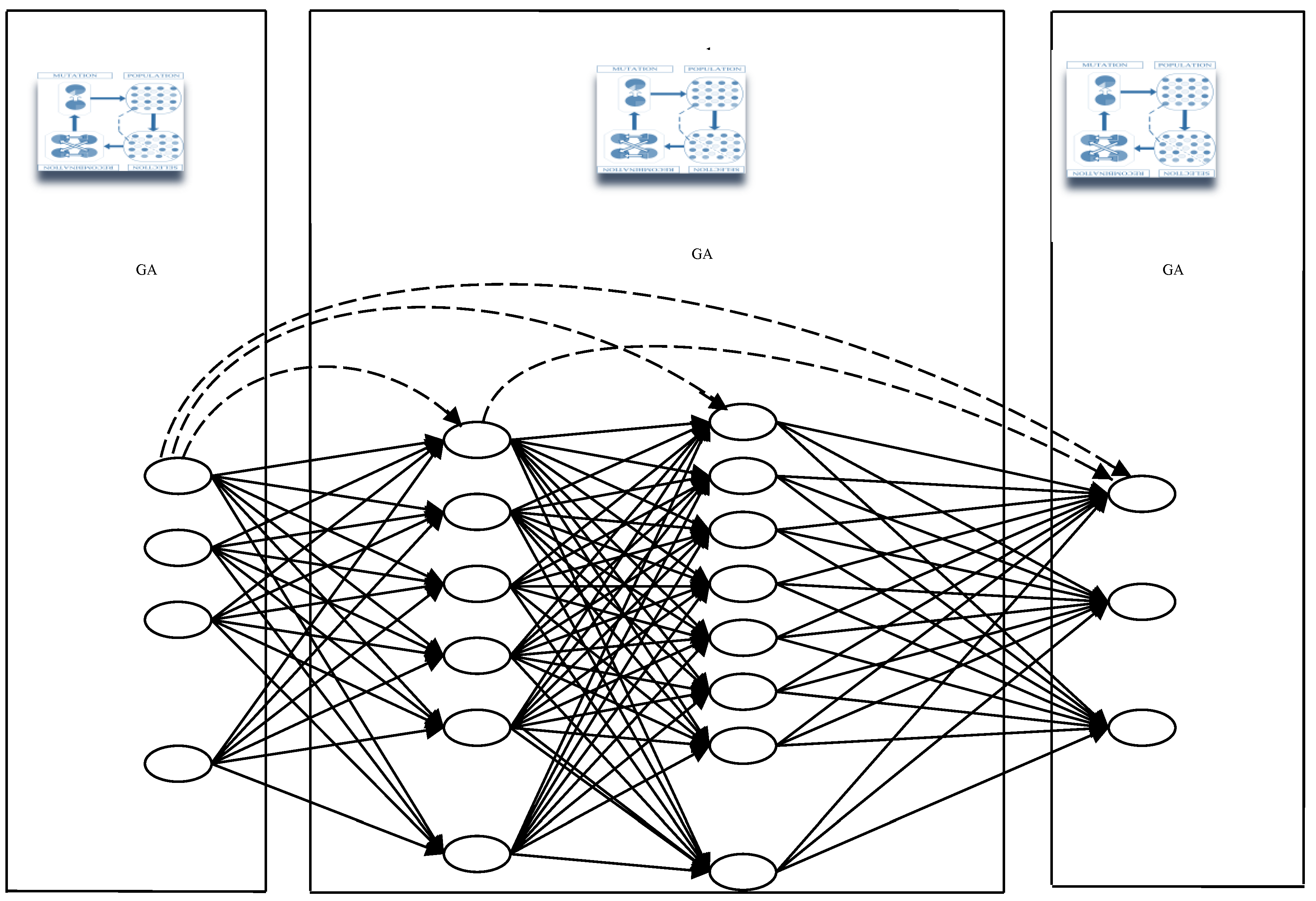
Figure 6.
The Radial Basis Function Networks.
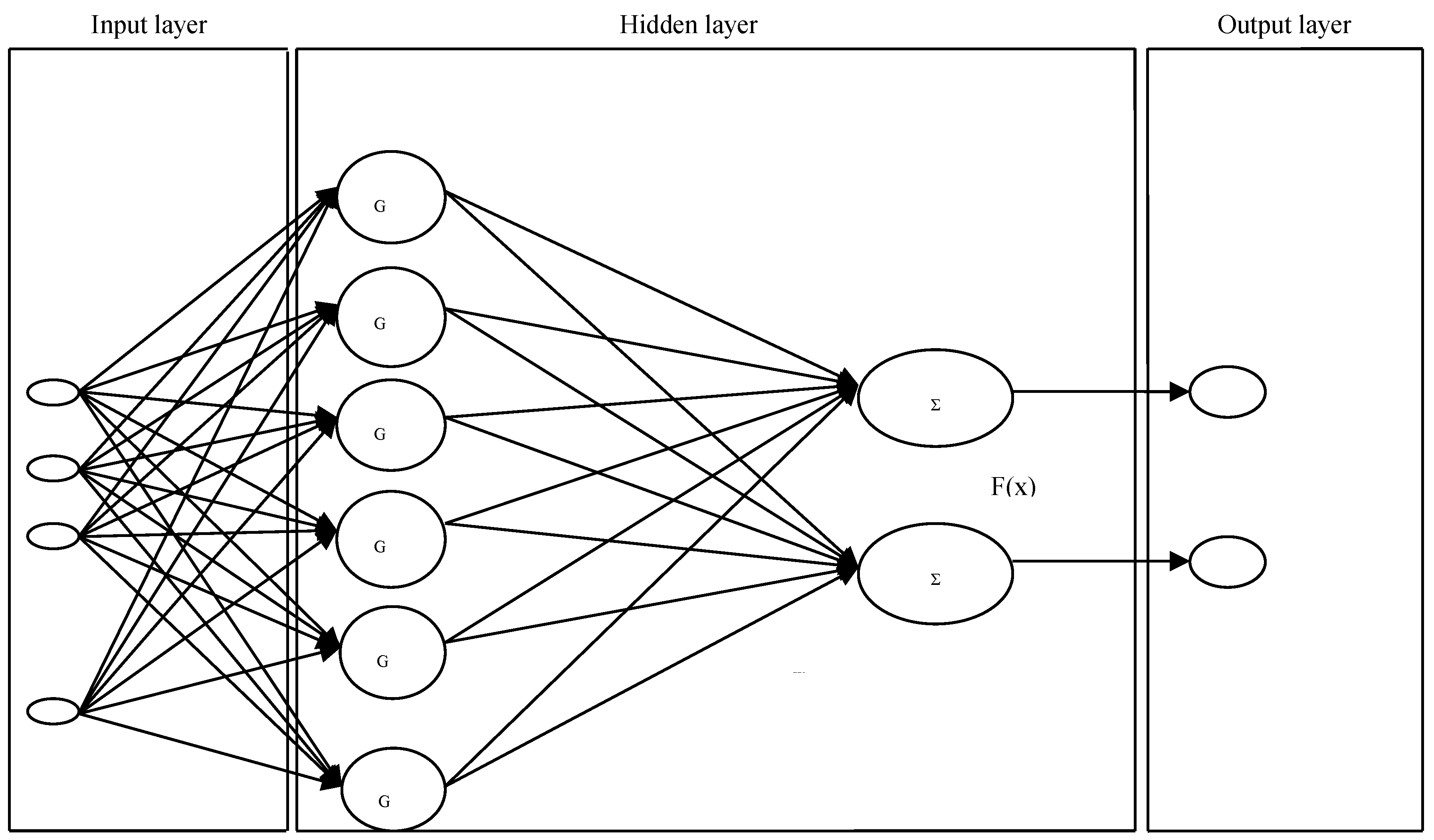
Figure 7.
Hybrid Radial Basis Function in GAs optimisation on input and output layers only.

Table I.
Overall ranking of the optimal GFF models.
| Models | Active Confusion Matrix | Performance | Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Layers | 0→0 | 0→1 | 1→0 | 1→1 | MSE | NMSE | r | %error | AIC | MDL | |||
| GFF input-output GA | 1 | 98.90 | 1.085 | 11.465 | 88.52 | 0.072 | 0.170 | 0.908 | 5.776 | -1907.09 | -1796.44 | 55’ 18’‘ | |
| GFF GA all | 3 | 97.14 | 2.845 | 17.885 | 82.10 | 0.128 | 0.304 | 0.834 | 8.343 | 40259.12 | 284.34 | 2h 44’ 43’‘ | |
| GFF GA all | 1 | 97.56 | 2.425 | 18.805 | 81.18 | 0.133 | 0.315 | 0.827 | 8.243 | -723.475 | -271.82 | 1h 38’ 53’‘ | |
| GFF GA all, | 7 | 96.64 | 3.35 | 19.26 | 80.73 | 0.136 | 0.323 | 0.825 | 9.119 | 1541.07 | 3429.31 | 7h 42’ 32’‘ | |
| CV | 98.32 | 1.67 | 29.355 | 70.63 | 0.149 | 0.353 | 0.812 | 7.073 | 1608.295 | 3495.49 | |||
| GFF NN | 1 | 97.73 | 2.26 | 21.095 | 78.89 | 0.138 | 0.328 | 0.821 | 9.675 | -1225.82 | -1111.95 | 4’‘ | |
| GFF NN, CV | 8 | 98.23 | 1.755 | 26.14 | 73.85 | 0.143 | 0.338 | 0.814 | 9.284 | 709.44 | 2041.35 | 14,5’‘ | |
| CV | 98.23 | 1.755 | 26.14 | 73.85 | 0.143 | 0.338 | 0.814 | 9.284 | 709.44 | 2041.35 | |||
| GFF GA inputs | 10 | 97.98 | 2.005 | 26.6 | 73.16 | 0.144 | 0.341 | 0.812 | 9.469 | 1219.39 | 2873.69 | 1h 27’ 44’‘ | |
| GFF GA all | 8 | 98.57 | 1.42 | 26.6 | 73.39 | 0.140 | 0.329 | 0.821 | 8.329 | 1262.655 | 2959.69 | 5h 59’ 49’‘ | |
| GFF GA all, | 1 | 97.98 | 2.005 | 24.305 | 75.68 | 0.145 | 0.343 | 0.810 | 8.646 | -1219.07 | -1126.3 | 1h 48’ 31’‘ | |
| CV | 98.4 | 1.59 | 24.765 | 75.22 | 0.139 | 0.330 | 0.821 | 8.686 | -1242.55 | -1149.79 | |||
| GFF NN | 10 | 98.65 | 1.34 | 31.185 | 68.80 | 0.147 | 0.348 | 0.810 | 8.454 | 1557.505 | 3419.16 | 9,5’‘ | |
Table II.
The SVMs optimal results, and the MLP, Loukeris et al. (2013).
| Models | Active Confusion Matrix | Performance | Time | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Layers | 0→0 | 0→1 | 1→0 | 1→1 | MSE | NMSE | r | %error | AIC | MDL | ||
| SVM 500 epochs | 100 | 0 | 0 | 100 | 0.035 | 0.072 | 0.999 | 5.436 | 23073.68 | 39305.45 | 1’52’’ | |
| SVM 1000 epochs | 100 | 0 | 0 | 100 | 0.035 | 0.066 | 0.999 | 4.857 | 23016.76 | 39248.53 | 4’11’’ | |
| SVM 500 ep. GA input | 100 | 0 | 0 | 100 | 0.045 | 0.086 | 0.999 | 6.555 | 16159.80 | 27896.09 | 14h39’31’’ | |
| SVM 500 ep GA output | 100 | 0 | 0 | 100 | 0.065 | 0.125 | 0.999 | 6.805 | 23457.92 | 39689.69 | 1h 07’ 34’’ | |
| SVM 1000 ep GA output | 100 | 0 | 0 | 100 | 0.049 | 0.095 | 0.999 | 6.235 | 23253.32 | 39485.09 | 4h23’35’’ | |
| SVM 500 ep GA input C.V. | 100 | 0 | 0 | 100 | 0.023 | 0.045 | 0.999 | 4.013 | 12044.20 | 21524.30 | 26h 56’ 14’’ | |
| CV | 94.29 | 5.69 | 22.01 | 77.98 | 0.309 | 0.591 | 0.949 | 12.728 | 13931.09 | 23409.93 | ||
| SVM 1000 GA output CV | 100 | 0 | 0 | 100 | 0.098 | 0.505 | 0.999 | 6.134 | 23292.73 | 39540.51 | 5h 38’ 12’ | |
| CV | 94.63 | 5.36 | 24.31 | 75.68 | 0.522 | 0.679 | 0.971 | 1.716 | 24663.75 | 40911.52 | ||
| SVM 500 ep GA All. C.V. | 100 | 0 | 0 | 100 | 0.091 | 0.175 | 0.999 | 9.067 | 12375.85 | 21401.51 | 21h 16’ 32’’ | |
| CV | 95.88 | 4.10 | 25.22 | 74.76 | 0.541 | 1.037 | 0.983 | 25.126 | 13646.24 | 22672.40 | ||
| MLP N. N. 1 | 100 | 0 | 98.62 | 1.37 | 0.418 | 0.989 | 0.107 | 19.432 | -468.25 | -374.8 | 15’’ | |
Table III.
RBFs Overall Optimal Results. Loukeris. Eleftheriadis and Livanis (2014b).
| Models | Active Confusion Matrix | Performance | Time | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Layers | 0→0 | 0→1 | 1→0 | 1→1 | MSE | NMSE | r | %error | AIC | MDL | |
| RBF input-output GA 3 | 97.24 | 2.76 | 27.52 | 72.48 | 0.166 | 0.393 | 0.925 | 9.039 | 672.93 | 1912.74 | 5h48’56’’ |
| RBF GA 0 | 98.15 | 1.85 | 39.91 | 60.09 | 0.188 | 0.445 | 0.815 | 13.009 | 37.12 | 820.831 | 5h 02’28’’ |
| RBF inputs GA 0 | 97.73 | 2.26 | 46.32 | 53.67 | 0.219 | 0.519 | 0.791 | 12.383 | 282.78 | 1154.02 | 4h 19’42’’ |
Table IV.
Overall Optimal Results on GFFs, SVMs, RBFs MLPs, Loukeris et al. (2013), Loukeris et al.(2014b).
Table IV.
Overall Optimal Results on GFFs, SVMs, RBFs MLPs, Loukeris et al. (2013), Loukeris et al.(2014b).
| Models | Active Confusion Matrix | Performance | Time | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Layers | 0→0 | 0→1 | 1→0 | 1→1 | MSE | NMSE | r | %error | AIC | MDL | ||
| GFFinput-output GA1 | 98.90 | 1.08 | 11.46 | 88.52 | 0.072 | 0.170 | 0.908 | 5.776 | -1907.09 | -1796.44 | 55’ 18’‘ | |
| SVM 500 ep GA in, C. V. | 100 | 0 | 0 | 100 | 0.023 | 0.045 | 0.999 | 4.0133 | 12044.20 | 21524.3 | 26h 56’ 14’’ | |
| CV | 94.29 | 5.69 | 22.01 | 77.98 | 0.309 | 0.591 | 0.949 | 12.728 | 13931.09 | 23409.9 | ||
| SVM 500 epochs | 100 | 0 | 0 | 100 | 0.035 | 0.072 | 0.999 | 5.4367 | 23073.68 | 39305.4 | 1’52’’ | |
| SVM 1000 epochs | 100 | 0 | 0 | 100 | 0.035 | 0.066 | 0.999 | 4.8573 | 23016.76 | 39248.5 | 4’11’’ | |
| SVM 500 ep GA input | 100 | 0 | 0 | 100 | 0.045 | 0.086 | 0.999 | 6.5558 | 16159.80 | 27896.0 | 14h39’31’’ | |
| SVM 1000 ep GA output | 100 | 0 | 0 | 100 | 0.049 | 0.095 | 0.999 | 6.2354 | 23253.32 | 39485.0 | 4h23’35’’ | |
| SVM 500 ep GA output | 100 | 0 | 0 | 100 | 0.065 | 0.125 | 0.999 | 6.8050 | 23457.92 | 39689.6 | 1h 07’ 34’’ | |
| SVM 1000 ep.GA out CV | 100 | 0 | 0 | 100 | 0.098 | 0.505 | 0.999 | 6.1344 | 23292.73 | 39540.5 | 5h 38’ 12’ | |
| CV | 94.63 | 5.36 | 24.31 | 75.68 | 0.522 | 0.679 | 0.971 | 1.7162 | 24663.75 | 40911.5 | ||
| SVM 500 ep GA All, CV | 100 | 0 | 0 | 100 | 0.091 | 0.175 | 0.999 | 9.0672 | 12375.85 | 21401.5 | 21h 16’ 32’’ | |
| CV | 95.88 | 4.10 | 25.22 | 74.76 | 0.541 | 1.037 | 0.983 | 25.126 | 13646.24 | 22672.4 | ||
| RBF input-output GA 3 | 97.24 | 2.76 | 27.52 | 72.48 | 0.166 | 0.393 | 0.925 | 9.039 | 672.93 | 1912.74 | 5h48’56’’ | |
| GFF GA all 3 | 97.14 | 2.84 | 17.88 | 82.10 | 0.128 | 0.304 | 0.834 | 8.3435 | 40259.12 | 284.345 | 2h 44’ 43’‘ | |
| GFF GA all 1 | 97.14 | 2.845 | 17.88 | 82.10 | 0.128 | 0.304 | 0.834 | 8.3435 | 40259.12 | 284.345 | 1h 38’ 53’‘ | |
| RBF GA All 0 | 98.15 | 1.85 | 39.91 | 60.09 | 0.188 | 0.445 | 0.815 | 13.00 | 37.12 | 820.831 | 5h02’28’’ | |
| RBF inputs GA 0 | 97.73 | 2.26 | 46.32 | 53.67 | 0.219 | 0.519 | 0.791 | 12.383 | 282.78 | 1154.02 | 4h19’42’’ | |
| MLP N. N. 1 | 100 | 0 | 98.62 | 1.37 | 0.418 | 0.989 | 0.107 | 19.432 | -468.25 | -374.8 | 15’’ | |
This model has a wider approach on the stock market assets. Due to limitations of data we examined private companies. The investor can select a variety of assets (common, preferred, private, bonds, treasury bills).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Making Impact on Common Financial Factors Affecting Liquidity Ratio Based on Greedy Approach through Price Movement in Stock Market
Prakash P
et al.
,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








