Preprint

Article

Computing Interface Curvature from Height Functions using Machine Learning with a Symmetry-preserving Approach for Two-phase Simulations

Altmetrics

Downloads

100

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 May 2024

Posted:

30 May 2024

You are already at the latest version

Alerts

Abstract

The volume of fluid (VOF) method is a popular technique for the direct numerical simulations of flows involving immiscible fluids. A discrete volume fraction field evolving in time represents the interface, in particular, to compute its geometric properties. The height function method (HF) is based on the volume fraction field, and its estimate of the interface curvature converges with second-order accuracy with grid refinement. Data-driven methods have been recently proposed as an alternative to computing the curvature, with particular consideration for a well-balanced input data set generation and symmetry preservation. In the present work, a two-layer feed-forward neural network is trained on an input data set generated from the height function data instead of the volume fraction field. The symmetries for rotations, reflections, and the anti-symmetry for the phase swapping have been considered to reduce the number of input parameters. The neural network, establishing a correlation between curvature and height function values, can efficiently predict the local interface curvature. We compare the trained neural network to the standard Height Function method to assess its performance and robustness.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Flows with immiscible fluids, such as water and air, are common in natural phenomena and engineering applications. A wide range of spatial scales is usually observed, ranging from meters, as in sea waves, to microns, as in atomizing jets. A popular approach to deal with these flows, which require the computation of an interface evolving in time, is the one-fluid formulation of the Navier-Stokes equations for incompressible flows, where the different fluids are treated as one fluid with material properties that may change abruptly at the interface. The surface tension force, usually located at the interface, is added to the momentum equation as a source term. When the one-fluid formulation is combined with an interface capturing method, a marker function

f (x, t)

is required to distinguish the different fluids and to compute the geometric properties of the interface, namely, the interface unit normal

n

and the local curvature

κ

. The surface tension force

F_{σ}

can then be computed by the volumetric continuum surface force (CSF) model

F_{σ} = σ κ n

, where

σ

is the surface tension coefficient [1]. The position of the interface is updated by solving numerically the following advection equation

\partial_{t} f + u \cdot \nabla f = 0

for the marker function

f (x, t)

with algebraic or geometric methods [2]. Among the interface capturing methods, the volume of fluid (VOF) method considers the discrete volume fraction or “Color” function C to characterize the interface on a computational grid [3]. Grid cells with only one fluid will have

C = 1

C = 0

, according to the presence or lack of the reference phase. The intermediate value,

0 < C < 1

is found in the cells cut by the interface. Discrete spatial derivatives of the volume fraction field are required to compute the local geometric properties of the interface that are very noisy because of their discontinuous nature. Diffusion operators or convolution with a smoothing kernel can be applied to the volume fraction field locally to obtain a more regular

\tilde{C}

field before differentiating it [4]. An outward unit normal vector

n

at each surface point can then be computed by a discrete approximation of the expression

n = - \nabla \tilde{C} / | | \nabla \tilde{C} | |

and the curvature

κ

of the expression

κ = - \nabla \cdot n

. The numerical convergence of these techniques over different grids depends on the type and support of the kernels.

Another approach to compute the curvature of an interface is the height function (HF) method. In two dimensions (2D), the height function can be envisioned as the distance of the points of an interface line from a reference coordinate axis. With the introduction of a continuous formulation, it has been shown analytically that the HF method converges quadratically to the exact values of the unit normal

n

and of the curvature

κ

[5]. The HF data are proportional to a local integral of the volume fraction field, and numerically, on a uniform Cartesian grid, they can be obtained by summing the volume fractions along columns aligned with coordinate directions. A stencil of heights is then used to compute with finite differences the local value of the geometric properties of the interface line.

In the standard approach in 2D, a fixed

7 \times 3

stencil is used for the summation to obtain three consecutive HF values. An adaptive stencil is an efficient alternative that can be considered to compute the curvature when complex topologies are present, as in the case of merging or breakup of interfaces. Furthermore, the standard method is unreliable or even breaks down when the interface radius of curvature is comparable to the grid step. A few hybrid methods have been developed [6] to overcome this issue. Usually, they combine the HF method at high grid resolution with another method at low resolution. One option is a least-squares (LS) method that fits a parabola over a set of interface points [7], and another one is the convolution (CV) method [8]. A branching algorithm is usually required to switch from one method to another.

In recent years, machine learning has been considered to estimate interface properties. In this data-driven approach, a mapping function between input data and output variables is learned from the data. Due to their modular structure, neural networks are, in principle, able to manage complex functional relations. This approach has been used to compute the unit normal vector at the interface from volume fractions [9] and the constant

α

in the linear equation

n \cdot x + α = 0

for Piecewise Linear Interface Construction (PLIC) [10].

When the interface property to be computed is the local curvature

κ

in the reference cell denoted by

(i, j)

, the functional relationship f between

κ

and the nine-volume fractions C around the reference cell

(i, j)

, can be formally stated as

h κ = f (\begin{matrix} C_{i - 1, j + 1} & C_{i, j + 1} & C_{i + 1, j + 1} \\ C_{i - 1, j} & C_{i, j} & C_{i + 1, j} \\ C_{i - 1, j - 1} & C_{i, j - 1} & C_{i + 1, j - 1} \end{matrix}),

(1)

where the local curvature has been multiplied by the constant grid spacing h to make the previous expression non-dimensional. Circular geometries of different radii have been considered to initialize the volume fractions [11]. This approach was extended to three dimensions (3D) by considering a

3 \times 3 \times 3

stencil and spherical segments to initialize the local volume fraction field [12] and a feed-forward neural network with a single hidden layer was employed.

Neural network models are not sensitive to interface symmetries, which can be obtained by a rotation or reflection of the volume-fractions grid, and also to an inversion between the two phases. Symmetric preserving models have been proposed in the context of interface reconstruction [13]. However, other configurations need to be evaluated. With a proper choice of the neural network, the number of configurations in the training dataset for each volume fraction stencil can be reduced in 2D to only 4 interface configurations [14].

In this paper, we develop a machine learning model (ML) that computes the local interface curvature using the height function values. HF configuration symmetry is investigated concerning rotations and reflections together with the convexity or concavity of the interface. As a result, the number of independent parameters for three aligned HF points is reduced to only 2. The proposed model is tested on different shapes and is compared with the same ML model that uses the volume fractions as input data and with the HF model.

In Section 2, the HF method is briefly reviewed along with the invariance of the curvature concerning a few geometric transformations. The neural network model is analyzed in Section 3, including the data generation methodology and the training process. Finally, results are presented in Section 4 followed by conclusions.

2. The Height Function Method

2.1. The Continuous and Discrete Height Function

Consider an interface line that locally can be written in the explicit form

y = g (x)

, and assume that

g (x)

is continuous with its derivatives. The continuous height function

H (x; h)

is defined as

H_{0} = H (x; h) = \frac{1}{h} \int_{x - h / 2}^{x + h / 2} g (s) d s

(2)

The function H represents the mean value of

g (x)

in the given interval of integration of size h. Analogously, the value of the height function in the two adjacent intervals can be denoted as

H_{- 1} = H (x - h; h)

and

H_{+ 1} = H (x + h; h)

, respectively. With these three consecutive values, it is possible to approximate with centered finite differences the value of the first and second derivatives and of the curvature

κ

of the function

g (x)

at point x

H_{x} = \frac{H_{+ 1} - H_{- 1}}{2 h}, H_{x x} = \frac{H_{+ 1} + H_{- 1} - 2 H_{0}}{h^{2}}, κ = \frac{- H_{x x}}{{(1 + H_{x}^{2})}^{3 / 2}}

(3)

It has been shown that these expressions are second-order accurate with the grid spacing h [5].

In a computational grid in 2D with square cells of side h, the discrete height function can be calculated by adding the volume fraction data along a coordinate direction. In the standard height function method (SHF), a fixed 2D stencil is used, usually involving

7 \times 3

cells, where the first digit refers to the number of cells involved in the summation, and the second digit to the number of heights that are necessary to approximate numerically the curvature. With respect to a reference cell

(i, j)

cut by the interface, with volume fraction

C_{i, j}

that satisfies

0 < C_{i, j} < 1

, the summation in the y-direction is along the 1D stencil that extends 3 cells above and below the reference one

H_{i} = \frac{1}{h} \int_{x_{i} - h / 2}^{x_{i} + h / 2} g (s) d s = \frac{1}{h} \sum_{k = - 3}^{k = + 3} C_{i, j + k} h^{2}

(4)

The interface line should cross the column with thickness h within the 1D stencil. This condition can be enforced by requiring that this stencil is bounded by a cell full of fluid on one end,

C = 1

, and an empty one on the other,

C = 0

. This is a sufficient condition for a well-defined height value. The summation is along the coordinate direction with the largest projection along the interface unit normal

n

, which can be computed numerically from the volume fraction field with different alternative methods [2]. However, it is not always possible to find three consecutive well-defined heights along the same direction, in particular, when the local radius of curvature

ρ

is comparable to the grid spacing h,

ρ \sim h

, or when two different interface lines are approaching or separating from each other.

A way to consider this issue is to use the generalized height function (GHF) with an adaptive 1D stencil. In the present study, the maximum extension of the stencil is limited to 5 cells. Concerning Figure 1, the height can be computed in the first two cases but not in the third one, where a stencil with at least 6 cells is required. However, in the last case, the height can probably be computed along the other coordinate direction. The HF value is stored as an offset from the center of the cell

(i, j)

that contains it. An integer flag is set to indicate that the cell contains the HF and its orientation. A different value of the integer flag is used to indicate that a cell does not contain the HF value but that it was involved in the summation, as in the case of Figure 1b, where there are three cut cells, but only one contains the HF value. In isolated cut cells or with very complex local topologies, the midpoint of the Parker-Youngs reconstruction is considered [15]. Once the HF data have been computed, another sweep across the computational domain is required to collect triplets of HF values to compute

n

, the local curvature

κ

and to interpolate these geometric properties of the interface in the cut cells where the HF is not present.

2.2. Symmetry Considerations for the Machine Learning Model

The curvature of an interface should be invariant under a few geometric transformations of the computational grid and the related volume fraction distribution. These transformations include reflections over a coordinate axis or the diagonal lines

y = \pm x

. A rotation of an angle that is a multiple of

π / 2

can be viewed as a sequence of such reflections. Concerning Figure 2, a triplet of HF values of a given color, either red or blue, is clearly invariant with such a rotation.

Furthermore, each red triplet can be obtained from a blue one, and vice versa, by a single reflection over a coordinate axis.

Independently from the sign convention, the curvature should change its sign when we swap the two fluid phases. As shown in Figure 3, when the interface is concave to the reference phase, the midpoint of the segment connecting the two side HF points is inside the phase with a height smaller than the central one; on the other hand, when the interface is convex the midpoint is in the other phase, beyond the central HF point.

For this reason, only the first case is considered in the machine learning model since the curvature is always assumed to be positive so that the two fluids are swapped when necessary.

Each HF point position is stored as an offset for the cell center. When the heights are collected to compute the geometric interface properties, these points are translated to the same local coordinate system. With three consecutive heights aligned along the same direction and the notation of Eq. (2-3), the coordinates of the three HF points are

(- h, H_{- 1})

(0, H_{0})

and

(h, H_{+ 1})

. Lengths are then normalized to the grid spacing h with the origin of the local coordinate system placed on top of the central HF. The updated values of the coordinates of the three points are finally

(- 1, Δ H_{-})

(0, 0)

and

(1, Δ H_{+})

, with

Δ H_{-} = (H_{- 1} - H_{0}) / h

and

Δ H_{+} = (H_{+ 1} - H_{0}) / h

. It is clear that the geometry of the HF triplet is fully described by the two independent parameters

Δ H_{-}

and

Δ H_{+}

. At low resolutions or with very complex topologies, it will be necessary to consider both vertical and horizontal height functions or even the midpoint of the Parker-Youngs reconstruction. In that case the points coordinates after normalization are

(- δ h_{-}, Δ H_{-})

(0, 0)

and

(δ h_{+}, Δ H_{+})

and the number of independent parameters increases to 4.

The machine learning database is constructed only with geometries with a positive curvature value. The points with the highest HF value are always positioned to the left of the central value to preserve the invariance of the curvature to geometric transformations.

3. Neural Network Model

This section describes the machine learning (ML) model used to calculate interface curvatures. The model is the same for all the different training datasets, namely, the input data can be either the values of the color function or the values of the height function. Considering both the color function and the height function data, we try to analyze a complete set of the input data and the performance of the ML model. We describe in detail both the methodology adopted for the training dataset and the structure of the neural network. The results are then compared to those obtained directly with the Height Function method to evaluate its accuracy and performance.

3.1. Data Generation

The quality of the training dataset strongly influences the performance of the machine learning model, so it is fundamental to generate a set that covers as close as possible the whole range of input data that are expected to be found in actual two-phase simulations. To this aim, a large number of circles are generated on a fixed Cartesian grid, each of them characterized by a random position of the center,

(x_{c}, y_{c})

, and a random value of the radius, R, and of the angle,

θ

, to determine a random point on the circumference. This ensures that the position of the interface is arbitrary without any alignment bias. Traditional methods for Direct Numerical Simulations (DNS) of two-phase flows perform accurately for a radius-to-grid ratio

R / h

above 10. However, their performance degrades rapidly as that ratio decreases. Hence, we set the admissible radius range between

R_{\min} = 2 h

and

R_{\max} = 1000 h

, where

h = 1 / 2000

is the fixed grid spacing of the unit square. The radius distribution between these two limiting values can be determined with different approaches. A simple approach is to use a uniform distribution in the radius R, while a more target-oriented approach is to use a uniform distribution in the curvature

κ

that results in a larger density of small radii when it is compared to the region of large radii. The uniform-in-curvature distribution guarantees that the training set spans with similar density all the output values we want to reproduce. On the other hand, in the uniform-in-radius approach, the density of training data with a large radius is comparatively much higher, so it can have unique orientations between the grid and the interface. Nevertheless, we have selected the uniform-in-curvature approach because, as already stated, traditional curvature reconstruction methods generally perform better at smaller curvature values and need a smaller density of training data in that range to achieve a good performance.

The generation of the training data can be summarized in the following procedure:

Set a seed for the random number generator to ensure reproducibility of the sequence of random numbers: we use the standard pseudo-random number generation routine available in the GNU libc library version 2.31 available in many Linux distributions.

The quality of this distribution is somewhat limited but still adequate to generate the training data for machine learning [16].
Generate sets of random values $V_{k}$ : we can assume that they all lay in the interval $[0, 1]$ , or we can convert them to this interval when the generated numbers are integers in a given range.
Set the curvature value: we set $κ = κ_{\min} + V_{1} (κ_{\max} - κ_{\min})$ and determine the radius $R = 1 / κ$ .
Set the position of the circle: we set the center to $(x_{c}, y_{c})$ ,

with $x_{c} = x_{\min} + V_{2} (x_{\max} - x_{\min})$ and $y_{c} = y_{\min} + V_{3} (y_{\max} - y_{\min})$ .
Set the angle value: we set the angle to $θ = 2 π V_{4}$ and determine the point P on the circumference.
Locate the reference grid cell: we locate the reference cell $(i_{P}, j_{P})$ that contains P and consider a square section of the grid around that cell.
Compute the volume fractions: we compute the volume fractions around the reference cell $(i_{P}, j_{P})$ in the square section and store the central $3 \times 3$ block of values in a dataset.
Compute the height functions: we compute the HF around the reference cell $(i_{P}, j_{P})$ in the square section and store the three central values in another dataset.

The heights can be computed along both coordinate directions, i.e., for x and y. When this is possible, that is to say, three consecutive HF values are computed along each direction by adding two separate sets of training data to the dataset.

The volume fraction field is initialized in each square cell of the computational grid with the new version of the Vofi library [17], which requires a user-defined implicit equation of the interface. This version optimizes and introduces a few new features for the first release of the library [18].

Figure 4 shows the distribution of radii with the two different approaches that we have previously described. We have considered

n_{t} = 5 \times 10^{5}

random circles. The total number of cases obtained with the two distributions is quite different. In particular, we have generated

n_{c} = 413, 798

cases with the uniform-in-curvature approach and

n_{r} = 563, 133

cases with the uniform-in-radius approach. As previously stated, with the uniform-in-curvature approach, we have many more cases with circles having a small radius, where often it is not even possible to find three consecutive heights along the same direction,

n_{c} < n_{t}

. On the contrary, with the uniform-in-radius approach, we have many more cases with a large radius, where the three consecutive heights are found along both coordinate directions,

n_{r} > n_{t}

3.2. Treatment of Regular and Non-Regular Cases

As previously stated, when it is possible to find three consecutive HFs along the same coordinate direction, around the central cut cell

(i, j)

containing the discrete height

H_{0}

, the set of input data consists of the six values of the coordinates,

(- h, H_{- 1})

(0, H_{0})

and

(h, H_{+ 1})

, of the three points. Lengths are then normalized. The number of independent parameters, which constitute the input to train the neural network, is reduced to only 2:

Δ H_{-}

and

Δ H_{+}

. This standard case is called a regular one.

In this study, a slightly different neural network has been trained with a second dataset that contains the non-regular cases. These cases occur when three consecutive height points do not exist along the same coordinate direction. To be able to extend the methodology to very high curvatures, we have devised a methodology that combines the vertical and horizontal heights that are available in the

3 \times 3

block of cells centered around the cut cell

(i, j)

, that contains the height

H_{0}

. When the total number of vertical and horizontal heights is equal to three, the coordinates of these three HF points can be written as

(- δ h_{-}, Δ H_{-})

(0, 0)

and

(δ h_{+}, Δ H_{+})

, with 4 independent parameters.

However, a relatively common situation is where we can find two heights in both directions. In that case, the best solution is to consider two heights from one direction and select the third one in the other direction to enlarge the footprint of the selected set. Failure to do so may lead to two points on the interface having heights that are excessively close to each other with a possible inaccurate curvature estimate. As an example, let us consider two horizontal heights on the top two rows that set the coordinates of the first two points at

(0, H_{x, 0})

and

(h, H_{x, 1})

. To obtain the coordinates of the third point, we look first for the vertical height

(- h_{y,}, H_{y, - 1})

in the bottom row of the

3 \times 3

block of cells. This selection leads to a case of non-uniform row widths and forces the neural network to handle a wide range of scenarios. However, as the standard height function method needs to be changed or integrated with another method at low resolution, we do not present that scenario in this paper, where we study only the high-resolution or asymptotic region.

3.3. Neural Network Definition and Training

The machine learning model for the curvature evaluation is based on a two-layer feed-forward neural network with N neurons in the hidden layer and a single neuron in the output layer, as shown in Figure 5. This structure of the network is effective when mapping a continuous set into another [19], as the one we obtain starting from the set of volume fractions or height functions and compute a curvature value. A single output value presence justifies a single neuron in the output layer. The neurons in the hidden layer have an activation function based on the hyperbolic tangent based on the non-linearity in the relation between volume fractions or height functions and curvature. We have tested the network with a different number

N_{n}

of neurons in the hidden layers, with

N_{n} = 25, 50, 75, 100, 125

. The results are not significantly influenced by

N_{n}

when its value is more than 75, as shown in Figure 6. With a smaller number of neurons, the network cannot reproduce suitably the sets of values present in the dataset. Using a large set does not give any appreciable gain while significantly extending the computational time required to train the model. We choose the value

N_{n} = 100

to compare the results with the literature [11].

The input dataset is a

N_{s}

-by-2 or

N_{s}

-by-9 matrix, where

N_{s}

is the number of training tuples. Each tuple is made up of the 2 parameters

Δ H_{-}

and

Δ H_{+}

in the first matrix, or the 9 values of the volume fraction around the central cell

(i, j)

in the other one. In the following,

N_{t}

will represent the value 2 or 9, based on the training dataset under consideration, when no ambiguity is present.

N_{s}

exact curvature values are considered; we will refer to them as the targets

t_{i}

. The output y of the neural network can be written as

y = \sum_{k = 1}^{N_{n}} w_{k}^{0} tanh (\sum_{j = 1}^{N_{t}} w_{k j}^{h} x_{j} + b_{k}^{h}) + b^{0},

(5)

where

w_{k j}^{h}

are the weights associated to the k-th neuron in the hidden layer and j-th input value,

b_{k}^{h}

is the bias of the k-th neuron. The output layer neuron is marked by the superscript 0. The values for

w_{k j}^{h}

and

b_{k}^{h}

are computed during the training. We can then introduce the mean square error (MSE), defined as

MSE = \frac{1}{N_{s}} \sum_{i}^{N_{s}} (t_{i} - y_{i}) .

(6)

This quantity measures the distance between the neural network solutions

y_{i}

and the exact values

t_{i}

. In a typical machine learning framework, the input dataset is split into a training set, a validation set, and a testing set, with weights 70%, 15%, and 15%, respectively. The weights and biases are adjusted to minimize the MSE of the training dataset only. The neural network is implemented in the MATLAB version 2023.1 deep learning toolbox [19] in agreement to the Levenberg-Marquardt algorithm [20,21]. The algorithm is used many times, each of them referred to as an epoch) on the training dataset, measuring the MSE for each training, validation, and testing set. The process is stopped after 6 consecutive iterations when the MSE does not change appreciably, according to a set tolerance, or the number of epochs reaches the threshold of 1000. For all the results shown later in the text, the convergence of the procedure is reached before the threshold, typically around 700–800 epochs.

Other backpropagation algorithms are available in the deep learning toolbox. Their performance was always inferior to the Levenberg-Marquardt neural network model of curvature. Once the neural network has been prepared, all the weights and biases are stored and used without further access to the input dataset.

4. Results

The results obtained through the neural network approach applied to an extensive training dataset created from height function values are studied in this section. We consider randomly generated points on circular shapes, with different radii and angles, arranged on a Cartesian uniform grid with a spacing h. To create a complete dataset distributed evenly within the target limits, we choose a random and uniform distribution of curvatures ranging from

h / R_{m a x} = 0.001

h / R_{m i n} = 0.5

, corresponding to

R_{m a x} / h = 1000

and

R_{m i n} / h = 2

. Both input or output, generated by these distributions, contain

N = 487, 720

instances. The input dataset is organized as a

N \times 6

array of height coordinates, and the output dataset as a

N \times 1

array of curvatures, acting as the target values for our analysis. We remark that the total number of instances N does not equal the number of randomly generated cases because the input dataset ignores the cases where less than 3 heights are found in the

3 \times 3

block of cells.

The data fitting is performed using Matlab with its built-in Neural Network Toolbox. Using a two-layer feed-forward neural approach, we obtain a relationship between curvature and HF with 100 hidden neurons based on a single linear output neuron. The backpropagation process uses the Levenberg-Marquardt algorithm. The neural network is trained by splitting the dataset into three parts: a training set (

70 %

of the data), a testing set (

15 %

of the data), and a validation set (

15 %

of the data), similarly to [11], that we refer to for a detailed explanation of the terminology. The performance is measured using the mean squared error (MSE). The training process ends when the MSE value does not improve for 6 consecutive epochs or the total epoch count reaches 1000. Figure 7 shows the quality of the fit obtained through the training process, considering the dataset with the uniform-in-curvature dataset (on the left) and the uniform-in-radius dataset (on the right). The evaluation involves the comparison of the output, which consists of the curvatures predicted by the neural network, with the target values representing the exact curvatures. For each data subset (training, validation, and testing) and for the entire dataset, a regression line and the correlation coefficient (R) have been calculated. As we can see, in both simulations of Figure 7, R is almost equal to 1, meaning that predicted curvatures by the neural network are less than

1 e - 5

from the target. This indicates good accuracy and a successful fit between the computed and actual curvatures.

In Figure 8, we show the relative error as a function of the angle when computing the curvature using the height function method and the machine learning approach for different sizes of circumference ranging from

20 h

up to

320 h

. With the height function method, the error scales quadratically when the resolution increases. The error increases from angle 0 (where the interface is almost aligned with the computational grid) towards

π / 4

, where the error is the highest due to the interface cutting the grid diagonally. These results are consistent with the theory detailed in [5]. With the machine learning approach, on the other hand, we see that the error does not scale at all with the resolution. The behavior is similar at all resolutions, with a relative error consistent along the angle.

To compare the convergence of different approaches, we use the

L_{2}

and

L_{\infty}

error norms (as defined in [12]), which are shown in Figure 9 for some prescribed circles with given radii. We report the error norms obtained with the Height Function method (HF) and the Machine Learning (ML) approach. In this case, we compare the errors for the HF and ML methods with the constant slope of order 2.

As expected, the Height Function method scales according to the numerical analysis, as shown in [5]. On the other hand, all the machine learning models do not show accuracy improvement with increasing radius resolution. Similar behavior is shown also in [12,14] for different geometries.

5. Conclusions

In this work, we have explored an alternative approach for computing curvature in Volume of Fluid (VOF) simulations by employing machine learning techniques. We have investigated the use of height function data in combination with machine learning to develop a neural network model capable of efficiently predicting local interface curvature. The state-of-the-art Height Function method has been widely used to compute curvature on well-behaving interfaces but it may face loss of accuracy in non-regular cases where three consecutive height points do not exist in any direction.

To overcome this limitation a novel neural network model has been developed training it on the Height Function values themselves. Our approach aims to handle both regular and non-regular cases by creating a synthetic dataset that includes a wide range of interface curvatures. The results show that the neural network achieves a high degree of accuracy, with an optimal alignment between the predicted curvatures and the exact curvatures from the dataset. However, it is worth noting that while the Height Function method scales perfectly with a quadratic slope, the machine learning prediction does not. The machine learning method can therefore achieve satisfactory results in the prediction of curvature but does not offer any improvement with mesh resolution.

The computational cost associated with the Height Function method is typically only a small fraction of the cost of a two-phase flow solver, so, in general, the time reduction that the Machine Learning algorithm would provide does not justify, at this stage, the loss in accuracy with resolution. A case can be made for the ML approach in situations in which the HF method is not robust or accurate enough, i.e. when the radius of the bubble or droplet is close to the mesh spacing. Further analysis should be carried out in this direction, as well as in the improvement of the ML methodology.

Author Contributions

Conceptualization, A.C. and R.S.; methodology, A.C., R.S. and S.L.; software, A.C., R.S. and L.S.; validation, A.C., R.S. and L.S.; formal analysis, A.C., S.M., R.S. and L.S.; investigation, A.C., S.M., R.S. and L.S.; writing—original draft preparation, A.C., S.M., R.S. and L.S.; writing—review and editing, A.C., S.M., R.S. and L.S.

Funding

This research received no external funding.

Data Availability Statement

Dataset available on request from the authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
Tryggvason, G.; Scardovelli, R.; Zaleski, S. Direct Numerical Simulations of Gas–Liquid Multiphase Flows; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
Cummins, S.J.; Francois, M.M.; Kothe, D.B. Estimating curvature from volume fractions. Comput. Struct. 2005, 83, 425–434. [Google Scholar] [CrossRef]
Bornia, G.; Cervone, A.; Manservisi, S.; Scardovelli, R.; Zaleski, S. On the properties and limitations of the height function method in two–dimensional Cartesian geometry. J. Comput. Phys. 2011, 230, 851–862. [Google Scholar] [CrossRef]
Owkes, M.; Desjardins, O. A mesh-decoupled height function method for computing interface curvature. J. Comput. Phys. 2015, 281, 285–300. [Google Scholar] [CrossRef]
Popinet, S. An accurate adaptive solver for surface–tension–driven interfacial flows. J. Comput. Phys. 2009, 228, 5838–5866. [Google Scholar] [CrossRef]
Patel, H.V.; Kuipers, J.A.; Peters, E.A. Computing interface curvature from volume fractions: A hybrid approach. Comput. & Fluids 2018, 161, 74–88. [Google Scholar]
Svyetlichnyy, D. Neural networks for determining the vector normal to the surface in CFD, LBM and CA applications. . Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1754–73. [Google Scholar] [CrossRef]
Ataei, M.; Bussmann, M.; Shaayegan, V.; Costa, F.; Han, S.; Park, C.B. NPLIC: a machine learning approach to piecewise linear interface construction. Comput. & Fluids 2021, 223, 104950. [Google Scholar]
Qi, Y.; Lu, J.; Scardovelli, R.; Zaleski, S.; Tryggvason, G. Computing curvature for volume of fluid methods using machine learning. J. Comput. Phys. 2019, 377, 155–161. [Google Scholar] [CrossRef]
Patel, H.V.; Panda, A.; Kuipers, J.A.M.; Peters, E.A.J.F. Computing interface curvature from volume fractions: a machine learning approach. Comput. & Fluids 2019, 193, 104263. [Google Scholar]
Buhendwa, A.B.; Bezgin, D.A.; Adams, N.A. Consistent and symmetry preserving data-driven interface reconstruction for the level-set method. J. Comput. Phys. 2022, 457, 111049. [Google Scholar] [CrossRef]
Önder, A.; Liu, P.L.F. Deep learning of interfacial curvature: A symmetry-preserving approach for the volume of fluid method. J. Comput. Phys. 2023, 485, 112110. [Google Scholar] [CrossRef]
Parker, B.J.; Youngs, D.L. Two and three dimensional Eulerian simulation of fluid flow with material interfaces. Technical Report 01/92, UK Atomic Weapons Establishment, 1992.
Shacham, H.; Page, M.; Pfaff, B.; Goh, E.J.; Modadugu, N.; Boneh, D. On the effectiveness of address-space randomization. Proceedings of the 11th ACM conference on Computer and communications security, 2004, pp. 298–307.
Chierici, A.; Chirco, L.; Chenadec, V.L.; R. Scardovelli, a.P.Y.; Zaleski, S. An optimized VOFI library to initialize the volume fraction field. Comput. Phys. Commun. 2022, 281, 108506. [Google Scholar] [CrossRef]
Bnà, S.; Manservisi, S.; Scardovelli, R.; Yecko, P.; Zaleski, S. Vofi - A library to initialize the volume fraction scalar field. Comput. Phys. Commun. 2016, 200, 291–299. [Google Scholar] [CrossRef]
Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural network toolbox. User’s Guide, MathWorks 2010, 2, 77–81. [Google Scholar]
Roweis, S. Levenberg-marquardt optimization. Notes, University Of Toronto 1996, 52. [Google Scholar]
Yan, Z.; Zhong, S.; Lin, L.; Cui, Z. Adaptive Levenberg–Marquardt algorithm: A new optimization strategy for Levenberg–Marquardt neural networks. Mathematics 2021, 9, 2176. [Google Scholar] [CrossRef]

Figure 1. One-dimensional adaptive stencil for height computation: a) only three cells are required, (b) the whole stencil is necessary and (c) the stencil is not wide enough to compute the height.

Figure 2. Geometric sectors of a circular interface: each HF triplet of a given color can overlap with another one through a sequence of reflections.

Figure 3. The position of the midpoint connecting the two side HF points is inside the reference phase if the interface is concave (left), it is outside if the interface is convex (right).

Figure 4. Comparison of curvature distribution in the training dataset when using uniform curvature distribution (left) or uniform radius distribution (right) from the same

5 \times 10^{5}

random circles.

Figure 4. Comparison of curvature distribution in the training dataset when using uniform curvature distribution (left) or uniform radius distribution (right) from the same

5 \times 10^{5}

random circles.

Figure 5. Diagram of the neural network.

Figure 6. Mean Square Error as a function of the number of neurons in the hidden layer.

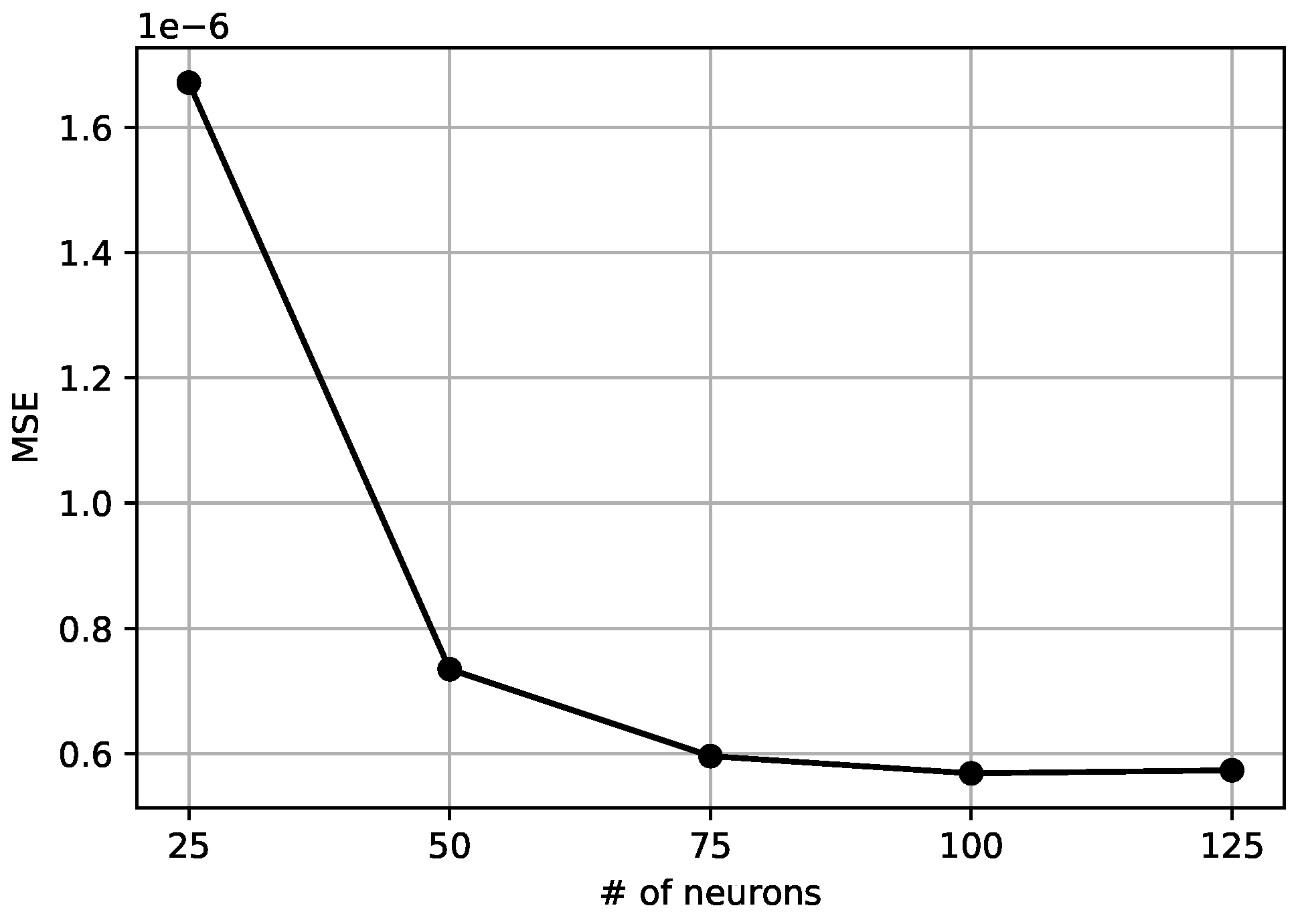
Figure 7. Scatter plots of predicted and target values for training, validation, testing and complete data subset, using the uniform distribution in curvature (left) and in radius (right). The labels report the range of curvatures (between 0.0 and 0.5).

Figure 8. Relative error for circles with 20, 40, 80, 160, and 320

R / h

computed with the height function method (HF, on the top) and the machine learning model (ML, on the bottom).

Figure 8. Relative error for circles with 20, 40, 80, 160, and 320

R / h

computed with the height function method (HF, on the top) and the machine learning model (ML, on the bottom).

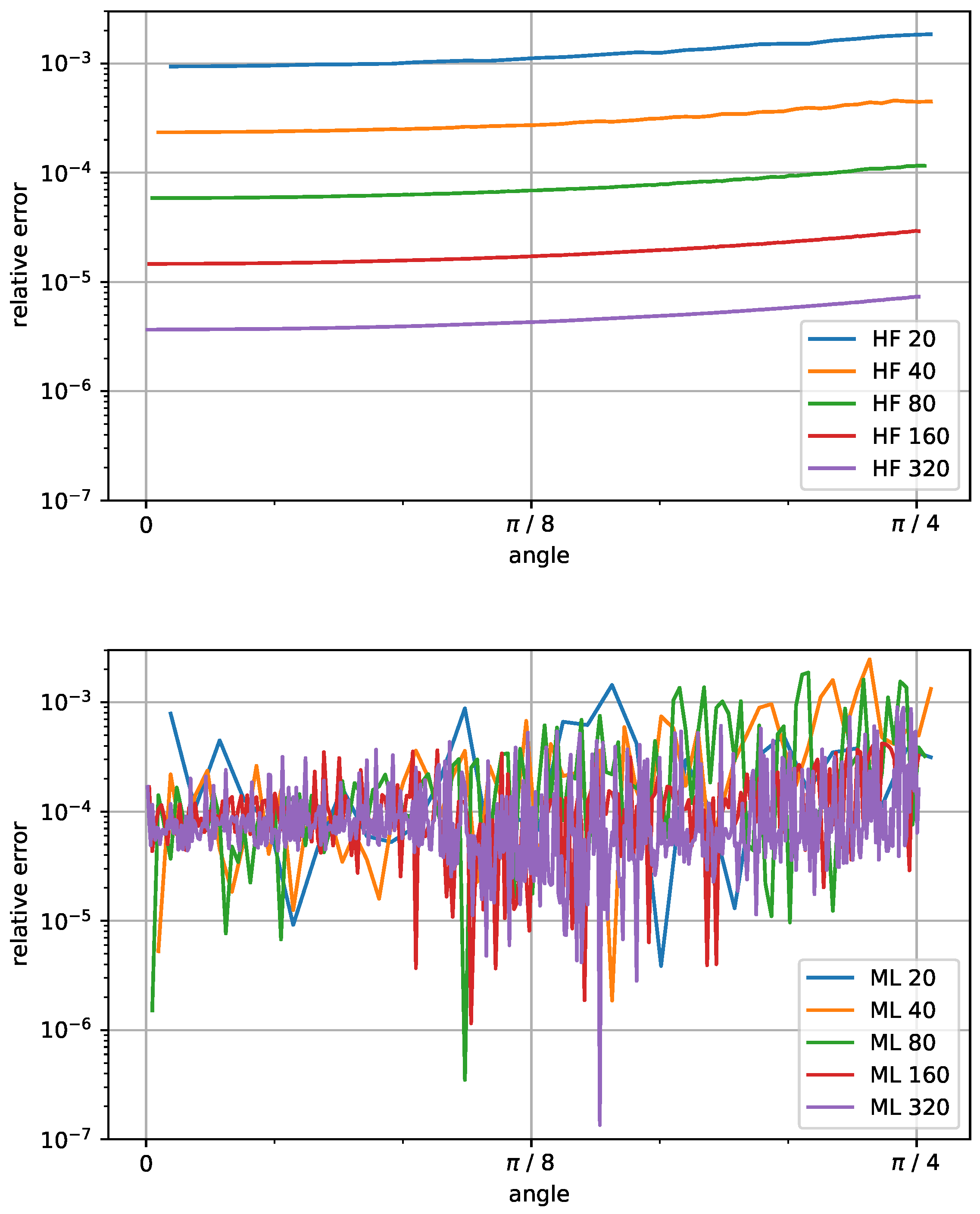
Figure 9. Infinite error (on the top) and mean squared error (on the bottom) for the ML and HF methods with increasing circle resolution.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.