Prerpints.org logo
Preprint
Review

Advances in the Neural Network Quantization: A Comprehen-sive Review

Altmetrics

Downloads

163

Views

85

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 July 2024

Posted:

01 July 2024

You are already at the latest version

Alerts
Abstract
Artificial intelligence technologies based on deep convolutional neural networks and large lan-guage models have made significant breakthroughs in many tasks such as image recognition, target detection, semantic segmentation and natural language processing, but also face the problem of contradiction between the high computational capacity of the algorithms and the limited deployment resources. Quantization, which converts floating-point neural networks into low-bit-width integer networks, is an important and essential technique for efficient deploy-ment and cost reduction in edge computing. This paper analyze various existing quantization methods, showcase the deployment accuracy of advanced techniques, and discuss the future challenges and trends in this domain.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

With the rapid development of artificial intelligence and machine learning technologies, deep learning models have achieved excellent results in many fields, such as Target detection [1,2,3,4], intelligent obstacle avoidance [5], semantic segmentation [6,7,8,9], and situational awareness [10] and. However, the high performance of these models often relies on a large number of parameters and complex computational processes, leading to the big challenges of computational resources and energy consumption in their practical applications. Existing deep learning models still face the shortcomings of requiring high storage, memory bandwidth and computational cost [11]. These shortcomings limit their use on resource-limited devices on many practical applications. Therefore, how to reduce the model size, improve the model running speed, and enable the existing deep models to be applied to embedded platforms is the key to solving the current challenges of deep learning applications. To address this challenge, neural network model quantization techniques have been extensively investigated in recent years to compress neural network models and accelerate their inference process by converting high-precision data to low-precision data [12,13]. For example, quantizing 32-bit multiplication operations to 8-bit can reduce power consumption by about 94.59% (8-bit multiplication operations consume 0.2pj, while 32-bit multiplication operations consume 3.7pj), and the data transfer speed of the quantized model can be increased to 4 times of the original model [14,15]. Neural network model quantization is an important technology that needs to be solved in the field of artificial intelligence, and has urgent application needs and broad application prospects in the fields of embedded high-speed inference and large model compression.
(1) The need for efficient computation of intelligent algorithms on the embedded devices. With the continuous progress of artificial intelligence technology, the application field of neural networks is also expanding. Due to the high computational complexity of intelligent algorithm models represented by neural networks, the contradiction between limited computational resources and the high computational demand of intelligent models seriously restricts the deployment of high-performance neural network models on end-side computing devices, which has become a bottleneck restricting the promotion and application of artificial intelligence technology [16,17,18]. To address this problem, there is an urgent need to carry out research on quantization techniques for neural network models to reduce the storage, data transmission, computational power and power consumption of the models.
(2) Deployment Requirements for Large Language Models. In recent years, big models based on ultra-large-scale text data, represented by BERT [19] and GPT [20,21], have flourished and made substantial progress in tasks such as natural language reasoning and human-computer dialogue, reaching or even surpassing the human level on some datasets. Among them, the most famous is the GPT series of models introduced by OpenAI, whose latest version has reached the scale of 100 billion parameters and is regarded as the most advanced language model. With the rapid increase in the scale of large models, the demand for GPU memory and arithmetic power is getting bigger and bigger, bringing bottlenecks such as storage, access bandwidth, and computation speed, and it is getting more and more difficult for high-performance servers to meet the demand for hardware resources of large models. Deloitte Touche Tohmatsu, one of the world’s Big Four accounting firms, predicts that the market for dedicated chips optimised for generative AI will exceed $50 billion in 2024. The quantization of large models allows companies that rely on them to significantly reduce their need for HPC hardware, which in turn significantly reduces chip procurement and operational costs. Quantizing floating-point large models to 8 bit models for inference computation is also a mainstream practice in the industry today [22,23].
Therefore, the research and development of efficient and low-loss neural network model quantization methods is not only of great significance for promoting the wide application of deep learning techniques, but also has a long-term impact on advancing the development of computer science and artificial intelligence technologies. Neural network quantization can reduce the complexity and size of the model, accelerates the model inference speed, and reduces the resource consumption, which has significant research value in promoting the development of artificial intelligence technology. The main challenge of quantization is how to minimize the loss of computational accuracy caused by the reduction of numerical bit width. A large number of researches have been conducted to try to find quantization strategies suitable for different network architectures and application scenarios, as well as the optimal quantization parameters under different quantization strategies. However, there are still some technical difficulties in this research. In this paper, we compare and analyze the existing neural network model quantization methods, give the deployment accuracy results of the existing advanced methods in the field, and summarize the technical difficulties and development trends of future neural network quantization technology, providing practical quantization technology guidelines.

2. Quantization Fundamentals

Neural network models use floating-point data types, and to achieve high-speed computation, it is necessary to quantize the floating-point neural network models into integer neural networks. As shown in Figure 1, quantization reduces computational cost by decreasing the precision of the data type, which minimises the bit-width of data storage and the amount of data passing through the deep neural network. Computing and storing data at lower bitwidths enables fast inference and reduces energy consumption. The quantization process of a neural network model is to choose a quantization mapping strategy, choose whether to train the model, compute the quantization parameters, generate the inverse quantization parameters of the model, and deploy the inference on the resource-limited devices.
When performing the quantization process on a neural network model, the activation and weight values of the model are restricted to a discrete set of numbers that can have different distributions: uniform or non-uniform. The non-uniform quantization method is the logarithmic distribution [24]. Since inference of neural network models in hardware platforms requires processing of the quantized computational results through certain inverse quantization computational steps to obtain a true floating-point type output. Non-uniform quantization methods have complex inverse quantization computation process and are not friendly to hardware platforms. Most current hardware supports only uniform quantization methods. Therefore, the widely used quantization scheme is the uniform distribution [25] method with uniform step size.
The key issue of quantization is to design a proper quantization mapping function and a proper method to calculate quantization parameters. For uniform quantization, most of the existing quantization approaches asymmetric quantization mapping function or symmetric quantization mapping function [26]. The asymmetric quantization mapping function is as follows:
r = f Q = s · Q + D
Q f − 1 ( r ) = r o u n d r − D s
where f and f − 1 are the quantization mapping function, f − 1 is the inverse function of f, round is the rounding operation, r is the floating point real value, Q is the integer value after quantization, s and D are quantization parameters. s is the scaling factor, and D is the zero point, chosen such that the 0 value would exactly map to quantized values. Symmetric quantization is a simplified version of the general asymmetric case [27]. The symmetric quantizer restricts the quantization parameter D to 0 [28].
In Figure 2, we take symmetric quantization to 8bit as an example. We can see that quantization converts continuous floating-point data into discrete integers, which brings accuracy loss. The quantization parameters are very important for both asymmetric and symmetric quantization and affect the performance of the quantized neural network. The quantization parameters depend on the clipping range, and the scaling factors divides the given range of real values into a number of partitions.
The optimal clipping range for the input is [ m i n i n , m a x i n ], the optimal clipping range for the output is [ m i n o u t , m a x o u t ], the threshold of the weights is thw. How to compute the quantization parameters according to the clipping thresholds is as follows. The quantization parameters s i n , D i n , s o u t , D o u t , s w of a layer are computed according to Equations (3)–(7).
s i n = m a x i n − m i n i n 2 b w i n − 1
D i n = m i n i n − m a x i n 2 b w i n − 1 · round ( ( 2 b w i n − 1 − 1 ) · m i n i n + 2 b w i n − 1 · m a x i n m i n i n − m a x i n )
s o u t = m a x o u t − m i n o u t 2 b w o u t − 1
D o u t = m i n o u t − m a x o u t 2 b w o u t − 1 · round ( ( 2 b w o u t − 1 − 1 ) · m i n o u t + 2 b w o u t − 1 · m a x o u t m i n o u t − m a x o u t )
s w = t h w 2 b w w − 1 − 1
where b w i n , b w o u t and b w w are the bit width of input, output and weight, of which 8 is commonly used.
As shown in Figure 3, the data distribution of neural network model activations and weights is often asymmetric, which poses a significant challenge for selecting clipping range and quantization parameters. A good quantization method should resolve the two following questions to improve the deployment performance. The first question is the trade-off between the accuracy and the difficulty of deployment. The second question is the trade-off between clipping range and quantization resolution, which significantly influences quantization parameters’ computation. There are two main forms of quantization methods: Post Training Quantization [29,30] and Quantization Aware Training [31,32]. Post Training Quantization (PTQ) is the quick quantization of floating-point weights and activations after the model has been trained. Quantization-aware training(QAT) is the process of updating the weights of the model by considering the quantization process during the training process. PTQ is time-saving and convenient, while QAT can get higher accuracy. In addition to PTQ and QAT, the selection of quantization bitwidth and the evaluation of the accuracy loss of deep learning models after quantization are also very important techniques related to quantization. In this paper, we will analyse the development status and challenges of the above related techniques respectively.

3. Quantization Techniques

3.1. PTQ

Post-Training Quantization (PTQ) is an optimization technique applied to neural network models after they have been trained. It is designed to reduce the model’s memory footprint and accelerate inference speed while attempting to maintain the model’s accuracy. The steps of are PTQ are as shown in Figure 4. When the distribution is not gaussian-like, it is difficult for the quantized model to meet the accuracy requirements, especially for complicated tasks with higher accuracy requirements.
The key point for PTQ is how to calculate the quantization parameters, which depends on the clipping range. Usually, a series of calibrations are used as the input of a neural network to compute the typical range of activations [33,34]. A straightforward choice is to use the min/max of the data for the clipping range [33], which may unnecessarily increase the range and reduce the quantization resolution. One approach is to use the i-th largest/smallest value instead of the min/max value as the clipping range [35]. Another approach is to select the clipping range by some kinds of information loss between the original real values and the quantized values [36,37], including KL divergence [38,39], Mean Squared Error (MSE) [40,41,42,43], or entropy [44]. Wei [45] proposes an activation redistribution-based hybrid asymmetric quantization method for neural networks, takes data distribution into consideration and can resolve the contradiction between the quantization accuracy and the ease of implementation. How to choose the optimal quantization parameters and how to reduce the loss of accuracy of the neural network model after quantization is the key problem to be solved.

3.2. QAT

Quantization-Aware Training (QAT) is a technique in deep learning that integrates the quantization process into the training phase of a neural network model. Unlike Post-Training Quantization (PTQ), which applies quantization after the model has been trained, QAT allows the model to learn and adapt to the quantization effects during training. The steps of are QAT are as shown in Figure 5.
QAT is a powerful technique for preparing neural network models for deployment on quantization-sensitive hardware. By training the model to be aware of quantization, it can better adapt and maintain accuracy even with reduced precision. However, most QAT methods use the straight-through gradient estimation (STE) technique, which causes a significant gradient error. To solve this problem, researchers have proposed alternative approaches. PACT [46] explores the impact of activation value trimming on quantization performance. Gong [47] adopts a differentiable tanh function to gradually approximate the quantization function. DoReFa [48] proposes tailoring the weight range prior to quantization. SAT [49] uses the gradient updating process and weight scale adjustment during training to improve quantization performance. Sharpness-Aware Quantization (SAQ) [50] provides a unified view of quantization and Sharpness-Aware Minimization (SAM) by treating them as introducing quantization noises and adversarial perturbations to the model weights. Zhuang [51] proposes a solution by training the low-precision network with a fullprecision auxiliary module and constructs a mix-precision network by augmenting the original low-precision network with the full precision auxiliary module. It is worth noting that although QAT methods can deliver better quantitative performance, they often require large training datasets and significant computational resources, with training times exceeding 100 GPU hours [52].

3.3. The Selection of Quantization Bitwidth

Traditional model quantization methods are to quantize the weight parameters and activation values of the whole model to a fixed bit-width. However, high bit-width quantization ensures high accuracy but also larger memory footprint and computation, while low bit-width quantization has lower accuracy but smaller memory footprint and computation. Because different layers have different redundancy and computational effort, simply assigning the same bit-width does not guarantee optimal network performance. Therefore, Mixed-Precision Quantization (MPQ) is needed to achieve further efficient compression of the model. Wu [53] proposes a search method using differentiable neural network structure search for the bit-width of each layer with no consideration about the inference delay on hardware. Wang [54] proposes the HAQ algorithm, which combines the hardware latency and energy consumption fed back from the hardware simulator to constrain the search for bit-widths at each layer, resulting in a hardware-aware hybrid accuracy policy. In order to quickly allocate the quantization bit-width of each layer, Dong [55] proposes HAWQ, which uses the second-order information of the model parameters to assess the sensitivity of each layer of the model to quantization, and then allocates the bit-width of each layer based on this sensitivity to improve the search efficiency. Dong [56] proposes the EMQ method, which automates the search for mixed-precision configurations with the help of evolutionary algorithms. Tang [57] proposes the SEAM method using small agent datasets to perform a fast search in order to uncover effective MPQ strategies applicable to large-scale training datasets, thus improving the search efficiency and practicality. HAWQv2 [58] enhances model quantization by using second-order information (the Hessian) to determine optimal quantization levels, thereby preserving accuracy while significantly reducing computational and memory costs. Tang [59] proposes the LIMPQ method that can speed up the indicators training process by parallelizing the original sequential training processes. With these learned importance indicators, the MPQ search problem as a one-time integer linear programming (ILP) problem.
Existing hybrid bitwidth allocation methods suffer from the following challenges. Most of the methods do not consider the adaptability to hardware, and since the efficiency and accuracy of the quantized neural network model may vary significantly on different intelligent processors, it is necessary to incorporate hardware feedback on accuracy and speed into the optimisation function of the bit-width search. Meanwhile, these methods either still require a lot of computational resources or are very sensitive to hyperparameters or even initialisation, so it is important to propose a parsimonious and fast search technique.

3.4. The Accuracy Loss Evaluation of the Quantized Models

The quantized model needs to be tested to ensure that the loss of accuracy is within an acceptable range. Some researchers have designed several quantization accuracy loss assessment criteria from the perspective of statistical data analysis to improve the performance of quantization models. Qualcomm [60] designs the Signal to Quantization Noise Ratio (SQNR) to measure the quantization accuracy of different quantization bitwidths. Pengcheng [61] proposes a method to determine the quantization coefficients using the quantization mean square error as a metric, and proposes a method to update the statistical parameters for small networks with serious performance loss. However, the above accuracy loss assessment criteria evaluate the loss from the perspective of data statistics, resulting in the deviation from the actual application data and the lack of practicability to get the accuracy loss of the task. Wang [62] constructs a quantization accuracy predictor based on the highly flexible once for all network [63], which encodes the model structure and quantization strategy to directly predict the accuracy of the quantization model. However, in this method, collecting the quantization dataset takes 16000 GPU hours, which is quite expensive and time-consuming, and the quantization predictor can only predict neural network models of the predetermined structure.
Existing studies on the quantization of neural network models have less systematically analysed the mechanism of computational accuracy loss generated by the quantization process, making it difficult to effectively measure the accuracy loss of different neural network models and different computational tasks after quantization. Therefore, how to accurately measure the accuracy loss of quantized models and how to provide a judgement basis for the quantization method of neural network models, are the challenges that still needs to be solved.

3.5. Quantization of LLMs

The LLM (Large Language Model) is a state-of-the-art deep learning model designed for natural language processing tasks [64]. By integrating the latest quantization techniques, these models achieve significant reductions in computational and memory costs while maintaining high accuracy. However, existing solutions may still face challenges in preserving performance for highly complex tasks and ensuring generalizability across diverse datasets.
Existing quantization methods for large language models (LLMs) can be mainly divided into two categories: weight-only quantization and joint weight and activation quantization. The former compresses a large number of weights into lower bit-widths [65], effectively reducing the memory footprint of the models. The latter quantizes both weights and activations into mixed bit-widths [66], which accelerates matrix multiplications and significantly enhances computational speed.
However, when dealing with significant activation outliers, existing methods often exhibit limited improvements or result in unstable gradients. This challenge highlights the need for more robust quantization techniques capable of effectively managing outliers without compromising stability. Future advancements in this field may focus on adaptive quantization strategies that dynamically adjust bit-widths based on activation distributions, ensuring both efficiency and accuracy. Additionally, exploring novel quantization-aware training methods could further enhance the robustness and generalizability of quantized LLMs, paving the way for their broader application in resource-constrained environments.

4. Experimental Results

4.1. Experimental Setting

We do two sets of experiments, one comparing PTQ methods and the other comparing QAT methods with mixed bit-widths. In order to get the experimental results conveniently, software with fake-quantization [67] modules are used to simulate the accuracy on the neural network accelerator. Fake-quantization models quantization errors in the forward passes. The reason to apply fake-quantization is to quickly simulate the effects of quantization using simulated quantization operations. The purpose of the experiments is to compare the state-of-art quantization methods. The CPU is Intel(R) Core(TM) i7-8700K, 3.70GHz, and the GPU is NVIDIA GeForce GTX1070.
In the PTQ experiment, we utilize classic image classification models GoogleNet and VGG16, the YOLOv1 model from the YOLO series for object detection applications, and the classic Unet model for image segmentation applications. GoogleNet and VGG16 are tested using the publicly authoritative ImageNet dataset to highlight the scientific rigor and fairness of our comparative method. The YOLOv1 model is applied to a custom ship detection dataset, while the Unet model is use with a custom remote sensing image segmentation dataset. The aim is to assess the precision loss of quantized models across targets of various sizes.
In the QAT experiment, we utilize the classic image classification ResNet50, which is evaluated through comparative experiments using the publicly authoritative ImageNet dataset.
The accuracy is verified on software. The evaluation metrics are the accuracy metrics of the model. For image classification application, we use Top-1 Accuracy (the one with the highest probability must be exactly the expected answer). For small target detection application, we use mAP (Mean Average Precision). The calculation of mAP is the same as in the internationally renowned target detection competition PASCAL VOC Challenge. For image segmentation applications, we use the mean Intersection over Union (mIoU) metric to evaluate accuracy.

4.2. Results

First, we compare the PTQ methods [43,44,45] on image classification models, the small target detection model, and the segment model. The results of the PTQ methods are shown in Table 1. Higher accuracy can be achieved due to the use of hybrid asymmetric quantization [45]. Therefore, for the PTQ quantization method, the hybrid quantization method with symmetric weights and asymmetric activation can improve the accuracy of the quantized model as much as possible while ensuring that it is hardware friendly.
Then we compare the QAT methods with mixed bit-widths on image classification model. The results of the QAT methods are shown in Table 2. We compare three methods for mixed-precision allocation and QAT: PACT [46], HAWQv2 [58], and LIMPQ [59].
It is evident that LIMPQ, due to its ability to assign different precision levels to different layers based on their sensitivity, achieves the best results with minimal loss. This advantage allows LIMPQ to create a more balanced trade-off between model size reduction and accuracy retention, leading to the most effective model among the three methods.

5. Future Challenges and Trends

Quantization is an essential technique for model deployment and practical application, helping to balance model performance and efficiency. The main challenge of quantization is how to minimise the accuracy loss caused by the reduction of numerical bit width. From the application requirements, the requirement for the quantization of neural network models is that the bit-width should be set as low as possible to reduce the computational energy consumption and improve the inference speed, while making the loss of accuracy due to quantization as small as possible. In order to solve this problem, the weights of the model and the quantization parameters need to be co-optimised. Co-optimization leads to the problems of how to build a quantization operator that can be derived everywhere, how to evaluate the loss of quantization accuracy, and how to improve the robustness of the model after quantization. In order to solve the problem that the back propagation process of quantization is not derivable during the training process of existing neural network models, it is necessary to model the full-domain differentiable quantization operator; in order to solve the problem that the existing quantization accuracy assessment methods adopt the real measurement method, which requires manual participation and is too time-consuming to be integrated into the collaborative optimization algorithm, it is necessary to study the quantization accuracy loss modelling method; In order to solve the problem of poor performance of existing quantization methods in real intelligent application scenarios, methods to improve the robustness of neural network models after quantization need to be investigated. Therefore, the future development trends of quantization technology is to construct fast adaptive updating of quantization parameters, explore the mechanism of precision loss caused by quantization, and propose automatic compensation and robustness enhancement methods to quantize the neural network models.

Author Contributions

Conceptualization, L.W. and Z.M.; methodology, L.W.; software, C. Y.; validation, C. Y. and Q.Y.; formal analysis, L.W. and Z.M.; investigation, L.W. and C.Y.; resources, L.W. and C.Y.; data curation, C.Y.; writing—original draft preparation, L.W.; writing—review and editing, Z.M.; project administration, Z.M.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ze Liu, Han Hu, Yutong Lin, Zhuliang Yao, Zhenda Xie, Yixuan Wei, Jia Ning, Yue Cao, Zheng Zhang, Li Dong, Furu Wei, and Baining Guo. Swin transformer v2: Scaling up capacity and resolution. In IEEE Conference on Computer Vision and Pattern Recognition, 2022.
  2. Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and Baining Guo. Swin transformer: Hierarchical vision transformer using shifted windows. In IEEE International Conference on Computer Vision, 2021.
  3. Hao Zhang, Feng Li, Shilong Liu, Lei Zhang, Hang Su, Jun Zhu, Lionel M. Ni, and Heung-Yeung Shum. DINO: DETR with improved denoising anchor boxes for end-to-end object detection. In International Conference on Learning Representations, 2023.
  4. Zhuofan Zong, Guanglu Song, and Yu Liu. Detrs with collaborative hybrid assignments training. In International Conference on Computer Vision, pages 6725–6735, 2023.
  5. Zhou XS, Wu WL, “Unmanned system swarm intelligence and its research progresses,” Microelectronics & Computer, 38(12): 1-7, 2021. [CrossRef]
  6. Zhe Chen, Yuchen Duan, Wenhai Wang, Junjun He, Tong Lu, Jifeng Dai, and Yu Qiao. Vision transformer adapter for dense predictions. In International Conference on Learning Representations, 2023.
  7. Yuxin Fang, Wen Wang, Binhui Xie, Quan Sun, Ledell Wu, Xinggang Wang, Tiejun Huang, Xinlong Wang, and Yue Cao. EVA: exploring the limits of masked visual representation learning at scale. In IEEE Conference on Computer Vision and Pattern Recognition, pages 19358–19369, 2023.
  8. Weijie Su, Xizhou Zhu, Chenxin Tao, Lewei Lu, Bin Li, Gao Huang, Yu Qiao, Xiaogang Wang, Jie Zhou, and Jifeng Dai. Towards all-in-one pre-training via maximizing multi-modal mutual information. In IEEE Conference on Computer Vision and Pattern Recognition, pages 15888–15899, 2023.
  9. Wenhai Wang, Jifeng Dai, Zhe Chen, Zhenhang Huang, Zhiqi Li, Xizhou Zhu, Xiaowei Hu, Tong Lu, Lewei Lu, Hongsheng Li, Xiaogang Wang, and Yu Qiao. Internimage: Exploring large-scale vision foundation models with deformable convolutions. In IEEE Conference on Computer Vision and Pattern Recognition, pages 14408–14419, 2023.
  10. Tang L, Ma Z, Li S, Wang ZX, “The present situation and developing trends of space-based intelligent computing technology,” Microelectronics & Computer, 2022, 39(4): 1-8, 2022. [CrossRef]
  11. Bianco, S. , Cadene, R., Celona, L., Napoletano, P., 2018. Benchmark analysis of representative deep neural network architectures. IEEE Access 6, 64270–64277. [CrossRef]
  12. Eirikur Agustsson, Fabian Mentzer, Michael Tschannen, Lukas Cavigelli, Radu Timofte, Luca Benini, and Luc Van Gool. Soft‐to‐hard vector quantization for end‐to‐end learning compressible representations. arXiv:1704.00648, 2017.
  13. Eirikur Agustsson and Lucas Theis. “Universally quantized neural compression.” Advances in neural information processing systems,2020.
  14. Ron Banner, Yury Nahshan, Elad Hoffer, and Daniel Soudry, “Post-training 4-bit quantization of convolution networks for rapid-deployment,” arXiv preprint arXiv:1810.05723, 2018.
  15. Drian Bulat, Brais Martinez, and Georgios T, “High-capacity expert binary networks,” International Conference on Learning Representations, 2021.
  16. Tailin Liang, John Glossner, Lei Wang, and Shaobo Shi. “Pruning and quantization for deep neural network acceleration: A survey,” arXiv preprint arXiv:2101.09671, 2021.
  17. Sahaj Garg, Anirudh Jain, Joe Lou, and Mitchell Nahmias. “Confounding tradeoffs for neural network quantization,” arXiv preprint arXiv:2102.06366, 2021.
  18. Sahaj Garg, Joe Lou, Anirudh Jain, and Mitchell Nahmias. “Dynamic precision analog computing for neural networks,” arXiv preprint arXiv:2102.06365, 2021.
  19. Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. “BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding,” North American Chapter of the Association for Computational Linguistics abs/1810.04805, pp 4171-4186,2018.
  20. Brown Tom, B. , Mann Benjamin, Ryder Nick, Subbiah Melanie, Kaplan Jared. “Language Models are Few-Shot Learners”, Conference on Neural Information Processing Systems 33, pp 1877-1901, 2020.
  21. Xunyu Zhu, Jian Li, Yong Liu, Can Ma, and Weiping Wang. “A Survey on Model Compression for Large Language Models”, CoRR abs/2308.07633, 2023.
  22. Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. “Language Models are Unsupervised Multitask Learners”, 2019.
  23. G. Gallo, D. G. Gallo, D. Lo Presti, D.L. Bonanno, F. Longhitano, D.G. Bongiovanni, S. Reito, N. Randazzo, E. Leonora, V. Sipala, and Francesco Tommasino. “QBeRT: an innovative instrument for qualification of particle beam in real-time”, Journal of Instrumentation pp 11.11, 2016.
  24. Daisuke Miyashita, Edward H Lee, and Boris Murmann. Convolutional neural networks using logarithmic data representation, 2016. arXiv:1603.01025.
  25. Shuchang Zhou, Yuxin Wu, Zekun Ni, Xinyu Zhou, He Wen, and Yuheng Zou. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients, 2016. arXiv:1606.06160.
  26. Gholami A, Kim S, Dong Z, Yao Z, Mahoney MW, et al. (2021). A Survey of Quantization Methods for Efficient Neural Network Inference. arXiv preprint arXiv.2103.13630.
  27. Nagel M, Fournarakis M, Amjad R A, Bondarenko Y, Baalen MV, et al. (2021). A White Paper on Neural Network Quantization. arXiv preprint. arXiv:2106.08295.
  28. Li Y, Dong X, Wang W. (2020). Additive Powers-of-Two Quantization: An Efficient Non-uniform Discretization for Neural Networks. arXiv preprint. arXiv:1909.13144.
  29. Ron Banner, Yury Nahshan, and Daniel Soudry. Post training 4-bit quantization of convolutional networks for rapid-deployment. Advances in Neural Information Processing Systems, 32, 2019.
  30. Zhenhua Liu, Yunhe Wang, Kai Han, Wei Zhang, Siwei Ma, and Wen Gao. Post-training quantization for vision transformer. Advances in Neural Information Processing Systems, 34:28092–28103, 2021.
  31. Benoit Jacob, Skirmantas Kligys, Bo Chen, Menglong Zhu, Matthew Tang, Andrew Howard, Hartwig Adam, and Dmitry Kalenichenko. Quantization and training of neural networks for efficient integerarithmetic-only inference. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2704–2713, 2018.
  32. Yanjing Li, Sheng Xu, Baochang Zhang, Xianbin Cao, Peng Gao, and Guodong Guo. Q-vit: Accurate and fully quantized low-bit vision transformer. Advances in neural information processing systems, 35:34451–34463, 2022.
  33. Jacob B, Kligys S, Chen B, Zhu ML, Tang M, et al. (2018). Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2704-2713.
  34. Yao ZW, Dong Z, Zheng Z, Gholaminejad A, Yu J, et al. (2020). Hawqv3: Dyadic neural network quantization. arXiv preprint. arXiv:2011.10680.
  35. McKinstry, Jeffrey L, Esser, Steven K, R Appuswamy, et al. (2018). Discovering low-precision networks close to full-precision networks for efficient embedded inference. arXiv preprint. arXiv:1809.04191.
  36. Krishnamoorthi, R. (2018). Quantizing deep convolutional net-works for efficient inference: A whitepaper. arXiv preprint 8, 667–668.
  37. Wu H, Judd P, Zhang X, Isaev M, Micikevicius P, et al. (2020). Integer quantization for deep learning inference: Principles and empirical evaluation. arXiv preprint. arXiv:2004.09602.
  38. Migacz, S. (2017). 8-bit inference with TensorRT. GPU Technology Conference 2, 7. URL: https://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf.
  39. Chen T, Moreau T, Jiang Z, Zheng L, Yan E. (2018). TVM: An automated end-to-end optimizing compiler for deep learning. In 13th fUSENIXg Symposium on Operating Systems Design and Implementation (fOSDIg 18), pp. 578–594.
  40. Choukroun Y, Kravchik E, Yang F, Kisilev P. (2019). Low-bit quantization of neural networks for efficient inference. In ICCV Workshops, pp.3009–3018.
  41. Shin S, Hwang K, Sung W. (2016). Fixed-point performance analysis of recurrent neural networks. In 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016, pp. 976–980.
  42. Sung W, Shin S, Hwang K. (2015). Resiliency of deep neural networks under quantization. arXiv preprint. arXiv:1511.06488.
  43. Zhao R, Hu YW, Dotzel J. (2019). Improving neural network quantization without retraining using outlier channel splitting. arXiv preprint. arXiv:1901.09504.
  44. Park E, Ahn J, Yoo S. (2017). Weighted-entropy-based quantization for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5456–5464.
  45. Wei L, Ma Z, Yang C. Activation Redistribution Based Hybrid Asymmetric Quantization Method of Neural Networks[J]. CMES, 2024, 138(1):981-1000. [CrossRef]
  46. J. Choi, Z. Wang, S. Venkataramani, P.I.-J. Chuang, V. Srinivasan, K. Gopalakrishnan, Pact: Parameterized clipping activation for quantized neural networks, 2018, arXiv preprint arXiv:1805.06085.
  47. R. Gong, X. Liu, S. Jiang, T. Li, P. Hu, J. Lin, F. Yu, J. Yan, Differentiable soft quantization: Bridging full-precision and low-bit neural networks, in: Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 4852–4861.
  48. S. Zhou, Y. Wu, Z. Ni, X. Zhou, H. Wen, Y. Zou, Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients, 2016, arXiv preprint arXiv:1606.06160.
  49. Q. Jin, L. Yang, Z. Liao, Towards efficient training for neural network quantization, 2019, arXiv preprint arXiv:1912.10207.
  50. Liu J, Cai J, Zhuang B. Sharpness-aware Quantization for Deep Neural Networks[J]. 2021. [CrossRef]
  51. Zhuang B, Liu L, Tan M, et al. Training Quantized Neural Networks With a Full-Precision Auxiliary Module[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2020. [CrossRef]
  52. Diao H, Li G, Xu S, et al.Attention Round for post-training quantization[J].Neurocomputing, 2024(Jan.14):565.
  53. Wu B, Wang Y, Zhang P, et al. Mixed precision quantization of convnets via differentiable neural architecture search[J]. arXiv preprint. arXiv:1812.00090, 2018.
  54. Wang K, Liu Z, Lin Y, et al. Haq: Hardware-aware automated quantization with mixed precision[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 8612-8620.
  55. Dong Z, Yao Z, Gholami A, et al. Hawq: Hessian aware quantization of neural networks with mixed-precision[C]. Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 293-302.
  56. Dong P, Li L, Wei Z, et al. Emq: Evolving training-free proxies for automated mixed precision quantization[C]. Proceedings of the IEEE/CVF International Conference on Computer Vision. 2023: 17076-17086.
  57. Tang C, Ouyang K, Chai Z, et al. SEAM: Searching Transferable Mixed-Precision Quantization Policy through Large Margin Regularization[C]. Proceedings of the 31st ACM International Conference on Multimedia. 2023: 7971-7980.
  58. Dong, Z. , Yao, Z., Cai, Y., Arfeen, D., Gholami, A., Mahoney, M.W., Keutzer, K.: Hawq-v2: Hessian aware trace-weighted quantization of neural networks. In: Advances in neural information processing systems (2020).
  59. Tang C, Ouyang K, Wang Z, et al. Mixed-Precision Neural Network Quantization via Learned Layer-wise Importance[J]. 2022. [CrossRef]
  60. Sheng, Tao, et al., “A quantization-friendly separable convolution for mobilenets,” 2018 1st Workshop on Energy Efficient Machine Learning and Cognitive Computing for Embedded Applications (EMC2), IEEE, 2018.
  61. P. Feng, L. Yu, S. W. Tian, J. Geng, and G. L. Gong, “Quantization of 8-bit deep neural networks based on mean square error,” Computer Engineering and Design, vol. 43(05), pp. 1258-1264, 2022.
  62. Tianzhe Wang and Kuan Wang and Han Cai and Ji Lin and Zhijian Liu, “APQ: Joint Search for Network Architecture, Pruning and Quantization Policy,” in Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, vol. 2006.08509, pp. 2075-2084, 2020.
  63. Peng Wang, An Yang, Rui Men, Junyang Lin, Shuai Bai, Zhikang Li, “Unifying Architectures, Tasks, and Modalities Through a Simple Sequence-to-Sequence Learning Framework,” in Proc. International Conference on Machine Learning, pp. 23318-23340, 2022.
  64. Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NIPS, 2017.
  65. Tim Dettmers, Artidoro Pagnoni, Ari Holtzman, and Luke Zettlemoyer. Qlora: Efficient finetuning of quantized llms. arXiv preprint arXiv:2305.14314, 2023a.
  66. Xiuying Wei, Yunchen Zhang, Xiangguo Zhang, Ruihao Gong, Shanghang Zhang, Qi Zhang, Fengwei Yu, and Xianglong Liu. Outlier suppression: Pushing the limit of low-bit transformer language models. NeurIPS 2022b, 35, 17402–17414.
  67. Jacob B, Kligys S, Chen B, Zhu M, Tang M, et al. (2017). Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. arXiv preprint. arXiv:1712.05877.
Preprints 110847 g001
Figure 1. Quantization: Turn the 32-bit floating-point neural network to an 8-bit or even lower bit integer network.
Figure 1. Quantization: Turn the 32-bit floating-point neural network to an 8-bit or even lower bit integer network.
Preprints 110847 g001
Preprints 110847 g002
Figure 2. An example of quantization.
Figure 2. An example of quantization.
Preprints 110847 g002
Preprints 110847 g003
Figure 3. The activation distributions of three representative convolutional layers of the Yolo-v3 tiny model. These activation distributions are asymmetric. The horizontal axis is the activation value, and the vertical axis is the activation density.
Figure 3. The activation distributions of three representative convolutional layers of the Yolo-v3 tiny model. These activation distributions are asymmetric. The horizontal axis is the activation value, and the vertical axis is the activation density.
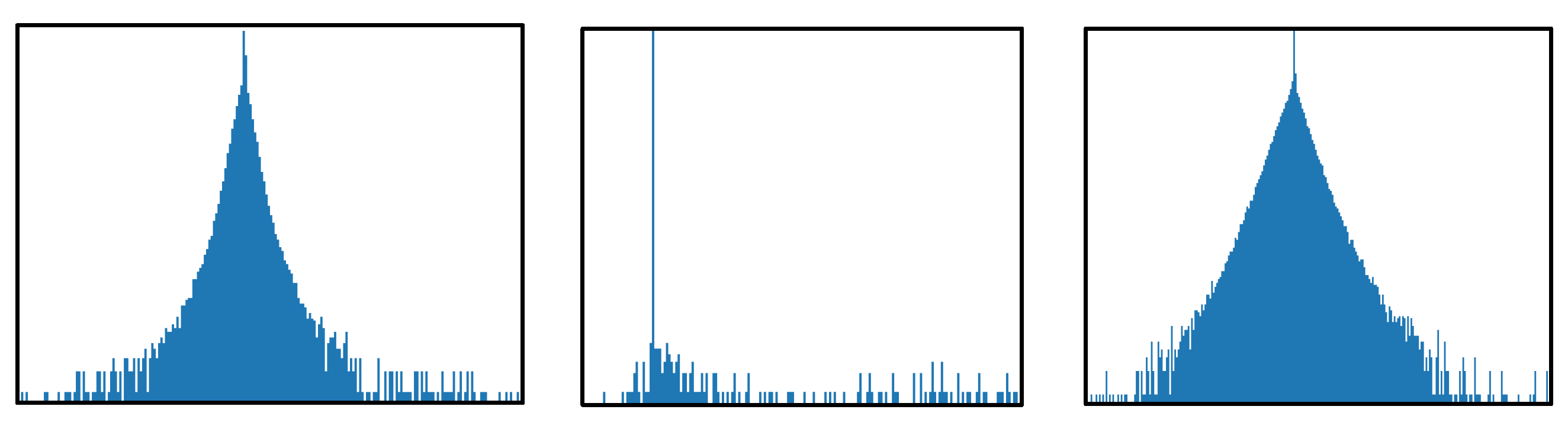
Preprints 110847 g003
Preprints 110847 g004
Figure 4. The steps of are PTQ.
Figure 4. The steps of are PTQ.
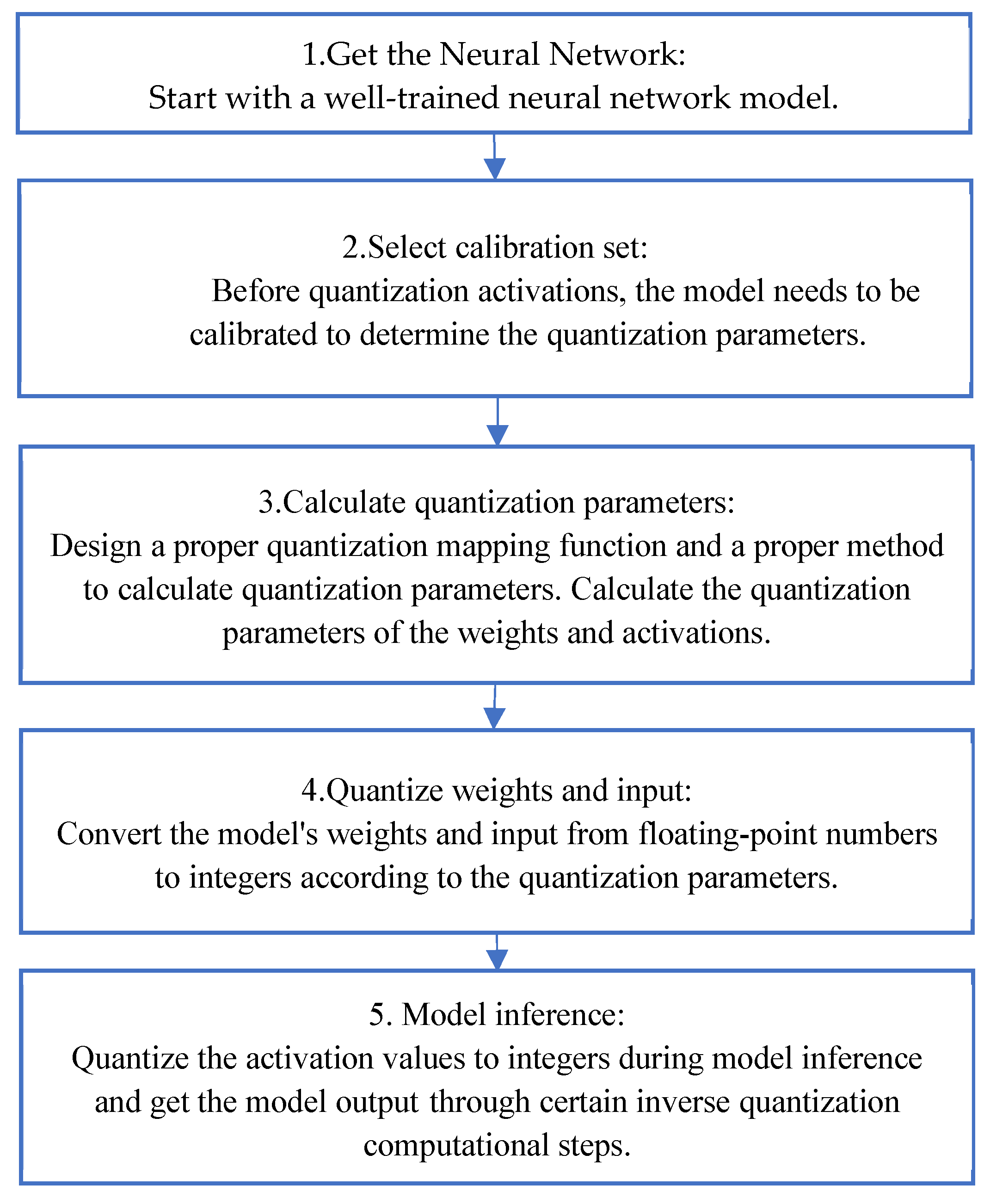
Preprints 110847 g004
Preprints 110847 g005
Figure 5. The steps of QAT.
Figure 5. The steps of QAT.
Preprints 110847 g005
Table 1. Results of the PTQ methods.
Table 1. Results of the PTQ methods.
Task Model PC Accuracy
(FP32)		 Method [44] Method [43] Method [45]
Image Classification GoogleNet 67.04 65.22 65.91 66.65
Image Classification VGG16 66.13 64.72 62.53 65.61
Object Detection yolov1 61.99 59.41 60.94 61.27
Image Segmentation U-net 82.78 82.13 81.71 82.14
Table 2. Results of the mixed-precision allocation and QAT methods for ResNet50 on ImageNet dataset. “W-C” means weight compression rate.
Table 2. Results of the mixed-precision allocation and QAT methods for ResNet50 on ImageNet dataset. “W-C” means weight compression rate.
Method W-bits B-bits Top-1 W-C
PACT [46] 3 3 67.57 10.67x
HAWQv2 [58] 3-Mixed-Precision 3-Mixed-Precision 68.62 12.2x
LIMPQ [59] 3-Mixed-Precision 4-Mixed-Precision 70.15 12.3x
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Research on Convolutional Neural Network Inference Acceleration and Performance Optimization for Edge Intelligence

Yong Liang

et al.

,

2023

ECHO: Energy-Efficient Computation Harnessing Online Arithmetic – a MSDF-Based Accelerator for DNN Inference

Muhammad Sohail Ibrahim

et al.

,

2024

AE-Qdrop: Towards Accurate and Efficient Low-bit Post-training Quantization for Convolutional Neural Network

Jixing Li

et al.

,

2023

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated