The term Air Quality (AQ) pertains to the standard of air, which has a direct impact on the health and well-being of individuals. It is crucial to maintain high Air Quality (AQ), for better health and productivity. Though most of people spend more time indoors nowadays, it is not to be overlooked that the pollutant concentration in indoor air is directly linked to the outdoor air quality. Due to the changes in occupancy patterns, outdated maintenance of ventilation systems, and structural flaws in buildings, the indoor air is significantly polluted; pollutants emitted outdoors enter indoor air through open windows, ventilation systems and infiltration. In this paper, we have proposed a new technique, DTMCPM (discrete-time Markov chain (DTMC) model for the analysis and forecasting of AQ, using the power method). Specialized sensors and equipment to measure different pollutants, such as particulate matter, ozone, nitrogen dioxide, sulfur dioxide, benzene and toluene, are used to collect data by the Institute of Pakistan Air Quality Monitor in various cities; the data is converted to US EPA standard for all pollutant species. This data is used to calculate the transition matrix, steady-state values and mean return rate for the analysis of IAQ. The calculated and actual return rates have been compared and the proposed model is found to have a low average prediction error of 2.356%.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Millions of people are impacted by air pollution each year, which is a significant environmental and public health concern across the globe. Rapid urbanization, industrialization, and an increase in vehicular emissions are significant contributors to the declining air quality. According to the World Air Quality Report 2020, with an average PM2.5concentration of 79.8 g/m3 , which is more than seven times higher than the advised maximum of 10 g/m3 by the World Health Organization (WHO), Pakistan is listed among the top 10 nations with the worst air quality.

Generally, both indoor and outdoor air quality is considered significant components of overall Air Quality (AQ). In a broader context, air quality refers to the standard of air in both indoor and outdoor settings. It constitutes all the factors that can have an impact on human health, comfort, and well-being regarding pollutants, toxins, and the general composition of the air.

The term Indoor Air Quality(IAQ) describes the standard of air inside and around buildings and structures. IAQ significantly affects the health, happiness, and ease of those who live or work indoors. Given the large amounts of time spent by individuals in indoor settings, the tracking, evaluation, and modeling of IAQ are very crucial. According to various research, constant and prolonged exposure to pollutants present in air pollution may lead to numerous diseases and ailments of the respiratory system, cancer, and heart. The short-term effects include headaches, nausea, fatigue, and eye, throat, and nasal irritation. Elevated concentrations of pollutants in the air are the major contributing factor to the declining IAQ. IAQ issues are brought on by the release of gases and particles, into the internal environment, by indoor and outdoor pollution sources. High temperature and humidity, along with a lack of ventilation, by not allowing enough outdoor air in indoor settings to offset indoor sources’ emission, leads to higher concentrations of certain pollutants, which poses a threat to the well-being of a person on a long-term and short-term basis.

Viewing the seriousness of the situation, air monitoring systems have become a need of time, to maintain a healthy and safe indoor environment. Unfortunately, not much heed is paid by the government regarding this matter. Modern buildings are equipped with HVAC (Heating, Ventilation, and Air Conditioning) Systems, which encompass the technology employed for indoor environmental air comfort. The indoor air temperature is maintained by circulating outdoor air, but there is a lack of consideration given to the degradation of IAQ in conjunction with the ambient air quality. Since HVAC Systems have become ubiquitous in buildings, people have started spending more time indoors; to foster a healthy environment for enhanced workplace productivity, and overall increased health and well-being, the constant monitoring of IAQ has become an absolute necessity.

While IAQ plays such an integral part in our lives, Outdoor Air Quality(OAQ) is equally important for our wellness. OAQ refers to the quality of air in an external environment, such as urban, suburban and rural areas. OAQ is impacted by numerous variables, including vehicular emissions, industrial processes, natural resources, and atmospheric conditions. It entails tracking and evaluating pollutant concentrations as well as any potential health effects on people who are exposed to outdoor air. OAQ plays a significant role in helping determine the overall AQ as pollutants released outdoors can enter indoor air through open windows, HVAC, or infiltration. Considering the 2 fact that OAQ directly impacts the pollutants’ concentration in IAQ, in order to attain a safe and healthy environment, it is crucial to consider the overall Air Quality (AQ).

The purpose of this work is to increase the efficiency of the solution provided to develop a smart and safe environment for individuals, by analyzing and predicting the IAQ over a certain period of time using the Discrete Time Markov Chain (DTMC). There are mainly 8 pollutants present in the air :

PM_2.5 (Particulate Matter less than 2.5 micrometres in diameter)

PM₁₀ (Particulate Matter less than 10 micrometres in diameter)

NO₂ (Nitrogen Dioxide)

SO₂ (Sulphur Dioxide)

O₃ (Ozone)

NH₃ (Ammonia)

CO (Carbon Monoxide)

Pb (Lead)

This work focuses on using the concentrations of all the above-mentioned pollutants, along with the concentrations of benzene, toluene and xylene, in the air and predicting the IAQ on the basis of the values calculated. These pollutants enter the indoor environment mostly due to HVAC Systems. All of these pollutants have varying adverse health effects. PM are tiny airborne particles that can penetrate deep into the lungs and cause respiratory and cardiovascular problems. PM_2.5 is particularly harmful because it is so small that it can enter the bloodstream and cause systemic effects such as heart attacks, strokes, and other cardiovascular problems. Primary particulate matter is discharged directly from construction sites, wildfires, wood burning, gravel pits, agricultural activities, and dusty roads. People with asthma or other respiratory diseases are at a higher risk of respiratory issues due to exposure to NO₂, which is primarily emitted from vehicle exhaust and industrial sources. Additionally, it can help form ground-level ozone, a major component of smog that can irritate the respiratory system and worsen other health issues. Paints, cleaners, solvents, and motorized lawn equipment can also contribute to ground-level ozone pollution along with the pollution emitted from cars, power plants, industrial boilers, refineries, and chemical plants. High levels of CO exposure can cause headaches, dizziness, nausea, and even death. It is a colorless and odorless gas that is primarily emitted from incomplete combustion sources, such as vehicle exhaust and poorly maintained heating systems. High levels of NH₃ can cause irritation of the eyes, nose, and throat, and can lead to respiratory problems. It is a colorless gas with a pungent odor that is emitted from agricultural and industrial sources. Exposure to SO₂ can cause respiratory problems, particularly in people with asthma or other respiratory conditions. It is primarily emitted from industrial sources and burning fossil fuels. A child’s exposure to lead can have major negative health impacts that have been well-documented, including:

Slowed growth and development

Damage to the brain and nervous system

The principal origins of lead in the atmosphere are the mining and refining of metal ores, and internal combustion engines used in planes that run on aviation fuel with lead content. Additional sources include facilities that burn waste, companies that provide essential services such as electricity, and manufacturers of lead-acid batteries. The most elevated levels of atmospheric lead concentrations are typically present in the vicinity of lead smelters.

In this work, eigen values and eigen vectors are the tools used for analyzing and predicting the IAQ. The dataset used for forming the transition matrix, for the Discrete-time Markov Chain Model, is collected using specialized sensors and equipment to measure the pollutant concentrations of all the 8 pollutants defined above in this section along with benzene, toluene and xylene. The transition matrix is generated by dividing the concentrations obtained from the dataset into 5 of the 6 Air quality index (AQI) categories i.e., Satisfactory(≤100), Moderate(101-200), Poor(201-300), Very Poor(301-400), and Severe(≥400). It is then used to obtain the steady-state values and mean return period for the prediction of IAQ. The methodology used in this paper has significantly reduced the average prediction error, which is the lowest achieved thus far as per the author's knowledge.

With the world hit by a global pandemic, with its ever-evolving variants, time calls for better air monitoring and predicting systems, to avoid causing any major safety and health issues. This would help save thousands of dollars of treatments by simply indicating and alerting when the AQI is unsafe; helping avoid over-exposure to harmful pollutants present in the air. The technique used in this paper has substantially reduced the prediction error, vitally improving the prediction of the IAQ.

2. Literature Review

There are several research articles that are aimed at developing IAQ monitoring systems, for various uses, but limited research was found that aimed at predicting the IAQ index. In [2] the occurrence of poor air quality is predicted using concentrations from three pollutants- PM_2.5, PM₁₀, and CO. The data collection is done in real-time, with the data being stored in an IoT Cloud- Amazon Elastic Compute Cloud. The state space of the Markov Model is formed using the 5 out of 6 Air Quality Index (AQI) i.e. Satisfactory (≤100), Moderate (101-200), Poor (201-300), Very Poor (301-400) and Severe (≥401). The state space model of the Markov Chain, using AQI is shown in Table. 1.

The mean return period for each steady state is predicted and compared with the actual values for the period, and the average absolute prediction error is 4.75%.

A management system for IAQ for Asthma Management in children is proposed in [3], and the concentrations of PM, VOC, and CO₂ are recorded using a Footbot. Multinomial Logistic Regression Classifier is used to detect smoking and cooking activities, with an accuracy of 95.7%. The stochastic Grey-Box Model Technique is used to detect concentrations of CO₂ in Indoor Air, in [4]. The maximum likelihood method is used to estimate the model parameters after deriving the Stochastic Differential Equations. This approach helps define suitable parameterization for the most simple model identified, for implementation in Predictive Control in Energy Management Systems.

Table 1. IAQ STATE SPACE AND LEVELS OF HEALTH CONCERN.

State	Health Concern	AQI Category
State 1	Satisfactory	≤100
State 2	Moderate	101-200
State 3	Poor	201-300
State 4	Very Poor	301-400
State 5	Severe	>400

PLS and PCA regression are used to develop seasonal and annual prediction models, in [5]. The concentrations of NO, PM_2.5 and PM₁₀ are collected in real-time, from a subway station in Seoul. The difference between pollutant concentrations in different seasons is determined using the MANOVA test. This model takes into consideration the seasonal changes, mainly two factors- temperature and humidity.

Different Machine Learning techniques like linear regression, decision trees, and artificial neural networks [6] are proposed for the collection and analysis of CO₂ concentration, using factors like temperature, humidity, and occupancy. The results are evaluated on the basis of MSE, Root MSE and Coefficient of determination. These results conclude the relationship between air quality levels and activities like cooking, cleaning and exercising, and predict the air quality in a smart environment. In [7], the authors developed a model to predict the concentrations of PM₁₀, NO₂, and SO₂, by using linear regression models using different characteristics like the number of smokers, type of housing, structure and type of primary fuel etc. in 246 urban households in Durban, South Africa. The validation technique used in this model is to Leave Out one cross-validation (LOOCV). All of the above-mentioned models, except [2], required huge data sets in order to make a prediction. Furthermore, the techniques used are not only complex but also require a significant amount of time to train, run and test.

Table 2. AQI CATEGORIES LISTED ALONGSIDE THEIR RANGE.

Range	AQI Category
0-50	Good
51-100	Satisfactory
101-200	Moderately Polluted
201-300	Poor
301-400	Very Poor
401-500	Severe

3. Proposed Technique

Real-time pollutant concentration data is taken at an intervals of a few hours, using specialized sensors and equipment, this data is uploaded to the Air Quality Open Data Platform[8]. Figure 1 shows how this data is collected, processed and eventually used for calculations in this paper. The data for the following pollutants,
PM2.5 (Particulate Matter less than 2.5 micrometers in diameter)

Figure 1. GRAPHICAL MODEL.

PM10 (Particulate Matter less than 10 micrometers in diameter)
NO2 (Nitrogen Dioxide)
O2 (Sulphur Dioxide)
O3 (Ozone)
NH3 (Ammonia)
CO (Carbon Monoxide)
Pb (Lead)
Benzene
Toluene
Xylene

is collected using specialized sensor by the Institute of Pakistan Air Quality Monitor, and stored in an online platform which is represented by an IoT cloud in Figure 1. This data is then used for the prediction of AQI and eventually, the prediction is accessed by the end user. The data collected is from 380 major cities across the globe, which is later on used by numerous institutes and research centres for research purposes. The data collected for Pakistan uses four stations, Karachi, Peshawar, Islamabad and Lahore, and is recorded by the Pakistan Air Quality Monitor- US is graphically represented in Figure 2.

A numerical scale, the Air Quality Index(AQI), is employed to report the level of pollution in the air on a given day; it gauges the degree of cleanliness or contamination in the atmosphere and provides insight into the possible health impacts on individuals. Poor Indoor Air Quality (IAQ) is indicated by a high AQI, which means greater health concern. There are 6 states of the AQI as shown in Figure 3, i.e., Good(0-50), Satisfactory (51-100), Moderate (101-200), Poor (201-300), Very Poor (301-400), and Severe (401-500). Considering the fact that the amount of data for State 1, i.e., Good, was very limited, in this work, we have merged both State 1, Good, and State 2, Satisfactory, into a single State, Satisfactory with a range of ≤100, as shown in Table 3.

These 5 states, Satisfactory (0-100), Moderate (101-200), Poor (201-300), Very Poor (301-400), and Severe (401-500), are used to generate a Transition Matrix. The formation of the transition matrix is discussed in detail in Sub-section 1) Matrix Formation.

In order to ascertain the system's long-term behavior and steady-state probability, the eigenvalue method is used to find the eigenvectors and eigenvalues of the transition matrix. We can utilize the power technique to first determine a matrix's Eigenvalues and Eigenvectors. The dominant eigenvalue and its related eigenvector are found using the iterative power approach. The Dominant Eigen Value is identified to find the steady-state probabilities. Once the eigenvector corresponding to the dominant eigenvalue is obtained, it is normalized to obtain the steady-state probabilities. The steady-state probabilities represent the long-term probability of being in each AQI state. Using the eigenvalue method can provide more accurate and efficient estimates of the steady-state probabilities of an AQI DTMC compared to other methods such as matrix algebra or simulation. After this, the Mean Return Period is predicted to obtain the final results, which are compared to the actual return period values to obtain the average error percentage.

A. AQ Markov Chain Model

A Discrete-time Markov Chain can be used to describe the behavior of a system that jumps from one state to another with a certain probability, as shown in Fig. 6. The probability of this transition depends only on the state that the system is in at the moment; it is independent of the states that the system was in before the current state. For the process to be identified as Discrete-time Markov Chain(DTMC), the following property must be satisfied:

P(Xn+1 = j | Xn = i, Xn-1 = in-1, ..., X0 = i0) = P(Xn+1 = j | Xn = i) (1)

Where X_n represents the AQI at time t, and X_n+1 at time t+1. The Markovian property states that the future AQI, t+1, should only be dependent on the present AQI, t.

Matrix Formulation:

The data collected from the data set is sorted into the different ranges of AQI, by identifying the number of times the data is moving from one state to another state; this is done for each AQI state. The value obtained is divided by the total data available, to obtain the following transition matrix, TM:

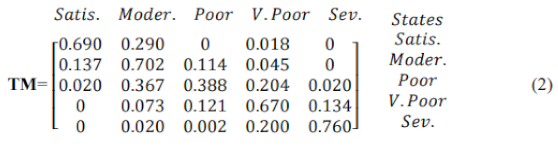
4. Steady AQI States

Steady AQI States represent the long-term probability of each AQI state. There are several methodologies to find the Steady AQI States, from which the method of choice for this paper is Eigen Value Method, as it is more efficient and suitable for larger DTMC models. Eigen Value Method involves finding eigen vectors and eigenvalues of the transition matrix to determine the long-term behavior and steady-state probabilities of the system.

First, to find the Eigenvalues and Eigenvectors of a matrix, we can use the power method. The power method is an iterative algorithm that finds the largest eigenvalue and its corresponding eigenvector.

The power method is an iterative algorithm for computing the dominant eigenvalue and its corresponding eigenvector of a square matrix.

Input : {TM, n}

Output : {V, EV}

TM← Transition Matrix

V← Eigen Vector Matrix

EV← Eigen Value

for i = 1 : n do

V← dot(V, TM) using (2)

end for

V← V / norm(V)

EV← dot(V, dot(TM, V))

Algorithm 1: POWER METHOD

In Algorithm 1, the transition matrix, TM, is given values as shown in (2). The Eigen Vector Matrix, V, is initialized with 1 to avoid any garbage values. The value in V is updated by taking the dot product of V and TM, this is repeated for n iterations; the number depends on the convergence requirements and the desired level of accuracy. The Vector, V, is normalized by dividing by its Euclidean form, i.e. the norm of the vector; the square root of the sum of the squared elements of the vector. The dot product of TM and V, multiplies and sums up the corresponding elements of the vectors; a new matrix is obtained on which the dot product operation is again performed to obtain EV, Eigen Value. The last step represents the power method.

The dominant eigenvalues and eigenvector of the state probability matrix were calculated:

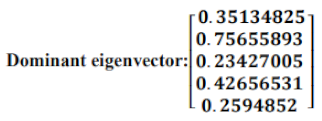
Dominant eigenvalue: 0.998337882239553

To obtain steady-state probabilities from the dominant eigenvector, we need to normalize it. That is, we need to divide each element of the dominant eigenvector by the sum of all its elements. This will give us the probability of being in each state in the long run.

The normalized vectors:

5. Results

This section contains the calculation of Mean Return Period and Actual Return Period; the results are then compared to obtain the average error.

Mean Return Period:

Mean Return Period is the time interval between the occurrences of a certain state, essentially it provides an estimate of the time at which a particular event is most likely to occur.

To calculate the mean return period for each state, we can use the formula:

Mean Return Period = 1 / Normalized Steady State Probability

Assuming that the steady state vector corresponds to the transition matrix that defines the state-to-state transition probabilities, we can use the steady state vector to calculate the mean return period for each state.

Therefore, the mean return period for each state can be calculated as:

Mean return period of state 1 = 1 / 0.17422387 ≈ 5.736

Mean return period of state 2 = 1 / 0.37453858 ≈ 2.670

Mean return period of state 3 = 1 / 0.11584322 ≈ 8.624

Mean return period of state 4 = 1 / 0.21064173 ≈ 4.742

Mean return period of state 5 = 1 / 0.1287526 ≈ 7.768

Actual Return Period:

The Actual Return Period indicates the actual value of probability. It is calculated by finding the State of Occurrence, which is the number of times a state has occurred in the dataset. It is then divided by the total number of data points. The reciprocal of this value gives the actual return period for each state. Table 4. shows the values obtained and calculated using the dataset.

Error Computation:

For error computation, we compared our calculated and actual mean return periods

State 1: 5.8888-5.736/5.888= 0.0259

State 2: 2.7080-2.670/2.7080= 0.014

State 3: 8.33333-8.624= -0.03

State 4: 4.6375-4.742= -0.022

State 5: 7.5711-7.768/7.5711= -0.026

The value of the error is averaged to obtain:

Average Error 2.356%

6. Conclusion & Future Directions

In this work, the Air Quality Index (AQI) is calculated based on the average daily concentrations of eight pollutants (namely PM10, PM2.5, CO, NH3, O3, Pb, SO2, and NO2), which are obtained from the dataset collected by the Institute of Pakistan Air Quality Monitor. The IAQ is then classified into five categories: Satisfactory (≤100), Moderate (101-200), Poor (201-300), Very Poor (301-400), and Severe (>400). To predict the return periods, which is the recurrence interval within which a certain IAQ state is anticipated, for each of the five AQI categories, a DTMCPM model is created utilizing annual AQI data. This method is not only quicker but also simpler and more accurate than the methods or research previously carried out, as discussed in Section II, with an average error of only 2.356%. In the future a real-time monitoring and analysis IoT system is proposed that would take real-time data, which would further improve the efficiency of the proposed model.

References

WHO (2019), Health consequences of air pollution on populations, World Health Organization.
Krati Rastogi and Anurag Barthwal, "An IoT-based Discrete Time Markov Chain Model for Analysis and Prediction of Indoor Air Quality Index," in *Proc. 2020 IEEE Sensors Applications Symposium (SAS)*, March 2020, pp. 1-6.
Marcel Macarulla, Miquel Casals, Matteo Carnevali, Nu´ria Forcada, Marta Gangolells, ”Modelling indoor air carbon dioxide concentration using grey-box models,” Building and Environment, vol. 117, pp. 146- 153, 2017.
U. Jaimini, T. Banerjee, W. Romine, K. Thirunarayan, A. Sheth and M. Kalra, ”Investigation of an Indoor Air Quality Sensor for Asthma Management in Children,” in IEEE Sensors Letters, vol. 1, no. 2, pp. 1-4, April 2017.
MinJeong Kim, B. SankaraRao, OnYu Kang, JeongTai Kim, ChangKyooYoo, ”Monitoring and prediction of indoor air quality (IAQ) in subway or metro systems using season dependent models,” Energy and Buildings, vol. 46, pp. 48-55, 2012.
Deleawe, Seun et al., ”Predicting air quality in smart environments Journal of Ambient Intelligence and Smart Environments,” Journal of Ambient Intelligence and Smart Environments, vol. 2, no. 2, pp. 145-154, 2019.
Nkosana Jafta, Lars Barregard, Prakash M. Jeena, Rajen N. Naidoo, ”Indoor air quality of low and middle income urban households in Durban, South Africa,” Environmental Research, vol. 156, pp. 47-56, 2017.
T. W. A. Q. I. project, “COVID-19 Worldwide Air Quality data,” aqicn.org.

Figure 2. GRAPHICAL REPRESENTATION OF AQI DATA.

Figure 3. STATE TRANSITION DIAGRAM.

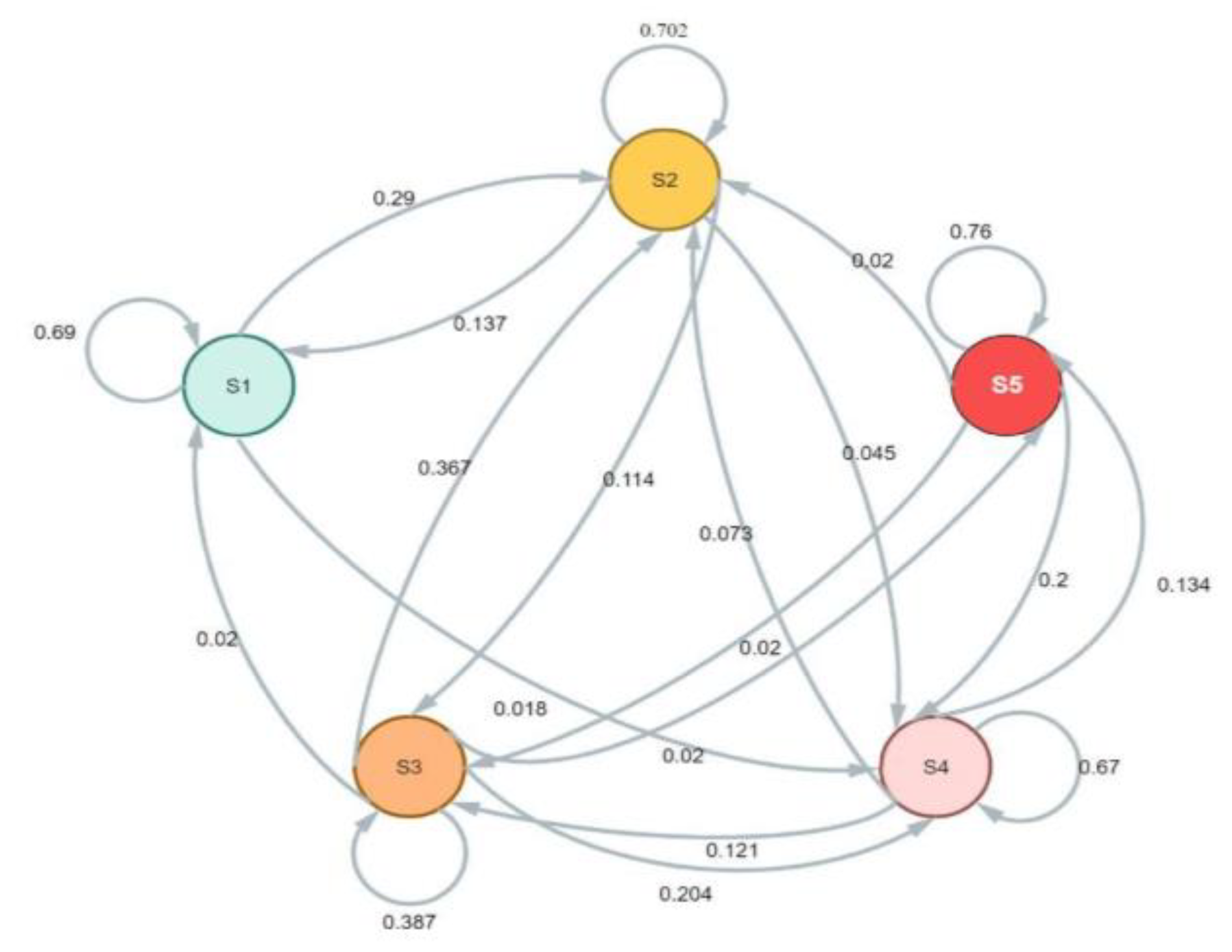
Table 3. IAQ LEVELS AND CORRESPONDING HEALTH CONCERN.

Health Concern	AQI
Satisfactory	≤100
Moderate	101-200
Poor	201-300
Very Poor	301-400
Severe	≥401

Table 4. ACTUAL RETURN PERIOD VALUES.

State Occurrence	Actual Return Period
63	5.888888889
137	2.708029197
42	8.833333333
80	4.6375
49	7.571428571

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.