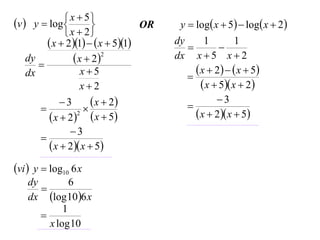SlideShare a Scribd company logo

12 x1 t01 02 differentiating logs (2013)

•
•
N
Nigel Simmons
1 of 35
Downloaded 48 times
Differentiating Logarithms
Differentiating Logarithms y  log f  x 
Differentiating Logarithms y  log f  x  dy f  x   dx f  x 
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  y  log a f  x 
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  y  log a f  x  dy f  x   dx log a  f  x 
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 y  log a f  x  dy f  x   dx log a  f  x 
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x 
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 dy 3 x 2  3 dx x
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 dy 3 x 2  3 dx x 3  x
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 OR 2 dy 3 x  3 dx x 3  x y  log x 3
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 OR 2 dy 3 x  3 dx x 3  x y  log x 3 y  3 log x
Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 OR 2 dy 3 x  3 dx x 3  x y  log x 3 y  3 log x dy 3  dx x
(iii) y  loglog x 
(iii) y  loglog x  1 dy  x dx log x
(iii) y  loglog x  1 dy  x dx log x 1  x log x
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2 
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2  dy 1 1   dx x  3 x  2
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2  dy 1 1   dx x  3 x  2  x  2   x  3   x  3 x  2
(iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2  dy 1 1   dx x  3 x  2  x  2   x  3   x  3 x  2 2x  5   x  3 x  2
v   x  5 y  log   x  2 
 x  5 v  y  log   x  2   x  21   x  51 dy  x  22  x5 dx x2
 x  5 v  y  log   x  2   x  21   x  51 dy  x  22  x5 dx x2  3  x  2   x  22  x  5
 x  5 v  y  log   x  2   x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5 
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2 
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2  dy 1 1   dx x  5 x  2
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x dy 6  dx log 10 6 x y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x dy 6  dx log 10 6 x 1  x log 10 y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
 x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x dy 6  dx log 10 6 x 1  x log 10 y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5 Exercise 12B; 1acf, 2chk, 5acehi, 6b, 7ad, 8acef, 9bd, 10ac, 11, 13a, 14bdfhjl, 15b, 18bdf, 19b, 20af*, 21a* Exercise 12C; 1bdf, 2, 3, 6, 7a, 8, 11, 13, 14, 18*

More Related Content

12 x1 t01 02 differentiating logs (2013)

  • 3. Differentiating Logarithms y  log f  x  dy f  x   dx f  x 
  • 4. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  y  log a f  x 
  • 5. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  y  log a f  x  dy f  x   dx log a  f  x 
  • 6. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 y  log a f  x  dy f  x   dx log a  f  x 
  • 7. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x 
  • 8. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3
  • 9. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 dy 3 x 2  3 dx x
  • 10. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 dy 3 x 2  3 dx x 3  x
  • 11. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 OR 2 dy 3 x  3 dx x 3  x y  log x 3
  • 12. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 OR 2 dy 3 x  3 dx x 3  x y  log x 3 y  3 log x
  • 13. Differentiating Logarithms y  log f  x  dy f  x   dx f  x  e.g. (i) y  log3 x  5 dy 3  dx 3 x  5 y  log a f  x  dy f  x   dx log a  f  x  ii  y  log x 3 OR 2 dy 3 x  3 dx x 3  x y  log x 3 y  3 log x dy 3  dx x
  • 14. (iii) y  loglog x 
  • 15. (iii) y  loglog x  1 dy  x dx log x
  • 16. (iii) y  loglog x  1 dy  x dx log x 1  x log x
  • 17. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2
  • 18. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx
  • 19. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2
  • 20. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2 
  • 21. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2  dy 1 1   dx x  3 x  2
  • 22. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2  dy 1 1   dx x  3 x  2  x  2   x  3   x  3 x  2
  • 23. (iii) y  loglog x  1 dy  x dx log x 1  x log x iv  y  log x  3 x  2 dy  x  31   x  2 1   x  3 x  2 dx 2x  5   x  3 x  2 OR y  log x  3  log x  2  dy 1 1   dx x  3 x  2  x  2   x  3   x  3 x  2 2x  5   x  3 x  2
  • 24. v   x  5 y  log   x  2 
  • 25.  x  5 v  y  log   x  2   x  21   x  51 dy  x  22  x5 dx x2
  • 26.  x  5 v  y  log   x  2   x  21   x  51 dy  x  22  x5 dx x2  3  x  2   x  22  x  5
  • 27.  x  5 v  y  log   x  2   x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5 
  • 28.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2 
  • 29.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2  dy 1 1   dx x  5 x  2
  • 30.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2
  • 31.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
  • 32.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
  • 33.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x dy 6  dx log 10 6 x y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
  • 34.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x dy 6  dx log 10 6 x 1  x log 10 y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5
  • 35.  x  5 v  y  log  OR   x  2  x  21   x  51 dy  x  22  x5 dx x2 3  x  2   x  22  x  5 3   x  2 x  5  vi  y  log10 6 x dy 6  dx log 10 6 x 1  x log 10 y  log x  5  log x  2  dy 1 1   dx x  5 x  2  x  2    x  5   x  5 x  2 3   x  2 x  5 Exercise 12B; 1acf, 2chk, 5acehi, 6b, 7ad, 8acef, 9bd, 10ac, 11, 13a, 14bdfhjl, 15b, 18bdf, 19b, 20af*, 21a* Exercise 12C; 1bdf, 2, 3, 6, 7a, 8, 11, 13, 14, 18*