Homomorphic Encryption

Homomorphic Encryption

Craig Gentry scheme

Why homomorphic encryption?
• Proposed by Rivest, Adleman and Dertouzos
• Confidentiality problems
• Ability to compute over ciphertext instead of
plaintext
• One could use information without knowing the
content of that information
• Privacy garanteed

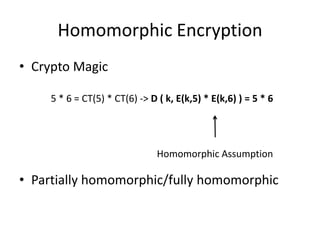
• Crypto Magic

5 * 6 = CT(5) * CT(6) -> D ( k, E(k,5) * E(k,6) ) = 5 * 6

Homomorphic Assumption

• Partially homomorphic/fully homomorphic

• Partially homomorphic schemes
– RSA: CT(x)*CT(y) = (xe mod M) * (ye mod M) = xeye
mod M = (xy)e mod M = CT(x*y), where e is the
exponent key and M the modulus
• p=61;
• q=53;
• N=3233;
• Φ(N)=60*52=3120;
• e=17;
• d=2753;

• Partially homomorphic schemes
– RSA: Obtain 5*6 performing RSA(5)*RSA(6)
• RSA(5) = 517 (mod 3233) = 3086;
• RSA(6) = 617 (mod 3233) = 824;
• 3068*824 = 2542864;
• RSA-1(2542864) = 25428642753 (mod 3233) = 30;
• 5*6 = 30;

• Fully homomorphic schemes
– Craig Gentry scheme
• Based on ideal lattices
– Zaryab Khan scheme
• Based on perfectly colorblind function

Craig Gentry scheme
• Suppose a scheme with a “noise parameter”
attached to each CT;
• Encryption algorithm outputs a CT with a small noise
parameter (say less than n);
• Decryption algorithm only works if noise is less than
some parameter N >> n;
• To compute E(a+b) / E(a*b), include noise;
• This gives a “somewhat homomorphic” scheme.

Craig Gentry scheme
• Now suppose a new algorithm RECRYPT, such that:
– Input: E(a), with noise N’ < N
– Output: E’(a), with noise √N
• “Somewhat homomorphic” -> fully homomorphic!
• Apply RECRYPT to E(a) and E(b) to ensure that the
noise in E(a*b) or E(a+b) is smaller than N
• “Bootstrappable”

Craig Gentry scheme (integers)
• Key: odd integer p > 2N
• Encryption algorithm: given a bit b -> E(b) = c = b +
2x + kp, where x is in [-n/2,n/2] and k is an integer
chosen from some range
• Decryption algorithm: b = (c mod p) mod 2, where (c
mod p) is the noise and belongs to [-n,n]
• Decryption works if b + 2x ∈ [-N,N] ⊂[-p/2,p/2]

• Graig Gentry scheme’s homomorphic assumptions
– Addiction: c1 + c2 = b1+ b2 + 2(x1+x2) + (k1+k2)p =
b1 xor b2 + 2x + kp
• Decryption works if (b1+2x1) + (b2+2x2) is in [-
N,N]
– Multiplication: c1*c2 = b1*b2 + 2(b1x2 + b2x1 +
2x1x2) + kp = b1*b2 + 2x + kp
• Decryption works if (b1+2x1) * (b2+2x2) is in [-
N,N]

• Addition example: 4+4
– CT(100):
22 21 21
• CT(1) = 1 + 2*3 + 5*3 = 22
+22 21 21
• CT(0) = 0 + 2*3 + 5*3 = 21
44 42 42
• CT(0) = 0 + 2*3 + 5*3 = 21
– D(44 42 42):
• D(44) = 44 mod 3 = 2
• D(42) = 42 mod 3 = 0
1000 = 8 = 4+4
• D(42) = 42 mod 3 = 0

• Multiplication example: 4*4
– CT(100):
• CT(1) = 1 + 2*3 + 5*3 = 22
22 21 21
• CT(0) = 0 + 2*3 + 5*3 = 21 ×22 21 21
• CT(0) = 0 + 2*3 + 5*3 = 21 484 924 1365 882 441
– D(484 924 1365 882 441):
• D(484) = 484 mod 3 = 1
• D(924) = 924 mod 3 = 0
• D(1365) = 1365 mod 3 = 0
10000 = 16 = 4*4
• D(882) = 882 mod 3 = 0
• D(441) = 441 mod 3 = 0

Craig Gentry scheme (ideal lattices)
• Replace integers by ideal lattices
• Ideal lattices have many representations or
“bases”
• Bases:
– Good: good to decrypt, bad to encrypt
– Bad: bad to decrypt, good to encrypt
• Public key scheme, where good bases are
private keys and bad bases are public keys

Cryptography over lattices
• L = ζ(B) = {Bc : c ∈ Zk}, B ∈ Rn×k, where the k
columns of the basis are linearly independent
• NP-hard problems over lattices:
– SVP (shortest vector problem): given a basis for
lattice L of size n, find the shortest nonzero vector
v ∈ L s.t. ||v|| = λ(L);
– CVP (closest vector problem): given a basis for
lattice L of size n and a vector t ∈ Rn, find a
nonzero vector v ∈ L s.t. ||t-v|| ≤ γ;

Cryptography over lattices
• NP-hard problems over lattices:
– SIVP (shortest independent vector problem): like
the SVP, except the output are linearly
independent vectors v1, …, v2 ∈ L of length at
most λ(L);
– BDDP (bounded distance decoding problem):
same as CVP but with the promise that there is a
unique solution.

Craig Gentry scheme
• Why inefficient?
– CT size and computation time increase sharply as
the security level increases;
– 2k security -> CT size and computation time are
high-degree polynomials in k;
– Efforts are being made to reduce the
computational requirements of Craig Gentry
construction

• Nowadays:
– Craig Gentry presented a working implementation
of the fully homomorphic system, including the
bootstrapping function
– Exists a practical application of homomorphic
encryption to a hybrid wireless network
– Perform statistical tests over encrypted data such
as temperature, humidity, etc.
– There are also some practical implementations of
simplifications of this scheme over databases

Problems solved
• Cloud security
• Problems related to personal records like
medical records
• Work with information stored in databases
• Querys to search engines
• …

My Project
• Design an API and include it on a Web Service
that will work over CLOUD platforms
• The API should provide homomorphic
encryption functions to be used
• Create a prototype that will work under the
constructed API

Homomorphic Encryption

More Related Content

Homomorphic Encryption