koordinatsystem

I et rettvinklet koordinatsystem har man to rette linjer (koordinataksene), som skjærer hverandre i rett vinkel. Skjæringspunktet O mellom aksene kalles origo. De to aksene deler planet i fire kvadranter. Den vannrette aksen kalles x-aksen eller abscisse-aksen. Den andre kalles y-aksen eller ordinataksen. På hver akse velges en positiv retning, og en lengdeenhet fastlegges.

Et punkt P i planet angis ved avstanden mellom punktet og de to aksene. Avstanden \(x_0\) fra punktet til \(y\)-aksen kalles \(x\)-verdien eller abscissen til punktet. Den regnes positiv eller negativ etter som skjæringspunktet ligger på den positive eller negative siden av origo. På tilsvarende måte er \(y\)-verdien eller ordinaten \(y_0\) lik avstanden mellom punktet og \(x\)-aksen. Punktet betegnes da ved koordinatene \(x_0, y_0\). Et vanlig rutepapir er et eksempel på et slikt koordinatsystem.

En annen viktig type koordinatsystemer i planet er polarkoordinater. Her bestemmes et punkt P ved avstanden r fra et fast punkt, som kalles polen O, og den vinkelen α (alfa) som linjen OP danner med en fast retning eller akse gjennom O. Avstanden r kalles radius vektor, og vinkelen kalles amplituden.

Sammenhengen mellom de rettvinklede koordinatene \((x,y)\) til et punkt og de polare koordinatene \((r, \alpha)\) er gitt ved ligningene:

\(x = r \cos \alpha\) og \(y = r \sin \alpha\)

Her er \(\cos \alpha\) cosinus til vinkelen \(\alpha\), og \(\sin \alpha\) er sinus til vinkelen.

I homogene koordinatsystemer angis et punkt ved tre koordinater \( (x_1, x_2, x_3)\), men det er bare forholdene x₁:x₃ og x₂:x₃ mellom dem som er av betydning. De homogene koordinatene brukes særlig innen projektiv og algebraisk geometri. De kan oppfattes som punktets avstand fra tre rette linjer som ikke skjærer hverandre i samme punkt.

Ved studium av plane kurver er det ofte praktisk å fremstille kurven som en ligning \(R = f(s)\) mellom buelengden s regnet fra et fast punkt på kurven og krumningsradiusen R. Man kaller s og R kurvens naturlige (engelsk intrinsic) koordinater.

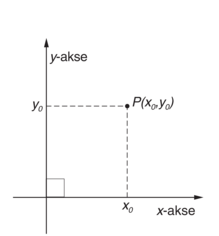
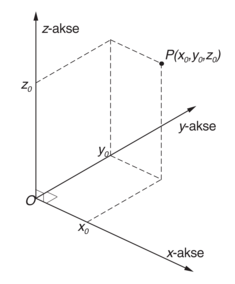
I det tredimensjonale rommet \(\mathbb{R}^3\) er det vanlig å bruke koordinatsystemer som er generaliseringer av koordinatsystemer i planet. Oftest brukes rettvinklede koordinatsystemer, hvor et punkt P bestemmes ved avstandene (x, y, z) fra tre gitte koordinatplan. Disse tre koordinatplanene skjærer hverandre i tre koordinatakser, x-, y- og z-aksene, som står vinkelrett på hverandre og har et felles skjæringspunkt, origo O. Betegnelsene for koordinatplanene velges slik at xy-planet inneholder x-aksen og y-aksen og står vinkelrett på z-aksen, og tilsvarende for de andre to planene. Homogene koordinater kan også defineres i rommet.

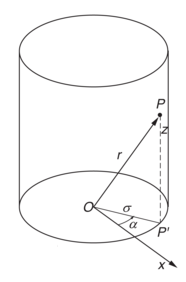
Nær beslektet med de rettvinklede koordinatene er sylinderkoordinater. Her bestemmes punktet P ved sin høyde z over xy-planet, lengden σ = OPʹ av radius' vektors (r = OP) projeksjon på xy-planet og vinkelen α som OP' danner med x-aksen.

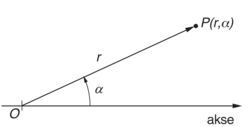
Polarkoordinater i rommet kalles også kulekoordinater eller sfæriske koordinater. Her bruker man radius vektor r, vinkelen α og den vinkelen β som radius vektor danner med xy-planet til å bestemme P. Disse vinklene svarer til lengde og bredde på en globus.

Koordinatbegrepet kan utvides til flerdimensjonale rom, og omvendt er koordinatsystemet den enkleste måten å definere rom i høyere dimensjoner enn tre. Man kan også generalisere koordinatbegrepet til å bestemme andre geometriske størrelser enn punkter.

Det var den franske matematikeren og filosofen René Descartes som innførte koodrinatsystemene. Det finnes imidlertid tilløp til koordinatgeometri hos tidligere forfattere, og Pierre de Fermat viste tydelig i et brev til Gilles Personne de Roberval (1629) at han behersket metoden, til og med i en form som svarer nærmere til den som blir brukt nå.

Gjennom analytisk geometri skapes et bindeledd mellom geometri og algebra som er av fundamental betydning for utviklingen av infinitesimalregningen og den moderne matematikk i det hele tatt.

• geometri
• matematikk